在棉花分级过程中,棉花回潮率会严重影响断裂比强度等品质指标检测结果[1-4],因此,棉花分级检测通常在温度(20±2)℃和相对湿度(65±3)%的标准大气条件下进行测试[5]。在品质指标测试前,必须让棉花与环境达到平衡状态,使棉纤维回潮率在一定范围内。因为控制测试环境固有成本高和技术困难,促使学者探索非标准检测环境下的检测路径,且棉纤维断裂比强度等指标随着回潮率的变化而变化,可建立回潮率修正模型[6],但该路径的核心前提是回潮率的实时精确测量。
目前,测量棉纤维回潮率的方法分为直接法和间接法,直接方法例如烘干法,检测准确率高,但耗时且效率低。间接方法通常使用电阻、电容、微波、近红外等检测方法[7-9],具备高速性与可持续性。其中,电阻式传感具有快速、准确和成本效益等优势,文献[10-11]采用电阻法设计研发了加工过程中籽棉回潮率在线检测装置,陕西华斯特仪器有限责任公司设计了一种便携式棉花回潮率测定仪,该仪器将棉样放在两个电极板之间,通过电极板挤压棉样,结合压力测量棉花的回潮率[12]。然而,现有的设备多针对松散棉团设计,为消除棉纤维密度的影响,通常采用固定密度或者压力补偿的方法测量。FANG等[13]针对棉花收获时,籽棉密度不一致影响回潮率测量的问题,根据电级压力与密度之间的关系,提出压力补偿的籽棉回潮率检测方法。而在棉花品质指标检测过程中,棉纤维通常会被梳理成束状,形态的改变使影响电导率的因素发生变化,进而对基于电特性的检测方法产生不利影响。
本研究聚焦棉花束纤维这一特殊形态,提出基于电阻法的回潮率实时检测方法。搭建电阻-图像同步采集平台,通过图像特征表征棉层厚度,探究电极间距与棉层厚度对电阻测量值的耦合作用机制;确定最佳的棉花束纤维回潮率检测方案,构建适应束状纤维的回潮率预测模型。
本实验棉花样本取自新疆生产建设兵团第十二师二二二团某棉花加工企业,品种为新陆早80号,其品质为:衣分率43.0%,纤维上半部平均长度30.0 mm,断裂比强度31.4 cN/tex,马克隆值4.7,整齐度指数85.3%。
实验所用的仪器主要有棉纤维电阻测量模块与棉纤维图像采集系统,如图1所示。棉纤维电阻测量模块集成精密机械传动与电子传感单元:夹持机构采用气动-伺服混合驱动设计,通过气缸施加0.3 MPa恒定压力夹持固定纤维束,伺服电机控制横向位移实现电极间距精准调节;电阻测量单元电路板为实验室研制,其精度如表1所示。图像采集系统由CCD相机(相机型号为SV-H600C-C,镜头型号为SV-0814-H)、LED面光源及棉纤维吸风口组成,在进行图像采集时,棉纤维被吸入吸风口双层高透明光学玻璃之间,使纤维保持伸直状态,通过工业相机拍摄棉纤维图像。
表1 电阻测量电路板精度
Tab.1 Circuit board accuracy of resistance measurement

标准电阻/MΩ1101001000200010000测量均值/MΩ1.039.81106.11028.62102.69717.1标准差/MΩ0.0110.0060.06611.75615.23651.407相对偏差/%2.51.96.12.95.12.8
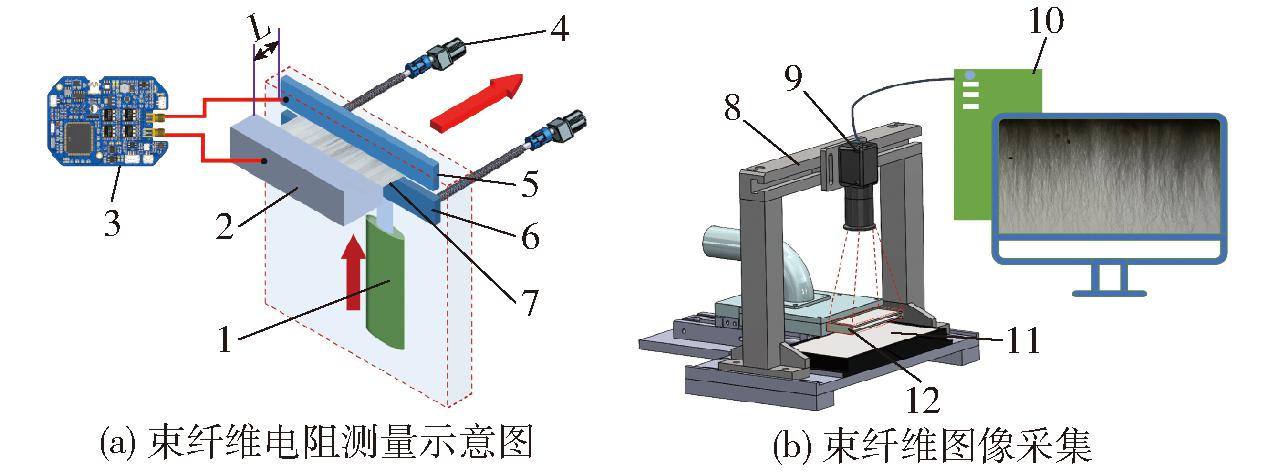
图1 实验装置示意图
Fig.1 Schematics of experimental setup
1.气缸 2.纤维取样器 3.电阻测量电路板 4.伺服电机 5.纤维夹持钳口上鄂(固定) 6.纤维夹持下颚 7.束纤维 8.相机支架 9.CCD相机 10.计算机 11.光源 12.棉纤维吸风口
其他仪器设备有:恒温恒湿箱(FQY/WSK-400C型,广州市丰千源环境试验设备有限公司,温度偏差±2℃,相对湿度偏差±3%),用于制作不同回潮率棉样;半自动通风式快速恒温烘箱(YG767型,南通三思机电科技有限公司,控温精度±1℃),用于测量棉纤维的实际回潮率;电子天平(XY500C型,常州市幸运电子设备有限公司,精度±0.01 g),用于称量棉样。
本研究的对象为自动制样机构梳理后形成的锥型束状棉纤维,距离纤维夹持器越远,棉层厚度越小。沿着束纤维夹持边缘逐行提取图像R、G、B通道及灰度均值,如图2所示,随着与纤维夹持根部距离的增加,R、G、B值及灰度均值均呈递增趋势。根据Lambert-Beer定律[14],材料吸光度与吸收层厚度成正比,纤维材料厚度与透过材料光强呈负相关,随着棉层厚度变小,透过纤维光强会增大,进而导致R、G、B值及灰度特征增大。
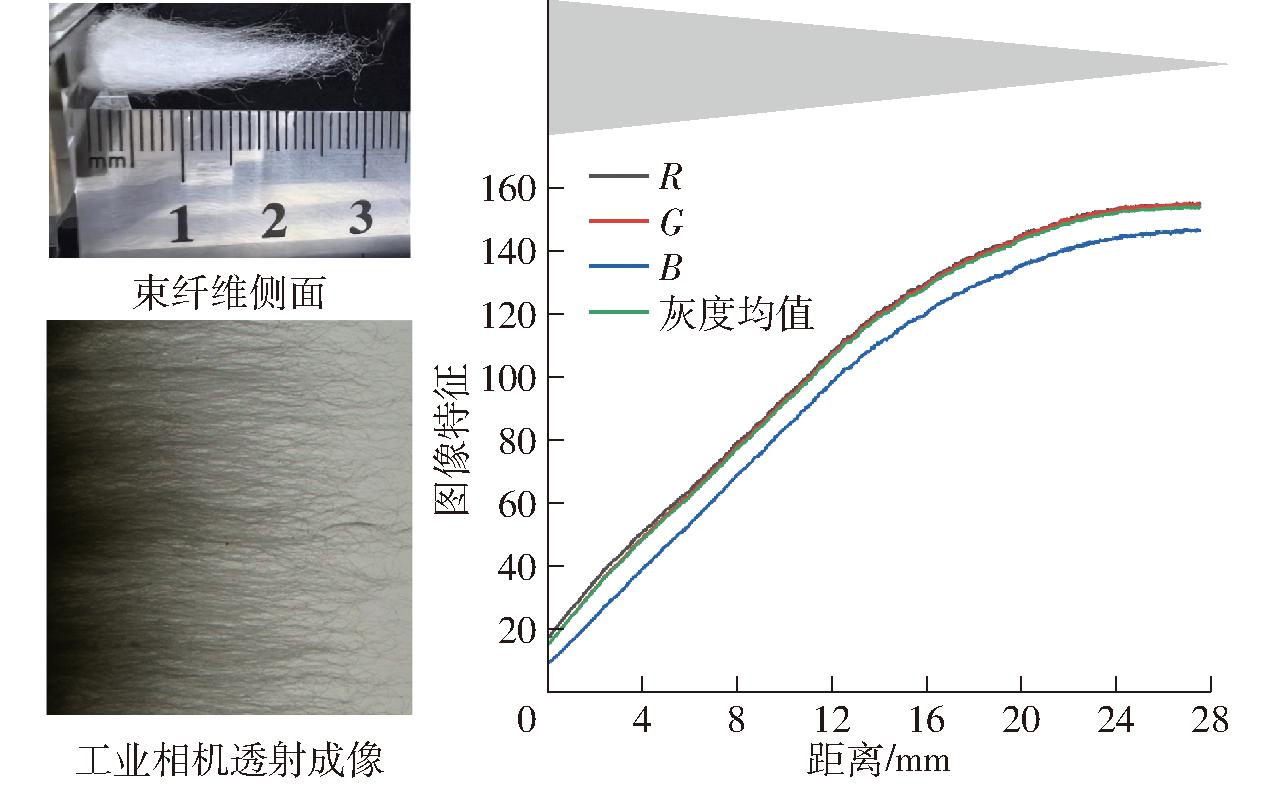
图2 棉纤维的形态与图像特征随距离变化曲线
Fig.2 Relationship between morphology of cotton fibers and image features with distance
在测量材料电阻时,可将两电极之间的被测对象当作导体,棉纤维内部的水分使其具有导电性,对于一个导体,其电阻测量公式为
(1)
式中 R——材料电阻,Ω
ρ——材料电阻率,Ω·m
L——材料长度,m
S——材料面积,m2
根据公式(1),对于棉花束纤维,电极之间纤维长度与厚度会影响电阻测量,纤维回潮率与温度会影响纤维电阻率,因此,本研究棉花束纤维回潮率检测方法主要包括4个步骤:获取电阻与图像信息;探究电阻测量影响因素;提出回潮率测量方案;建立回潮率预测模型(图3)。
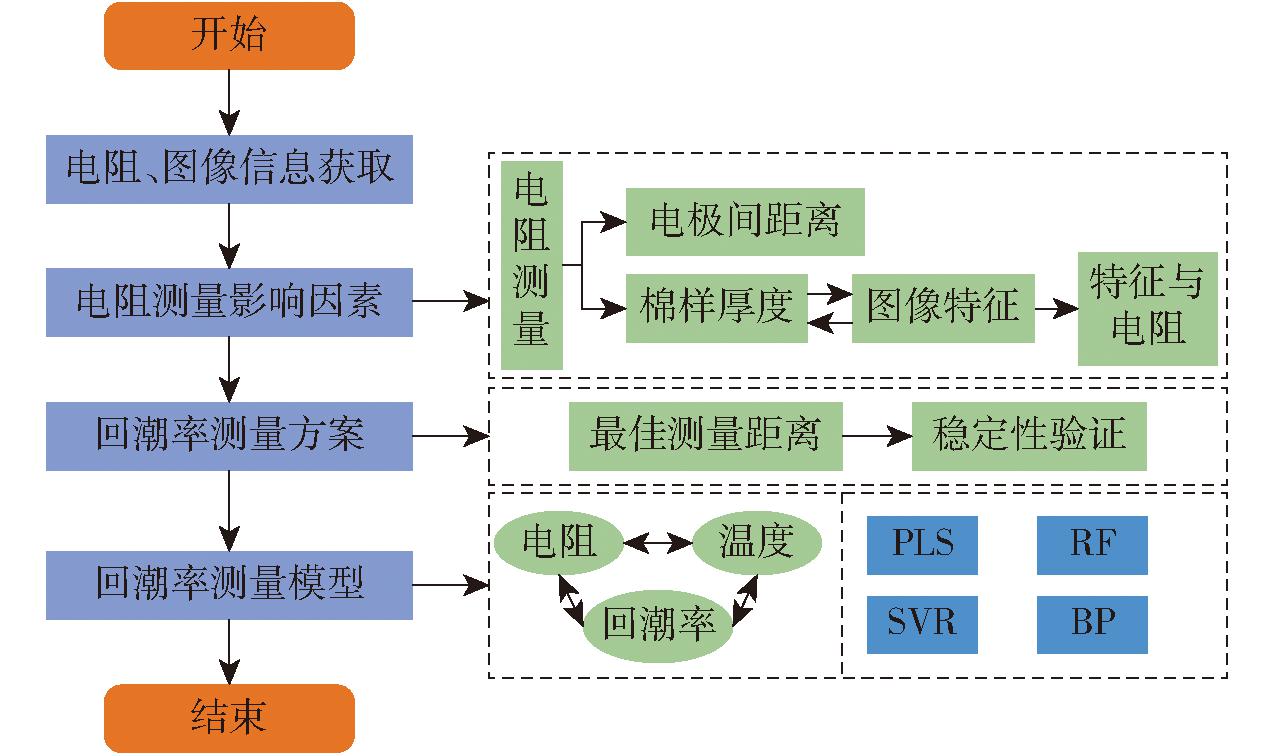
图3 棉花束纤维回潮率检测技术路线图
Fig.3 Technical route for detecting moisture regain rate of cotton bunch fibers
1.3.1 数据获取路径
本实验数据获取流程如图4所示。环境温湿度变化会影响其含水率[15-16],并结合棉花收购回潮率低于12%的要求,为获取不同回潮率的棉样,分别在温度10、15、20、25、30℃,相对湿度30%、40%、50%、60%、70%、80%梯度的恒温恒湿箱环境中吸湿平衡处理24 h后,每组取100 g棉样,分别进行以下处理:①取50 g棉样经由实验平台[17]自动制备成束纤维,并进行电阻测量与纤维图像采集。②将剩余50 g棉样放入八篮烘箱依据公式[18]获得真实回潮率。
(2)
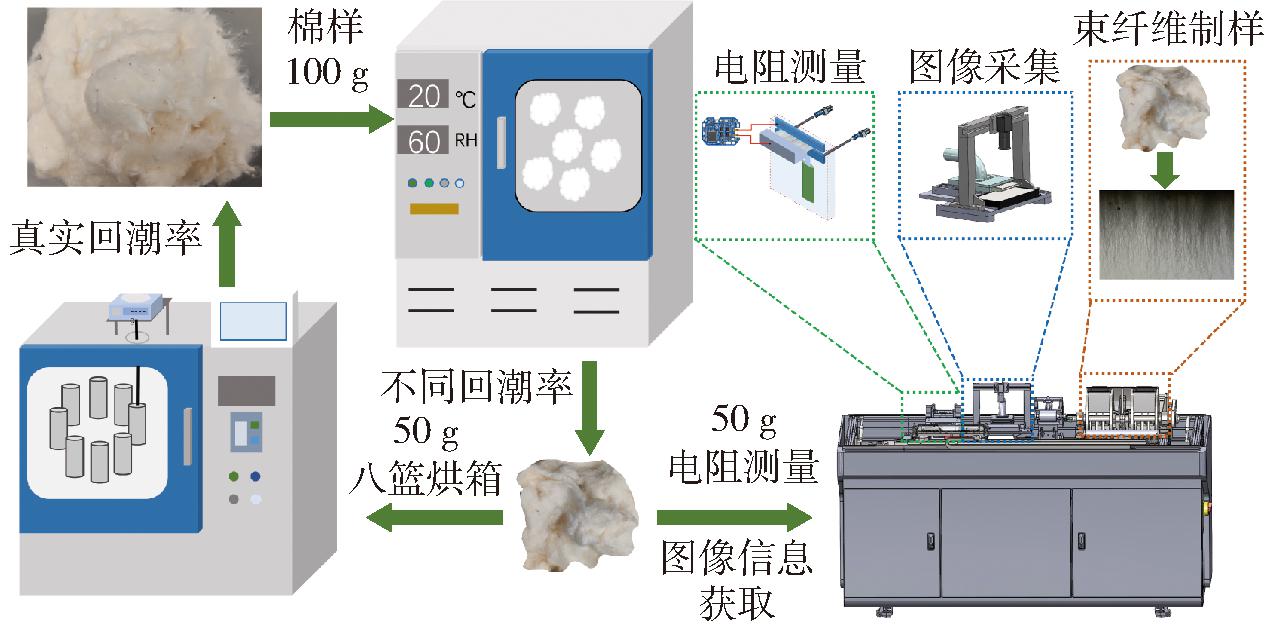
图4 数据获取流程图
Fig.4 Data acquisition process
式中 MR——棉纤维回潮率,%
m——烘干前质量,g
m0——烘干后质量,g
如表2所示,培养棉花样本回潮率范围为3.94%~12.2%,共32个回潮率等级。
表2 不同培养环境温湿度时测量回潮率
Tab.2 Moisture regain measured at different temperatures and humidity of culture environment %
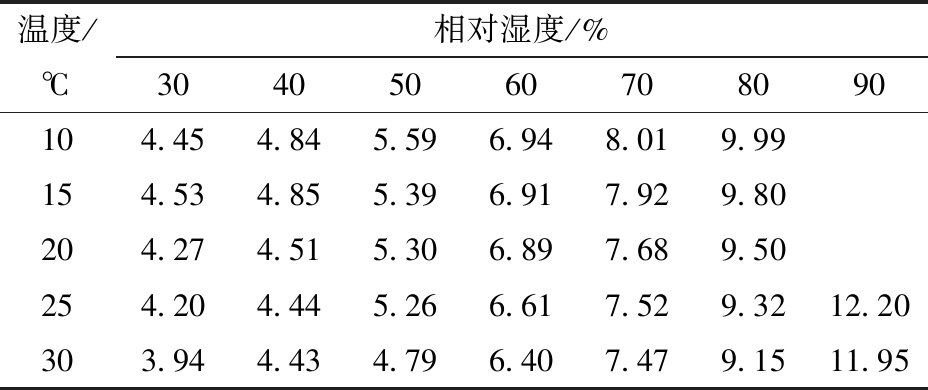
温度/℃相对湿度/%30405060708090104.454.845.596.948.019.99154.534.855.396.917.929.80204.274.515.306.897.689.50254.204.445.266.617.529.3212.20303.944.434.796.407.479.1511.95
1.3.2 电阻测量与图像特征获取
为探究电极间距对电阻测量的影响规律,随机选取同一温度下,涵盖低、中、高回潮率的样本开展实验,选取25℃条件下制备的4.44%、6.61%、12.2%回潮率棉样。对于每个棉样,分别在距离纤维夹持器2、4、6、8、10、12 mm 6个电极间距处进行电阻采集(图5,图中R0为纤维夹持装置电阻,RB~RF为每2 mm距离纤维的区段电阻),每个回潮率完成6组平行试样×6间距点位测试,共36组电阻数据。
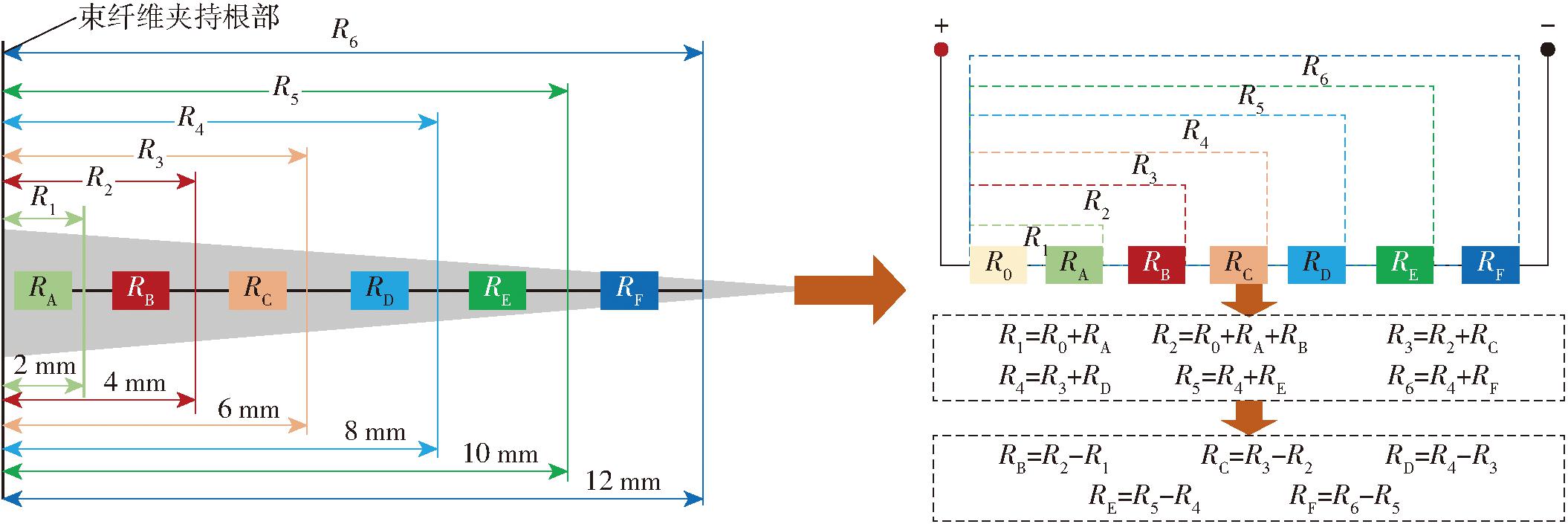
图5 棉纤维电阻串联示意图
Fig.5 Schematic of cotton fiber resistance equivalent series connection
测量电阻过程中,随着电极间距的增大,沿着纤维束末端方向,棉层厚度也在变薄。为讨论棉层厚度对棉花束纤维电阻测量的影响规律,每次测量电阻后采集棉纤维图像。为消除电极间距对电阻测量的干扰,依据串联电阻模型理论,如图5将0~12 mm的纤维划分为6个电阻区段(RA、RB、RC、RD、RE、RF),通过差分计算各段电阻,其中RA因受夹持器接触阻抗干扰予以剔除,最终获取RB、RC、RD、RE、RF共5个区段电阻。通过数字图像处理对纤维图像从2 mm处开始以2 mm等间距分割,得到每个区段纤维所对应图像,共获得30组区段纤维电阻数据及30组对应图像。
分别提取上述图像的R、G、B 3个颜色通道的一阶颜色矩以及灰度均值图像特征,共4维颜色特征[19]。一阶颜色矩采用一阶原点矩,即均值,反映图像整体明暗程度,值越大,图像越亮。
(3)
式中 Em——所有像素第m个颜色通道的颜色均值
Pmn——第n个像素在第m个颜色通道上的颜色值
N——图像总像素数
图像灰度均值是指图像中所有像素灰度算术平均值,它反映了图像整体亮度水平,通过累加图像中所有像素的灰度,然后除以像素总数来计算平均灰度
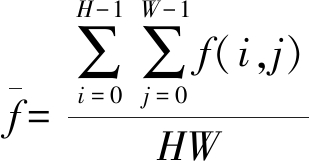
(4)
式中 f(i,j)——图像中第i行、第j列像素灰度
H——图像高度
W——图像宽度
1.3.3 回潮率预测模型
本研究通过构建机器学习模型[20]实现棉纤维回潮率预测。按照图4所示数据获取流程得到表2的32个不同回潮率水平的棉花样本,每个回潮率下测试6份束纤维,并采集距离纤维夹持器2 mm处的电阻,总共获得192(32×6)组电阻数据。
模型是基于Python 3.7语言和Jupyter Notebook编辑器构建,选择温度与电阻作为预测回潮率的特征变量,将数据归一化处理。数据集按照比例7∶3随机划分为训练集与测试集,比较了4个机器学习算法:偏最小二乘回归(Partial least squares regression, PLSR)[21]、随机森林(Random forest, RF)[22]、支持向量回归(Support vector regression, SVR)[23]和反向传播神经网络(Back propagation neural network, BPNN)[24]。模型评估采用均方根误差(Root mean square error, RMSE)表征预测偏差程度,平均绝对误差(Mean absolute error, MAE)反映预测稳定性,决定系数(Coefficient of determination, R2)评估模型解释能力。通过对比分析各模型在测试集上的表现,筛选最优回潮率预测模型。
如图6所示,在25℃条件下测试回潮率4.44%、6.6%、12.2%棉花束纤维的电阻特性,纤维电阻与电极间距呈显著正相关,在3个回潮率中呈现一致规律。电阻测量随着电极间距离增大,同回潮率下样本间电阻误差也增大。
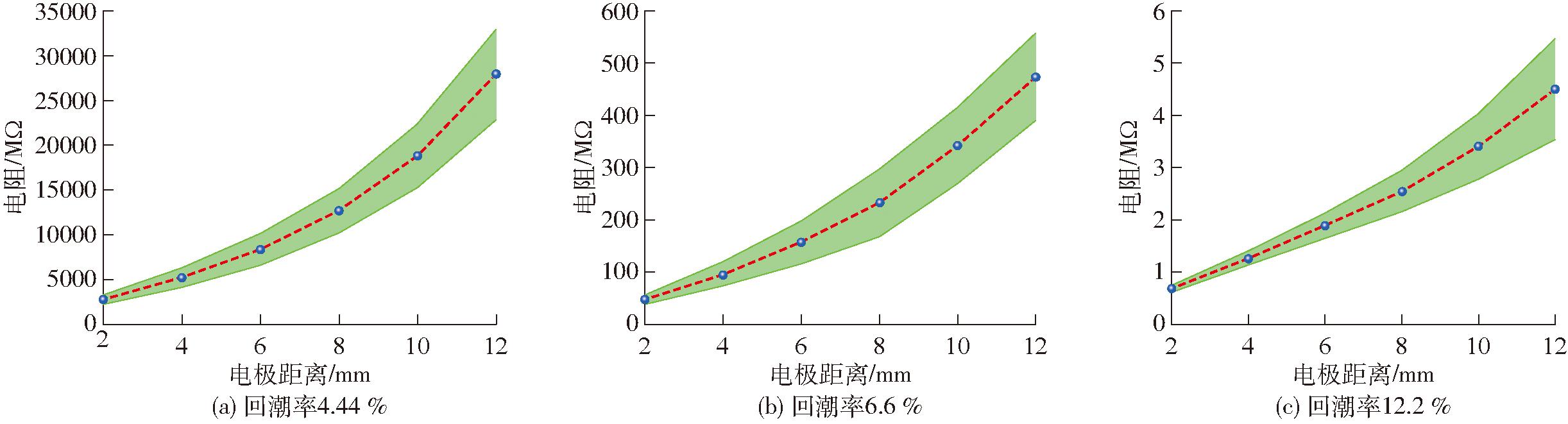
图6 不同纤维样本电阻测量误差分析 Fig.6 Resistance measurement error analysis of different fiber samples
如图7所示,在回潮率4.44%、6.6%、12.2%下,纤维区段B、C、D、E、F的电阻均呈递增趋势。
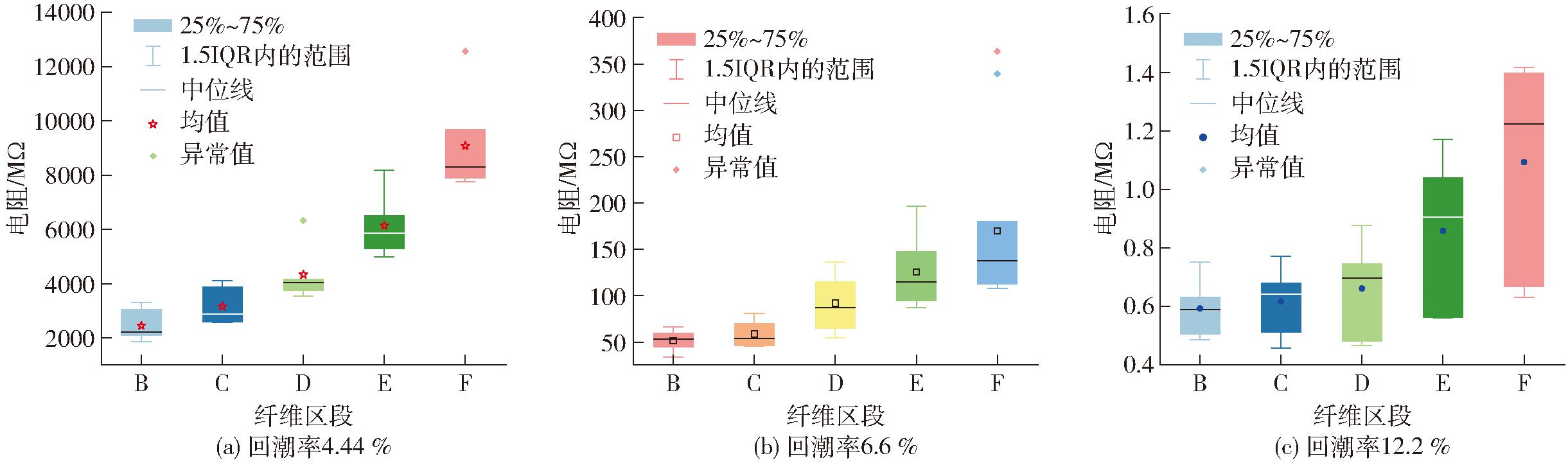
图7 等效串联后每2 mm电阻变化
Fig.7 Resistance changes every 2 mm after equivalent series connection
对提取的图像特征与纤维电阻采用Spearman相关性分析,如表3所示,RGB颜色通道的一阶颜色矩以及灰度均值4个特征与电阻表现出较强相关性,其中在回潮率4.44%时,RGB通道的一阶颜色矩以及灰度特征与电阻相关系数为0.96。在回潮率升高时,RGB通道的一阶颜色矩及灰度特征与电阻相关系数降低。
表3 不同回潮率下电阻与图像特征的Spearman相关系数
Tab.3 Spearman correlation coefficient between resistance and image features at different moisture regain rates

图像特征参数回潮率/%4.446.612.2灰度均值0.960.830.77R通道一阶颜色矩0.960.830.77G通道一阶颜色矩0.960.830.77B通道一阶颜色矩0.960.840.77
根据表3,在回潮率4.4%、6.6%、12.2%下,灰度均值以及RGB颜色通道的一阶颜色矩与测量电阻的Spearman相关系数无较大差异,本研究选用灰度图像特征与测量电阻做回归分析,如图8所示。结果表明,在3个回潮率下,纤维的灰度图像特征与电阻之间存在非线性关系,随着灰度均值的增大,电阻呈非线性上升,拟合曲线R2分别达到0.92、0.70、0.81,这是因为随着棉层厚度变小,灰度特征变大,对于束纤维这一导体,根据公式(1),当其厚度变薄后,减小了纤维材料导电截面积,导致电阻增大。
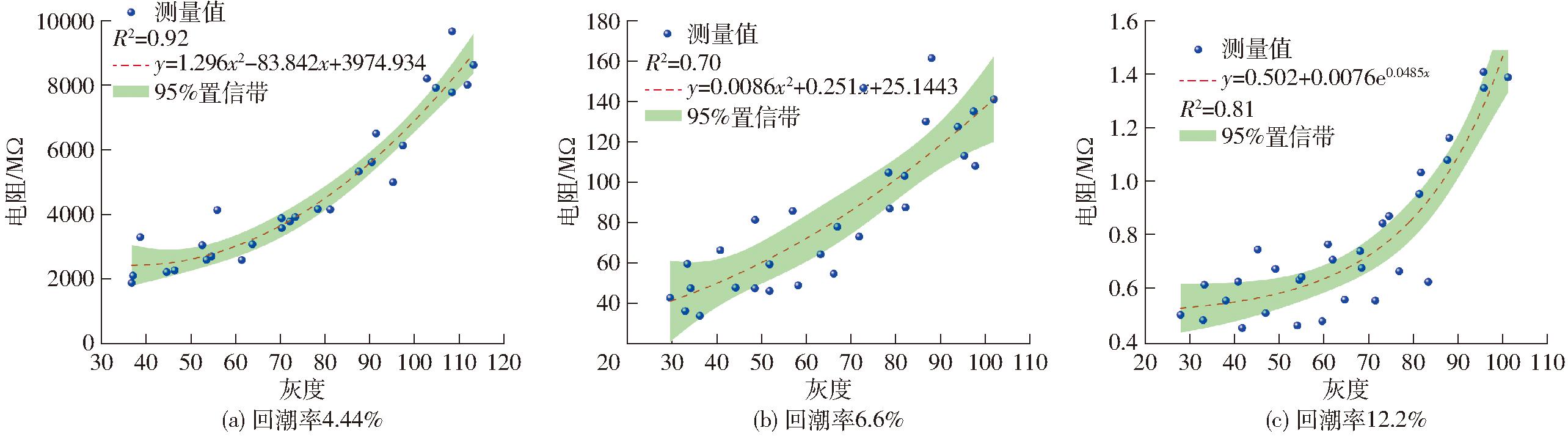
图8 灰度图像特征与电阻关系曲线
Fig.8 Grayscale image features vs resistance curves
前期实验结果表明,棉纤维图像灰度特征与电阻之间存在非线性关系。通过分析3个回潮率下6个样本在2、4、6、8、10、12 mm时纤维图像灰度特征的变化以及误差发现,灰度特征随距离的增加呈上升趋势(图9),但其误差基本趋于稳定,这表明对于不同的纤维样本,距离的增加对于棉层厚度变化的差异影响有限,然而,从图6观察到电阻测量误差随电极间距变大而显著增加。如图10所示,以回潮率4.44%纤维灰度特征与电阻关系曲线为例,在相等灰度差值情况下,高灰度区电阻波动幅度显著高于低灰度区,解释了电极间距增大导致电阻测量误差扩大的内在机制,即棉层厚度减小会显著增大电阻测量误差。基于此,本研究选择2 mm电极间距作为最优检测参数,以最大限度降低电阻测量系统误差,为后续回潮率预测模型构建提供准确数据。
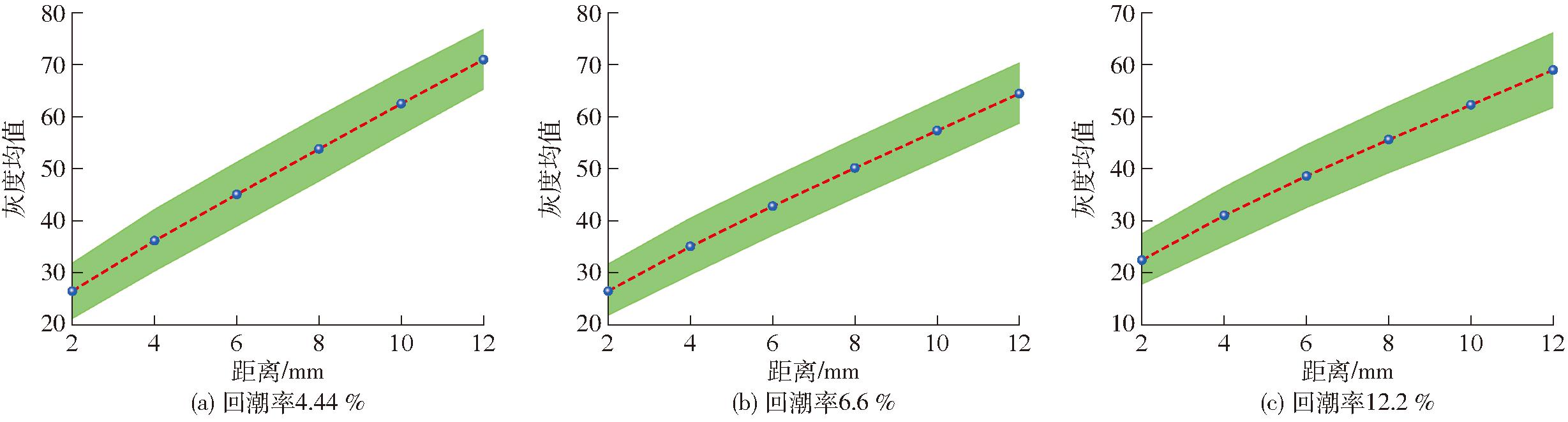
图9 不同距离下灰度图像特征随距离变化误差分析
Fig.9 Analysis of error of grayscale image features with distance at different distances
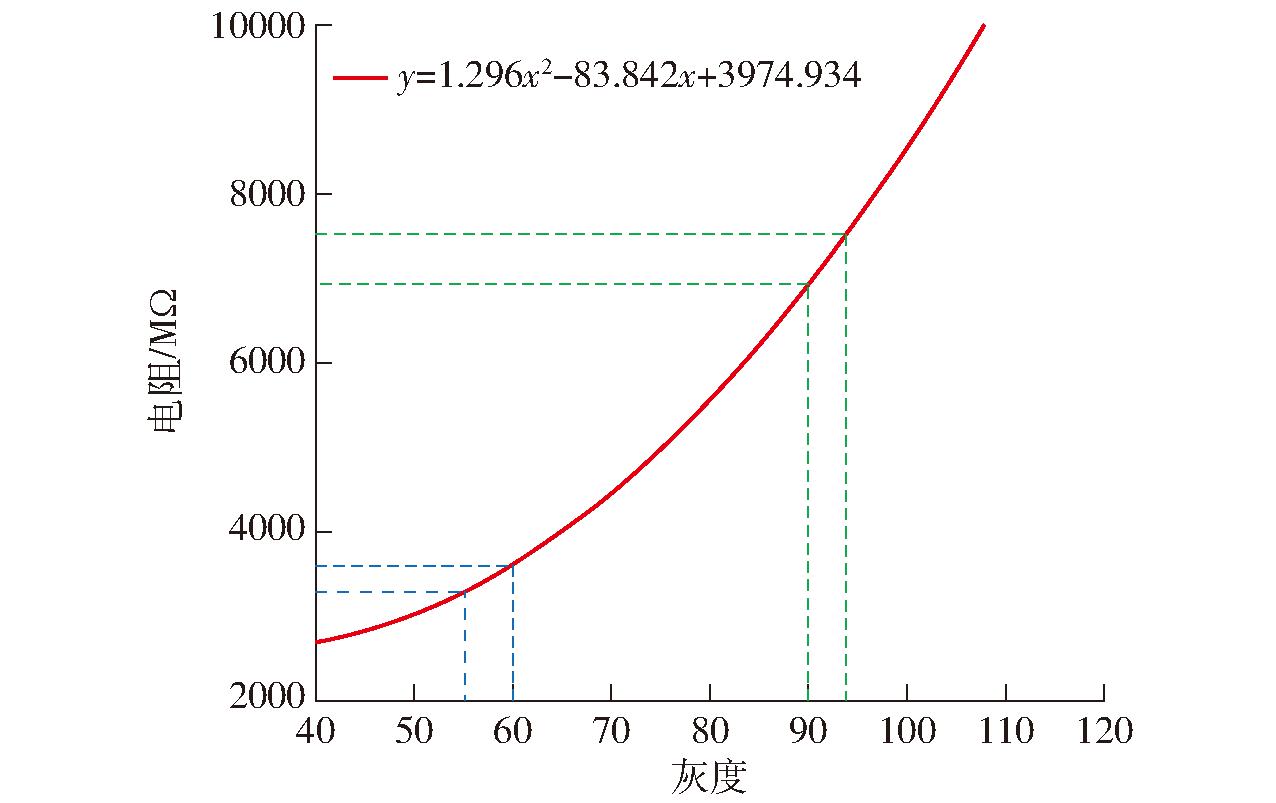
图10 不同灰度(厚度)电阻测量误差分析
Fig.10 Analysis of measurement errors with different gray (thickness) resistances
由于棉纤维长度等品质会影响棉花束纤维形态,为确保在2 mm处测量电阻不受棉花品质的影响,选用8个不同品质的棉花样本,如表4所示,分别在2 mm处测量电阻,并验证测量电阻的稳定性。
表4 不同等级纤维品质指标
Tab.4 Fiber quality indicators of different grades
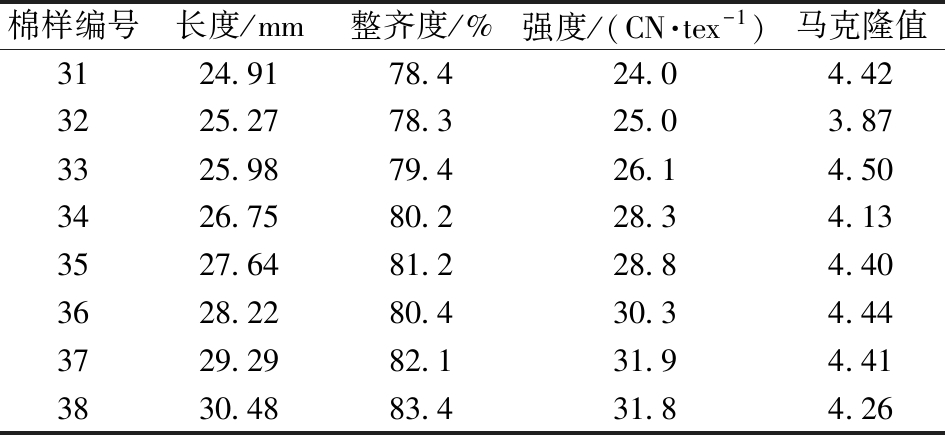
棉样编号长度/mm整齐度/%强度/(CN·tex-1)马克隆值3124.9178.424.04.423225.2778.325.03.873325.9879.426.14.503426.7580.228.34.133527.6481.228.84.403628.2280.430.34.443729.2982.131.94.413830.4883.431.84.26
采用质量控制图评价2 mm处纤维电阻测量的稳定性,绘制了均值极差图(X-R图)[25-26],如图11所示,上控制限(Upper control line,UCL)、下控制限(Lower control line,LCL)则是在均值基础上加减3个标准偏差(Standard deviation,S)。分析结果显示,各组测量电阻均在上下控制限之内,具有较好的稳定性。同时对各组数据进行单因素方差分析,如表5所示,在同一环境下8个不同品质的棉样各组之间电阻测量无显著性差异(P>0.05),在2 mm处测量电阻时,纤维电阻不受棉花品质的影响。
表5 同一温湿度环境下不同等级纤维电阻测量组间单因素方差分析
Tab.5 One-way analysis of variance between different levels of fiber resistance measurement groups under the same temperature and humidity environment

来源自由度平方和均方FP组间71641188.60234455.512.0480.079组内323663225.69总计395304414.30
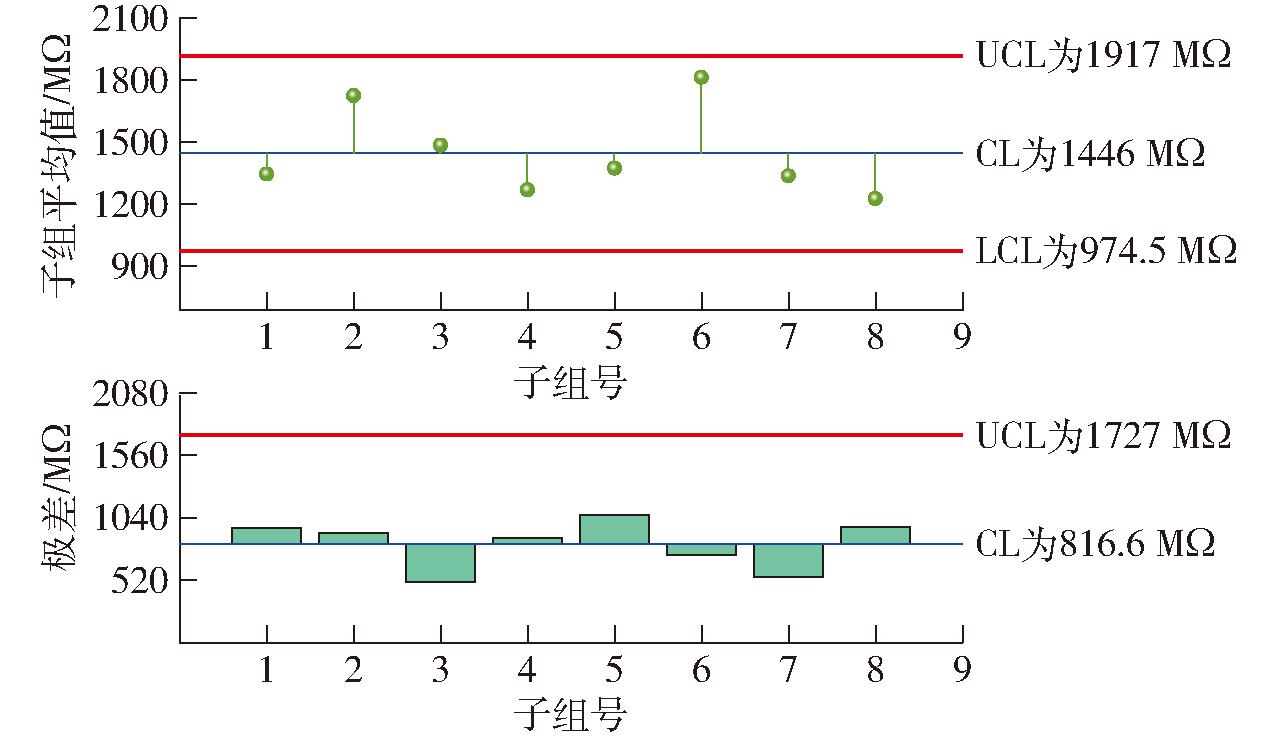
图11 不同品质纤维在2 mm处电阻测量控制图
Fig.11 Control diagram of resistance measurement at 2 mm for different quality fibers
基于32个不同水平回潮率192份纤维样本的温度、电阻、回潮率数据,Spearman相关分析表明,电阻与回潮率相关系数高达-0.94,温度与电阻呈负相关(-0.22),主要原因为随着温度的升高,增强了电子的热运动,增加了导电性,导致电阻降低。
为研究电阻与回潮率之间的关系,在30℃条件下,建立电阻与回潮率的非线性关系,如图12所示,R2达到0.98,从图中可以很明显地看到,电阻在回潮率4%~6%快速下降,之后下降趋势逐渐变缓,主要原因是随着棉纤维中水分增加,其导电能力也增加,致使电阻降低。
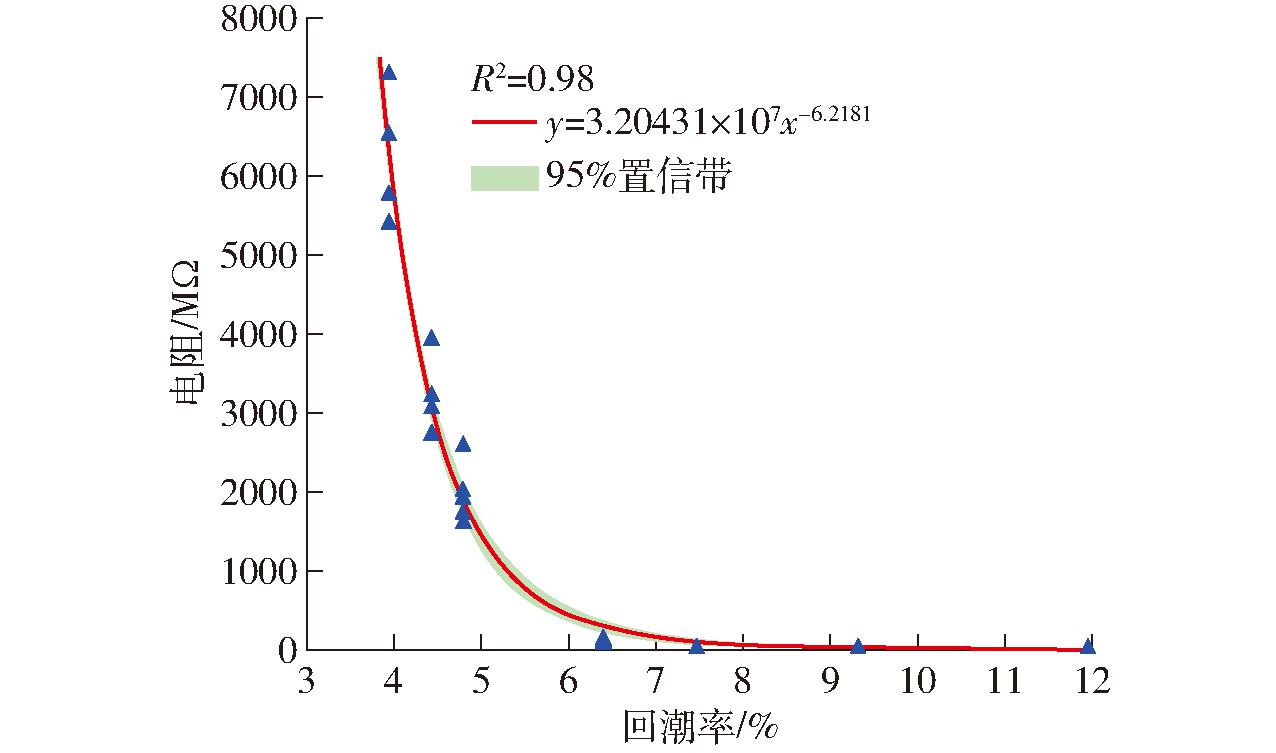
图12 30℃下电阻与回潮率拟合回归曲线
Fig.12 Fitted regression curve of resistance versus moisture regain at 30℃
选择温度和电阻作为回潮率预测模型的特征,以八篮烘箱所测回潮率为真实值,选用偏最小二乘、随机森林、支持向量机、BP神经网络4种算法建模,在测试集上评估每个模型的预测准确性。如表6所示,随机森林模型预测效果最佳,R2为0.99,RMSE为0.24%,MAE为0.14%,表明随机森林模型对于束纤维回潮率预测具有较好的稳定性与准确性。
表6 不同预测模型性能评估指标比较
Tab.6 Comparison of performance evaluation metrics of different predictive models
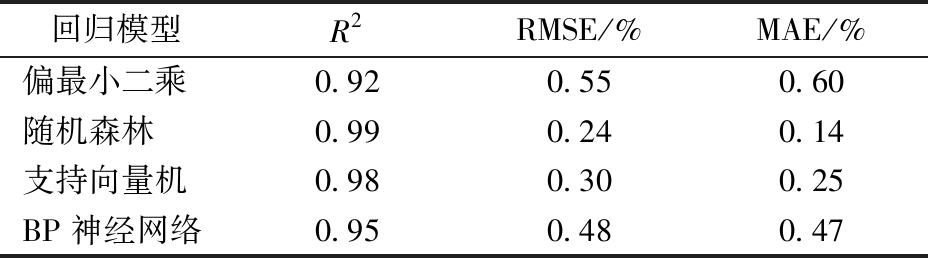
回归模型R2RMSE/%MAE/%偏最小二乘0.920.550.60随机森林0.990.240.14支持向量机0.980.300.25BP神经网络0.950.480.47
为了验证回潮率预测模型的可靠性,制备了7组不同回潮率的棉花样本进行实验验证,如图13和表7所示,每组样本分为2组,一组使用八篮烘箱测量回潮率真实值,另一组使用实验平台对同一样本测量6次,预测结果表明,6次预测均值与真实值拟合曲线关系为y=1.013x,R2为0.99,平均绝对误差0.24%,均方根误差0.26%,表明本研究建立的棉纤维回潮率预测方法及模型具有较高的可靠性与准确性。
表7 RF模型回潮率预测结果
Tab.7 RF model moisture regain prediction results %

组别回潮率真实值模型预测结果123456均值标准差平均绝对误差均方根误差14.754.795.264.674.734.734.794.830.220.120.2125.245.025.015.015.015.014.844.980.070.260.2637.387.687.687.757.827.557.537.670.110.310.2948.508.808.808.278.728.788.858.700.220.280.2959.309.099.189.169.199.169.219.170.040.140.14610.3010.4310.0610.0510.0510.049.8310.080.190.270.29711.6411.9211.9611.9611.9611.9611.8911.940.030.300.30
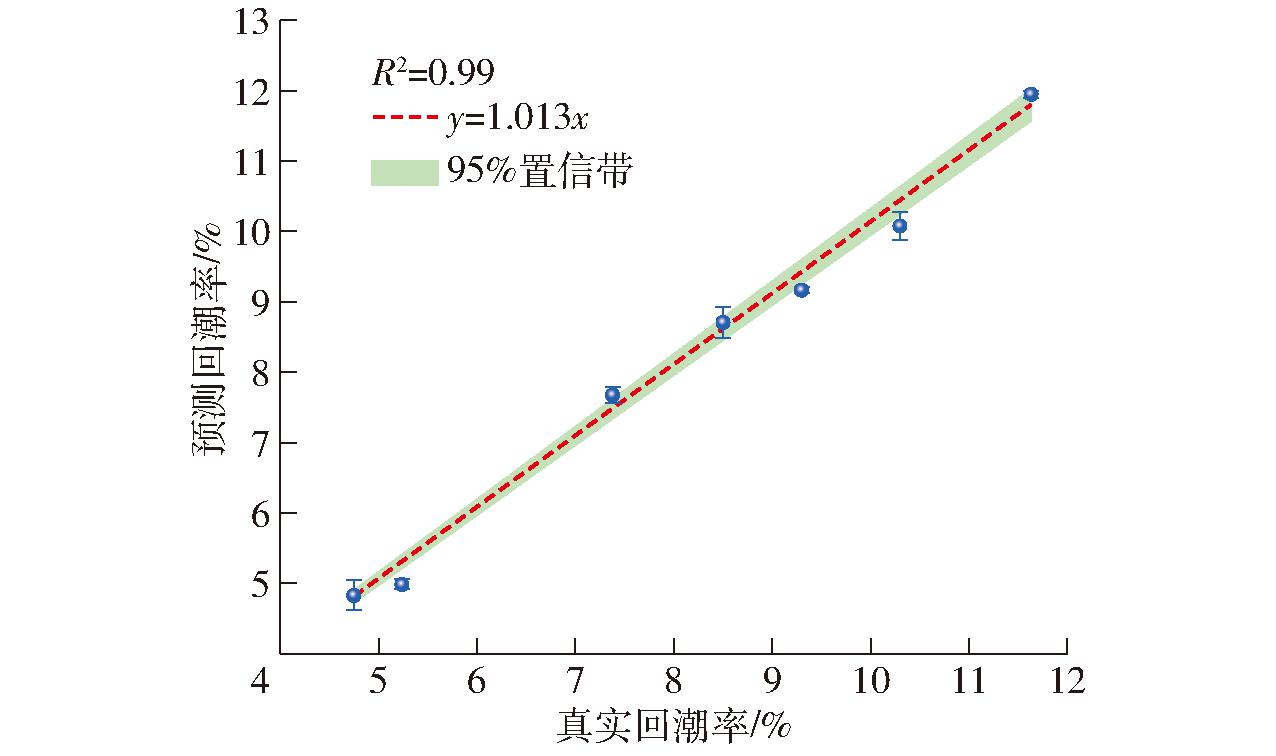
图13 RF模型预测值与真实值拟合曲线
Fig.13 RF model predicted value fitted to true value
(1)电极间距离与棉层厚度对电阻测量具有耦合效应。电阻值测量与电极间距呈正相关;采用棉纤维图像特征表征厚度,棉纤维灰度图像特征与电阻具有较高的相关性,且棉纤维电阻与灰度特征呈非线性关系,回潮率4.44%、6.6%、12.2%下,电阻与灰度拟合函数R2分别为0.92、0.7、0.81。
(2)棉花束纤维回潮率检测最优参数选择与普适性验证。棉层厚度减小会显著增大电阻测量误差,据此提出2 mm电极间距为最优检测参数,且在该参数下不同品质棉花束纤维电阻无显著差异(P>0.05),验证了该方法对纤维异质性的鲁棒性。
(3)回潮率检测模型构建与验证。电阻与温度(Spearman系数为-0.22)、回潮率(Spearman系数为-0.94)均呈负相关,基于随机森林(RF)算法构建的电阻-温度双变量预测模型性能最优(测试集:R2=0.99,RMSE为0.24%;独立验证集:R2=0.99,RMSE为0.26%),验证数据标准差为0.03%~0.22%,结果表明模型具有较好的稳定性。
本研究提出的电阻法突破了传统松散棉团状纤维回潮率检测的局限性,实现了束状纤维形态下的回潮率快速测量,为断裂比强度等指标的动态补偿提供了可靠数据基础。所揭示的电极间距-厚度-电阻关联机制,可为其他纤维类物料回潮率传感技术开发提供理论支撑。
[1] 于慈春,于照乾.回潮率对棉纤维品质的影响[J].中国纤检,2006(11):51-53.
YU Cichun,YU Zhaoqian.The influence of moisture regain on the quality of cotton fibers[J].China Fiber Inspection,2006(11):51-53.(in Chinese)
[2] 莫靖昱,胡秦萍,眭建华.回潮率对棉纤维物理性状影响的探讨[J].苏州大学学报,2010,30(1):24-27.
MO Jingyu, HU Qinping, SUI Jianhua. Study on the effect of moisture regain on physical properties of cotton fibers[J]. Journal of Soochow University, 2010, 30(1): 24-27.(in Chinese)
[3] 史书伟,向天明,刘伟刚,等.棉花加工过程中回潮率对皮棉质量的影响[J].棉纺织技术,2020,48(8):19-23.
SHI Shuwei, XIANG Tianming, LIU Weigang, et al. Influence of moisture regain on ginned cotton quality in cotton processing[J]. Cotton Textile Technology, 2020, 48(8): 19-23.(in Chinese)
[4] DELHOM C D, KELLY B, MARTIN V. Cotton fiber: physics, chemistry and biology[M]. Cham: Springer International Publishing, 2018.
[5] 中华全国供销合作总社. GH/T 1304—2020:籽棉回潮率微波测量仪[S]. 北京:中国标准出版社,2020.
[6] KNOWLTON J L. Effect of moisture on cotton fiber strength[C]∥Proceedings of the Beltwide Cotton Conference,1996:1300-1305.
[7] 许明翥,葛陈勇,方文娟,等.微波法籽棉回潮率测试仪在籽棉收购加工中的应用研究[J].分析仪器,2020(2):97-103.
XU Mingzhu, GE Chenyong, FANG Wenjuan, et al. Research on application of microwave seed cotton moisture regain tester in seed cotton scquisition and processing[J]. Analytical Instrument, 2020(2): 97-103.(in Chinese)
[8] 陈亚军,杨舒涵,史书伟,等.基于近红外法的棉花回潮率测量系统研制与试验[J].农业工程学报,2021,37(7):158-165.
CHEN Yajun, YANG Shuhan, SHI Shuwei, et al. Development and experiments of cotton moisture regain measurement using near-infrared method[J]. Transactions of the CSAE, 2021, 37(7): 158-165.(in Chinese)
[9] 王梦,李成松,坎杂,等.棉花回潮率测量方法发展现状[J].江苏农业科学,2014,42(3):268-270.
WANG Meng, LI Chengsong, KAN Za, et al. Development status of cotton moisture regain measurement methods[J]. Jiangsu Agricultural Sciences, 2014, 42(3): 268-270.(in Chinese)
[10] 杨海军,李顺利,张霖.籽棉回潮率在线检测技术研究[J].中国棉花加工,2009(6):40-42.
YANG Haijun, LI Shunli, ZHANG Lin. Research on on-line detection technology of seed cotton moisture regain[J]. China Cotton Processing, 2009(6): 40-42.(in Chinese)
[11] 桑小田.基于质量比电阻的籽棉回潮率在线检测系统设计[D].郑州:郑州大学,2016.
SANG Xiaotian.Design of seed cotton moisture on-line detecting system based on mass specific resistance[D]. Zhengzhou:Zhengzhou University, 2016.(in Chinese)
[12] 司文奎,金利,杜东峰,等.一种便携式棉花回潮率测定仪:CN202120237518.2[P].2021-09-28.
[13] FANG L, ZHANG R, DUAN H, et al. Resistive sensing of seed cotton moisture regain based on pressure compensation[J]. Sensors, 2023, 23(20): 8421.
[14] 吴美琴,王府梅. 纤维层面密度的光学新算法[J].东华大学学报(自然科学版), 2016, 42(6): 827-834.
WU Meiqin, WANG Fumei. A new optical algorithm for calculating the area density of fiber layers[J].Journal of Donghua University (Natural Science Edition), 2016, 42(6): 827-834.(in Chinese)
[15] 陈莉,黄故,刘中君.彩色棉纤维吸湿性能研究[J].棉纺织技术,2005(11):33-35.
CHEN Li, HUANG Gu, LIU Zhongjun. Research on moisture absorption property of colored cotton fiber[J].Cotton Textile Technology, 2005(11): 33-35.(in Chinese)
[16] 周锦芳.棉纤维的结构与性质[J].中国纤检,1983(3):19-26.
ZHOU Jinfang. Structure and properties of cotton fibers[J].China Fiber Inspection, 1983(3): 19-26.(in Chinese)
[17] 张若宇, 韩晨阳, 常金强, 等. 基于机器视觉的棉纤维长度检测装置及应用方法: 202210642908.7[P].2022-06-08.
[18] 中国纤维检验局. 原棉回潮率试验方法 烘箱法:GB/T 6102.1—2006[S].北京:中国标准出版社,2006.
[19] 翟志强,陈学庚,邱发松,等.基于像素块和机器学习的播前棉田地表残膜覆盖率检测[J].农业工程学报,2022,38(6):140-147.
ZHAI Zhiqiang, CHEN Xuegeng, QIU Fasong, et al. Detecting surface residual film coverage rate in pre-sowing cotton fieldsusing pixel block and machine learning[J]. Transactions of the CSAE, 2022, 38(6): 140-147.(in Chinese)
[20] 杨扬,刘洋,苏宸,等. 基于超分辨率重建与机器学习的油菜苗情监测方法[J].农业机械学报, 2024, 5(6): 196-201.
YANG Yang, LIU Yang, SU Chen,et al. Oilseed rape seedling monitoring method based on super-resolution reconstruction and machine learning[J]. Transactions of the Chinese Society for Agricultural Machinery,2024,55(6):196-201.(in Chinese)
[21] 曹引,冶运涛,赵红莉,等. 基于离散粒子群和偏最小二乘的水源地浊度高光谱反演[J].农业机械学报, 2018, 49(1): 173-182.
CAO Yin, YE Yuntao, ZHAO Hongli,et al. Satellite hyperspectral retrieval of turbidity for water source based on discrete particle swarm and partial least squares[J]. Transactions of the Chinese Society for Agricultural Machinery,2018,49(1):173-182.(in Chinese)
[22] 余坤勇,姚雄,邱祈荣,等.基于随机森林模型的山体滑坡空间预测研究[J].农业机械学报,2016,47(10):338-345.
YU Kunyong, YAO Xiong, QIU Qirong, et al. Landslide spatial prediction based on random forest model[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(10): 338-345.(in Chinese)
[23] 崔永杰,王明辉,张鑫宇,等. 基于支持向量机回归的营养液调控模型研究[J].农业机械学报, 2021, 52(1): 312-323.
CUI Yongjie, WANG Minghui, ZHANG Xinyu, et al. Regulation model research of nutrient solution based on support vector machine regression[J].Transactions of the Chinese Society for Agricultural Machinery,2021,52(1):312-323.(in Chinese)
[24] 张德胜,杨港,赵旭涛,等. 基于BP神经网络的立式离心泵导叶与蜗壳优化设计[J].农业机械学报, 2022, 53(4): 130-139.
ZHANG Desheng, YANG Gang, ZHAO Xutao,et al. Optimization design of vane diffuser and volute in vertical centrifugal pump based on back propagation neural network[J].Transactions of the Chinese Society for Agricultural Machinery,2022,53(4):130-139. (in Chinese)
[25] 周章怀,苏士勋,李庆元,等.X-R质量控制图在熔铸AZS-33测定中的应用[J].玻璃,2023,50(8):29-36.
ZHOU Zhanghuai, SU Shixun, LI Qingyuan, et al.X-R application of quality control chart in the determination of AZS-33[J]. Glass, 2023, 50(8): 29-36.(in Chinese)
[26] 李辉,张俊美,姚佳人,等.质量控制图在钢铁材料碳含量测定中的应用[J].工程机械,2024,55(6):176-182,15.
LI Hui, ZHANG Junmei, YAO Jiaren, et al. Application of quality control charts in determination of carbon content in steel materials[J]. Construction Machinery, 2024, 55(6): 176-182,15.(in Chinese)