充分利用电动机驱动能量利用率高、转速范围宽的优势与高功率密度液压泵相结合,提升流量匹配灵活性,是降低液压动力单元功耗的有效措施[1]。大功率外啮合齿轮泵以其结构简单、成本低、抗污染能力强的优点[2]在电动工程机械中得到广泛应用,并基于电动化、高速化运行条件逐渐向轻量化、小型化发展[3]。然而外啮合齿轮泵在高转速运行时,容积效率大幅减小,能量利用率低,因此优化泵的吸油流道结构,提高齿腔充液率,进而提高容积效率,对降低能量损失具有重要意义。
提升液压泵容积效率的方法可分为两种。一种方法是利用数值模拟[4]和试验[5]对泵本体结构进行优化。由于外啮合齿轮泵端面泄漏量约占总泄漏量的70%[6],所以可通过优化侧板支撑方式[7]、改善齿轮端面润滑状态[8-10]、优化齿轮配合间隙[11-12]减少泄漏量,进而提高泵的容积效率。除此之外,卸荷槽[13]、齿数[14]、齿的线型[15]、吸油口尺寸[16-17]及方向[18]也会影响泵的性能。另一种方法是在泵的入口增加吸油增压装置,抵消泵的吸油阻力,缩短油液进入齿腔的时间。常用的增压方式有油箱增压[19]、射流泵增压[20]、离心泵增压[21]。文献[22-23]将电动机、空心轴离心泵和内啮合齿轮泵相结合形成高度集成的电机泵,内啮合齿轮泵在高转速时表现出较好的吸油性能。
本文首先通过试验对外啮合齿轮泵容积效率进行测试,并建立齿腔吸油流量-压力数学模型,对齿腔充液率低的原因进行理论分析。然后提出一种新的吸油流道结构,并利用数值模拟的方法对结构参数进行优化。最后利用试验验证优化结构的有效性。
测试对象为排量63 cm3/r的传统外啮合齿轮泵。试验台如图1所示,油箱内装有HM46抗磨液压油,电动机驱动外啮合齿轮泵转动,油液从油箱内被吸出,经吸油管进入齿轮泵,并从排油管排出返回油箱。其中,外啮合齿轮泵进出口均安装有精度分别为0.25%和0.1℃的压力传感器和温度传感器,用来测量油液的压力和温度,排油管路上安装有精度为0.5%的涡轮流量计用来测量体积流量。相关数据均被数据采集系统采集和记录,采集频率10 Hz。

图1 外啮合齿轮泵试验系统
Fig.1 Experiment system for external gear pump
1.油箱 2.开关阀 3.电动机 4.吸油管 5.入口温度传感器 6.入口压力传感器 7.外啮合齿轮泵 8.出口压力传感器 9.数据采集系统 10.出口温度传感器 11.排油管 12.涡轮流量计
试验在油温44.3℃、环境温度27.3℃、泵空载条件下进行。泵稳定运行后,数据采集20 s。获得不同转速下齿轮泵容积效率ηC,如图2所示。
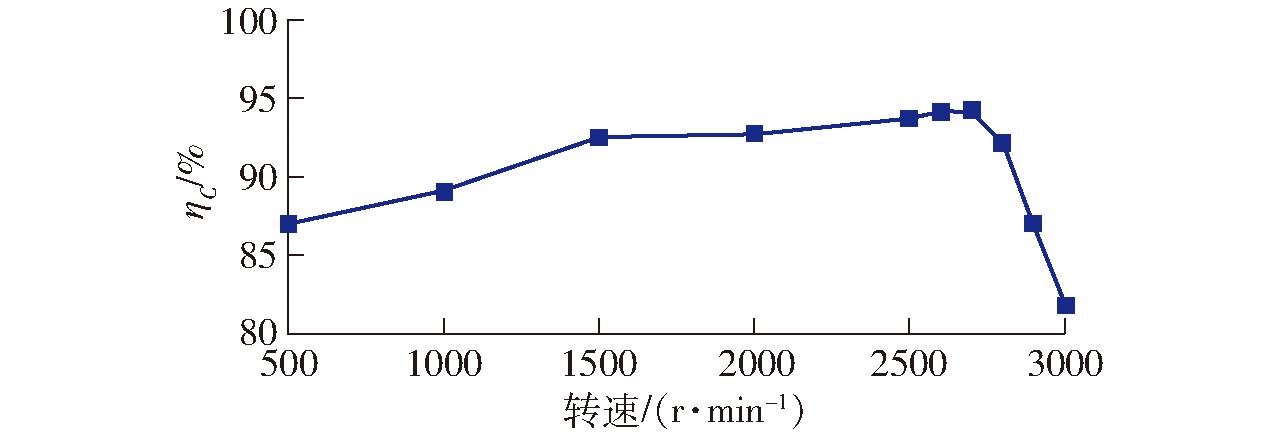
图2 传统泵在不同转速下的容积效率
Fig.2 Volume efficiency of gear pump at different speeds
由图2可知,随转速的升高,容积效率从 500 r/min 时的87.97%开始缓慢增加,到转速 2 700 r/min 时达到最大值94.2%;然后容积效率迅速减小,在3 000 r/min时减小至81.87%,相较于最大容积效率降低12.33个百分点。为探究传统泵高转速运行容积效率突降的原因,建立外啮合齿轮泵齿腔吸油流量-压力数学模型,进行理论分析。
齿轮泵三维模型如图3所示。其中齿轮模数m为5 mm,齿数z为12,齿宽B为29 mm,齿顶圆直径Da、齿根圆直径Df、中心距h分别为73.5、48.3、62.8 mm。
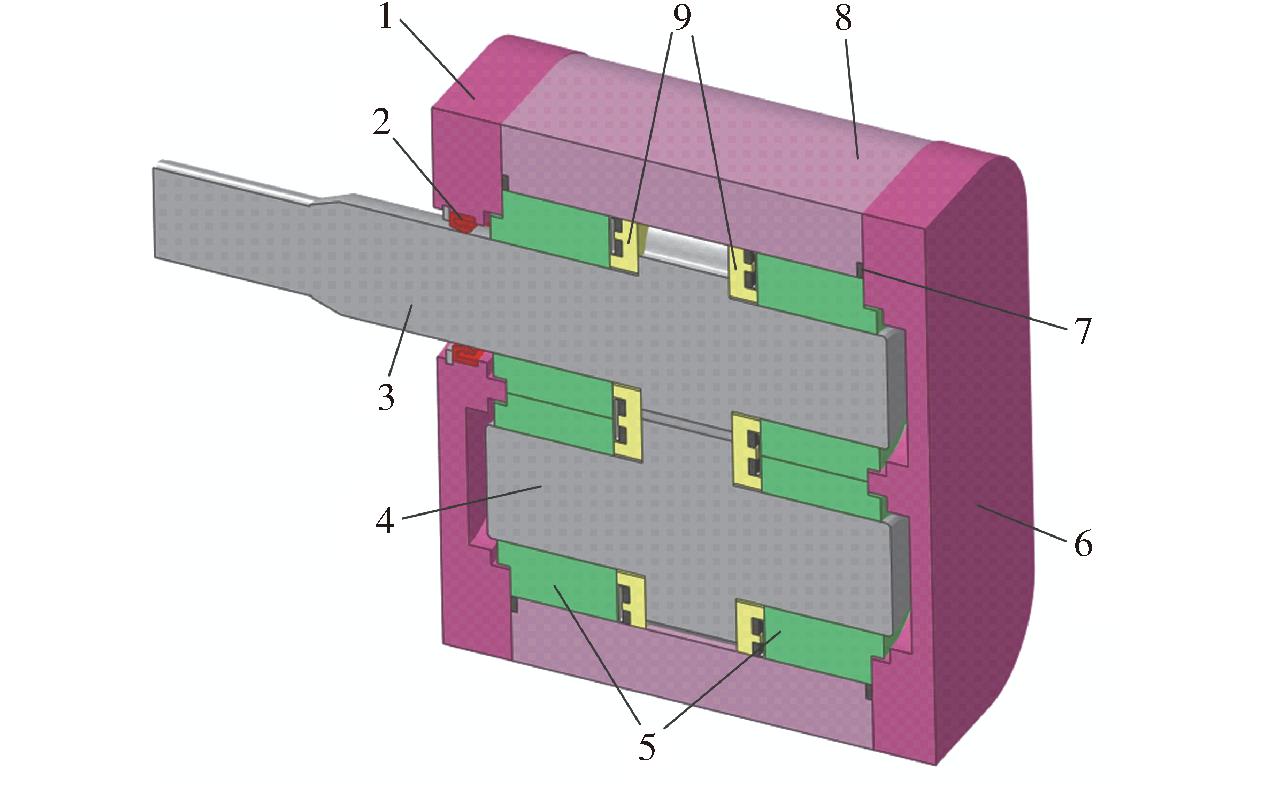
图3 齿轮泵三维模型示意图
Fig.3 3D structure diagram of external gear pump
1.前端盖 2.唇形密封圈 3.主动齿轮轴 4.从动齿轮轴 5.轴套 6.后端盖 7.端面密封圈 8.泵体 9.浮动侧板
进入吸油口齿腔内的流量取决于两齿脱离啮合后形成的最小面积区域A。假设齿轮运动至一定角度,该角度的吸油状态视为静态,则满足从吸油口流经A至齿腔的瞬时流量q所需的A两侧最小压力差为Δp。为清晰表示变量之间的关系,假设径向吸油时的最小吸油面积为Ar,最小压力差为Δpr;轴向吸油时的最小吸油面积为Aa,最小压力差为Δpa;齿腔最小容积为V。径向吸油和轴向吸油的油液流动方向示意图如图4所示。
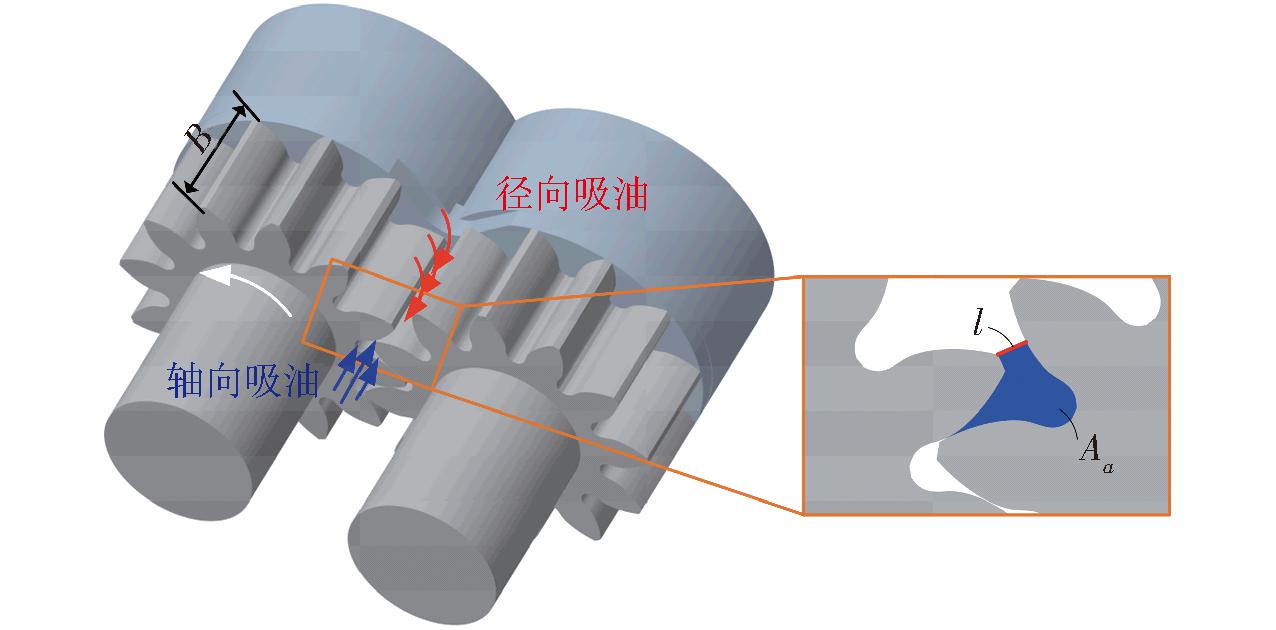
图4 不同吸油方向示意图
Fig.4 Diagram of different oil absorption directions
利用三维模型进行测量并拟合两齿之间最短距离l和轴向吸油面积Aa随齿轮转角θ的变化规律,获得Ar、Aa、V计算公式为
Ar=lB
(1)
Aa=226.84θ2-1.9θ+10.74![]()
(2)
V=AaB
(3)
其中

(4)
θ=ωt
(5)
(6)
式中 n——齿轮转速,r/min
ω——齿轮角速度,rad/s
由文献[24]可得压力-流量关系式
(7)
式中 Cd——流量系数 ρ——密度
A——最小面积
式(7)可变换为
(8)
其中
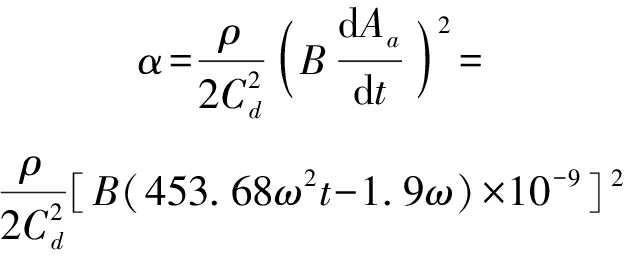
(9)
将式(1)代入式(8)可得采用径向吸油时的最小压力差Δpr,将式(2)代入式(8)可得采用轴向吸油时的最小压力差Δpa。Δpr和Δpa均为角速度ω的函数,公式为
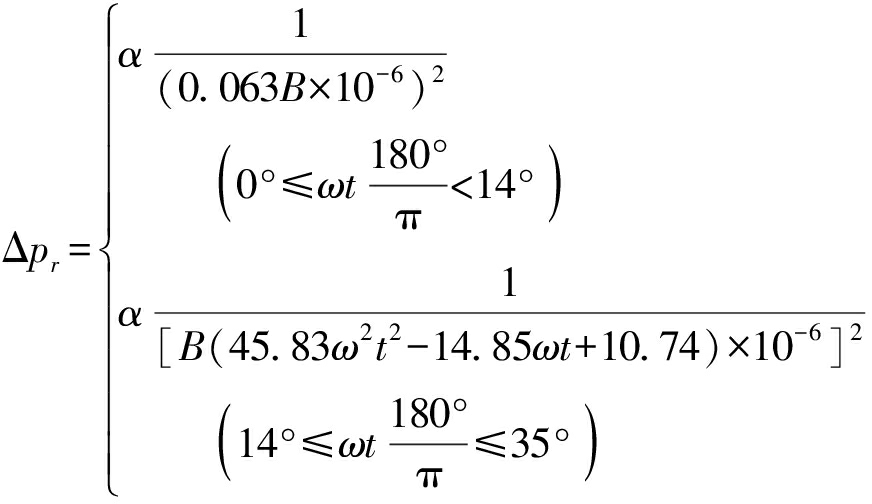
(10)
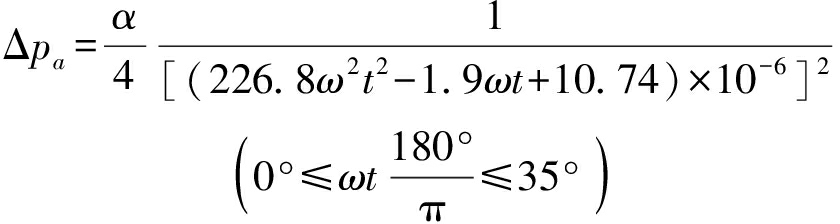
(11)
取系数Cd为0.72[6]、ρ为860 kg/m3,计算V及Δpr随θ的变化曲线,如图5a所示,将Δpr在0~0.2 MPa 区间内曲线展示见图5b,其中黄色区域为转速2 000 r/min时,Δpr≥0.1 MPa的最小齿腔容积。
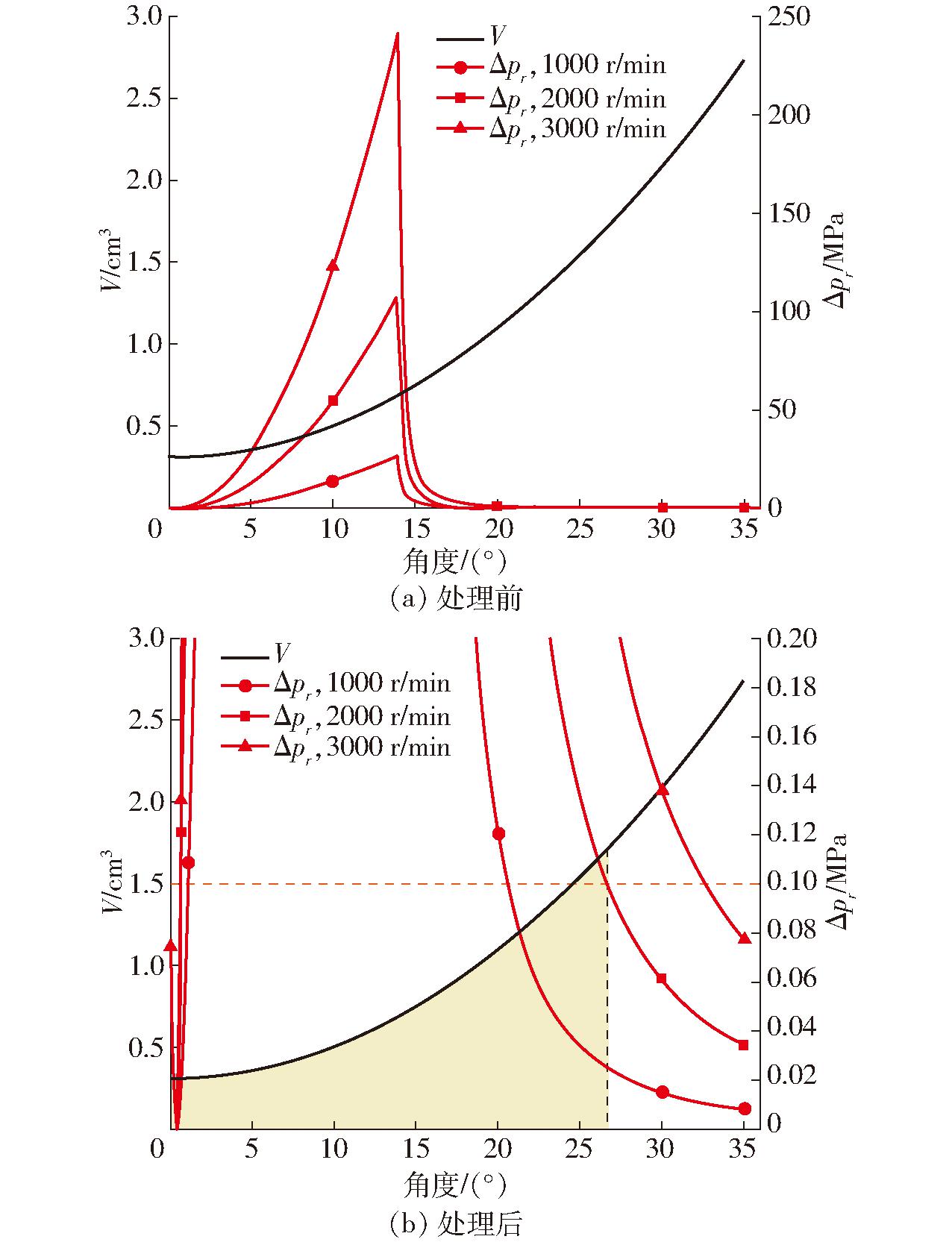
图5 V和Δpr随θ的变化曲线
Fig.5 V and Δpr change curves with θ
由图5可以得到,径向吸油时,转速为1 000、2 000、3 000 r/min,Δpr≥0.1 MPa的最小齿腔容积占齿腔总容积比例分别为29.77%、52.55%、83.07%。然而,由于泵入口为大气压,不能提供如图5a所示的巨大压力,齿腔吸油不足,齿腔内会形成极低的负压,从而产生如图6a、6b(图中θ0表示初始角度)所示的由瞬时射流冲击引起的空化涡流,直至图6c所示径向面积增大后涡流消失。需要指出的是,该可视化试验在500 r/min情况下进行,若转速增加,则齿腔充液时间缩短,充液不足的现象会随之加剧。
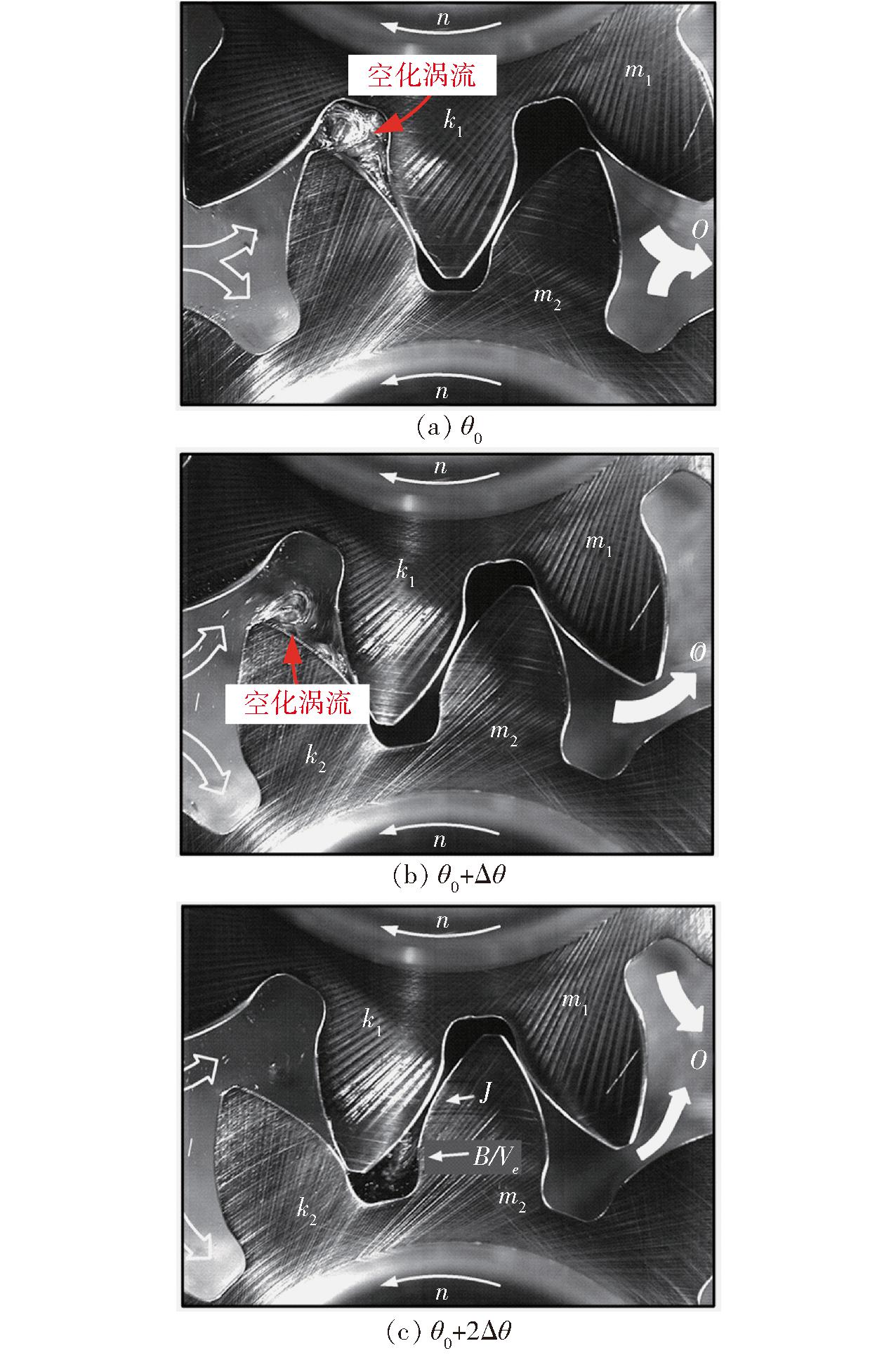
图6 齿腔内的空化现象[25]
Fig.6 Cavitation in tooth cavity
若采用轴向吸油,则计算V及Δpa随θ的变化曲线如图7所示,其中黄色区域为转速2 000 r/min时,Δpa≥0.1 MPa的最小齿腔容积。由图7可知,Δpa相较Δpr大幅下降,这可有效减轻齿腔内的空化现象。转速为1 000、2 000、3 000 r/min,Δpa≥0.1 MPa 的最小齿腔容积占比分别为0、42.92%、96.88%,比Δpr分别减少29.77、9.63、-13.81个百分点。轴向吸油在较低转速下对减少大压差的齿腔容积占比具有明显作用,但在高转速3 000 r/min时仍不明显。
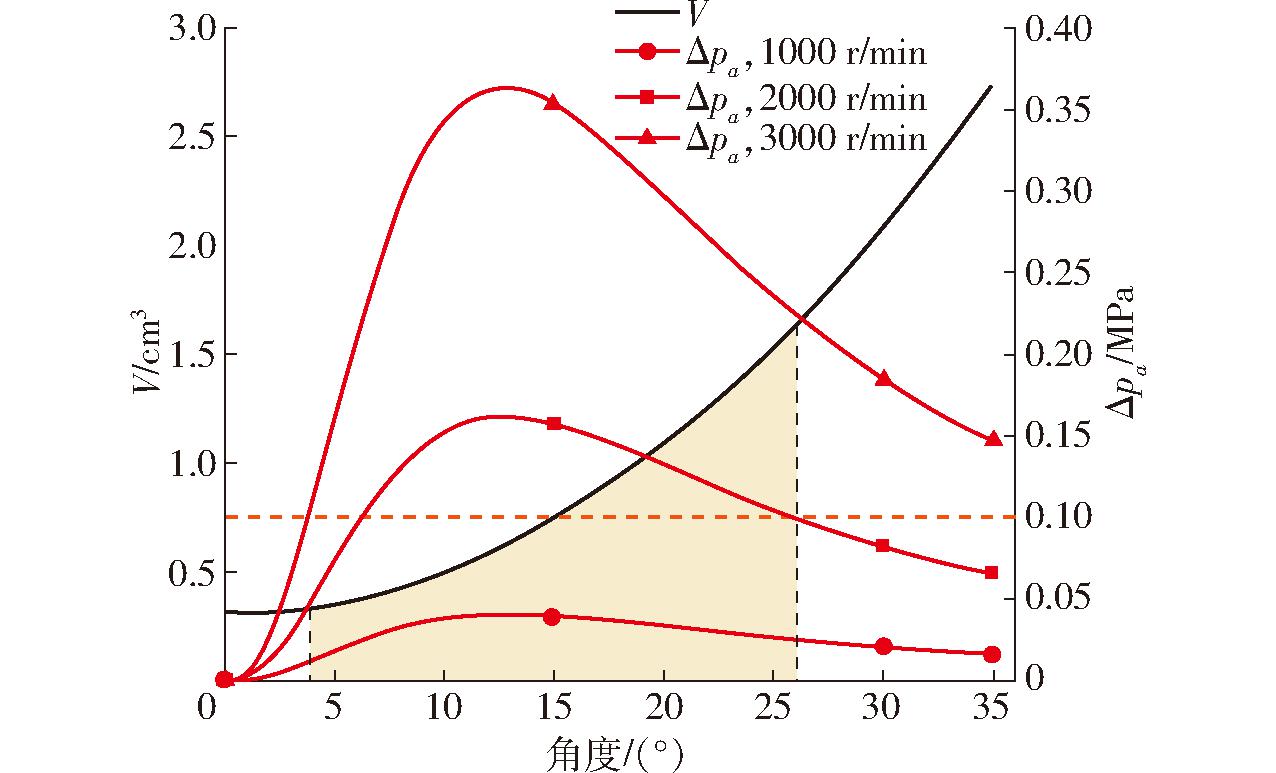
图7 V和Δpa随θ的变化曲线
Fig.7 V and Δpa change curves with θ
为减小Δp幅值并减少Δp≥0.1 MPa的最小齿腔容积占比,采用联合吸油方式,即以轴向吸油为主,径向吸油为辅。
按照吸油面积分配流量,则径向吸油流量qr,c和轴向吸油流量qa,c计算公式为
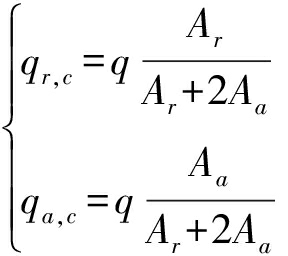
(12)
同理,径向齿腔分配容积Vr,c和轴向齿腔分配容积Va,c计算公式为
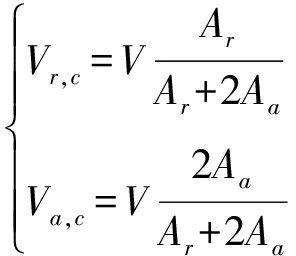
(13)
将式(12)代入式(8)可得
(14)
其中下标i表示所选择的吸油方式,r表示径向吸油,a表示轴向吸油。
图8为式(13)和式(14)计算得到的结果。Δpr,c较Δpr大幅减小,但Δpa,c与Δpa基本相同。转速在1 000、2 000、3 000 r/min,高于0.1 MPa的最小总齿腔容积占比分别为4.26%、22.5%、40.45%,相较单独径向吸油时分别减小25.51、30.05、42.62个百分点,相较单独轴向吸油时分别减小-4.26、20.42、56.43个百分点,联合吸油方式表现出较好的吸油性能。
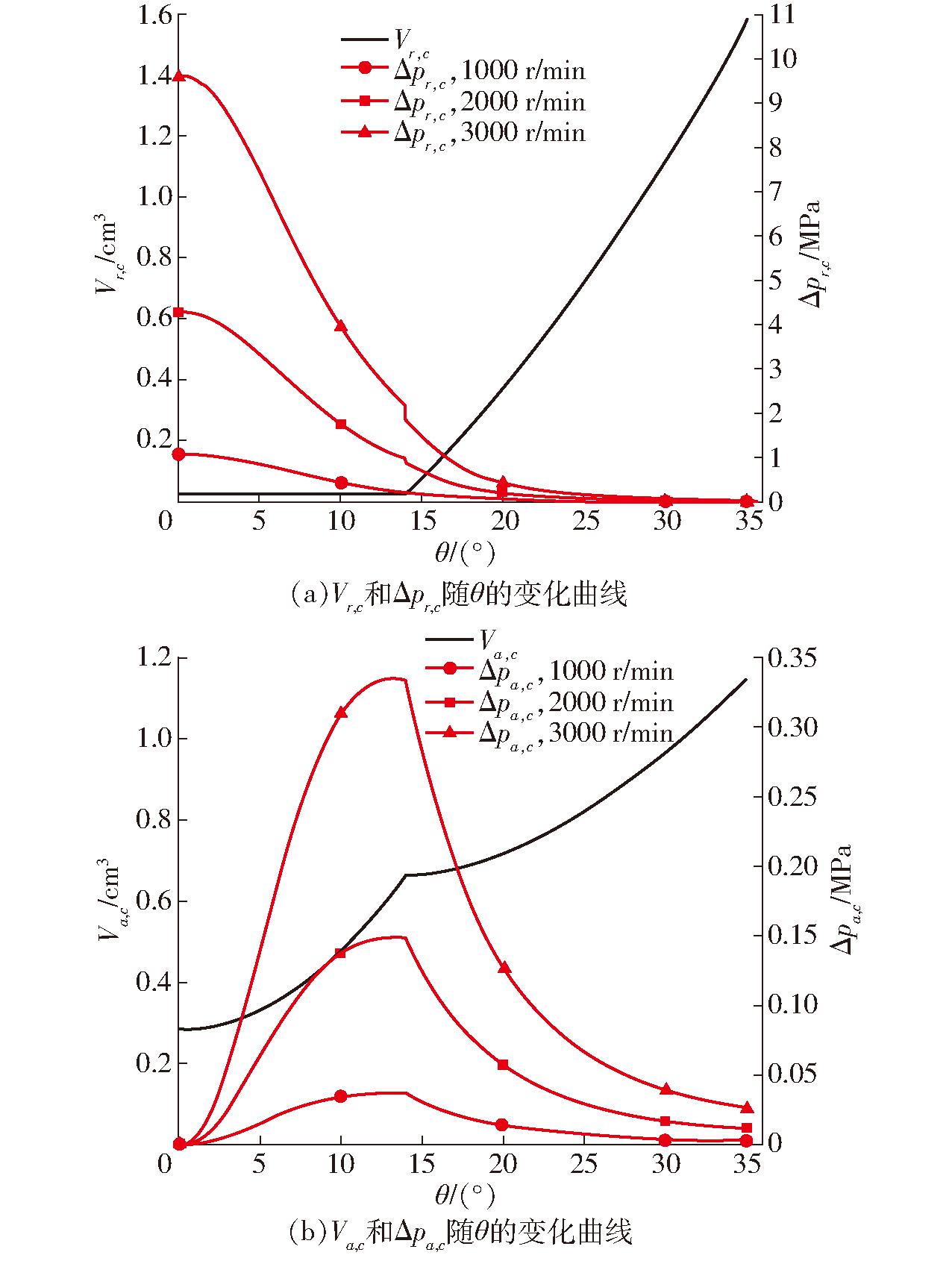
图8 Vi,c及Δpi,c随θ的变化曲线
Fig.8 Vi,c and Δpi,c change curves with θ
综合以上理论分析可知,径向吸油时,由于过流面积小,齿腔充满油液时所需的瞬时压力较大,而泵入口压力接近大气压,无法满足齿腔充液需求,导致齿腔充液率降低,发生空化现象,且泵高转速运行时,齿腔充液时间缩短,是泵高转速运行时容积效率降低的主要原因。通过增大吸油面积可有效解决高转速下齿腔充液率低的问题。
为增加齿腔吸油过流面积,将浮动侧板和轴套开设“π”形槽,如图9所示。浮动侧板和轴套的“π”形槽形成轴向吸油流道,轴向吸油流道与吸油卸荷槽直接连通。

图9 基于“π”形槽设计的浮动侧板和轴套三维结构示意图
Fig.9 3D structure diagram of floating lateral plate and shaft sleeve based on “π” groove design
优化后泵的流体域如图10所示。其中入口流体域由径向吸油流道、轴向吸油流道和吸油卸荷槽流道3部分构成。
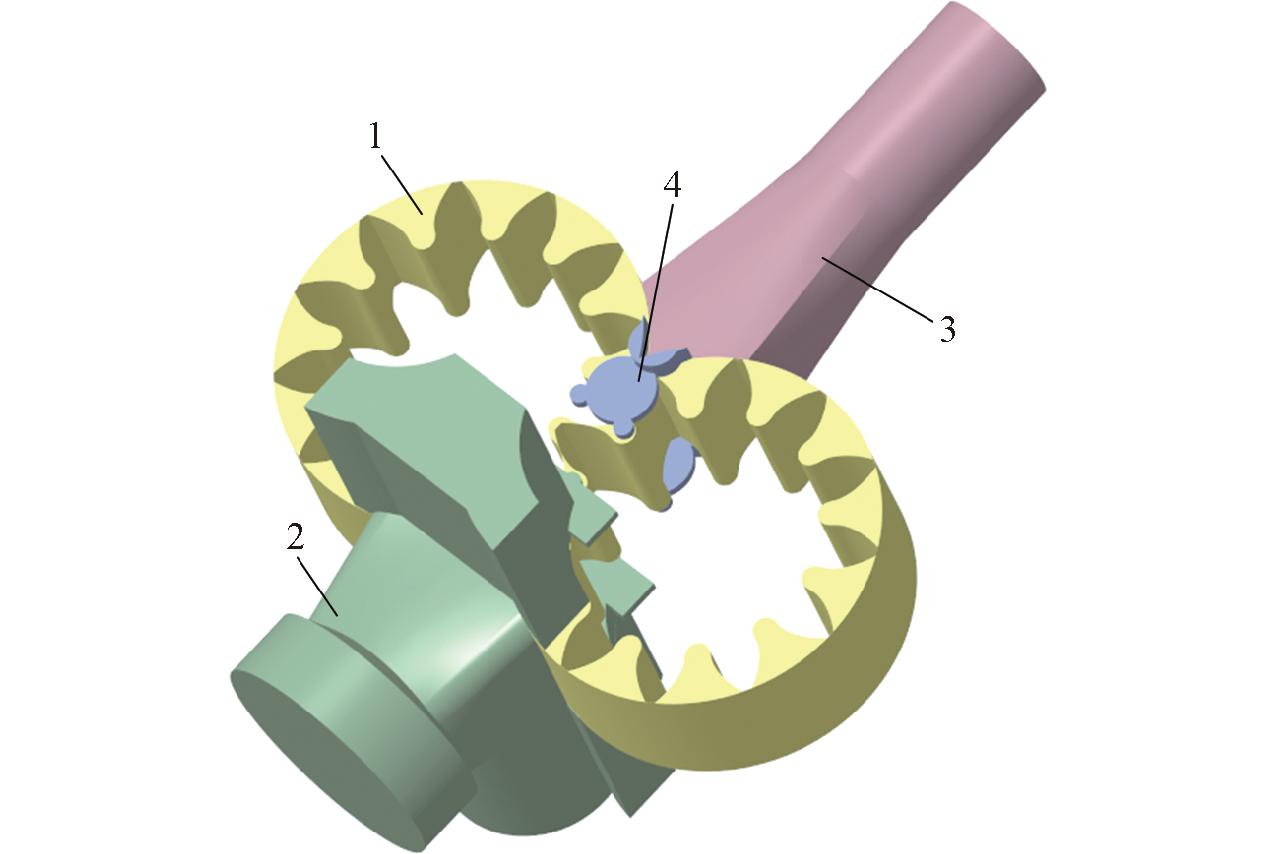
图10 优化泵的三维流场示意图
Fig.10 3D structure diagram of optimized external gear pump
1.齿轮流体域 2.入口流体域 3.出口流体域 4.排油卸荷槽流体域
网格过多会增加计算时间,过少会降低计算精度。为选取合适的网格数量,利用Pumplinx流场仿真软件对不同网格数泵出口流量进行监测。湍流模型选择Standard k-ε模型,绝对入口压力设为0.1 MPa,绝对出口压力设为0.3 MPa,油液动力粘度设为0.037 Pa·s,齿轮转速设为2 200 r/min。
仿真结果如图11所示。时均体积流量随网格数量的增加而增加。当网格数量为 7.6×105 和1.13×106时,容积效率之间仅相差0.13%,满足网格无关性和计算精度要求。因此,综合考虑计算的时间成本和精度,本模型选择网格数7.6×105 ~8.5×105。
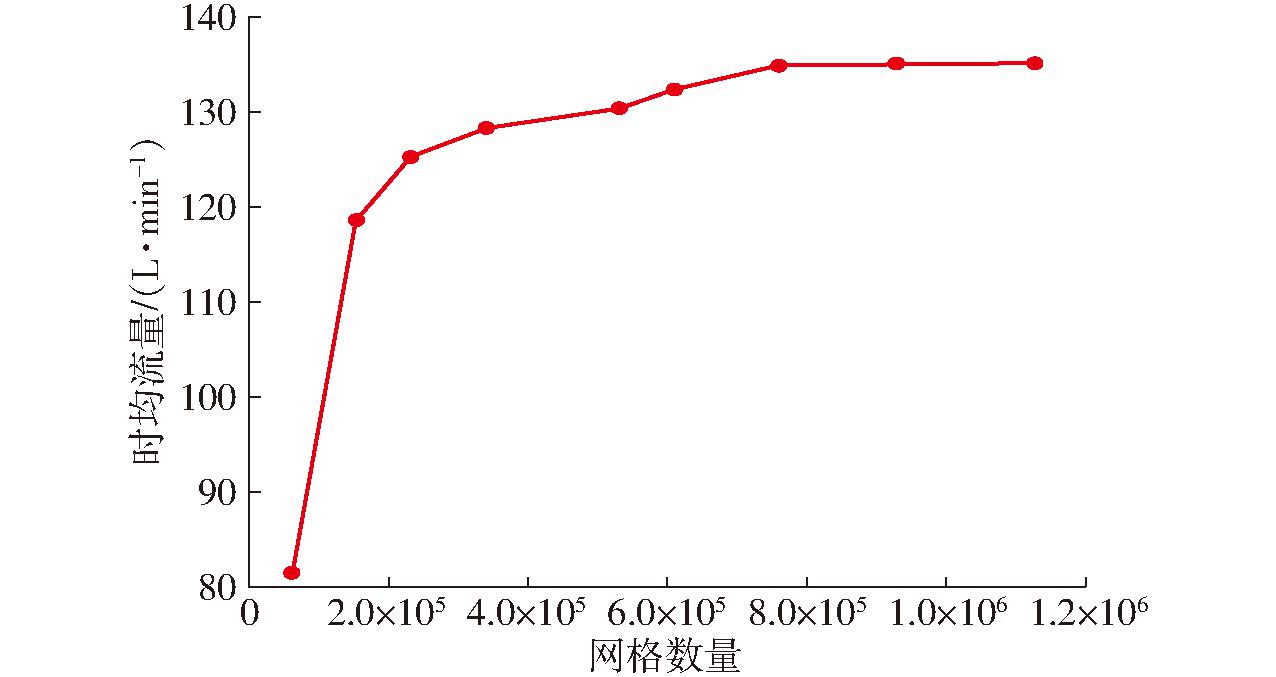
图11 时均流量随网格数量变化曲线
Fig.11 Time mean flow curve with number of grids
如图12为“π”形槽关键结构参数,包括圆弧半径Rm、顶边间距d1、侧边间距d2。为探究结构参数对泵容积效率ηN的影响,设计正交试验表和仿真得到的容积效率如表1所示。其中仿真转速设为3 000 r/min。
表1 全因子正交试验设计
Tab.1 Full factor orthogonal experiment design
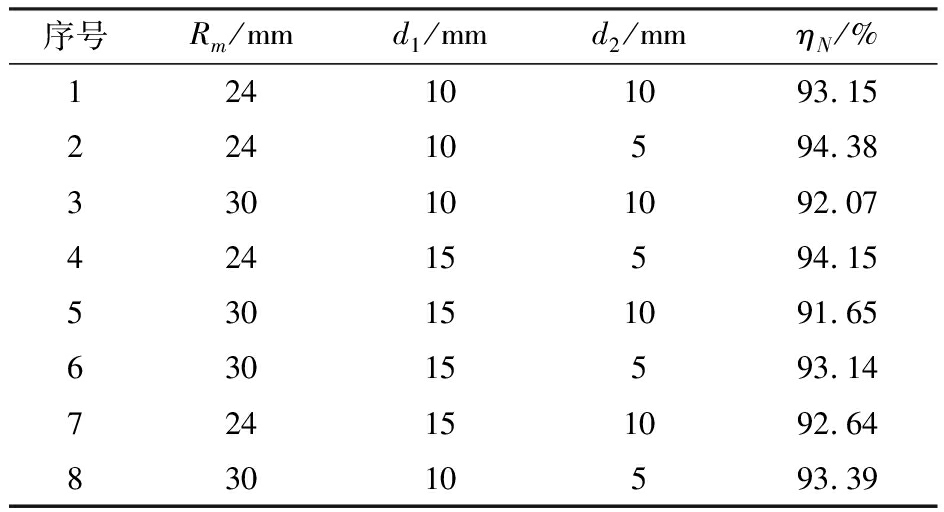
序号Rm/mmd1/mmd2/mmηN/%124101093.1522410594.38330101092.0742415594.15530151091.6563015593.14724151092.6483010593.39
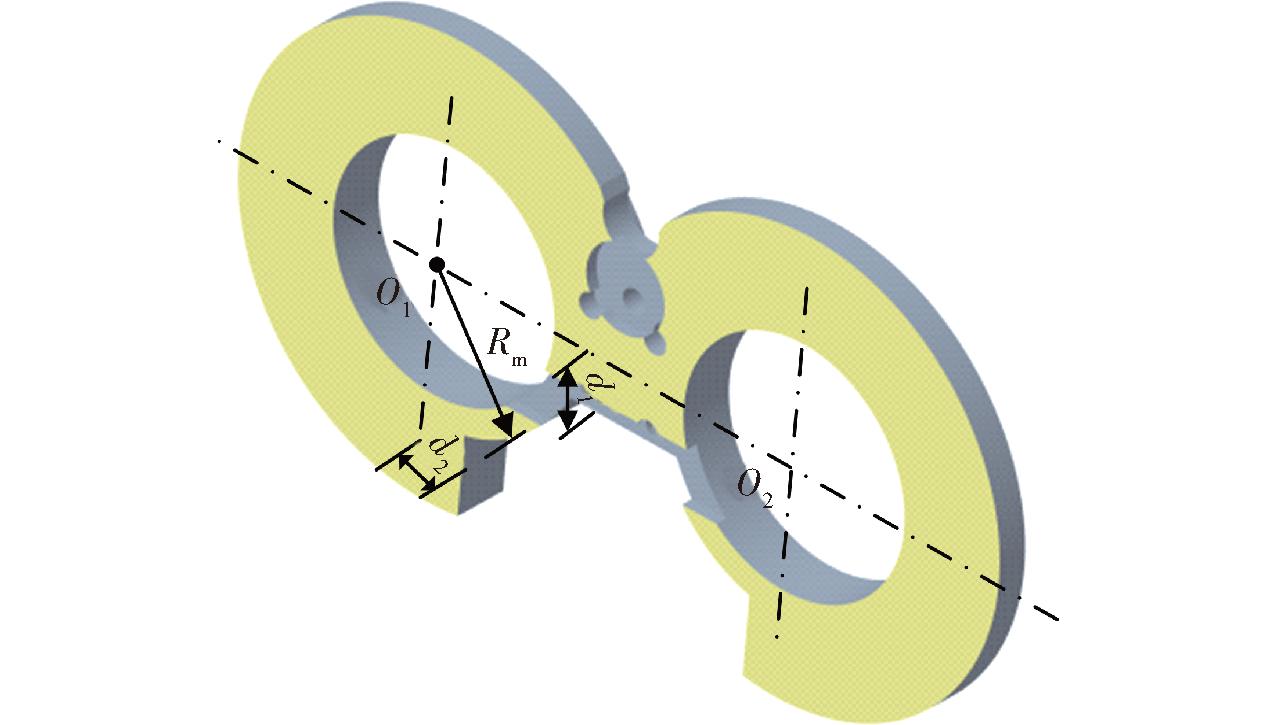
图12 “π”形槽关键结构参数
Fig.12 Key structural parameters of “π” groove
利用Minitab创建响应变量为容积效率、显著性水平为0.05的标准化正态效应图和效应Pareto图,如图13所示。由图13a可知,主项Rm、d1、d2效应显著,其中d2离中心线最远,其次是Rm,最后是d1,说明对优化泵容积效率影响程度从大到小依次为d2、Rm、d1。此外,所有主项在中心线的负方向,说明主项数值越大,泵的容积效率越低。
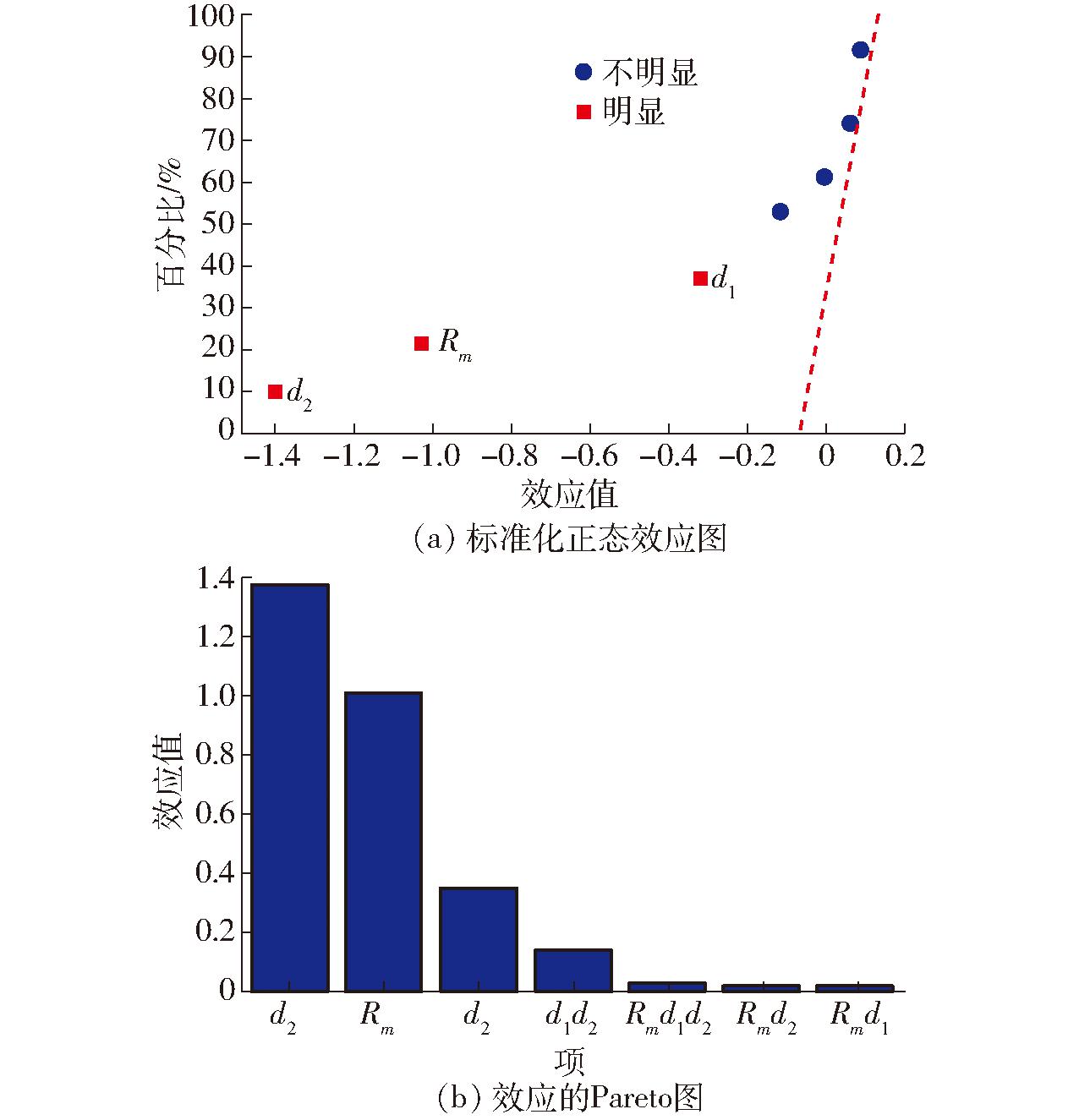
图13 标准化正态效应图和效应的Pareto图
Fig.13 Normalized normal effect diagram and Pareto diagram of effect
由图13b可以得到,效应阈值为0.142。忽略Pareto图中未超过阈值且数值较小的交叉项,使用响应函数建立ηN预测模型
ηN=99.747-0.169 4Rm-0.001 8d1-
0.163 3d2-0.009 1d1d2 (R2=0.997 1)
(15)
由于结构尺寸限制,选择满足max{ηN}的设计值Rm=24 mm、d1=10 mm和d2=5 mm进行试验验证。优化后浮动侧板和轴套实物图如图14所示。将其装入外啮合齿轮泵中,在图1所示试验系统中进行测试。

图14 优化后浮动侧板和轴套的实物图
Fig.14 Optimized floating lateral plate and shaft sleeve
测试油温为41.7℃,环境温度为23.7℃,其余测试条件相同。获得不同转速下优化泵容积效率ηN和容积效率差ηN-ηC,如图15所示。
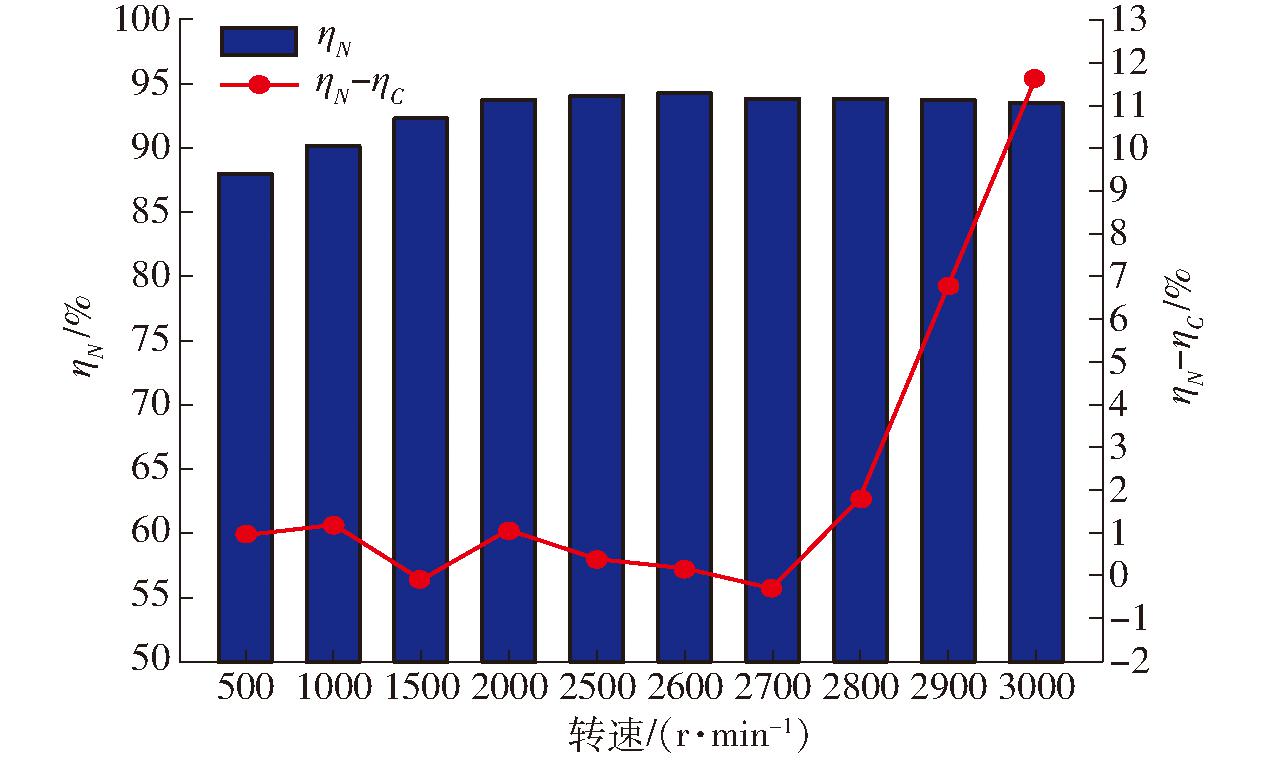
图15 容积效率对比曲线
Fig.15 Volume efficiency comparison curve
由图15可知,优化泵容积效率在转速500~2 000 r/min 内呈近似线性增加,2 000~2 600 r/min缓慢增加,在2 600 r/min时达到最大值94.27%,超过转速2 600 r/min后缓慢减小,在3 000 r/min时容积效率为93.51%。与图2所示优化前泵容积效率ηC相比,优化泵在500~2 700 r/min内容积效率相差较小,在2 800、2 900、3 000 r/min时容积效率分别提高1.8、6.79、11.64个百分点,可认为2 700 r/min为容积效率提升的临界转速。优化泵在高转速运行时具有明显优势。
(1)传统结构的大功率外啮合齿轮泵高转速运行时容积效率较低。随转速的升高,传统泵容积效率从500 r/min时的87.97%开始缓慢增加,到转速2 700 r/min时达到最大值94.2%;然后容积效率迅速减小,在3 000 r/min时减小到81.87%,相较于最大容积效率减小12.33个百分点。
(2)径向吸油时,由于过流面积小,齿腔充满油液时所需的瞬时压力较大,而泵入口压力接近大气压,无法满足齿腔充液需求,导致齿腔充液率降低发生空化现象,且高转速运行时,齿腔充液时间缩短,是泵高转速运行时容积效率降低的主要原因。
(3)齿腔吸油流量-压力理论模型分析表明联合吸油方式具有明显效果。联合吸油方式在1 000、2 000、3 000 r/min高于0.1 MPa的总齿腔容积占比分别为4.26%、22.5%、40.45%,相较单独径向吸油时分别减小25.51、30.05、42.62个百分点,相较单独轴向吸油时分别减小-4.26、20.42、56.43个百分点。
(4)结构参数Rm、d1、d2均对优化泵容积效率有明显影响,影响程度从大到小依次为d2、Rm、d1。结构参数数值越大,泵的容积效率越低。容积效率预测模型R2为0.997 1,具有较高精度。基于预测模型和结构尺寸限制,使容积效率在3 000 r/min高转速运行时最大的结构尺寸为Rm=24 mm、顶边间距d1=10 mm、侧边间距d2=5 mm。
(5)经试验验证,优化泵在高转速运行时具有较高的容积效率。优化泵容积效率在转速500~2 000 r/min 内呈近似线性增加,2 000~2 600 r/min缓慢增加,在2 600 r/min时达到最大值94.27%,超过转速2 600 r/min后缓慢减小,在3 000 r/min时容积效率为93.51%。与传统泵容积效率相比,优化泵在2 800、2 900、3 000 r/min时容积效率分别提高1.8、6.79、11.64个百分点,可认为2 700 r/min为优化泵容积效率开始明显提升的临界转速。
[1] 林元正, 林添良, 陈其怀, 等. 电动工程机械关键技术研究进展[J]. 液压与气动, 2021, 45(12): 1-12.
LIN Yuanzheng, LIN Tianliang, CHEN Qihuai,et al. Research progress on key technologies of electric construction machinery[J]. Chinese Hydraulics &Pneumatics, 2021, 45(12): 1-12. (in Chinese)
[2] MICHAEL P, KHALID H, WANKE T. An investigation of external gear pump efficiency and stribeck values[C]∥SAE 2021 Commercial Vehicle Engineering Congress. Rosemont, 2012: 2041.
[3] 车明阳. 微小型外啮合齿轮泵的研制[D]. 哈尔滨:哈尔滨工业大学, 2020.
CHE Mingyang.Develpoment of miniature external gear pump[D]. Harbin: Harbin Institute of Technology, 2020. (in Chinese)
[4] BÜGENER N, HELDUSER S. Analysis of the suction performance of axial piston pumps by means of computational fluid dynamics (CFD)[C]∥7th International Fluid Power Conference. Aachen, 2010: 641-654.
[5] MILANI M, MONTORSI L, PALTRINIERI F. Experimental investigation of the suction capabilities of an innovative high speed external gear pump for electro-hydraulic actuated automotive transmissions[J]. International Journal of Fluid Power, 2024, 25(2): 243-272.
[6] 林建亚,何存兴.液压元件[M]. 北京:机械工业出版社, 1988.
[7] BORGHI M, MILANI M, PALTRINIERI F, et al. Studying the axial balance of external gear pumps[C]∥SAE 2005 Commercial Vehicle Engineering Congress. Rosemont, 2005: 3634.
[8] KOÇ E. Analytical and experimental investigation into the sealing and lubrication mechanisms of the gear ends in pumps[J]. Wear, 1989, 135(1):79-94.
[9] KOÇ E. Bearing misalignment effects on the hydrostatic and hydrodynamic behaviour of gears in fixed clearance end plates[J]. Wear, 1994, 173(1-2):199-206.
[10] KOÇ E, NG K, HOOKE C J. An analysis of the lubrication mechanisms of the bush-type bearings in high pressure pumps[J]. Tribology International, 1997, 30(8): 553-560.
[11] ZHAN Peng, WEI Liejiang, LIU Rongmin, et al. Flow field modeling and simulation of high-speed gear pump considering optimal radial and end clearance[J]. IEEE Access, 2023, 11: 64725-64737.
[12] 陈鼎,张杨,叶绍干,等.配合间隙对直线共轭内啮合齿轮泵流场特性的影响[J]. 农业机械学报, 2024, 55(2): 442-449.
CHEN Ding, ZHANG Yang, YE Shaogan, et al. Influence of mating clearance on flow field characteristics of linear conjugate internal gear pump[J]. Transactions of the Chinese Society for Agricultural Machinery, 2024, 55(2): 442-449. (in Chinese)
[13] LIU Hongru, PAN Mengni, FU Jiangfeng, et al. A new type unloading groove design and simulation for engine fuel gear pump[C]∥13th International Conference on Mechanical and Aerospace Engineering. IEEE, 2022: 86-90.
[14] IVANOV V, KARAIVANOV D, IVANOVA S, et al. Gear mesh geometry effect on performance improvement for external gear pumps[C]∥MATEC Web of Conferences, EDP Sciences, 2019: 01007.
[15] ZHAO Xinran, VACCA A. Analysis of continuous-contact helical gear pumps through numerical modeling and experimental validation[J]. Mechanical Systems and Signal Processing, 2018, 109: 352-378.
[16] 杨国来, 王文宇, 黄付田, 等. 不同吸油口尺寸及转速下齿轮泵空化特性[J]. 液压与气动, 2020,44(1): 74-79.
YANG Guolai, WANG Wenyu, HUANG Futian, et al. Cavitation characteristics of gear pumpunder different suction port sizes and speeds[J]. Chinese Hydraulics &Pneumatics, 2020,44(1): 74-79. (in Chinese)
[17] EL-HADJ A A, SHAYFULL Z B A R. Optimization of an external gear pump using response surface method[J]. Journal of Mechanics, 2020, 36(4): 567-575.
[18] BÜGENER N, KLECKER J, WEBER J. Analysis and improvement of the suction performance of axial piston pumps in swash plate design[J]. International Journal of Fluid Power, 2014, 15(3): 153-167.
[19] FAN Xiaoxuan, ZHAO Dingxuan, ZHAO Xiaolong, et al. Design of shipborne constant pressure pressurized tank and constant pressure control[C]∥IEEE 8th International Conference on Fluid Power and Mechatronics. IEEE, 2019: 1042-1048.
[20] ROMANENKO I, BILOHUB O. Increasing the efficiency of the operating cycle of a high-pressure fuel gear pump by using a jet pump as a booster stage[J]. Aerospace Technic and Technology, 2023(2): 38-45.
[21] 杨胜清, 冀宏, 李晨, 等. 高速运行齿轮泵的吸油空化与抑制[J]. 液压与气动, 2024, 48(8):18-28.
YANG Shengqing, JI Hong, LI Chen, et al. Suction cavitation andsuppression of high-speed gear pump[J]. Chinese Hydraulics &Pneumatics, 2024, 48(8):18-28. (in Chinese)
[22] 李小平, 冀宏, 张继铭, 等.气隙非浸油式电机叶片泵的主泵吸油配流设计[J].农业工程学报, 2016, 32(10):54-59.
LI Xiaoping, JI Hong, ZHANG Jiming, et al. Design of suction flow distributor of main pump in non-oil-immersed air gap type hydraulic electro-motor pump[J]. Transactions of the CSAE, 2016, 32(10):54-59. (in Chinese)
[23] SUN Fei, JI Hong, YANG Shengqing, et al. Numerical investigation on pairing solutions of non-positive displacement pumps and internal gear pump for high-speed design[J]. Fluids, 2023, 8(6): 178.
[24] VACCA A, FRANZONI G. Hydraulic fluid power: fundamentals, applications, and circuit design[M]. Hoboken: John Wiley &Sons, 2021.
[25] STRYCZEK J, ANTONIAK P, JAKHNO O, et al. Visualization research of the flow processes in the outlet chamber-outlet bridge-inlet chamber zone of the gear pumps[J]. Archives of Civil and Mechanical Engineering, 2015, 15(1): 95-108.