精密微动缩小机构广泛应用于狭小空间内的高精度运动控制,其核心功能在于将输入位移进行缩小,从而实现更小的运动步长和更高的运动精度[1-3]。此类机构能够在有限的空间内提供灵活且精准的运动,因而适用于半导体制造、光学器件组装和生物医学工程等领域[4-9]。在半导体制造中,它能够实现精确的晶圆对准和图案转移,提高芯片制造的良品率和性能;在光学器件组装中,它确保光学元件精确定位,提升光学系统整体性能;在生物医学工程中,它有助于显微手术和细胞操作的精确控制,减少对生物组织的损伤,增加操作成功率[10]。
秦宇等[11]基于柔性铰链杠杆结构提出一种柔性位移缩小机构,该柔性位移缩小机构行程达10 μm,分辨率可达10 nm。文献[12-13]基于多级缩小的思路设计了一种用扭转板簧铰链组成的位移缩小机构,该机构可以提供1 000倍的缩小比,但由于其机构具有多个零部件,加工较为困难。然而,现有的微动缩小机构研究大多未考虑附加运动位移的存在。因此,设计一种易于加工、无附加运动的微动缩小机构具有重要意义。
学者们对微动机构研究主要集中在定位精度、机构优化等方面[14-15],但在精密操作和高精度要求的场合,机构刚度成为影响其性能的关键因素。刚度不足会导致系统响应不稳定,降低控制精度和可靠性[16-17]。郑洋洋等[18]基于传递矩阵法建立了一种包含5个柔性铰链的柔性杠杆放大微动机构的刚度模型,但这需要进行大量力学分析和矩阵计算。于靖军等[19]提出了一种扩展伪刚体模型法,对包含5个柔性铰链的机构建立了108个方程组,得出其刚度矩阵。WU等[20]针对包含24个柔性铰链的机构,采用解析法和拉格朗日法进行刚度计算。现有刚度分析方法普遍存在力学分析复杂、计算量大等问题,尤其在处理复杂微动机构时,这些问题尤为突出。随着对产品质量和生产效率要求的不断提高,微动缩小机构需具备高刚度和高动态响应特性,以确保在复杂环境下的稳定性和可靠性。因此,一种简单、有效的微动机构刚度分析方法尤为必要。
本文设计一种无附加运动精密微动缩小机构,采用有限元法完成机构无附加运动运力分析;通过等效刚度法对所设计机构进行刚度性能分析,在不同载荷条件下利用有限元分析方法对精密微动缩小机构变形进行模拟分析,并通过实验获得实际刚度,通过有限元及实验分析结果以验证等效刚度法对所设计的微动机构刚度分析的正确性及有效性。
柔性铰链基于自身材料弹性变形实现运动、力或能量传递,具有免装配、无间隙、无摩擦、无磨损、超高运动分辨率等特性,被广泛应用于精密传动领域[21-23]。
柔性铰链可以分为:矩形柔性铰链(图1a)、弧线式柔性铰链(图1b)和直圆式柔性铰链(图1c)[24-26]。如图1所示,矩形柔性铰链运动范围大,但其在运动过程中转动重心会移位;弧线式柔性铰链虽具备了很大运动精度,但运动范围太小;而直圆式柔性铰链在保证较高运动精度的同时还能保证具有一定的运动范围。因此,本文设计的精密微动缩小机构选用直圆式柔性铰链。

图1 柔性铰链分类
Fig.1 Flexible hinge classification
精密微动缩小机构缩小功能是通过柔性铰链杠杆原理来实现,如图2所示。柔性铰链c距离柔性铰链a位移为l2,柔性铰链b距离柔性铰链a位移为l1。初始状态下,右端点q为固定端,柔性铰链c所在的位置处为位移输入端,柔性铰链b所在位置为位移输出端。工作状态下,输入端输入位移Δu,由于端点q处于约束状态,输出端输出位移Δv,从而实现输入位移缩小。
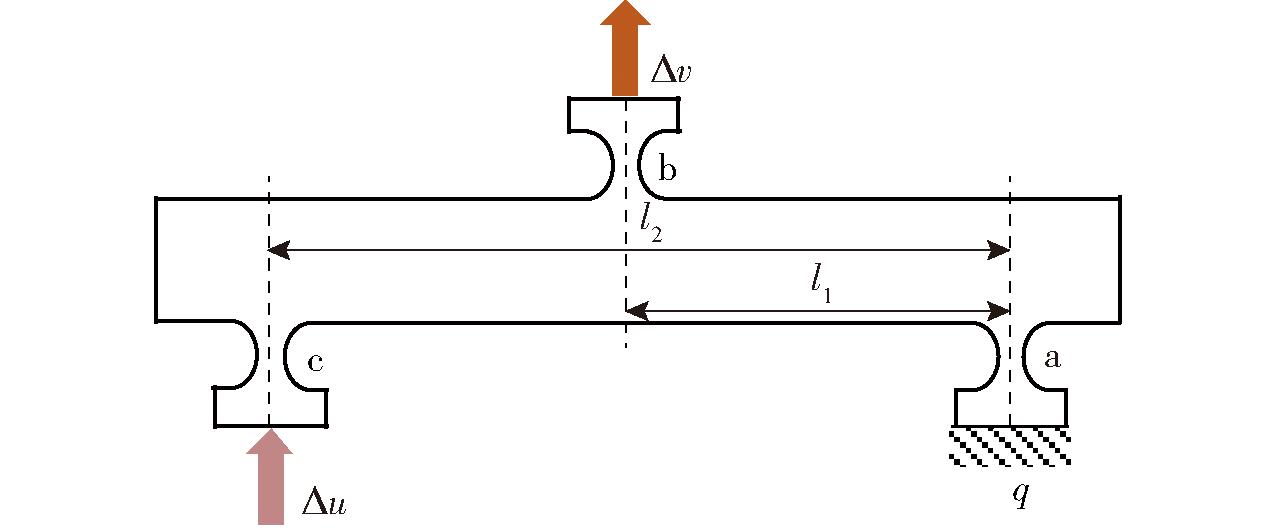
图2 杠杆原理图
Fig.2 Lever principle diagram
图3为杠杆缩小比计算模型,设杠杆转角为φ,则柔性铰链转角αi和杆件转角φ之间存在关系
α2=α6=φ
(1)
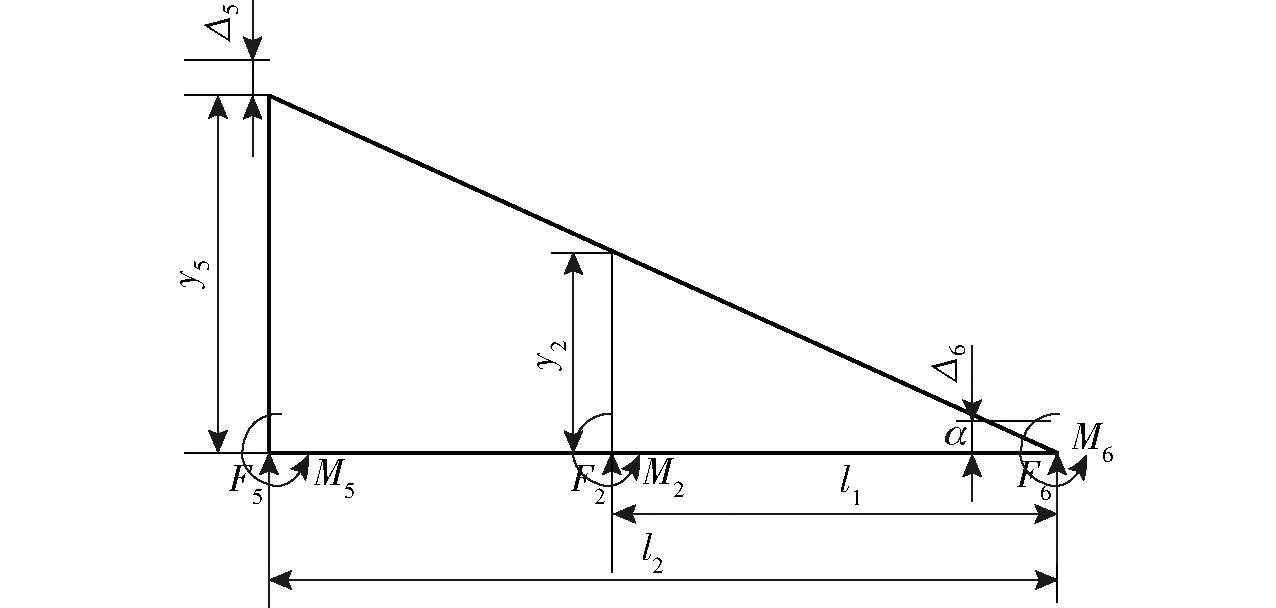
图3 缩小比计算模型
Fig.3 Reduction ratio calculation model
式中 αi——柔性组件i转角
如图3所示,通过分析杠杆受力以及输入、输出位移情况,根据力平衡条件,可得
F5=F2+F6
(2)
F2l1+M5+M6=F5l2+M2
(3)
式中 Fi——柔性铰链i受到的力
Mi——柔性铰链i受到的力矩
杠杆以柔性铰链6为转动中心,柔性铰链6在拉力F6的作用,轴向伸长量为Δ6,柔性铰链5在输入力作用下,轴向受压,压缩量为Δ5,则有
x5=x-Δ5
(4)
式中 x——负载条件下杠杆输出位移
x5——杠杆输入端输入位移
由于θ较小,杠杆转角θ为
(5)
式中 x2——杠杆输出端输出位移
根据式(1)~(5)得杠杆理论缩小倍数为
(6)
因此,通过调整微动缩小机构设计参数,可实现不同缩小比,从而适用于不同工程应用。
无附加运动原理如图4所示,中间位置放置微驱动器(PZT),6个柔性组件对称分布在PZT两侧。
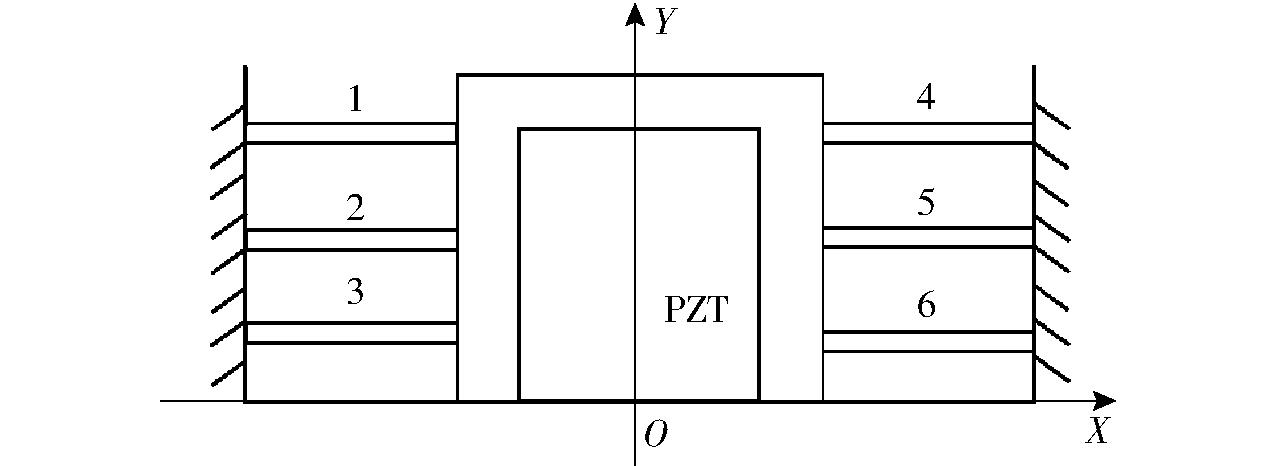
图4 无附加运动原理图
Fig.4 Principle of unattached motion
在沿Y轴运动过程中,柔性组件1、2、3和柔性组件4、5、6不仅会产生运动方向(Y方向)的力和位移,还会在非运动方向(X方向)产生力和位移。柔性组件1、2、3、4、5、6对称地放置于微驱动器两侧,这些组件在运动中产生的交叉耦合力和位移被有效平衡,使得精密微动缩小机构仅沿Y方向运动,而不会产生非运动方向(X方向)的力和位移。
基于柔性铰链杠杆原理和无附加运动原理,设计一种精密微动缩小机构(设计缩小比为2∶1),如图5所示,机构由输入部分A、连接部分B、缩小部分C和输出部分D 4部分构成,X轴、Y轴、Z轴的方向尺寸为150 mm×128 mm×50 mm,共有12个柔性组件,柔性组件中各柔性铰链尺寸如图5所示。
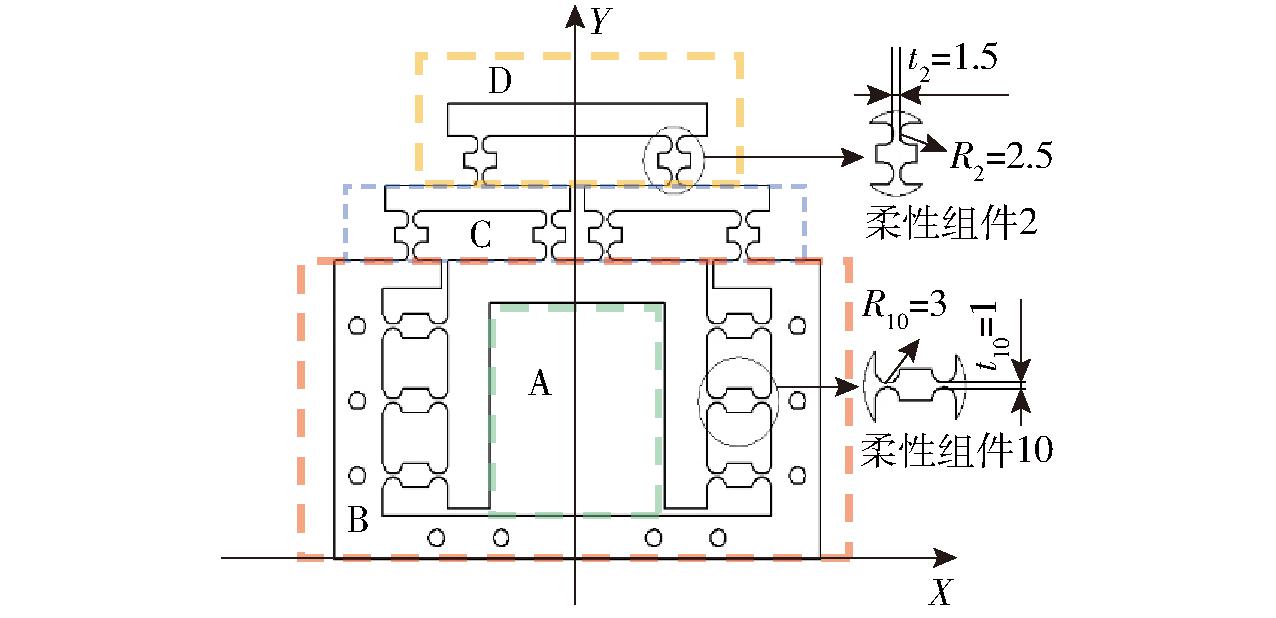
图5 精密微动缩小机构结构图
Fig.5 Precision micromotion narrowing mechanism structure diagram
输入部分A:精密微动缩小机构需依靠微驱动器驱动来提供输入,因此需给微驱动器预留足够位置。设计中间方形孔位用于安装微驱动器,方形孔位基本尺寸定为微驱动器尺寸。
连接部分B:机构左右对称设计6个铰链组件,以确保机构在工作时无附加力及位移产生。两侧以及底端对称设计10个螺纹孔,方便与其他机构进行装配。
缩小部分C:对机构进行调整可得不同缩小比精密微动缩小机构,以缩小比为2∶1设计精密微动缩小机构。
输出部分D:输出部分通过2个柔性组件,将缩小部分杠杆变化所产生的输出位移进行精密输出。
选择精密微动缩小机构材料时,综合各种材料弹性模量、硬度、强度和疲劳强度等性能以及材料成本、实用价值等方面,采用60Si2Mn作为精密缩小机构加工材料,材料属性如表1所示。采用线切割技术对精密微动缩小机构进行加工,以满足精密微动缩小机构在加工精度和复杂形状等方面的需求。
表1 60Si2Mn材料属性
Tab.1 Material properties of 60Si2Mn

参数杨氏模量/MPa屈服极限/MPa抗拉强度/MPa泊松比密度/(g·cm-3)数值2.06×105117612740.297.74
为验证所设计的微动缩小机构无附加运动性能,采用有限元法对其进行运动学分析。首先,对精密微动缩小机构整体选用质量中、2 mm的单位四面体网格进行划分;然后,对其26个柔性铰链使用Refinement参数为2进行网格单元细化。柔性铰链最薄弱处圆弧截面,采用0.5 mm为单元进行局部网格细化。网格划分结果如图6所示,模型共划分为1 293 474个单元、762 841个节点。

图6 网格划分结果
Fig.6 Grid division results
对微动缩小机构上的10个螺栓孔施加固定约束,如图7中蓝色部分B所示;并在精密微动缩小机构输入面上施加输入位移Δu=2 μm,如图7中黄色部分A所示。
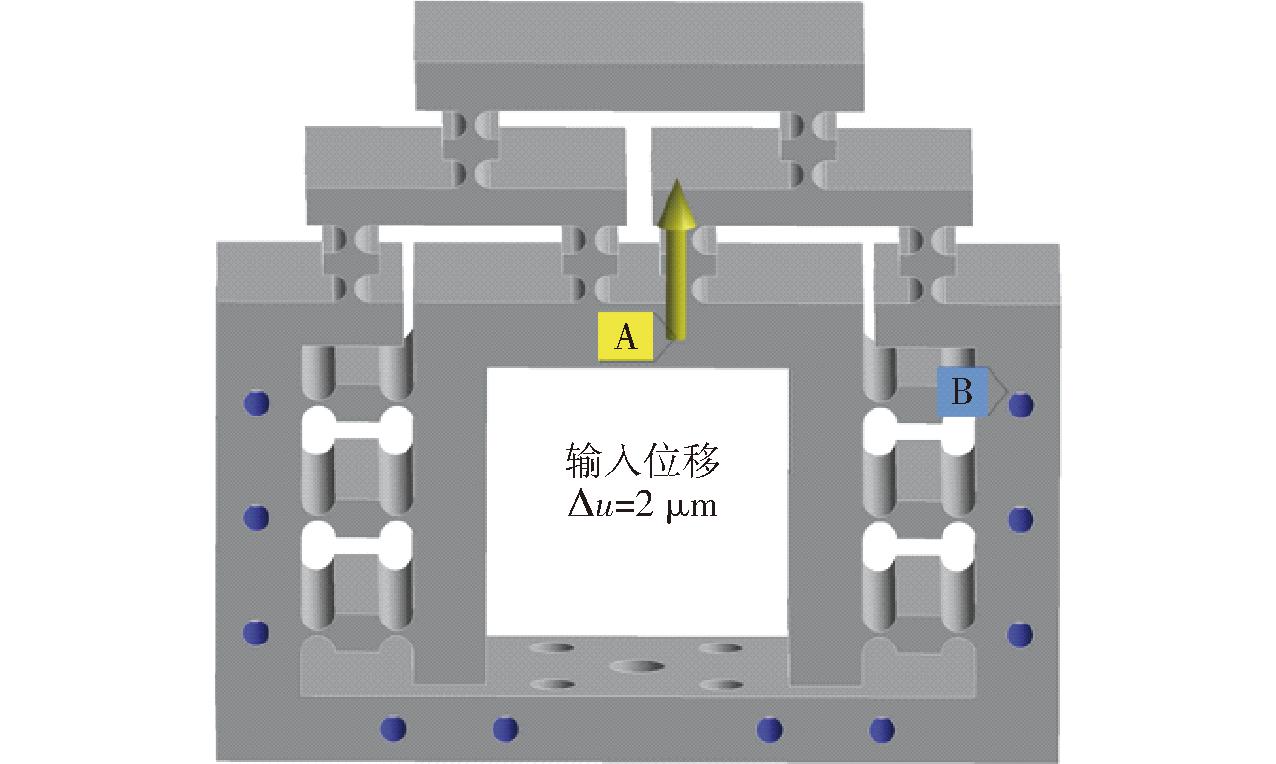
图7 施加固定约束与位移
Fig.7 Applying fixed constraints and displacements
对精密微动缩小机构采用探针功能检测分别施加输入位移2、4、6、8、10 μm时Y方向输出位移、X方向输出位移以及X方向输出力,在施加输入位移2 μm时,图8表明Y方向输出位移为0.905 3 μm和X方向输出位移为1.1×10-4 μm,图9表明X方向输出力为0。
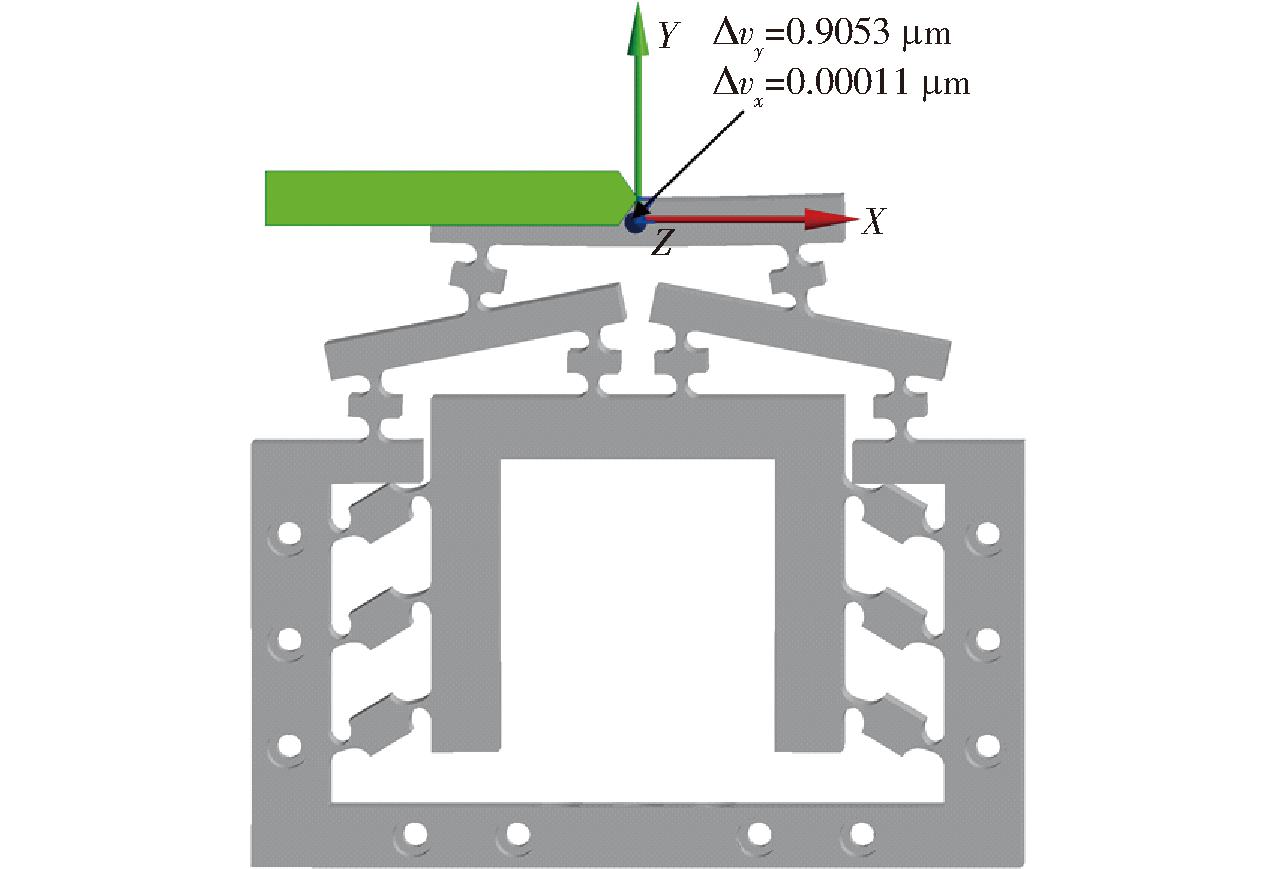
图8 输入位移为2 μm时Y方向及X方向位移
Fig.8 Y-direction and X-direction displacements at input displacement of 2 μm
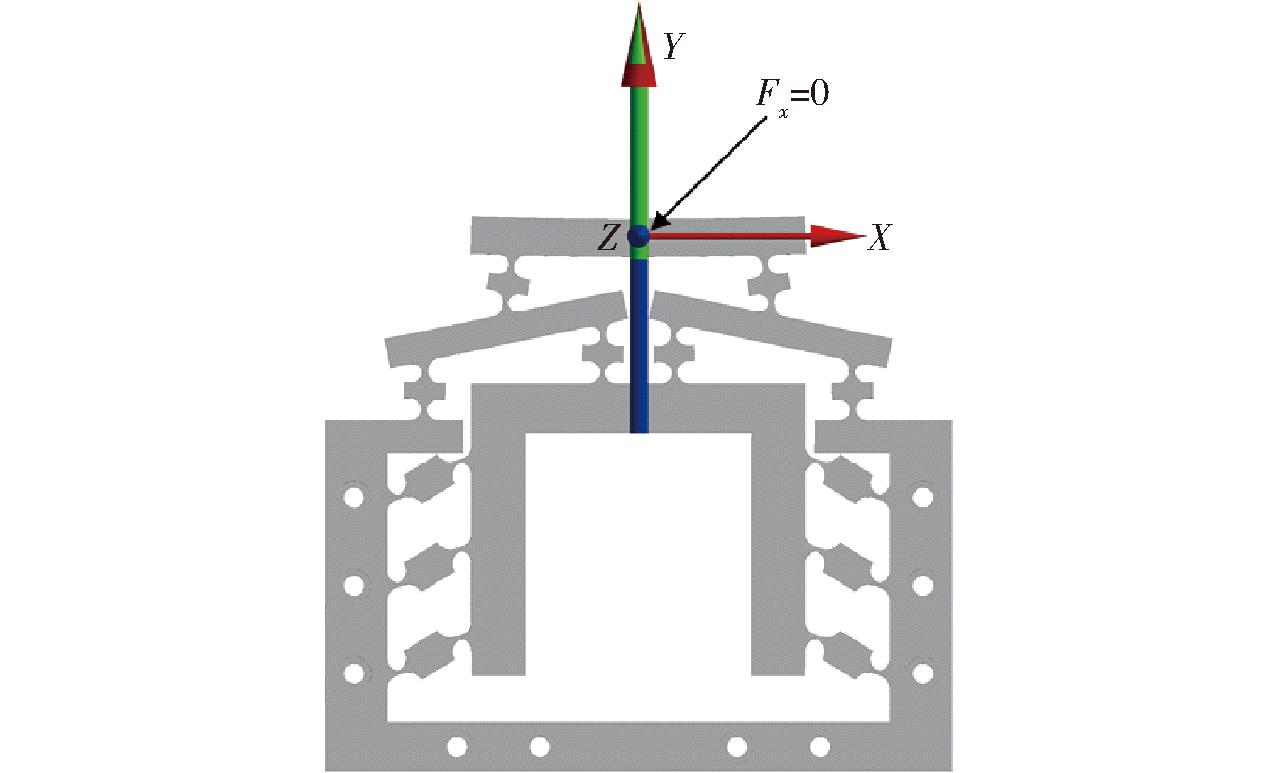
图9 输入位移为2 μm时X方向的力
Fig.9 X-direction force at input displacement of 2 μm
如表2所示,非运动方向X方向输出位移与运动方向Y方向输出位移最大误差为0.011 5%,且X方向输出力为零。表明该机构具有良好的输出精度,并且在非运动方向上没有力和位移,从而验证了其在运动过程中无附加运动特性。
表2 无附加运动性能
Tab.2 No additional motion performance
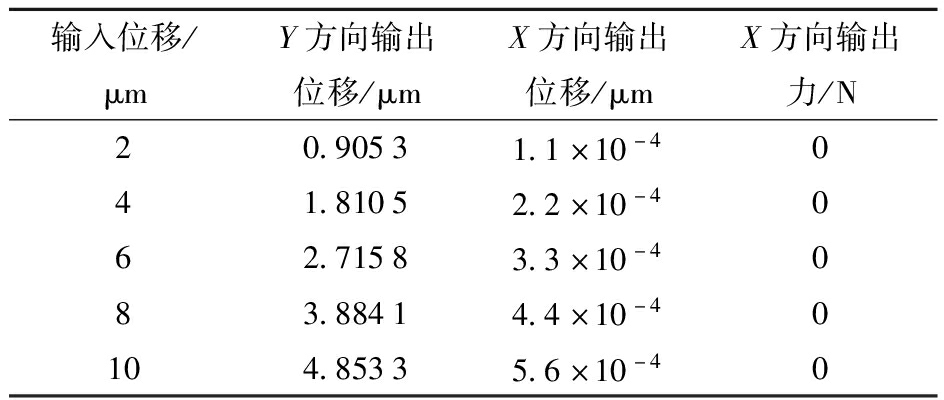
输入位移/μmY方向输出位移/μmX方向输出位移/μmX方向输出力/N20.90531.1×10-4041.81052.2×10-4062.71583.3×10-4083.88414.4×10-40104.85335.6×10-40
等效刚度法通过将复杂结构刚度特性转换为相对简单的等效模型,实现了对系统刚度特性的准确描述。这种方法在不损失分析精度的同时,大幅度提高了计算效率。它克服了其他刚度分析方法在处理复杂微动机构时存在力学分析复杂和数学计算量大的不足。
由于本文设计的精密微动机构结构复杂,需一种既能简化力学分析和数学计算,又能保证系统整体刚度特性准确描述的方法。因此,采用等效刚度法对精密微动缩小机构进行刚度分析。
如图10所示,从图示位置O处施加输入位移y,将柔性组件1~12所示(12个柔性组件结构相同,都由2个柔性铰链和1个杆件串联组成)看作柔性件,精密微动缩小机构其余部分则作为刚性件处理。
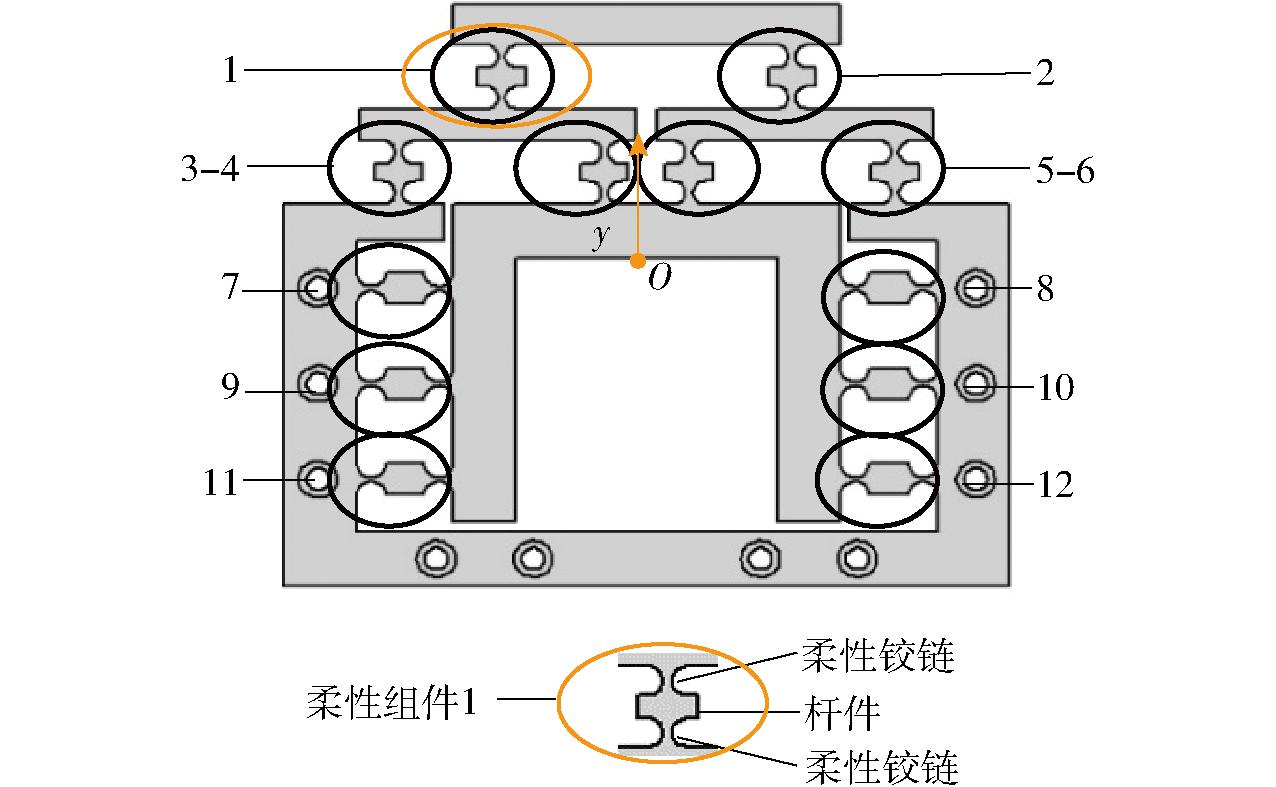
图10 精密微动缩小机构上的铰链单元分布
Fig.10 Distribution of hinge units on precision micromotion reduction mechanism
每一个柔性组件都看作一个理想运动副,因此整个精密微动缩小机构势能为
(7)
式中 Ki——柔性组件i刚度
θi——柔性组件转过角
柔性组件1由2个柔性铰链和1个杆件组成,并且三者之间为串联关系,因此柔性组件1刚度与组成它的2个柔性铰链和1个杆件刚度关系为
(8)
(9)
(10)
f1=fA1+fB1
(11)
(12)
(13)
S1=R1/t1
(14)
式中 K1——柔性组件1刚度
K1a——柔性组件1中柔性铰链刚度
K1b——柔性组件1中杆件刚度
E——精密微动缩小机构材料弹性模量
b1——柔性组件1中柔性铰链宽度
R1——柔性组件1中柔性铰链半径
t1——柔性组件1中柔性铰链厚度最小值
h1——柔性组件1中杆件高度
d1——柔性组件1中杆件长度
由式(8)~(14)得柔性组件1刚度为
(15)
柔性组件7由2个柔性铰链和1个杆件组成,并且三者之间为串联关系,类比上述柔性组件1的计算方法,f7计算方法类比于f1,得柔性组件7刚度
(16)
如图10所示,柔性组件1到柔性组件6中的柔性组件相同,柔性组件7到柔性组件12中的柔性组件相同,即
(17)
O处施加输入位移y为微米级别,因此各个柔性组件转过角度非常小,则柔性组件i转过角θi可以近似为tanθi,因此
(18)
式中 Li——柔性组件i到点O的垂直距离
柔性组件1和柔性组件2对称分布,可得
L1=L2
(19)
由式(18)、(19)得
θ1=θ2
(20)
同理
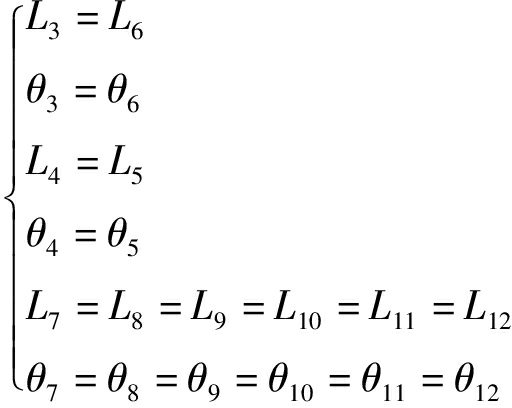
(21)
对式(7)~(21)进行整理,得
(22)
即微动缩小机构等效刚度
(23)
将R1=2.5 mm、t1=1.5 mm、b1=50 mm、d1=10 mm、h1=4 mm、R7=3 mm、t7=1 mm、b7=50 mm、d7=8 mm、h7=7 mm、E=2.06×105 MPa、L1=25 mm、L3=4.38 mm、L5=45.62 m、L7=40 mm代入式(15)、(16)、(23),得出精密微动缩小机构等效刚度为K为75.72 N/μm。
为验证所建立的等效刚度法理论的正确性,采用有限元法对该机构进行了详细的刚度分析。本部分有限元分析前期处理与本文1.5节中所述一致。为了加强模型稳定性,微动缩小机构上10个螺栓孔施加固定约束,如图11中蓝色部分B所示;并在精密微动缩小机构输入面上施加100 N力,如图11中红色部分A所示。
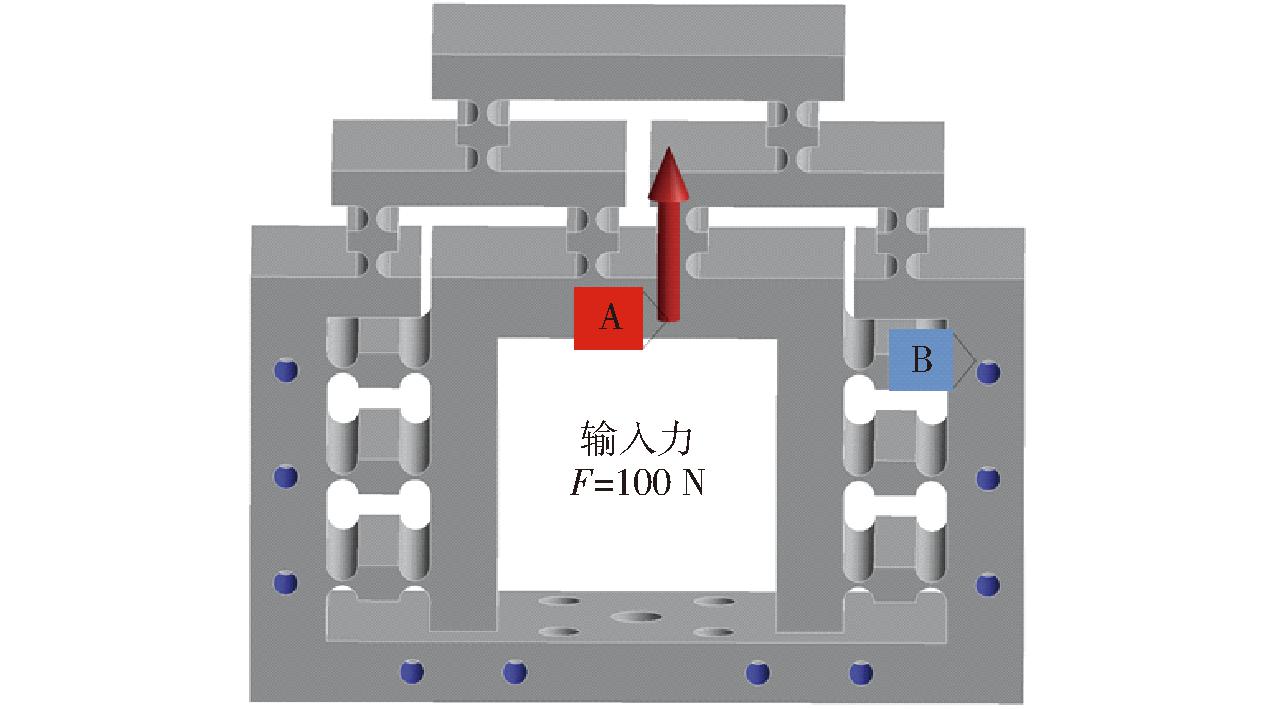
图11 施加固定约束与力
Fig.11 Applying fixed constraints and force
在微动缩小机构输出处插入变形探针,以便检测施加不同载荷时机构输出处变形量。图12为在精密微动缩小机构输入面上施加100 N载荷时,探针检测到其输入位移为1.35 μm。
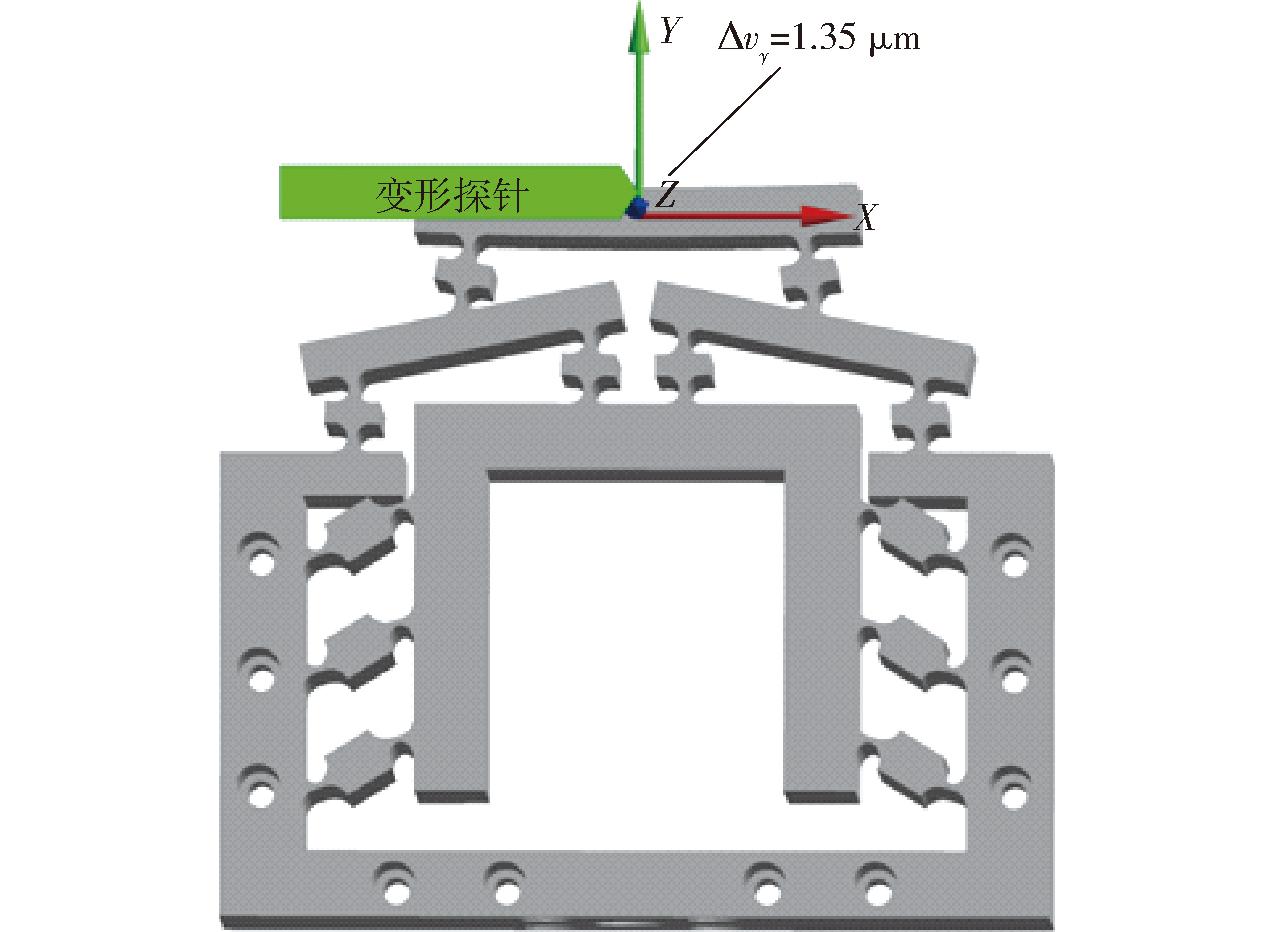
图12 机构施加100 N载荷时的输出位移
Fig.12 Output displacement when 100 N load was applied to mechanism
对精密微动缩小机构施加载荷100、200、300、400、500 N,记录其输出位移,并计算出其不同载荷下刚度。有限元分析结果如表3所示。
表3 有限元分析结果
Tab.3 Finite element analysis results
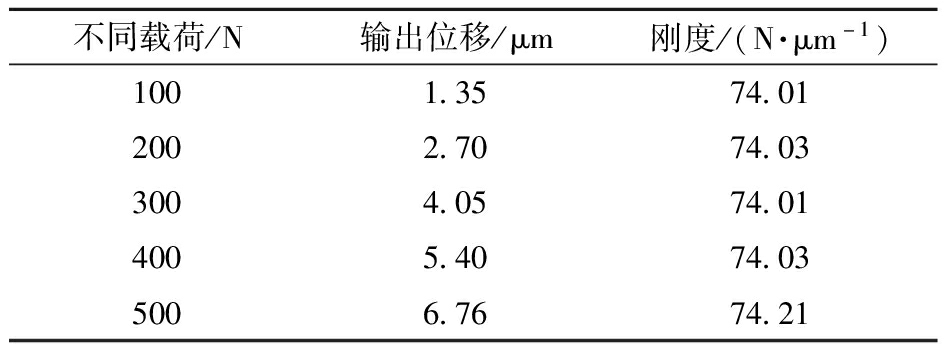
不同载荷/N输出位移/μm刚度/(N·μm-1)1001.3574.012002.7074.033004.0574.014005.4074.035006.7674.21
通过对有限元分析结果求平均值,得到其精密微动缩小机构刚度为74.06 N/μm。有限元分析结果与理论分析结果最大误差为2.26%,最小误差为2.00%。虽然有限元分析中刚度普遍低于理论值,但误差范围较小,证明了所建立的等效刚度法理论在实际应用中的有效性和可靠性。
为进一步验证理论分析结果和仿真结果,采用实验室条件对精密微动缩小机构刚度性能进行实验。实验采用直式电感式传感器(2个)、精密微动缩小机构、压电陶瓷致动器(P235.1s型)、磁力表座、实验底座等装置,实验装置如图13所示。

图13 刚度实验装置
Fig.13 Stiffness experiment diagram
1.一号传感器 2.二号传感器 3.精密微动缩小机构 4.压电陶瓷致动器 5.磁力表座 6.实验底座
通过压电陶瓷致动器为精密微动机构提供输入载荷,在输入载荷作用下,精密微动缩小机构产生输出位移,输出位移采用电感式直线位移传感器测量。给精密微动缩小机构依次施加载荷100、200、300、400、500 N,记录不同载荷下平台输出位移,并计算刚度。精密微动缩小机构在施加不同载荷情况下,其理论分析结果、有限元分析结果与实验结果对比如表4所示。得刚度平均值为68.86 N/μm。
表4 理论分析、有限元分析与实验结果对比
Tab.4 Comparison of theoretical analysis,finite element analysis and experimental results

施加载荷/N有限元分析输出位移/μm实验输出位移/μm理论分析刚度/(N·μm-1)有限元分析刚度/(N·μm-1)实验刚度/(N·μm-1)1001.351.4575.7274.0168.872002.702.9075.7274.0368.843004.054.3575.7274.0168.874005.405.8075.7274.0368.865006.767.2575.7274.2169.86
将有限元分析结果与实验结果分别进行线性拟合,并与理论分析结果绘制在同一坐标系中,结果如图14所示。
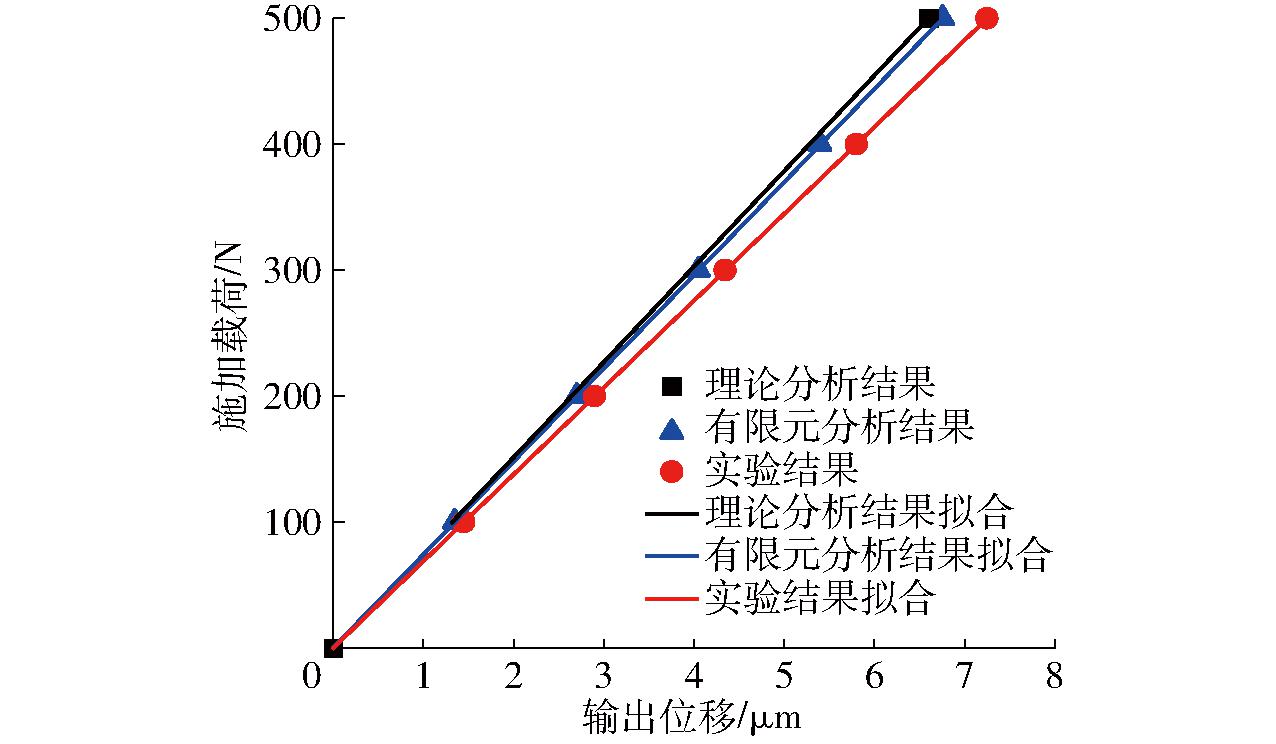
图14 精密微动平台刚度线性拟合
Fig.14 Stiffness linear fitting of precision micromanipulator stages
对理论分析结果进行拟合,得到拟合方程为
y=75.72x
(24)
对有限元分析结果进行拟合,得到拟合方程为
y=73.964x+0.297
(25)
对实验结果进行拟合,得到拟合方式为
y=75.42x-0.000 000 541
(26)
比较有限元分析、理论分析和实验结果,可得三者之间存在一定差异。理论分析刚度为75.72 N/μm,有限元分析刚度平均值为74.06 N/μm,实验结果刚度平均值为68.86 N/μm。理论分析与有限元分析结果误差为2.19%,而理论分析与实验结果误差为9.06%。
上述研究结果验证了精密微动缩小机构理论刚度分析方法的有效性和正确性。
(1)基于柔性铰链杠杆原理和无附加运动原理设计了一种精密微动缩小机构,该机构能够将输入位移按照比例2∶1精确缩小,同时避免非运动方向的力和位移的产生,从而确保精密微动缩小机构运动过程中的安全性及精密性。
(2)采用等效刚度法对精密微动缩小机构进行了刚度分析,并采用有限元法及实验法进行了验证,结果表明:理论分析与有限元分析误差2.19%,理论分析与实验结果误差为9.06%。研究结果验证了等效刚度法的有效性和精确性,对精密微动机构刚度分析具有重要的参考价值。
[1] DATTA M.Manufacturing processes for fabrication of flip-chip micro-bumps used in microelectronic packaging:an overview[J].Journal of Micromanufacturing,2020,3(1):69-83.
[2] AXINTE D,HUANG H,YAN J,et al.What micro-mechanical testing can reveal about machining processes[J].International Journal of Machine Tools and Manufacture,2022,183:103964.
[3] HUANG X,QI Y,BU T,et al.Overview of advanced micro-nano manufacturing technologies for triboelectric nanogenerators[J].Nanoenergy Advances,2022,2(4):316-343.
[4] ZHANG L,ZHANG P,JIANG B,et al.Research trends in methods for controlling macro-micro motion platforms[J].Nanotechnology and Precision Engineering,2023,6(3):64-78.
[5] ZHANG S,ZHANG T,MENG F.Development of a 3-DOF flexible micro-motion platform based on a symmetrical two-stage magnifying mechanism[J].Engineering Research Express,2023,5(3):035012.
[6] RAUT P P,RAO A S,SOLLAPUR S,et al.Investigation on the development and building of a voice coil actuator-driven XY micro-motion stage with dual-range capabilities[J].International Journal on Interactive Design and Manufacturing (IJIDeM),2024,18(7):4397-4408.
[7] YU C,CHENG Z,XIONG M,et al.Magnetic field model of macro-motion of coaxial integrated macro-micro composite actuator[J].Journal of Magnetics,2021,26(1):79-86.
[8] 唐皓,张贺,张栋,等.基于微动特性分析的精密线性平台微行程重复定位精度表征与补偿[J].机械工程学报,2023,59(21):110-120.TANG Hao,ZHANG He,ZHANG Dong,et al.Characterization and compensation of microstroke repetitive positioning accuracy of a precision linear stage based on micromotion characterization[J].Journal of Mechanical Engineering,2023,59(21):110-120.(in Chinese)
[9] ZHANG L,GAO J.Implementation and experiment of a novel piezoelectric-spring stage for rapid high-precision micromotion[J].Microsystem Technologies,2021,27:2943-2954.
[10] 张宪民,朱本亮,李海,等.柔顺精密定位与操作机构研究进展[J].机械工程学报,2023,59(19):24-43.ZHANG Xianmin,ZHU Benliang,LI Hai,et al.Research progress on flexible precision positioning and operating mechanism[J].Journal of Mechanical Engineering,2023,59(19):24-43.(in Chinese)
[11] 秦宇,冯之敬.纳米级定位精度弹性位移缩小机构的仿真与实验[J].纳米技术与精密工程,2007,5(1):19-22.QIN Yu,FENG Zhijing.Simulation and experiment of elastic displacement reduction mechanism with nanoscale positioning accuracy[J].Nanotechnology and Precision Engineering,2007,5(1):19-22.(in Chinese)
[12] HAYASHI M,FUKUDA M.Generation of nanometer displacement using reduction mechanism consisting of torsional leaf spring hinges[J].International Journal of Precision Engineering and Manufacturing,2012,13:679-684.
[13] FUKUDA M,HAYASHI M,MARITA S.Generating sub-nanometer displacement using reduction mechanism consisting of torsional leaf spring hinges[J].Measurement Science Review,2014,14(1):48-51.
[14] ZHANG L,GAO J.A novel rapid micromotion compensator for high-precision chip bonding manufacturing[J].Precision Engineering,2021,71:282-292.
[15] FUNARI M F,SILVA L C,SAVALLE N,et al.A concurrent micro/macro FE-model optimized with a limit analysis tool for the assessment of dry-joint masonry structures[J].International Journal for Multiscale Computational Engineering,2022,20(5):65-85.
[16] 孙驰宇,沈惠平,王一熙,等.零耦合度部分运动解耦三平移并联机构刚度建模与分析[J].农业机械学报,2020,51(6):385-395.SUN Chiyu,SHEN Huiping,WANG Yixi,et al.Stiffness modeling and analysis of zero-coupling partial motion decoupled triple translational parallel mechanism[J].Transactions of the Chinese Society for Agricultural Machinery,2020,51(6):385-395.(in Chinese)
[17] 王永立,路懿.分流式柔性铰六维力传感器刚度分析与结构优化[J].农业机械学报,2019,50(6):419-426.WANG Yongli,LU Yi.Stiffness analysis and structural optimization of manifold flexible hinged six-dimensional force sensor[J].Transactions of the Chinese Society for Agricultural Machinery,2019,50(6):419-426.(in Chinese)
[18] 郑洋洋,宫金良,张彦斐.基于传递矩阵法的柔性杠杆放大机构刚度分析[J].北京航空航天大学学报,2017,43(4):849-856.ZHENG Yangyang,GONG Jinliang,ZHANG Yanfei.Stiffness analysis of flexible lever amplification mechanism based on transfer matrix method[J].Journal of Beijing University of Aeronautics and Astronautics,2017,43(4):849-856.(in Chinese)
[19] 于靖军,毕树生,宗光华.空间全柔性机构位置分析的刚度矩阵法[J].北京航空航天大学学报,2002,28(3):323-326.YU Jingjun,BI Shusheng,ZONG Guanghua.Stiffness matrix method for position analysis of spatially fully flexible mechanisms[J].Journal of Beijing University of Aeronautics and Astronautics,2002,28(3):323-326.(in Chinese)
[20] WU Z,LI Y,HU M.Design and optimization of full decoupled micro/nano-positioning stage based on mathematical calculation[J].Mechanical Sciences,2018,9(2):417-429.
[21] 杨满芝,李林岳,张传伟,等.基于平衡附加力原理的微动放大机构设计与实验[J].农业机械学报,2022,53(12):452-458.YANG Manzhi,LI Linyue,ZHANG Chuanwei,et al.Design and experiment of micro-amplification mechanism based on the principle of balanced additional force[J].Transactions of the Chinese Society for Agricultural Machinery,2022,53(12):452-458.(in Chinese)
[22] YU Y,GAO Q,QIAO G,et al.A direction-guidance hybrid excitation method for inertial flexible hinge piezoelectric actuator with high speed performance[J].Sensors and Actuators A:Physical,2020,314:112229.
[23] 马金玉,余胜东,康升征,等.基于压电作动器驱动的微操作机构设计与运动控制[J].农业机械学报,2021,52(9):417-426.MA Jinyu,YU Shengdong,KANG Shengzheng,et al.Design and motion control of micromanipulator based on piezoelectric actuator drive[J].Transactions of the Chinese Society for Agricultural Machinery,2021,52(9):417-426.(in Chinese)
[24] 李宗轩,张雷,姚劲松,等.Cartwheel型双轴柔性铰链设计[J].光学精密工程,2013,21(9):2317-2325.LI Zongxuan,ZHANG Lei,YAO Jinsong,et al.Design of Cartwheel-type biaxial flexible hinge[J].Optical Precision Engineering,2013,21(9):2317-2325.(in Chinese)
[25] 李冲,童玉健,梁康,等.压电驱动微型精密夹持机构设计与实验研究[J].中国机械工程,2022,33(11):1302-1308,1385.LI Chong,TONG Yujian,LIANG Kang,et al.Design and experimental study of piezoelectric-driven micro-precision clamping mechanism[J].China Mechanical Engineering,2022,33(11):1302-1308,1385.(in Chinese)
[26] 李耀,吴洪涛,杨小龙,等.圆弧柔性铰链的优化设计[J].光学精密工程,2018,26(6):1370-1379.LI Yao,WU Hongtao,YANG Xiaolong,et al.Optimized design of circular arc flexible hinge[J].Optical Precision Engineering,2018,26(6):1370-1379.(in Chinese)