OSID：
随着现代农业的快速发展,温室精准定位技术日益受到重视。尽管传统的全球导航卫星系统(Global navigation satellite system,GNSS)在室外定位领域占据主导地位[1-4],但其在温室环境中的应用受限于多路径效应[5-6]和非视距影响[7-8],这些因素严重制约了定位精度和可靠性[9]。因此,探索替代GNSS的室内定位技术尤为迫切。
UWB技术以其高精度、低功耗和出色的安全性[10],在智慧城市[11-12]、智能交通[13-14]及精细农业[15-16]等多个领域得到广泛应用,现已成为温室定位技术的新选择[17-19]。然而,UWB技术在室内环境中面临诸多挑战,尤其是多径效应,它会导致信号衰落和时间延迟,影响定位精度[20-22]。为应对这一问题,HE等[23]提出了一种基于注意力机制的UWB测距误差补偿算法,通过优化深度神经网络模型,有效减少了多路径效应对测距精度的负面影响。但该算法对不同环境的变化较为敏感,在极端复杂或动态环境下效果不佳。ZHANG等[24]开发了一种低成本的UWB-里程计融合方法,利用动态窗口粒子滤波器实现了移动机器人定位。该方法不仅克服了里程计累计误差带来的影响,而且有效提高了粒子的收敛,降低了硬件成本,但在信号丢失或干扰情况下,单个UWB锚点的依赖会导致系统性能下降。ZABALEGUI等[25]采用了故障检测与排除(Fault detection exclusion,FDE)技术,旨在应用UWB技术进行室内或城市环境定位时使用故障锚点。在上述环境中,该方法增强了UWB抗多径效应影响的能力。然而,在温室环境中,由于存在各种电气和无线通信设备,可能会导致信号质量下降,从而增加FDE方法在检测和排除故障信号时的难度。
除了多径效应,UWB定位系统受NLOS的影响也不容忽视[26-27]。PAN等[28]提出一种基于室内场景的UWB锚点优化方法,通过室内建模和组合测距模型,结合差分进化算法最小化误差,实现了分米级定位精度。然而,该方法计算复杂度较高,可能会导致延迟,影响实时性。LIU等[29]提出了一种结合卷积神经网络(Convolutional neural networks,CNN)和平行门控循环单元(Gate recurrent unit,GRU)的室内LOS/NLOS识别神经网络,但该方法解决了不同室内环境中UWB的NLOS/LOS识别问题。该方法对计算能力和存储资源的要求较高,这在资源有限的农业设备中可能受到限制。CHEN等[30]提出了一种结合圆极化天线、遗传算法和机器学习的UWB系统,用于室内定位,优化锚点位置并减小NLOS误差,实现高定位精度。然而,应用于温室时,会受到温室环境的动态变化等影响。
为提高导航系统的定位精度,研究人员提出了多种异常检测机制。胡晓强等[31]提出了一种组合导航系统复合型异常检测与容错算法,目的是解决组合导航系统在外部干扰情况下导航精度下降的问题。STAHLKE等[32]提出一种基于变分自编码器(Variational auto-encoder,VAE)的异常检测方法,提升了UWB系统的定位精度。然而,由于温室中大量金属结构、植被等物体的存在,UWB信号在传输过程中容易受到干扰或遮挡,从而导致异常检测机制的有效性降低。
上述研究为提高不同场景下的UWB定位精度提供了方法。但温室环境复杂,同时,注重经济成本与定位精度的平衡,对用于农用车辆的UWB定位系统提出更高的要求。因此,针对温室环境中UWB定位面临的测量噪声动态变化问题,本文提出一种IAKF算法,集成量测异常检测处理和自适应滤波技术,有效识别和降低异常值的影响,并动态调整滤波参数,适应噪声变化性较大的环境。
以农用履带车辆为试验对象。假设k时刻为当前时刻,定义系统的状态向量为
(1)
式中 Xk——k时刻车辆状态向量
xk——k时刻车辆在x轴方向上位置,m
yk——k时刻车辆在y轴方向上位置,m
vx,k——k时刻车辆在x方向速度,m/s
vy,k——k时刻车辆y方向速度,m/s
则状态方程为
Xk=FXk-1+Wk
(2)
其中
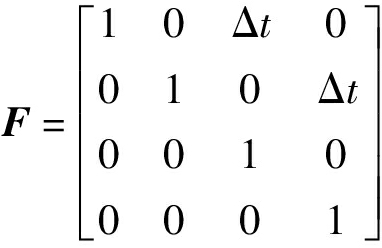
(3)
E(Wk)=qk
(4)
Var(Wk)=QK
(5)
式中 F——状态转移矩阵
Xk-1——k-1时刻系统状态
Wk——k时刻系统噪声矩阵
Δt——UWB采样间隔
qk——k时刻系统噪声Wk期望值
QK——k时刻系统噪声Wk方差
Var()——方差运算
E()——期望运算
定义k时刻系统观测方程为
Zk=HXk+Vk
(6)
其中
E(Vk)=rk
(7)
Var(Vk)=Rk
(8)
式中 Zk——k时刻车辆观测向量
H——观测矩阵
Vk——k时刻观测噪声矩阵
rk——k时刻观测噪声Vk期望值
Rk——k时刻观测噪声Vk方差
Wk和Vk为时序统计特性系统噪声矩阵。
UWB基站和标签布局如图1所示。在k时刻,A、B、C、D 4个基站对标签O进行测距,则基站与标签之间距离计算式为
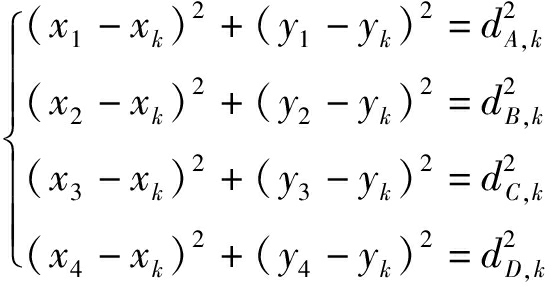
(9)
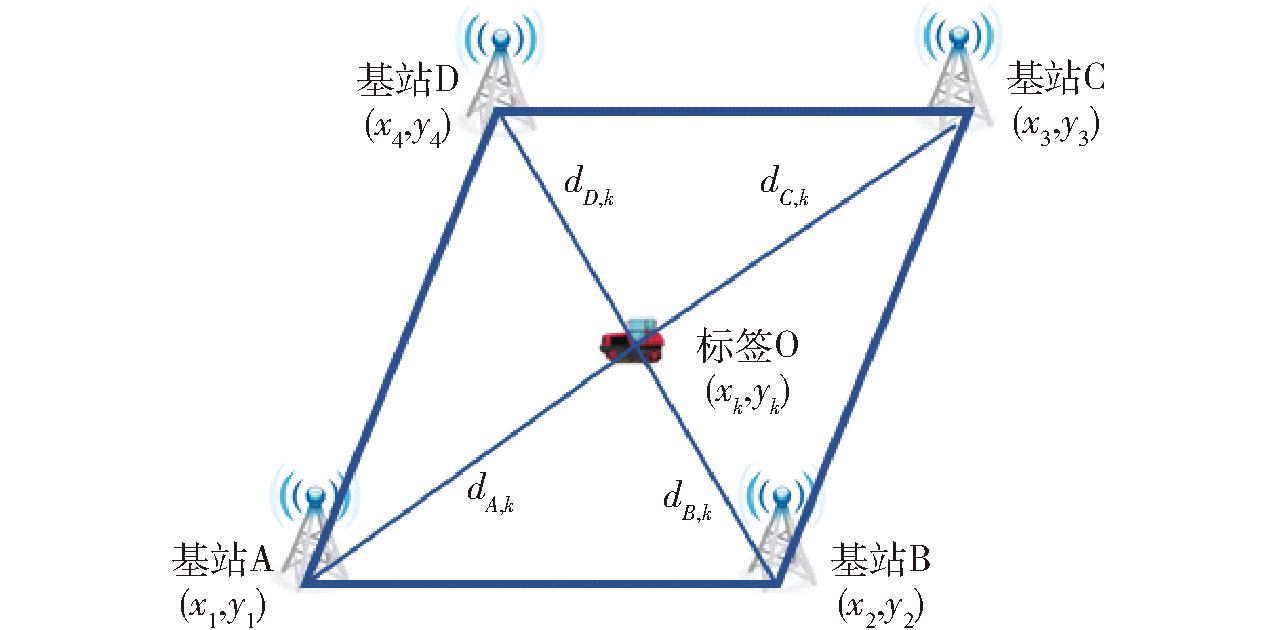
图1 UWB定位原理图
Fig.1 UWB positioning principle
式中 dA,k——k时刻基站A对标签O测距距离,m
dB,k——k时刻基站B对标签O测距距离,m
dC,k——k时刻基站C对标签O测距距离,m
dD,k——k时刻基站D对标签O测距距离,m
i——基站序号,i=1,2,3,4,对应A、B、C、D
(xi,yi)——基站坐标
(xk,yk)——k时刻标签坐标
对式(9)中的完全平方差项进行展开
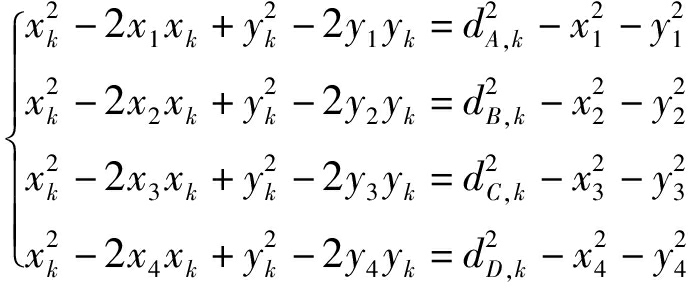
(10)
由于标签坐标包含无法直接解算的高阶项,因此通过对方程进行三次差分来消除这些高阶项。经过差分处理后,可简化为
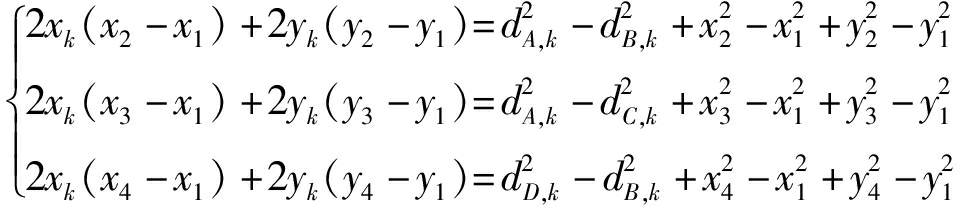
(11)
将式(11)中的方程转换为矩阵形式得
Ak=BkXTag,k
(12)
其中
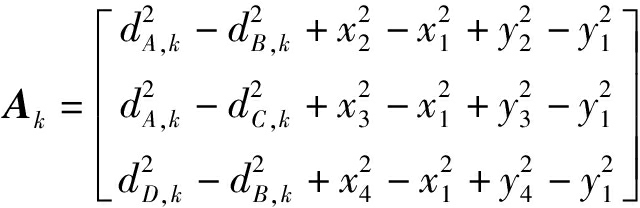
(13)
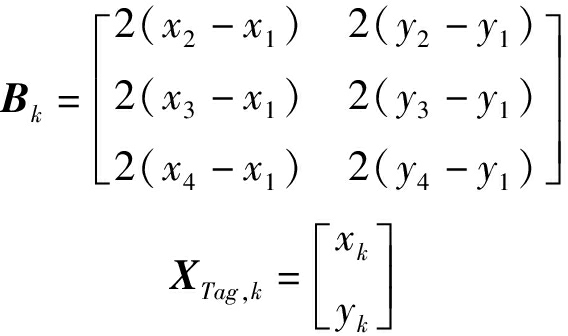
(14)
式中 XTag,k——所求的标签坐标
自适应卡尔曼滤波融合了经典卡尔曼滤波和噪声估计技术,实现对系统和观测误差统计特性实时更新。该算法在滤波过程中根据环境变换动态调整噪声参数,在应对系统和观测噪声随时间变化的场景尤为合适,有效提升对系统状态估计精度。自适应卡尔曼滤波算法表达式为[33]
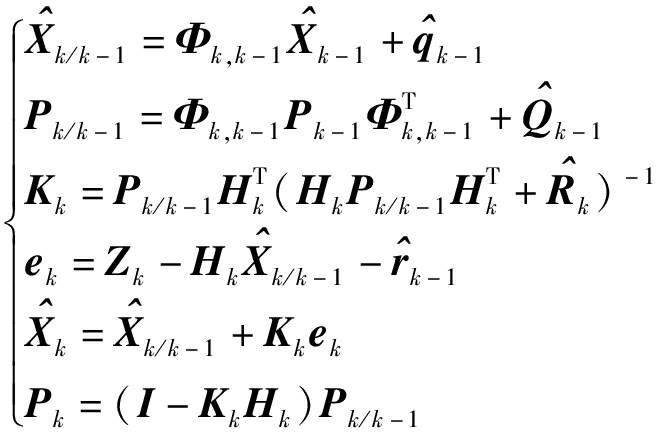
(15)
式中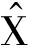 
k/k-1——k时刻预测状态向量
Φk,k-1——k-1时刻到k时刻状态转移矩阵
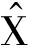k-1——k-1时刻估计状态向量
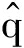k-1——k-1时刻过程噪声的期望值
Pk/k-1——k时刻预测状态协方差矩阵
Pk-1——k-1时刻估计状态协方差矩阵
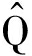k-1——k-1时刻过程噪声协方差矩阵
Kk——k时刻卡尔曼增益矩阵
Hk——k时刻观测矩阵
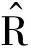k——k时刻测量噪声协方差矩阵
ek——k时刻新息向量 I——单位矩阵
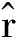k-1——k-1时刻测量噪声的期望值
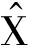k——k时刻估计状态向量
Pk——k时刻估计状态协方差矩阵
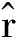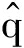对k-1、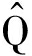k-1、k-1、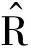k进行更新,公式为
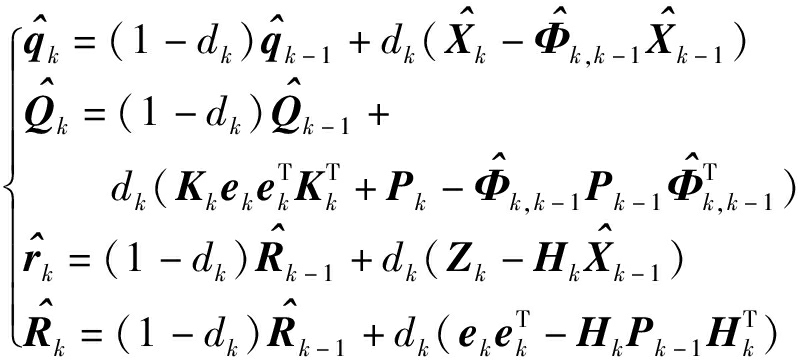
(16)
其中,dk=(1-b)/(1-bk+1),b为遗忘因子,取值为[0.95,0.99]。
自适应滤波算法是一种理论上具有高度灵活性的算法,旨在处理噪声不确定性较高的情况。该算法的一个显著特点是其理论上的能力,能够在不确定的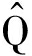k和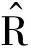k情况下同时计算这2个参数。然而,实际应用中,该方法在处理高度不确定性的系统时效果不佳。新息向量异常会影响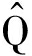k和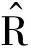k的计算,从而难以保证滤波结果的准确性。这意味着算法对异常值的敏感性可能导致估计结果的波动,进而影响决策的质量。此外,在滤波过程中,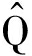k和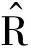k作为协方差矩阵,应保持正定,以确保估计过程的收敛性;若参数为非正定,那么滤波过程可能发散,导致估计结果不可靠。
为抑制滤波器的发散,在1.3节的基础上,引入异常检测机制,以识别滤波过程中的发散现象,据此在滤波过程中重新计算残差值。通过新息进行发散判断
(17)
式中 γ——实际误差与预期误差之间的比例界限
tr[·]——矩阵的求迹运算
若γ=1时,为最严格的收敛判据条件;若γ>1时,则说明实际误差是预期误差的γ倍,此时滤波已发散,需进行处理。
假设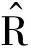k=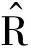k-1,可推导得
(18)
由式(17)、(18)可推出最严格收敛判断为
(19)
反之,滤波发散判断为
(20)
通过对模型预测误差协方差矩阵的加权更新,抑制滤波的发散。改正方法为
(21)
其中
(22)
综上,Pk/k-1求解式为
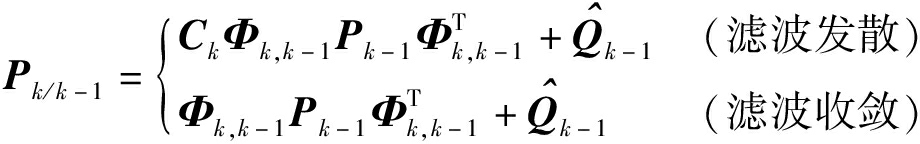
(23)
为了保证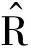k的正定性,加入时变量测噪声
dk=(1-b)/(1-bk+1)
(24)
(25)
在温室定位技术应用中,该算法的异常检测机制能够在定位过程中识别并调整异常数据,有效抑制了UWB定位中常见的多径效应和非视距对定位精度的影响。此外,算法通过计算加权系数对状态估计的均方误差矩阵进行动态校正,使滤波过程能够适应温室环境中的复杂信号波动,显著提升了定位精度和系统的稳定性。该方法增强了系统的鲁棒性,使定位系统能够快速响应并调整异常信号,减少滤波器发散的风险,从而保障UWB定位系统在温室环境中的长期稳定性和可靠性。
首先通过仿真对本文提出的定位算法进行分析。假设农用车辆匀速行驶,速度为0.012 m/s,逆时针方向从基站A出发依次经过基站A、B、C、D、A,形成正方形轨迹,顶点坐标依次为基站A(1 m,1 m)、基站B(5 m,1 m)、基站C(5 m,5 m)以及基站D(1 m,5 m)。初始协方差矩阵为P0=I4,过程噪声协方差矩阵为Q=0.01eye(4),其中eye()为单位矩阵。
为模拟小车在实际环境中受到不同程度量测噪声的影响,本文引入3个正均值高斯分布噪声R1、R2、R3,即R1=0.1+0.1randn(1),R2=0.5+0.5randn(1)和R3=1+randn(1)。在相同仿真环境中,分别使用UWB、KF、AKF以及IAKF算法进行处理。
理想情况下,目标轨迹呈现为一个5 m×5 m的正方形路径。图2展示了不同算法下轨迹效果对比,可以发现各算法对噪声的抑制效果存在差异。当噪声为R1时,各算法的轨迹与理想路径较为接近。随着噪声增大至R2和R3,未经过滤波处理的UWB轨迹逐渐偏离真实路径。而经过KF、AKF以及IAKF算法处理后的轨迹能够较好地跟踪真实路径。尤其是IAKF算法,在不同噪声水平下,其轨迹最接近真实路径,表现出优异的鲁棒性和抗噪能力。
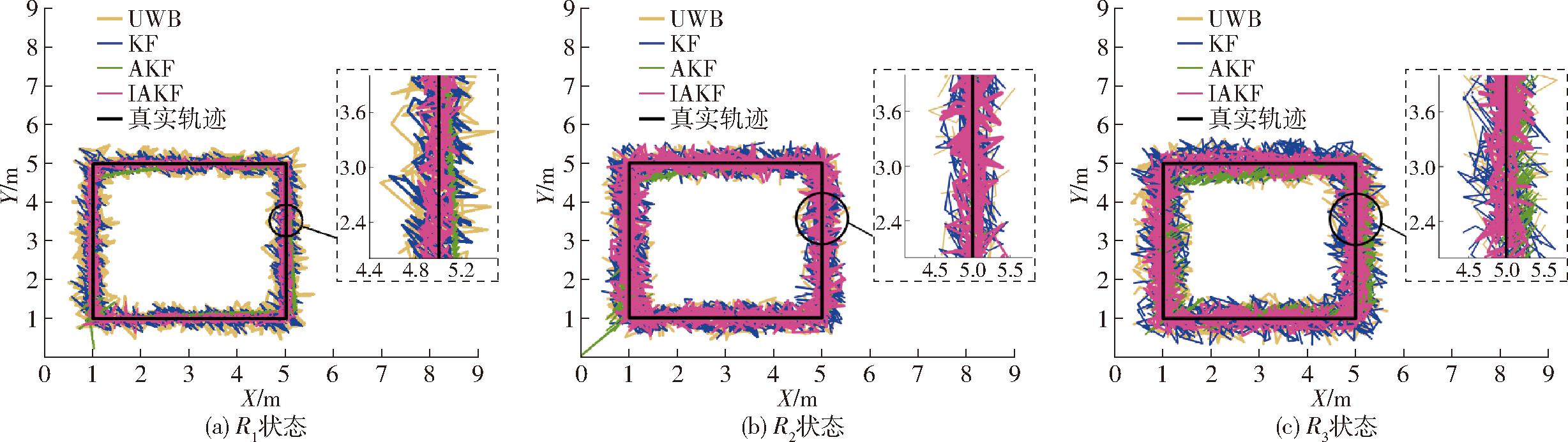
图2 模拟轨迹比较
Fig.2 Comparison of simulation trajectories
图3和图4展示了在UWB定位系统下,不同滤波算法在X轴和Y轴方向上的位置误差核密度分析图。图中颜色由红到蓝逐渐递减,表示误差密度从高到低的分布情况。随着噪声水平增加,KF算法在UWB系统中X轴和Y轴方向的误差密度集中区域逐渐偏离坐标轴,表明该算法定位精度迅速下降。AKF算法在X轴方向上表现出较好的误差控制能力,但Y轴方向的误差密度随噪声增大而扩大。IAKF算法在3种不同的噪声条件下,X轴和Y轴方向的密度集中区域保持在接近坐标轴的位置,凸显了抗噪性能和定位精度。
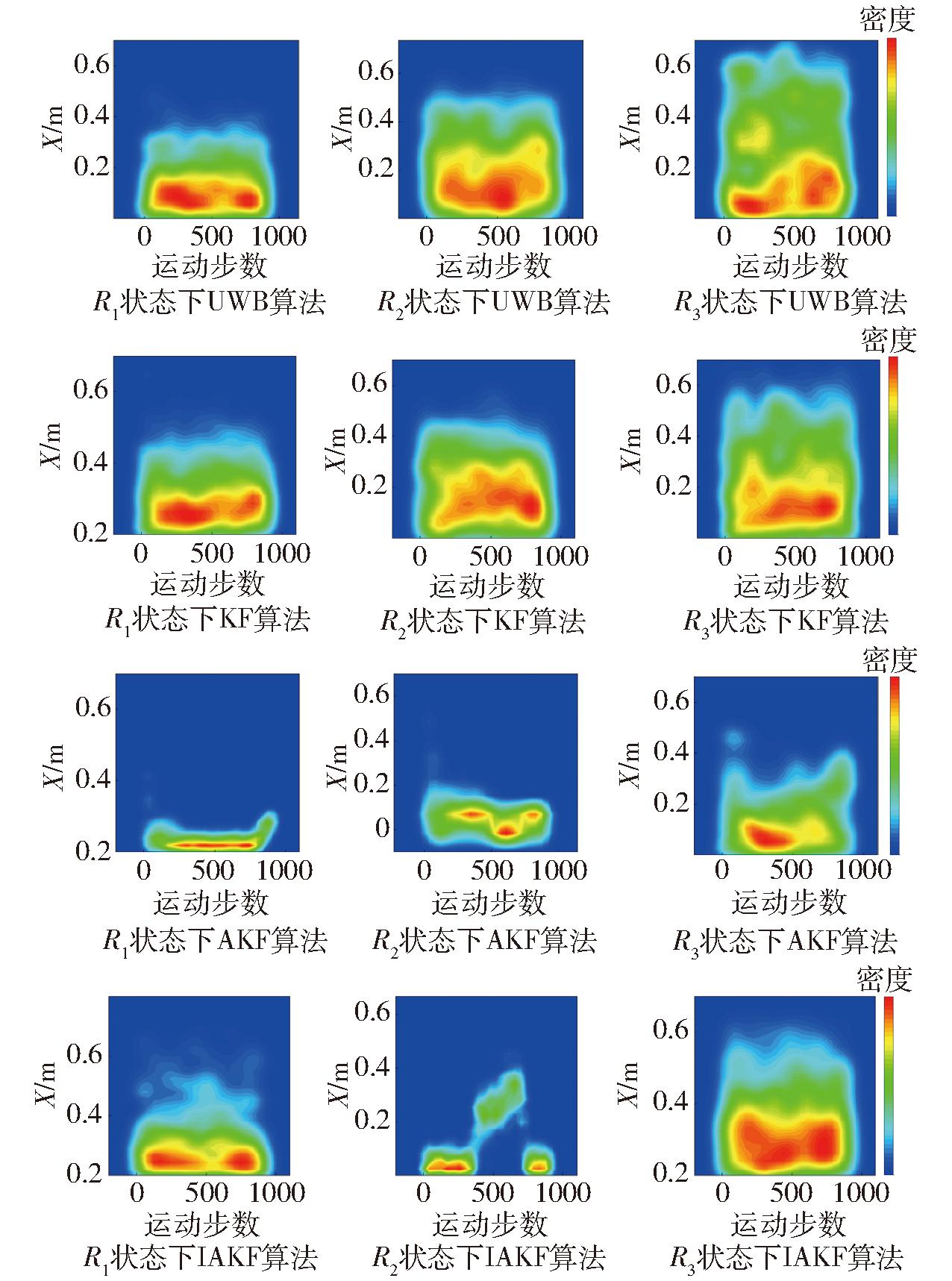
图3 X轴方向的算法误差密度
Fig.3 Algorithm error in X-axis direction
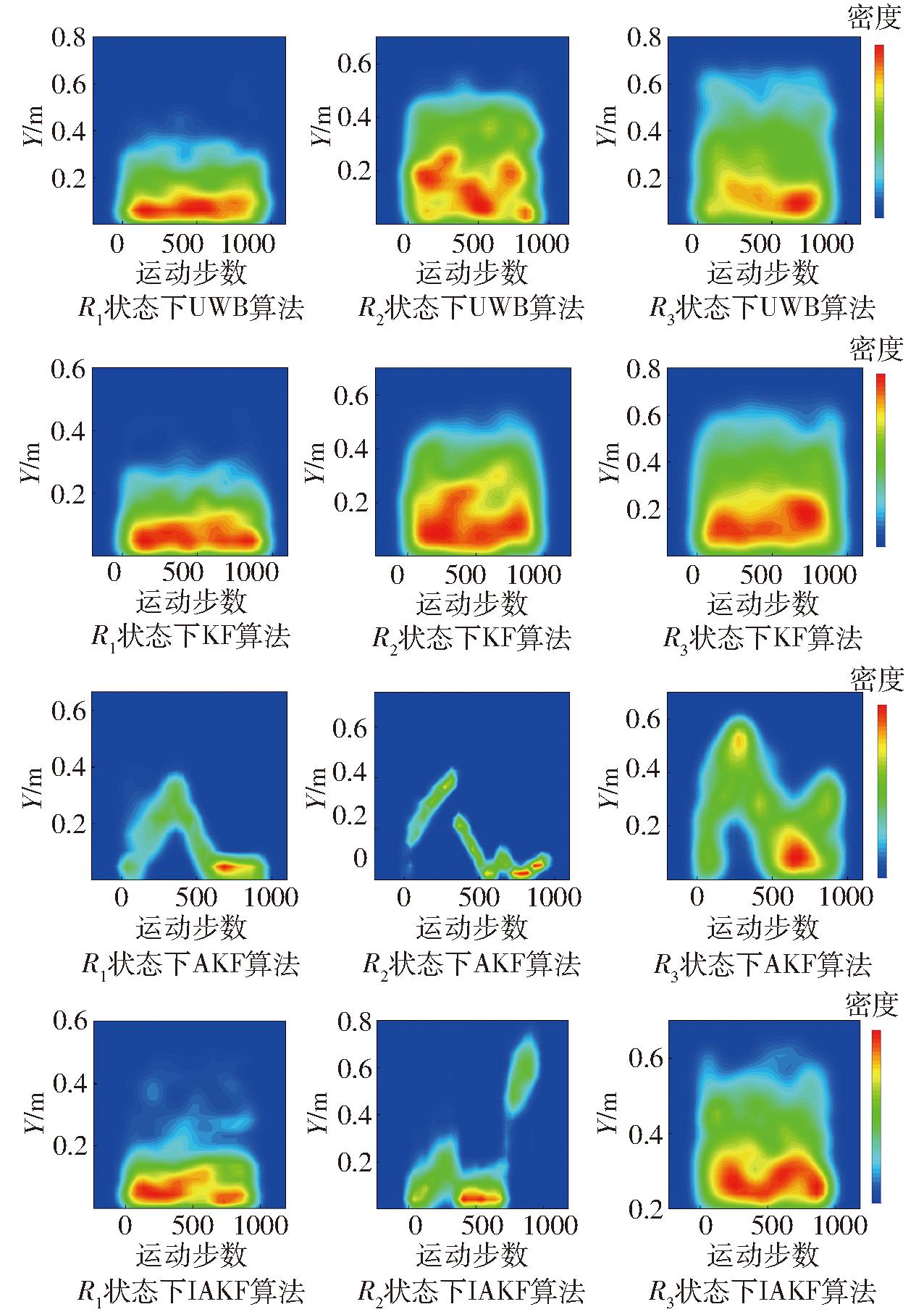
图4 Y轴方向的算法误差密度
Fig.4 Algorithm error in Y-axis direction
采用位置平均绝对误差(Mean absolute error,MAE)评估算法定位精度。
在模拟环境下,UWB、KF、AKF和IAKF算法误差均与噪声呈正比。其中,UWB和KF算法最大误差控制在0.7 m以内,AKF算法最大误差小于 0.6 m,而本研究提出的IAKF算法将最大误差控制在 0.5 m 以内。MAE如表1所示。
表1 模拟场景下位置误差
Tab.1 Position error in simulated scenarios m
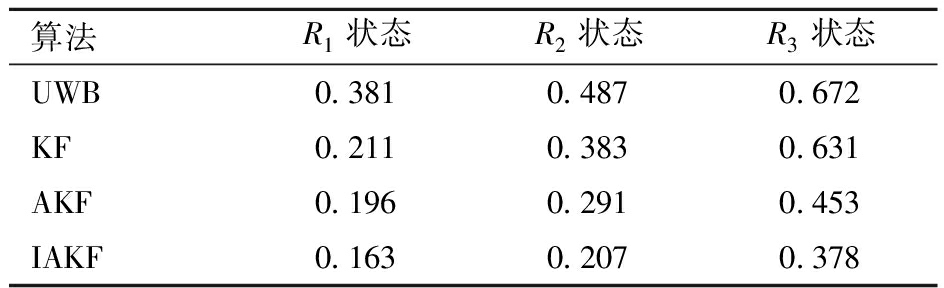
算法R1状态R2状态R3状态UWB0.3810.4870.672KF0.2110.3830.631AKF0.1960.2910.453IAKF0.1630.2070.378
为进一步验证本文提出算法的可行性,选用5个UWB模块进行农用履带车辆定位试验,UWB参数如表2所示,模块布置如图5所示。其中,4个模块配置为固定基站,分别为基站A、基站B、基站C及基站D,基站A与上位机相连;1个模块作为移动标签O,安装于农用履带车辆上,如图6所示。
表2 UWB参数
Tab.2 UWB parameters
参数数值/型号信号收发器DW1000芯片遵循标准IEEE802.15.4—2011频段/GHz3.5～6.5(6个RF频段)数据传输速率/(kb·s-1)110、850、6800
图5 UWB设备
Fig.5 UWB equipment
图6 农用履带车辆
Fig.6 Agricultural tracked vehicles
测试环境为温室,其顶部覆盖塑料薄膜,温室内存在铁丝网等障碍物,容易引起信号的反射和散射,从而导致多路径效应干扰。在这种情况下,信号经过不同路径到达接收端,产生时延和幅度衰减,使得UWB系统接收信号稳定性差。
试验区域为6 m×6 m的正方形空间,基站A、基站B、基站C、基站D分别置于该正方形定位区的4个顶点。在定位测试之前,为了减少基站间距偏差对定位精度的影响,需要对UWB系统进行校准。将基站A连接到上位机,设定为坐标原点(0,0),由此确定基站B的坐标为(6 m,0 m),并根据基站A和B的位置确定基站C和D的位置分别为(6 m,6 m)和(0 m,6 m)。根据系统的解算结果,微调基站B、C和D的位置。这一校准过程,旨在调整基站位置,确保每个基站的相对坐标准确,从而提升整个系统的定位精度。
在试验中,当履带车辆处于静止状态时,其位置固定在坐标(1 m,5 m)处;当车辆处于运动状态时,其运动路径规划通过Ubuntu系统下的机器人操作系统 (Robot operating system,ROS)工作空间编程实现。试验场景分为LOS和NLOS,其中LOS场景下定位区域保持空旷,不放置任何障碍物;NLOS场景下放置2个桩桶并有2名试验人员在定位区域中移动,分别如图7和图8所示。车辆实际运动轨迹为4 m×4 m的正方形,其路径区域的4个顶点的坐标分别为A′(1 m,1 m)、B′(5 m,1 m)、C′(5 m,5 m)和D′ (1 m,5 m),顺序为A′→B′→C′→D′→A′。
图7 LOS试验场地
Fig.7 LOS experimental site
图8 NLOS试验场地
Fig.8 NLOS experimental site
履带车辆处于静止状态下,UWB、KF、AKF、IAKF算法试验数据点如图9所示。从图9可以看出,UWB数据点分布较为分散,表明其定位精度相对较低;KF和AKF数据点比UWB更集中,但仍然有较大的分散性。IAKF数据点相对最为集中,接近真实位置,表明该算法在静止状态下定位精度更高。
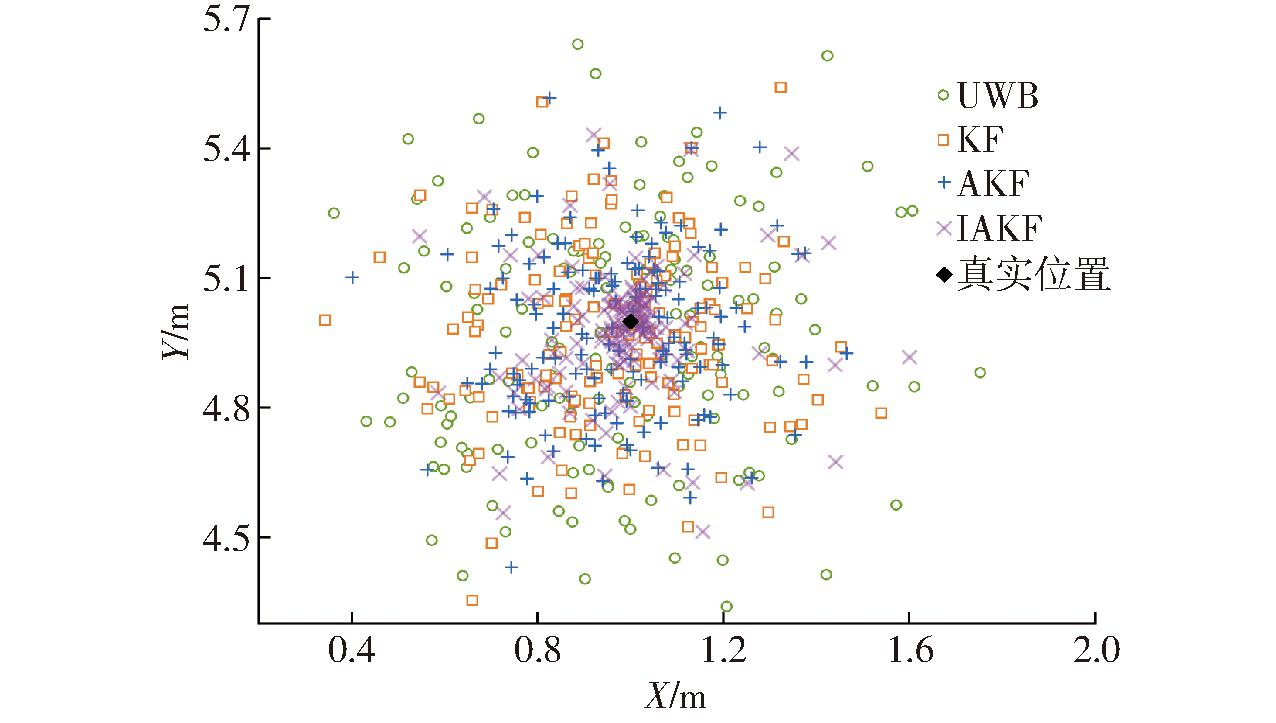
图9 静止状态下的数据点
Fig.9 Data points in stationary state
不同算法位置误差如图10所示。UWB算法波动幅度显著,且误差较大,MAE和最大误差分别为0.301 m和1.011 m。相比之下,KF和AKF算法误差波动有所减小,MAE分别为0.209 m和0.162 m,最大误差分别为0.732 m和0.652 m。IAKF算法的定位误差波动幅度最小,MAE仅为0.103 m,最大误差为0.597 m。KF、AKF、IAKF算法的MAE较UWB测量值分别提高30.6%、46.2%和65.8%。这表明,在温室试验环境中,IAKF算法能够有效抑制履带车辆处于静止状态下的定位发散问题。
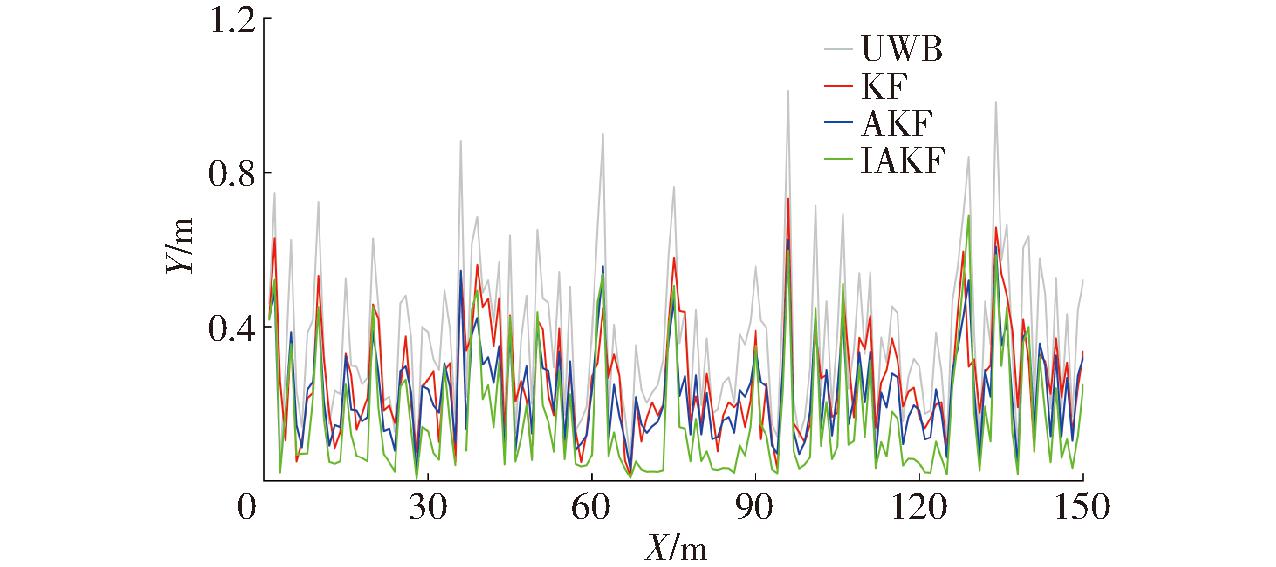
图10 静止状态下的位置误差比较
Fig.10 Comparison of position error in static state
履带车辆处于在LOS试验场景下,UWB、KF、AKF、IAKF算法试验轨迹如图11所示。UWB算法轨迹与真实轨迹偏差较大;KF和AKF算法运动轨迹有所改进。相比之下,IAKF算法轨迹与真实轨迹最为接近。
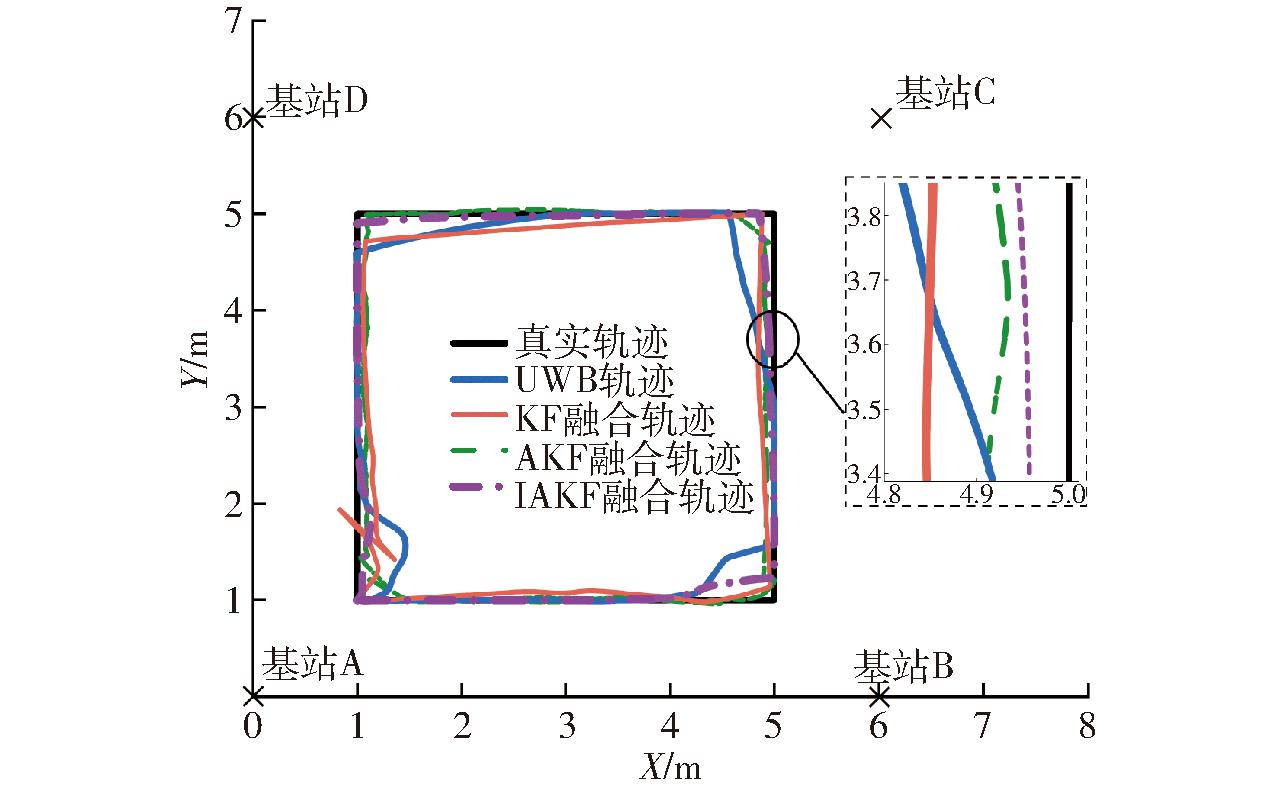
图11 LOS场景下试验轨迹
Fig.11 Test trajectory in LOS scenario
图12展示了KF、AKF、IAKF算法的位置误差对比情况,具体数据如表3所示。分析可得,3种算法的MAE值均能维持在0.3 m以内。精度较UWB原始观测值均有所提升,KF、AKF、IAKF算法MAE较UWB测量值分别提高29.6%、37.1%和45.3%。
表3 LOS场景下的位置误差
Tab.3 Position error in LOS scenario m
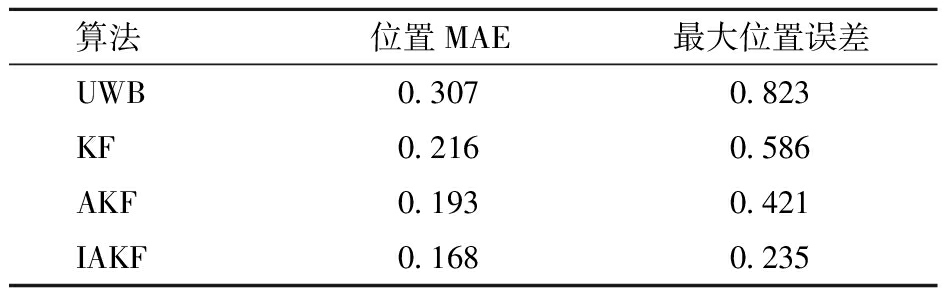
算法位置MAE最大位置误差UWB0.3070.823KF0.2160.586AKF0.1930.421IAKF0.1680.235
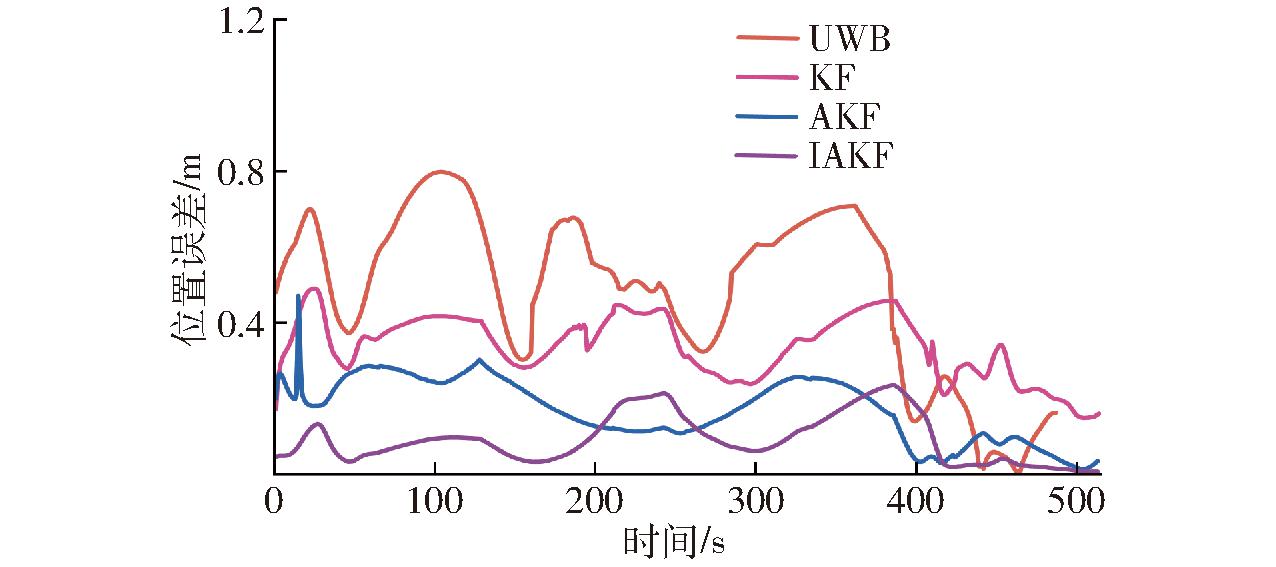
图12 LOS场景下位置误差比较
Fig.12 Comparison of position errors in LOS scenarios
由于受到铁丝网等障碍物干扰,UWB定位系统最大误差高达0.823 m。KF算法最大误差控制在0.6 m以下,AKF算法将误差控制在0.5 m以下,IAKF算法显著降低了误差,最大误差控制在0.3 m以内。这一结果表明,在LOS试验场景下,IAKF算法能有效地抑制履带车辆在运动状态下的定位测距误差和异常值。
图13展示了LOS试验场景下3种算法累积分布函数(Cumulative distribution function,CDF)图。由图13可知,IAKF算法CDF值较早趋近1,具有更快的收敛速度。
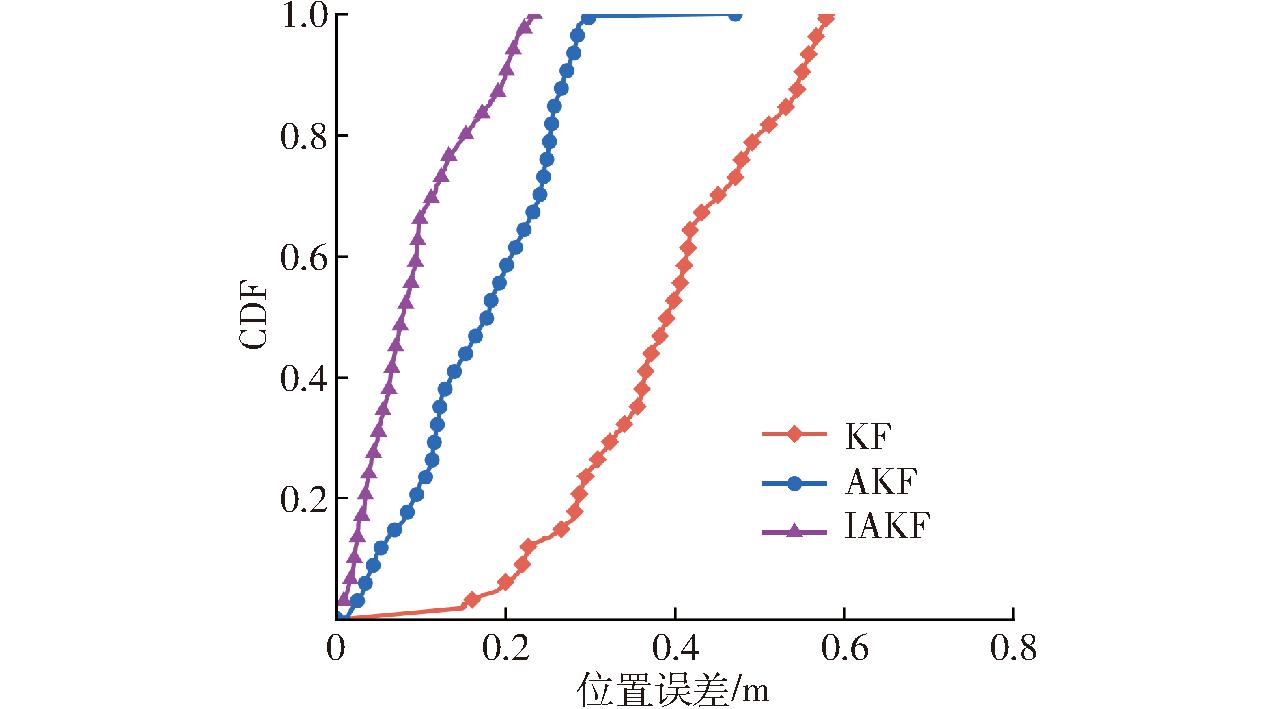
图13 LOS场景下CDF比较
Fig.13 Comparison of CDF in LOS scenario
履带车辆处于在NLOS试验场景下,试验区域内摆放2个桩桶,并安排2位试验人员在区域内随机走动,以模拟NLOS场景下UWB定位所受到的不确定性干扰。
NLOS场景下各滤波算法试验轨迹如图14所示。UWB算法与真实轨迹偏差较大,体现出其在NLOS环境中的定位精度较低;KF和AKF算法相比UWB有所改善,但仍存在一定偏差。IAKF算法则在NLOS条件下展现出最接近真实轨迹的效果。
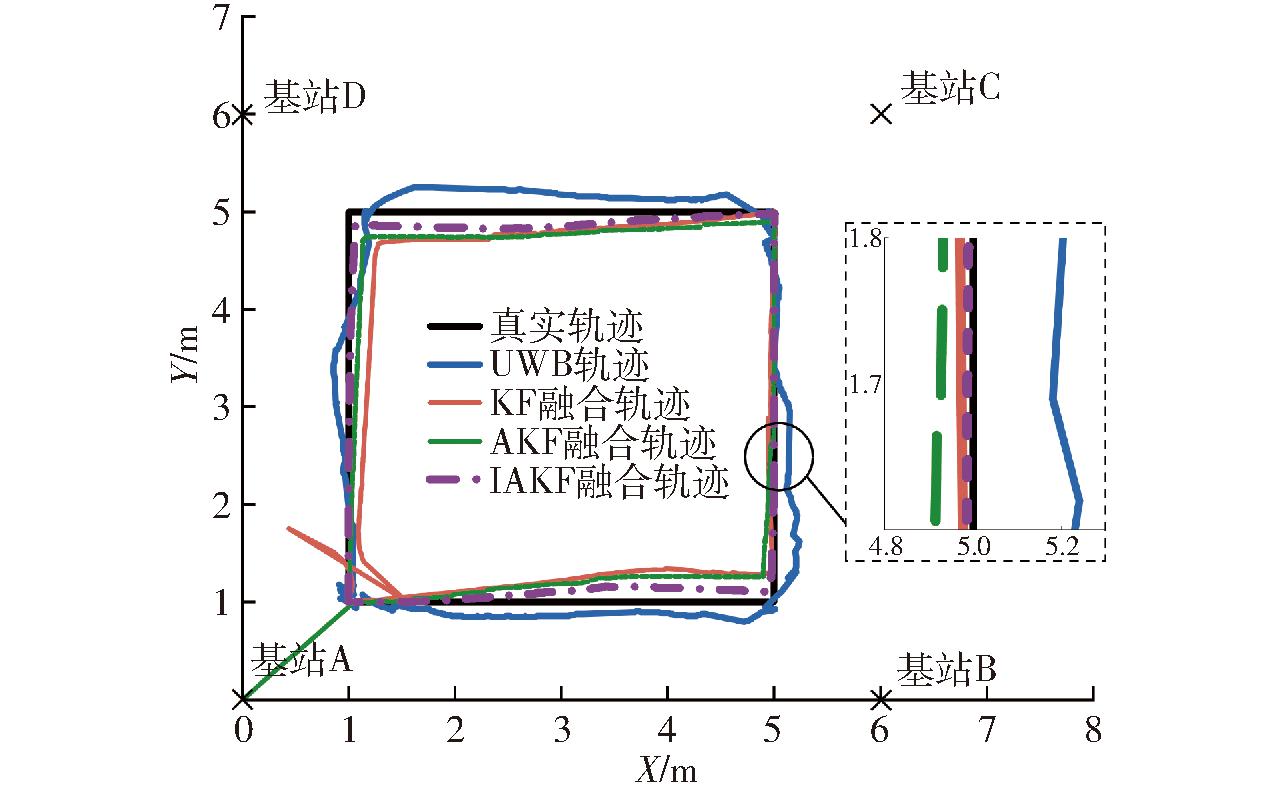
图14 NLOS场景下试验轨迹
Fig.14 Test trajectory in NLOS scenario
KF、AKF、IAKF算法位置误差如表4所示。分析可得,3种算法MAE均能维持在0.4 m以内。精度较UWB原始观测值均有所提升,KF、AKF、IAKF算法MAE较UWB测量值分别提高22.9%、27.2%和38.3%。这一结果表明,在NLOS试验场景下,IAKF算法能有效地抑制履带车辆在运动状态下定位测距误差和异常值。
表4 NLOS场景下位置误差
Tab.4 Position error in NLOS scenario m
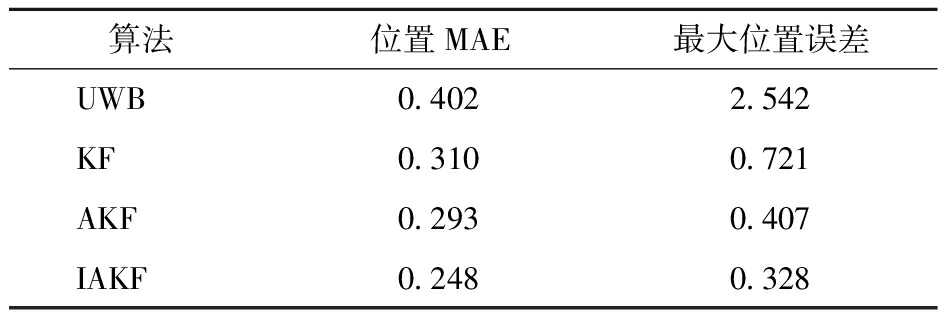
算法位置MAE最大位置误差UWB0.4022.542KF0.3100.721AKF0.2930.407IAKF0.2480.328
图15展示了NLOS试验场景下3种算法CDF。由图15可知,IAKF算法CDF曲线在较小的定位误差范围内较早趋近1,表明IAKF算法在NLOS场景下具备更高的定位精度。
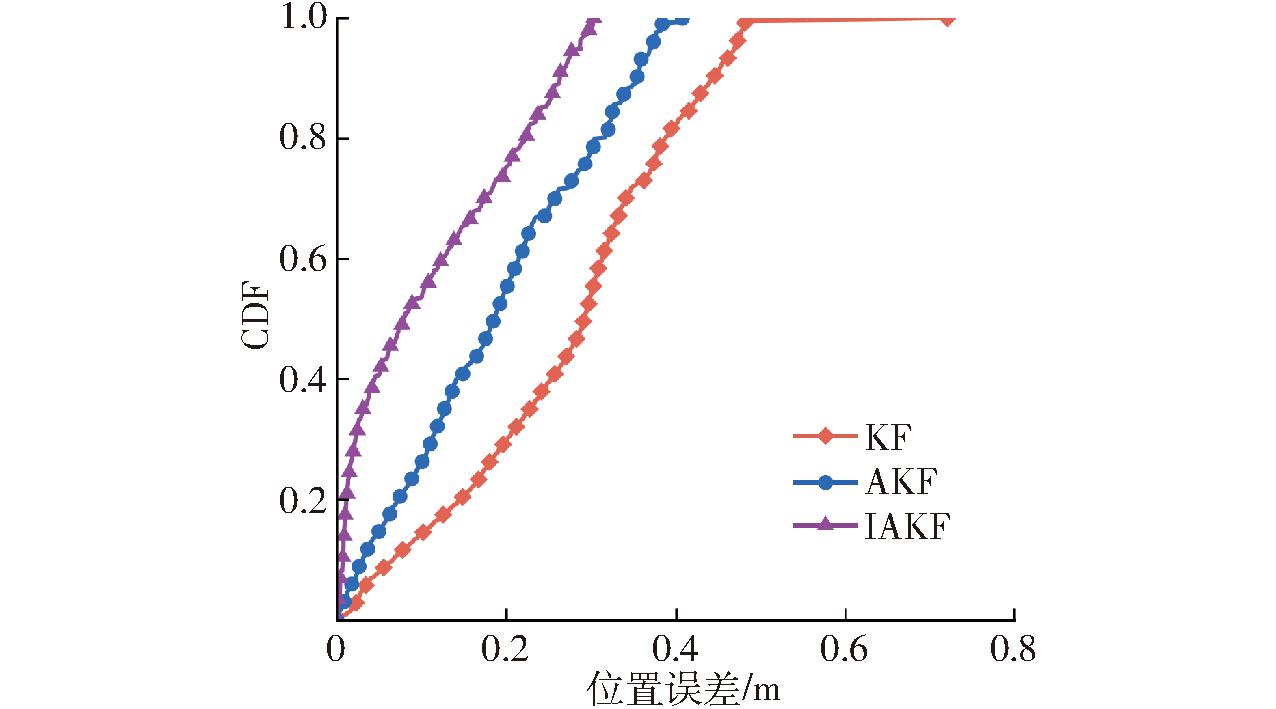
图15 NLOS场景下CDF比较
Fig.15 Comparison of CDF in NLOS scenario
(1)提出基于IAKF的UWB温室定位技术。通过自适应滤波技术降低了量测噪声对定位精度的负面影响,有效处理了目标车辆在温室环境下的运动轨迹。
(2)仿真试验结果表明,UWB、KF算法最大误差达到0.7 m左右,AKF算法最大误差小于0.6 m,而IAKF算法最大误差控制在0.5 m以下。
(3)温室实车试验结果表明,IAKF算法在静止和运动状态下MAE分别稳定在0.2 m和0.4 m。当履带车辆处于静止状态时,IAKF的MAE比 KF和AKF算法分别提高50.7%和36.4%;在车辆处于运动状态时,IAKF算法在LOS和NLOS场景中的定位精度较KF和AKF算法分别提升22.2%、13.0%和20.0%、15.4%。由于IAKF算法无需复杂的硬件支持和高计算资源,使其在实际农业应用中具有较高的经济性和可行性。
[1] SUN R,WANG J,CHENG Q,et al.A new IMU-aided multiple GNSS fault detection and exclusion algorithm for integrated navigation in urban environments[J].GPS Solutions,2021,25(4):1-17.
[2] CHENG Q,CHEN W,SUN R,et al.RANSAC-based instantaneous real-time kinematic positioning with GNSS triple-frequency signals in urban areas[J].Journal of Geodesy,2024,98(4):1-19.
[3] VICENZO S,XU B,XU H,et al.GNSS direct position estimation-inspired positioning with pseudorange correlogram for urban navigation[J].GPS Solutions,2024,28(2):83.
[4] 刘禹汐,杨浩然,韩冰,等.基于多传感器融合的拖拉机侧滑量估计方法及其验证[J].农业机械学报,2023,54(增刊2):400-408,426.LIU Yuxi,YANG Haoran,HAN Bing,et al.Side-slip estimation method based on multi-sensor fusion and its validation[J].Transactions of the Chinese Society for Agricultural Machinery,2023,54(Supp.2):400-408,426.(in Chinese)
[5] YI D,ZHETAO Z,LILI P,et al.Partial ambiguity resolution considering the multipath effects in a canyon environment[J].Survey Review,2024,56(396):300-315.
[6] 邹璇,付睿男,王亚伟,等.测站处GNSS多路径误差效应反演及其应用研究[J].武汉大学学报(信息科学版),2022,47(9):1416-1421.ZOU Xuan,FU Ruinan,WANG Yawei,et al.Inversion of GNSS multipath effects around the stations and its applications[J].Geomatics and Information Science of Wuhan University,2022,47(9):1416-1421.(in Chinese)
[7] WANG Y,FU S,WANG F.Improved maximum correntropy criterion Kalman filter with adaptive behaviors for INS/UWB fusion positioning algorithm[J].Alexandria Engineering Journal,2024,109:702-714.
[8] 刘韬,徐爱功,隋心,等.新息向量的抗差Kalman滤波方法及其在UWB室内导航中的应用[J].武汉大学学报(信息科学版),2019,44(2):233-239.LIU Tao,XU Aigong,SUI Xin,et al.An improved robust Kalman filtering method based on innovation and its application in UWB indoor navigation[J].Geomatics and Information Science of Wuhan University,2019,44(2):233-239.(in Chinese)
[9] CRISTODARO C,RUOTSALAINEN L,DOVIS F.Benefits and limitations of the record and replay approach for GNSS receiver performance assessment in harsh scenarios[J].Sensors,2018,18(7):2189.
[10] CHE F,AHMED Q Z,LAZARIDIS P I,et al.Indoor positioning system (IPS) using ultra-wide bandwidth (UWB) for industrial internet of things (IIOT)[J].Sensors,2023,23(12):5710.
[11] HANZEL K,GRZECHCA D.Increasing the security of smart cities of the future thanks to UWB technology[C]∥European,Mediterranean,and Middle Eastern Conference on Information Systems.Cham:Springer International Publishing,2021:585-596.
[12] CHAKRABORTY M,KANDAR D,MAJI B.Integrated radar radio:enabling technology for smart vehicle of smart cities[J].International Journal of Autonomous and Adaptive Communications Systems,2023,16(4):391-403.
[13] WANG Z,SPASOJEVIC P,SCHLAKE B W,et al.Development and testing of a UWB-based vehicle-to-vehicle (V2V) ranging system for self-propelled rail vehicles[J].IEEE Transactions on Vehicular Technology,2023,73(3):3247-3261.
[14] ZHU B,TAO X,ZHAO J,et al.An integrated GNSS/UWB/DR/VMM positioning strategy for intelligent vehicles[J].IEEE Transactions on Vehicular Technology,2020,69(10):10842-10853.
[15] 解开婷,张兆国,王法安,等.基于全质心WLS-HDS-TWR算法的无人驾驶农业机械协同定位算法研究[J].农业机械学报,2024,55(7):27-36,110.XIE Kaiting,ZHANG Zhaoguo,WANG Faan,et al.Cooperative localization algorithm for full center mass of WLS-HDS-TWR driverless agricultural machines[J]Transactions of the Chinese Society for Agricultural Machinery,2024,55(7):27-36,110.(in Chinese)
[16] 王法安,殷国栋,庄伟超,等.基于多基站IMMKF-DOA辅助车辆协同定位算法研究[J].机械工程学报,2023,59(4):125-134.WANG Faan,YIN Guodong,ZHUANG Weichao,et al.IMMKF-DOA auxiliary vehicle cooperative localization algorithm based on multi-base station[J].Journal of Mechanical Engineering,2023,59(4):125-134.(in Chinese)
[17] 毕松,张国轩,李志军,等.基于测距值修正的温室植保机器人定位方法[J].农业机械学报,2023,54(8):347-358.BI Song,ZHANG Guoxuan,LI Zhijun,et,al.Positioning method of greenhouse plant protection robot based on distance measurement value correction[J].Transactions of the Chinese Society for Agricultural Machinery,2023,54(8):347-358.(in Chinese)
[18] 刘艳伟,李思雯,杨启良,等.基于UWB定位的智能温室三维温湿度检测系统研究[J].农业机械学报,2023,54(9):414-422.LIU Yanwei,LI Siwen,YANG Qiliang,et,al.Design of intelligent greenhouse three-dimensional temperature and humidity detection system based on UWB positioning[J].Transactions of the Chinese Society for Agricultural Machinery,2023,54(9):414-422.(in Chinese)
[19] 林相泽,王祥,林彩鑫,等.基于超宽带的温室农用车辆定位信息采集与优化[J].农业机械学报,2018,49(10):23-29,45.LIN Xiangze,WANG Xiang,LIN Caixin,et,al.Location information collection and optimization for agricultural vehicle based on UWB[J].Transactions of the Chinese Society for Agricultural Machinery,2018,49(10):23-29,45.(in Chinese)
[20] SCHMIDT S O,CIMDINS M,JOHN F,et al.SALOS-a UWB single-anchor indoor localization system based on a statistical multipath propagation model[J].Sensors,2024,24(8):2428.
[21] WANG S,WANG H,WANG G,et al.Algorithm design to identify targets from multipath ghosts and clutters for SISO IR-UWB radar:incorporating waveform features and trajectory[J].IEEE Sensors Journal,2023,24(2):2278-2288.
[22] LI Y,XU L,WANG P,et al.Ultra-wideband radar detection based on target response and time reversal[J].IEEE Sensors Journal,2024,24(9):14750-14762.
[23] HE X,MO L,WANG Q.An Attention-Assisted UWB ranging error compensation algorithm[J].IEEE Wireless Communications Letters,2022,12(3):421-425.
[24] ZHANG H,ZHOU X,ZHONG H,et al.A dynamic window-based UWB-Odometer fusion approach for indoor positioning[J].IEEE Sensors Journal,2022,23(3):2922-2931.
[25] ZABALEGUI P,DE MIGUEL G,GOYA J,et al.Residual based fault detection and exclusion methods applied to ULTRA-WIDEBAND navigation[J].Measurement,2021,179:109350.
[26] CHENG L,CHEN Y,GUAN J.INS/UWB multi-sensor integrated localization scheme in indoor LOS/NLOS environment based on MEF-GPDAF[J].Computers and Electrical Engineering,2024,120:109693.
[27] WANG Y,ZHOU Y,LU Y,et al.MSTSCKF-based INS/UWB integration for indoor localization[J].Ain Shams Engineering Journal,2024,15(10):102939.
[28] PAN Hao,QI Xiaogang,LIU Meili,et al.Indoor scenario-based UWB anchor placement optimization method for indoor localization[J].Expert Systems with Applications,2022,205:117723.
[29] LIU Qingzhi,YIN Zhendong,ZHAO Yanlong,et al.UWB LOS/NLOS identification in multiple indoor environments using deep learning methods[J].Physical Communication,2022,52:101695.
[30] CHEN Y Y,HUANG S P,WU T W,et al.UWB system for indoor positioning and tracking with arbitrary target orientation,optimal anchor location,and adaptive NLOS mitigation[J].IEEE Transactions on Vehicular Technology,2020,69(9):9304-9314.
[31] 胡晓强,武东杰,彭侠夫.INS/GNSS/VO组合导航系统复合型异常检测与容错算法[J].中国惯性技术学报,2023,31(2):148-156.HU Xiaoqiang,WU Dongjie,PENG Xiafu.Compound anomaly detection and fault tolerance algorithm for INS/GNSS/VO integrated navigation system[J].Journal of Chinese Inertial Technology,2023,31(2):148-156.(in Chinese)
[32] STAHLKE M,KRAM S,OTT F,et al.Estimating TOA reliability with variational autoencoders[J].IEEE Sensors Journal,2021,22(6):5133-5140.
[33] 杨波,刘枫,薛亮,等.一种有色噪声条件下的改进卡尔曼滤波算法[J].中国惯性技术学报,2023,31(10):1004-1009.YANG Bo,LIU Feng,XUE Liang,et al.An improved Kalman filter algorithm under colored noise[J].Journal of Chinese Inertial Technology,2023,31(10):1004-1009.