随着全球农业自动化快速发展,智能采摘机器人在现代果园中的应用日益受到重视。苹果作为全球广泛种植的水果之一,其采摘效率对于整个产业链效益至关重要。然而,传统的人工采摘方式已无法满足现代农业对高效、低成本生产的需求。因此,研发能够自主决策的智能采摘机器人成为推动苹果产业可持续发展的重要手段[1]。
智能采摘机器人通过路径规划算法高效完成多目标果实的采摘任务。在多目标采摘过程中,规划合理的采摘路径顺序是确保采摘过程连续性和优化作业效率的关键问题之一[2]。果园环境复杂多变,树木高度、果实分布以及障碍物都会对采摘路径产生影响[3]。近年来,针对果园环境下多目标连续采摘的机械臂路径规划问题,研究人员提出了多种优化方法。遗传算法和蚁群算法作为全局优化算法,尽管在路径规划中能够找到较优解,但由于计算复杂度高、耗时较长,在实时采摘任务中的应用受限[4-5]。A*算法和人工势场法也常用于路径规划,但在高维复杂空间中多自由度机械臂应用中表现不佳[6-9]。快速扩展随机树(RRT)算法因具有快速适应复杂约束环境的能力受到广泛关注,但其随机性会导致路径次优化问题[10-11]。LAVALLE等[12]提出了RRT*算法,RRT*算法相比于RRT算法改变了父节点选取方式,并且增加了剪枝优化过程来获得全局下的最优路径,该方法优化了路径规划长度,但路径规划速度仍未解决。因此,一些学者使用双向路径规划算法来解决该问题[13-14],此类算法同时从起始点和目标点构建两棵RRT树,并在树之间进行探索和连接,通过双向扩展减少了路径规划时间,WANG等[15]提出了四随机树并行,但这些方法仍在全局环境中进行采样,未能提升路径规划效率。为解决该问题,部分学者通过约束随机采样点采样范围来缩小采样空间,从而得到全局最优解[16-17]。其中GAMMELL等[18]提出Informed-RRT算法,该方法是对RRT算法的采样过程进行优化得到的算法,利用椭圆采样方式来代替全局均匀采样。为了提高采摘效率,熊俊涛等[19]提出了一种结合人工势场法的四向搜索RRTstar算法,通过人工势场法对空间进行分割,获取空间分割点xsplit,进行四向搜索,提高了路径规划效率。此外,CAO等[20]引入目标重力场改进RRT算法,通过加快路径搜索,提高了采摘机器人路径规划效率,特别是在荔枝采摘机器人中的应用表现良好。虽然改进算法具有较高的效率与较快的运行速度,但在复杂场景下表现仍有缺陷。
针对非结构化环境下多枝叶遮挡的苹果连续采摘问题,本文提出一种改进的路径规划算法。通过优化RRT*算法的采样方式、扩展方向和步长,引入目标引导机制,以提升路径规划效率。考虑到采摘过程中枝叶的空间干扰,算法提出树枝密集度参数Ddensity与粒子群优化算法相结合,确定最优采摘顺序,高效生成适用于机械臂多目标采摘的最优路径,缩短采摘路径总长度,减少采摘路径规划时间,以期为苹果采摘机器人在执行多目标采摘任务时提供参考和技术支持。
当前苹果园培植方式主要采用现代化密植栽培技术,以提高产量和管理效率。苹果树树高一般控制在2.5~3.5 m之间,便于机械化采摘和修剪。株距通常在1.0~1.5 m,行距则在3~4 m之间,移动采摘机器人在树行之间作业,依靠机械臂执行采摘任务。果树结构复杂,由树干、树枝、果实和枝叶组成,其中树干和粗壮的树枝是需要重点避让的障碍物,未成熟的果实也需要识别避开。通过Blender软件建模,先创建一个圆柱体作为主干,后创建不同形状的树枝,移动并放在主干合适位置,使用球体创建苹果模型沿树枝分布,将苹果放置合适位置,用平滑雕刻工具细化模型最终可创建苹果树模型,把文件另存为STL格式并导入Matlab,得到仿真模型如图1所示。
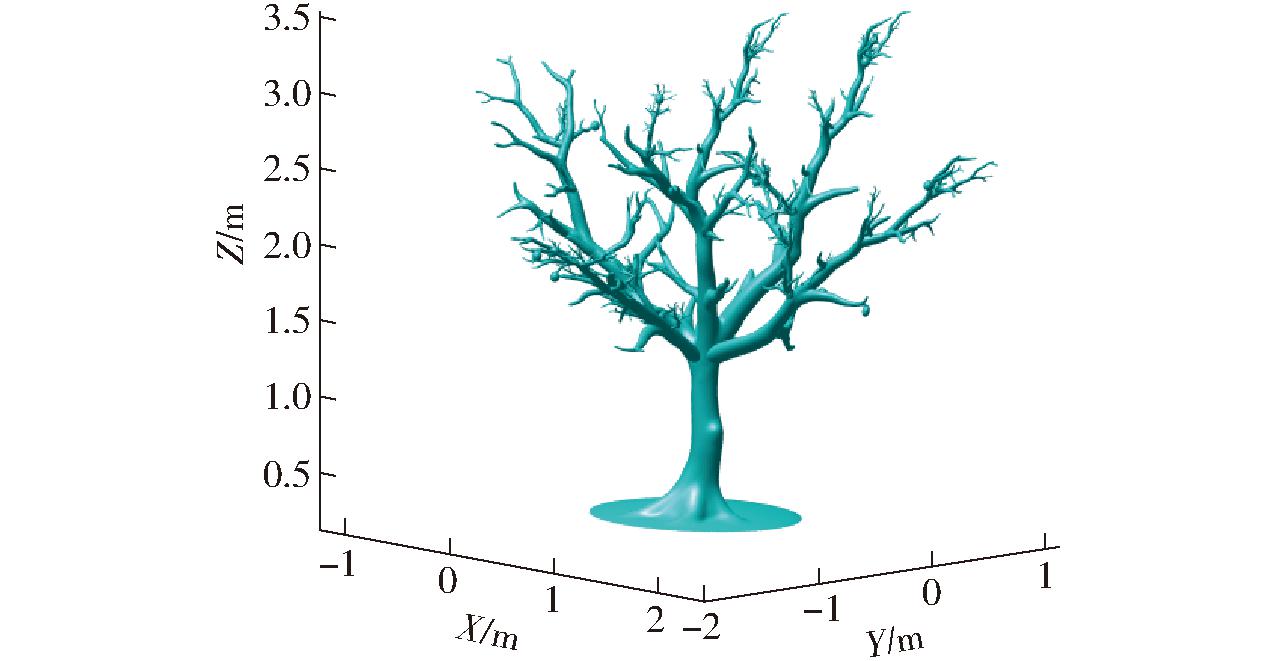
图1 苹果树模型
Fig.1 Apple tree model diagram
采摘时应确保机械臂在规划路径时能避开树干、粗枝和果实,从而在复杂环境中安全高效移动,避免损坏果树或果实。通过分析树冠和果实分布,还可以进一步优化采摘路径,减少机械臂移动时间和能耗,提升整体采摘效率。
为提高路径生成效率,提出了TG-RRT*算法,通过对RRT*引入自适应步长策略、目标区域采样调整、路径优化等方法,增强了算法扩展导向性,进一步缩短了路径长度,减少了路径生成时间。
传统的RRT与RRT*算法在扩展时从最近节点向随机采样点延伸一段固定距离。然而,固定步长可能导致拓展效率不高:步长过大会导致路径不够精细,难以避开障碍物;步长过小则可能增加计算量,延缓收敛速度。因此,不同步长直接影响算法扩展效率和路径质量。因此,本文引入一种自适应步长调节策略,该策略主要包括初始步长设定以及在靠近枝干时对步长的动态调整[21]。初始步长为
λinitial=ω1M
(1)
其中
(2)
式中 λinitial——初始步长
M——任务空间尺寸
ω1——环境复杂系数
Vo——障碍物总体积
davg——障碍物之间平均距离
Ls——任务空间特征长度
No——环境中树枝数量
Dvar——枝干分布方差
α1、α2、α3、α4——权重
权重可以通过经验或优化方法来确定,以平衡各因素的重要性。通过式(1)利用环境信息确定初始步长,但在靠近枝干拓展节点时易与枝干产生碰撞。为此本文提出了一种针对近枝干动态步长调整方法,如图2所示,在节点扩展过程中,如遇到碰撞,将采取缩小步长策略并重新进行碰撞检测;若此时未检测到碰撞,则该节点将被纳入搜索树。
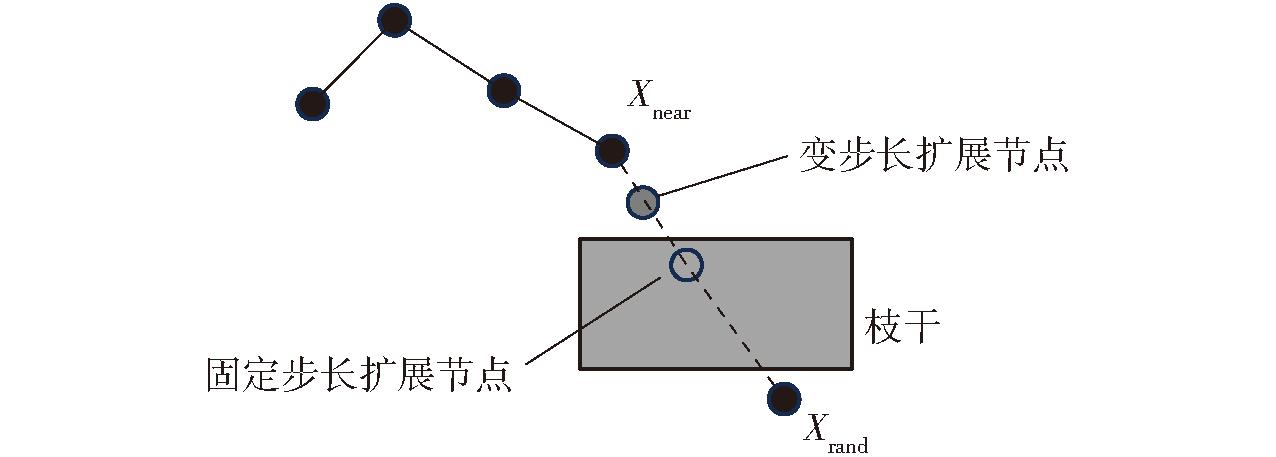
图2 动态步长调整示意图
Fig.2 Schematic of dynamic step length adjustment
步长λnow计算式为
λnow=ω2λinitial
(3)
式中 ω2——系数,取0.1~0.5
RRT*算法相较于RRT算法优化了路径,但扩展节点时,算法依赖于随机采样,这可能导致在某些区域节点分布稀疏,影响了路径连通性和优化效果。针对上述问题,TG-RRT*算法在目标区域内引入目标偏向策略进行采样,使随机采样点以更大的概率向目标点采样,并采用直连策略完成路径规划,便于更快地搜索到路径。
2.2.1 目标区域调整
传统RRT算法采样范围是整个搜索空间,其中采样点可以位于任意位置,导致采样效率低、收敛速度慢。为了减小采样范围使采样点更快地收敛到目标点附近,本算法设定目标区域进行采样。由于在果园采摘过程中,机械臂起始位置到采摘位置前很长一段距离无遮挡区域,所以可把采摘区域划分为无碰撞区域与枝叶碰撞区域。
考虑空间中路径规划时,从起始点到目标点规定目标区域内采样,改进后初始采样范围是以目标点向起始点方向延长线上距离起始点为两个步长的点作为顶点,与以起始点为圆心、以初始步长为半径的球体相切的等边圆锥。如图3所示,其中r为初始步长,h为起始点到目标点的距离,R为等边圆锥体底面半径。规定采样区域为等边圆锥是由于在实际采摘过程中,越靠近目标采摘果实枝叶遮挡越密集,往往在初始路径阶段是无碰撞区域,所以以一个收敛到扩散的等边圆锥区域进行采样,图4为目标区域划分与采样范围示意图。
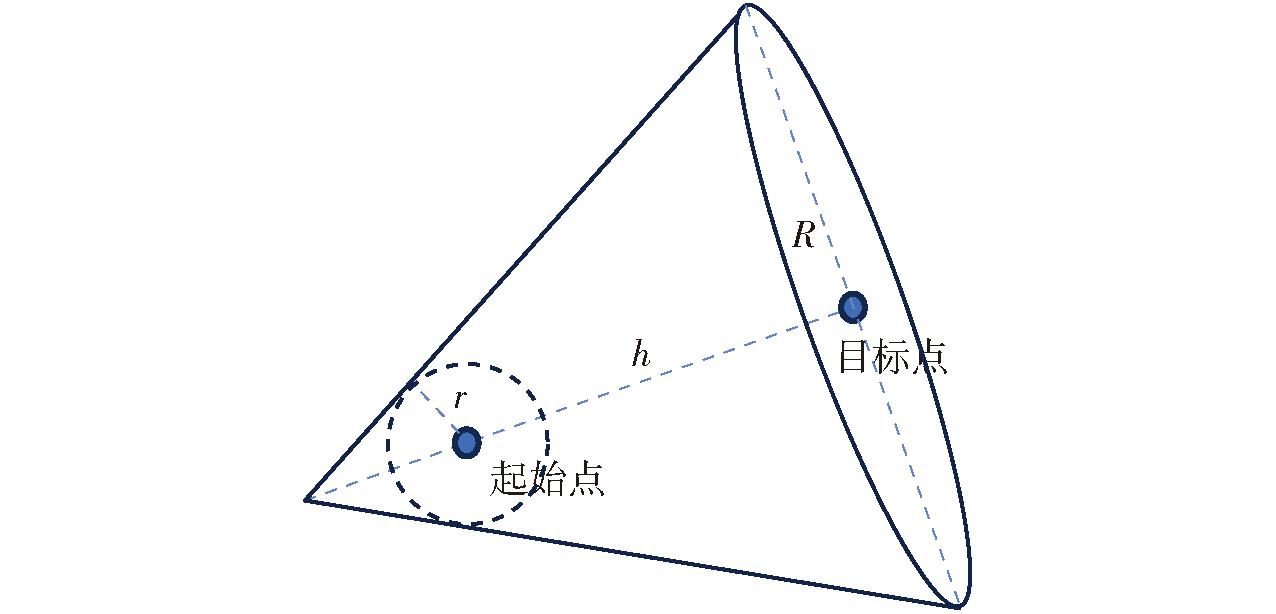
图3 目标区域原理图
Fig.3 Target area schematic
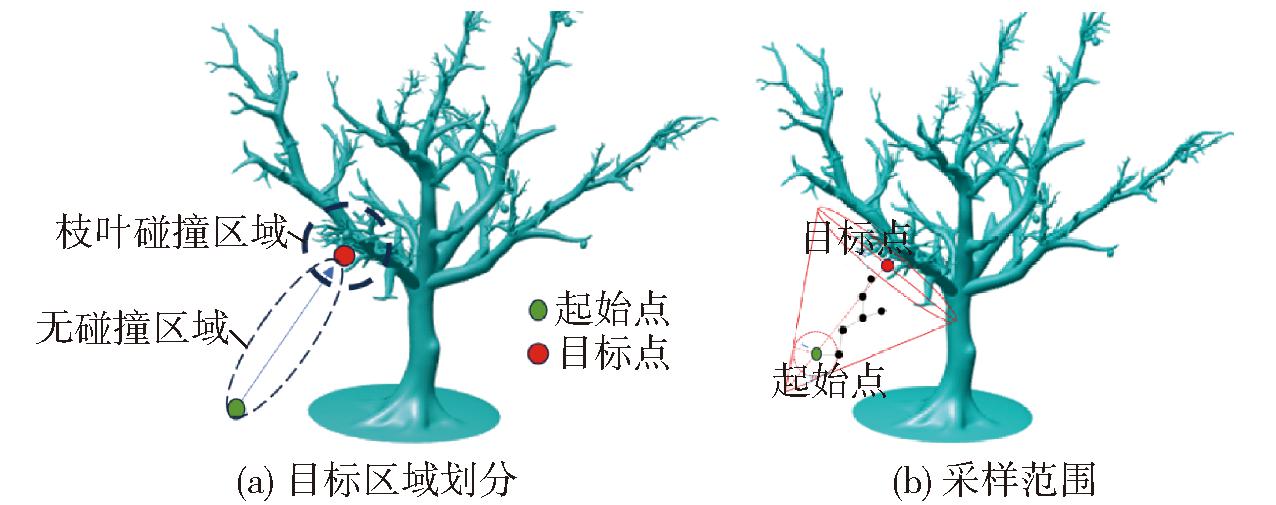
图4 目标区域划分与采样范围示意图
Fig.4 Schematics of target area division and sampling range
2.2.2 目标偏向策略
为了提升算法拓展效率,设定一个阈值,阈值为0~1。在生成随机状态点时,通过均匀随机数生成一个概率。通过比较设定阈值和概率来决定采样策略[22]。如果概率小于阈值,在规定的目标等边圆锥采样区域内随机采样点使用目标偏向采样,此时目标点作为参考方向。如果概率大于等于阈值,则在目标等边圆锥采样区域内根据当前随机状态点进行采样。目标偏向策略为
(4)
式中 Xrand——随机状态点 Xgoal——目标点
Prand——阈值 P——概率
Q——区域内采样点
2.2.3 直连策略
在RRT*算法扩展的新节点接近目标点时,即便它与目标点之间没有障碍物,由于随机采样的特性和固定步长的设置,可能无法顺利地连接到目标。这种情况会导致搜索过程效率降低,进而增加整体路径规划所需的时间。为了解决这一问题,算法引入直连策略,如图5所示。在随机树扩展过程中,当新节点到目标点距离不超过设定初始步长,且进行碰撞检测符合连接条件时,将采样点与目标点直接相连,并终止后续节点扩展。
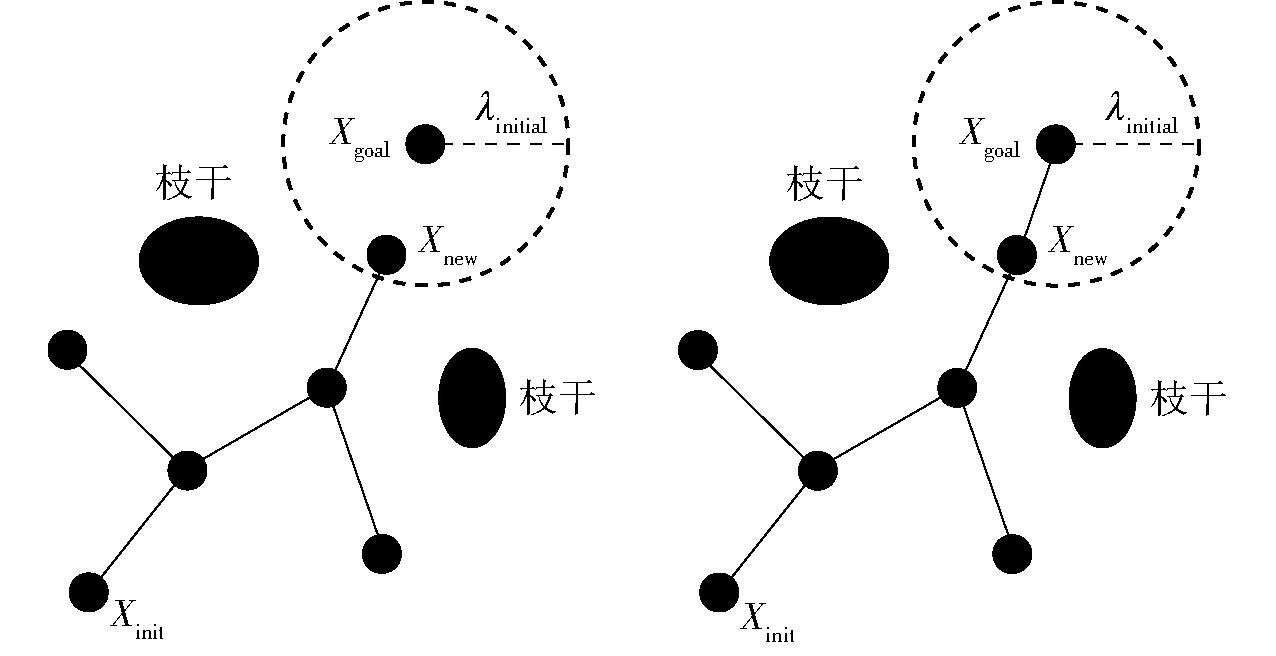
图5 直连策略示意图
Fig.5 Direct connection strategy diagram
以目标点Xgoal为圆心,以初始步长λinitial为半径确定直连策略使用范围,当扩展新节点Xnew到达此范围则直接将新节点与目标点连接,完成路径规划。
首先去除路径中的冗余点,冗余点清除的目的是获得较短的本地路径[23],如图6所示,其中黑色线条为算法初始规划路径,红色虚线为尝试连接路径,绿色线条为删除冗余点后路径。从起始点开始检测路径上连续节点之间的直线连通性,移除那些不影响路径连通性的中间节点,从而得到更短的路径。当枝叶较多时,由于近碍物变步长的策略,生成节点数量较多,虽可以提高路径精细度,但节点之间距离会变得集中,从而增加了冗余节点数量。倒退式去除冗余点通常是在生成节点之后回溯,通过检测障碍物与路径的碰撞,来决定哪些节点冗余。前进式去除中,由于每次生成新节点时就进行碰撞检测,能及时识别并排除冗余节点,减少了整体碰撞检测次数。在复杂环境中,采用前进式冗余点去除方法能够有效减少碰撞检测次数,提高整体算法效率。
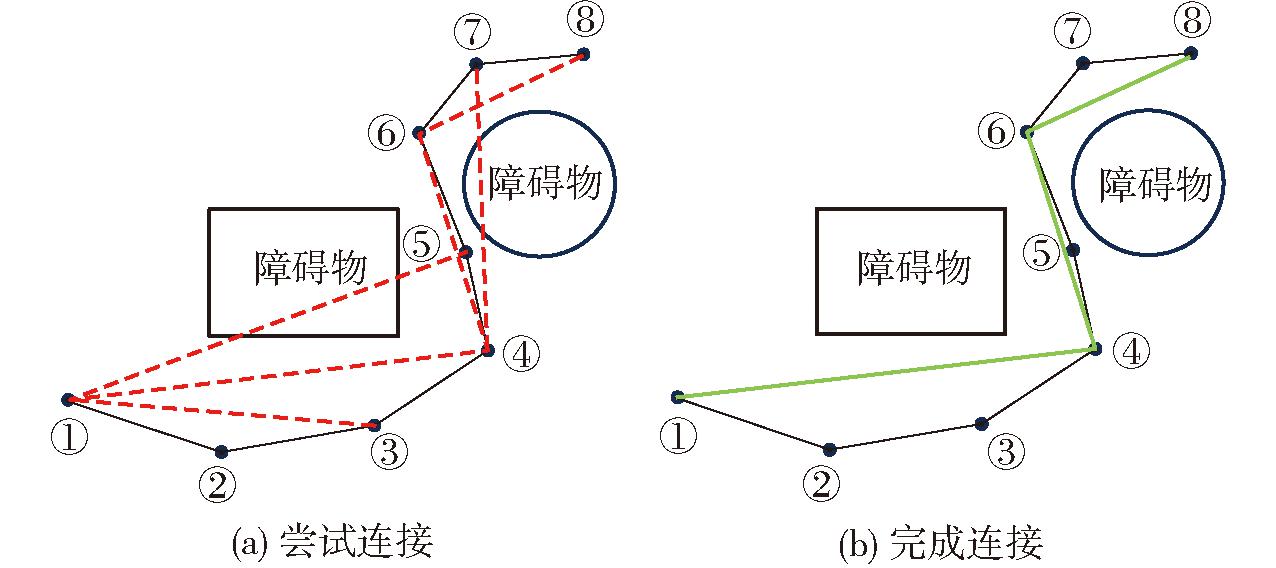
图6 冗余点去除示意图
Fig.6 Schematics of redundant point removal
虽然上述方法对路径中的冗余点进行了有效去除,但生成的路径中还是存在一些拐点,为了解决此问题,接着采用B样条对去除冗余点后的路径进行平滑处理[24]。B样条曲线的平滑性受其次数的影响,次数越高曲线越平滑,但计算复杂度也随之增加。综合考虑曲线平滑度需求、控制点数量以及计算效率,选择三次B样条曲线进行路径平滑处理。三次B样条曲线平滑性强,计算复杂度较低而且具备良好的局部修改特性。
三次B样条曲线基函数为
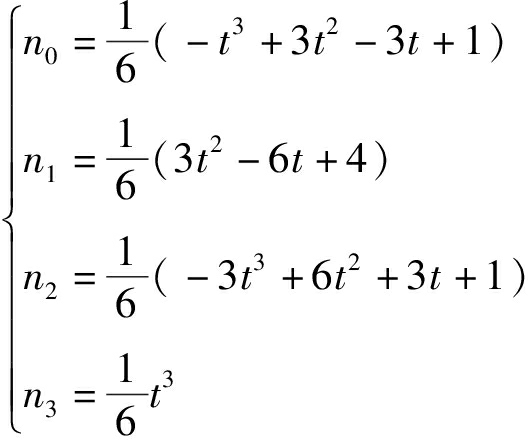
(5)
式中 t——节点
n0、n1、n2、n3——基函数
采用三次B样条对路径中拐点进行平滑处理,路径平滑处理前后效果如图7所示。
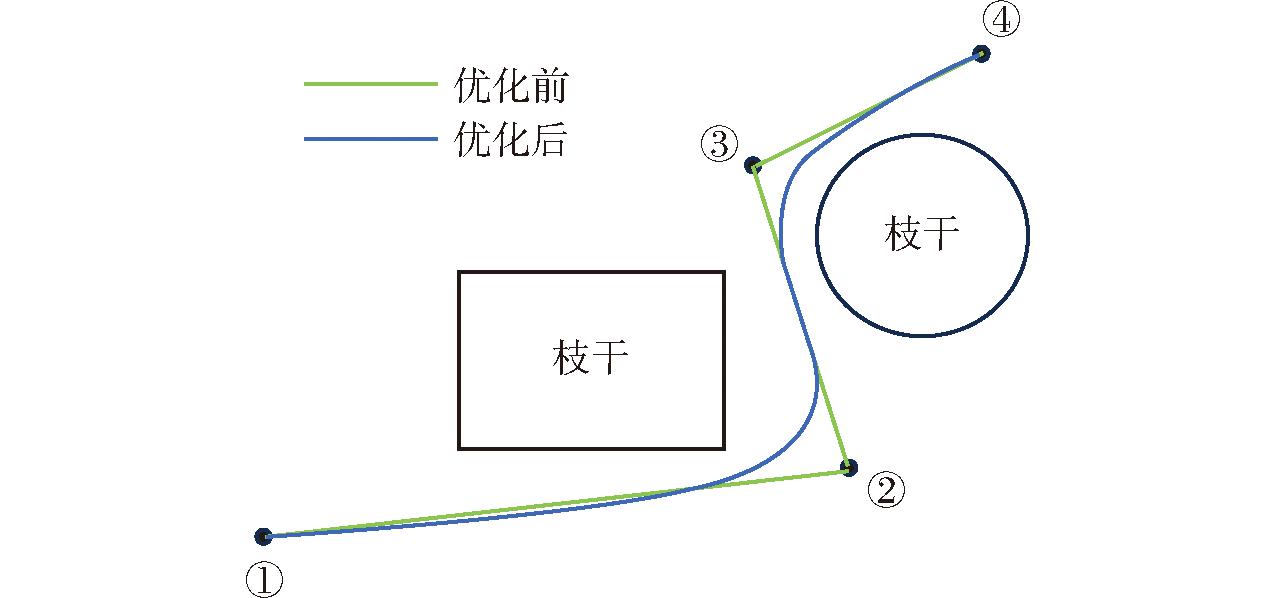
图7 路径平滑处理
Fig.7 Path smoothing processing
粒子群优化(PSO)算法[25]是一种基于群体智能的优化方法,模拟鸟群的觅食行为,适用于多目标优化问题。在优化苹果采摘顺序时,PSO算法首先在搜索空间中随机生成多个粒子,每个粒子表示一个可能的采摘顺序。随后,算法为每个粒子计算适应度,通常基于路径长度、采摘时间等指标。通过考虑粒子历史最佳位置和群体最佳位置,更新每个粒子速度。这一速度用于更新粒子位置,从而生成新采摘顺序。其中速度和位置更新公式为
vi(t+1)=ωvi(t)+c1r1(pbesti-xi(t))+
c2r2(gbest-xi(t))
(6)
xi(t+1)=xi(t)+vi(t+1)
(7)
式中 ω——惯性权重 vi——粒子速度
xi——粒子当前位置
c1、c2——学习因子,取c1=c2=2
r1、r2——介于0~1之间的随机数
pbest——第i个粒子所经过最优位置
gbest——所有粒子经过最优位置
这个循环过程,包括适应度评估、速度和位置更新,会持续进行,直到满足特定的终止条件,例如达到最大迭代次数或适应度变化低于设定阈值。最终,逐步找到更优的苹果采摘顺序,从而提升采摘效率和路径规划效果。
在真实采摘场景中,机械臂往往面临多个目标和约束条件之间的冲突关系。在这种情况下,单一目标求解方法可能无法捕捉复杂性,也无法提供必要的灵活性和最优解[26],此时一般选择由外向内、由近及远的采摘方式,没有对所有目标果实的采摘路径做整体最优规划。考虑空间中的树枝遮挡,枝叶密集程度直接影响路径规划结果,基于粒子群优化算法引入一个树枝密集度参数Ddensity,计算式为
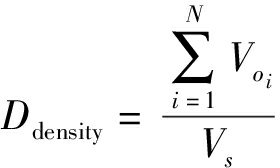
(8)
式中 Voi——单位空间内第i个树枝的体积
N——单位空间内树枝的总数量
Vs——单位空间体积
数值越大表示枝叶越密集。
在采摘环境下确定苹果最优采摘顺序,粒子群中每个粒子表示一种采摘顺序,通过适应度函数评估采摘顺序性能,再通过PSO迭代优化,逐步找到最优采摘顺序,使得总路径最短、时间最优、避开障碍最少。引入树枝密集度参数后适应度函数为
f(x)=L(x)+δ1T(x)+δ2Ddensity(x)
(9)
式中 L(x)——基于采摘顺序计算的路径总长度
T(x)——采摘时间 δ1、δ2——权重
根据PSO算法引入树枝密集度参数Ddensity,优化全局采摘顺序,在确定采摘顺序后使用改进的RRT*算法进行逐个目标点路径规划,从起始点到第1个目标点,再从第1个目标点为起始点到第2个目标点,如此到最后1个目标点按序规划,生成最终路径。苹果采摘环境下多目标采摘路径规划总流程如图8所示。
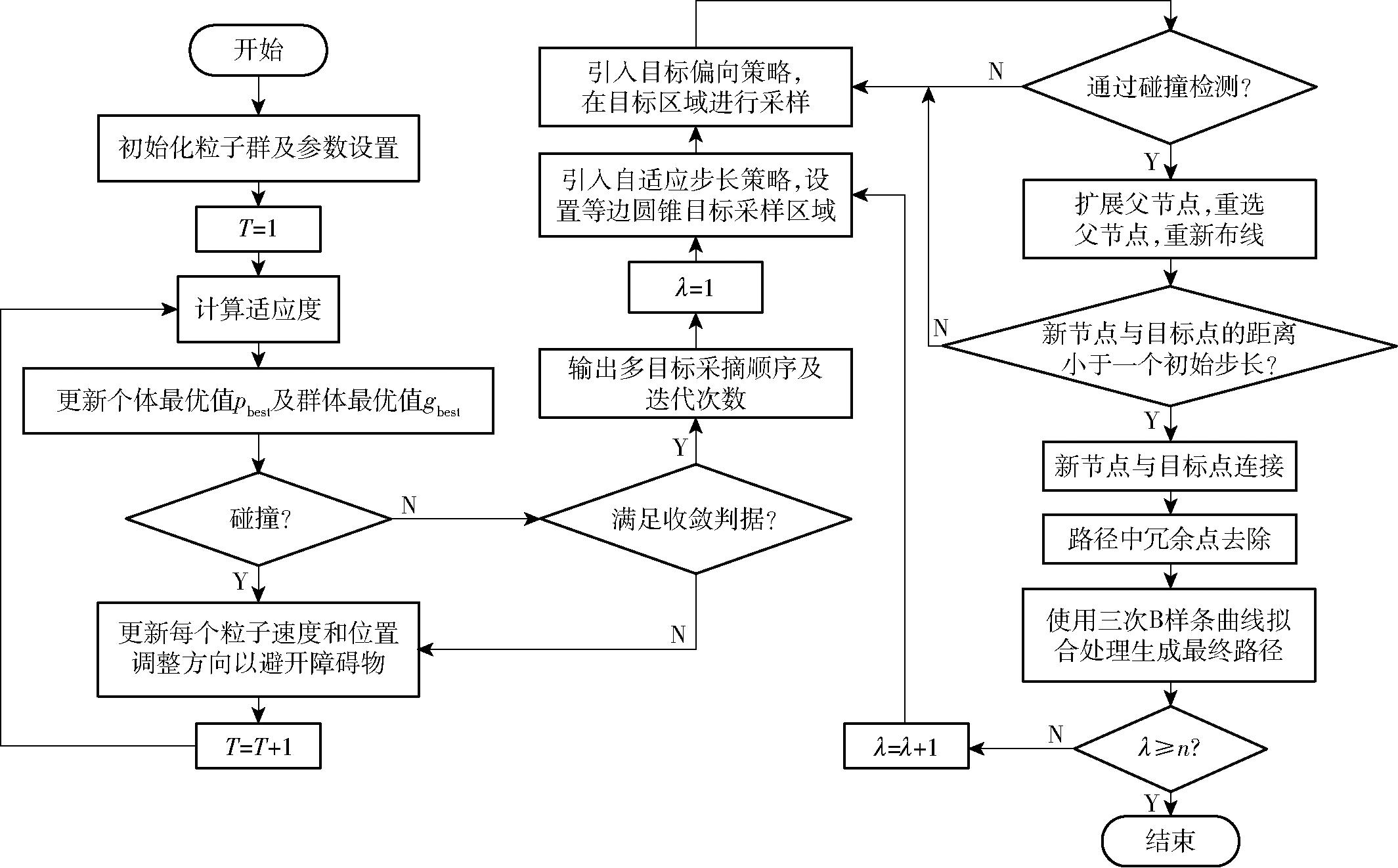
图8 基于目标引导的多目标苹果采摘路径规划流程图
Fig.8 Flowchart of multi-objective apple picking path planning based on target guidance
为了验证多目标苹果采摘路径规划方法在效果和性能上的优越性,在Matlab中进行算法仿真实验,对比分析RRT算法、RRT*算法与TG-RRT*算法结果;PSO算法与TG-RRT*算法结合对比BD-PSO_TG-RRT*算法多目标规划结果。所用的计算机配置包括Windows 11操作系统、i7-9750H CPU处理器,主频2.60 GHz,以及16 GB运行内存。
在真实采摘过程中,采摘工作总是在苹果树四周的某一方向根据采摘机械臂工作空间进行规划。为了使仿真更贴合实际,提取出单面树枝进行仿真实验,根据果实位置设置目标点位置。其中空间尺寸为0.5 m×0.5 m×1 m。初始点坐标(-1,-2,2) m,目标点坐标(2.48,-2.97,8.7) m。在路径搜索过程中,引入目标偏向概率为0.1,迭代次数上限为1 000,每组实验进行100次仿真,取平均值为最终结果。本文将TG-RRT*算法与RRT、RRT*算法进行模型仿真对比实验,仿真结果如图9所示。
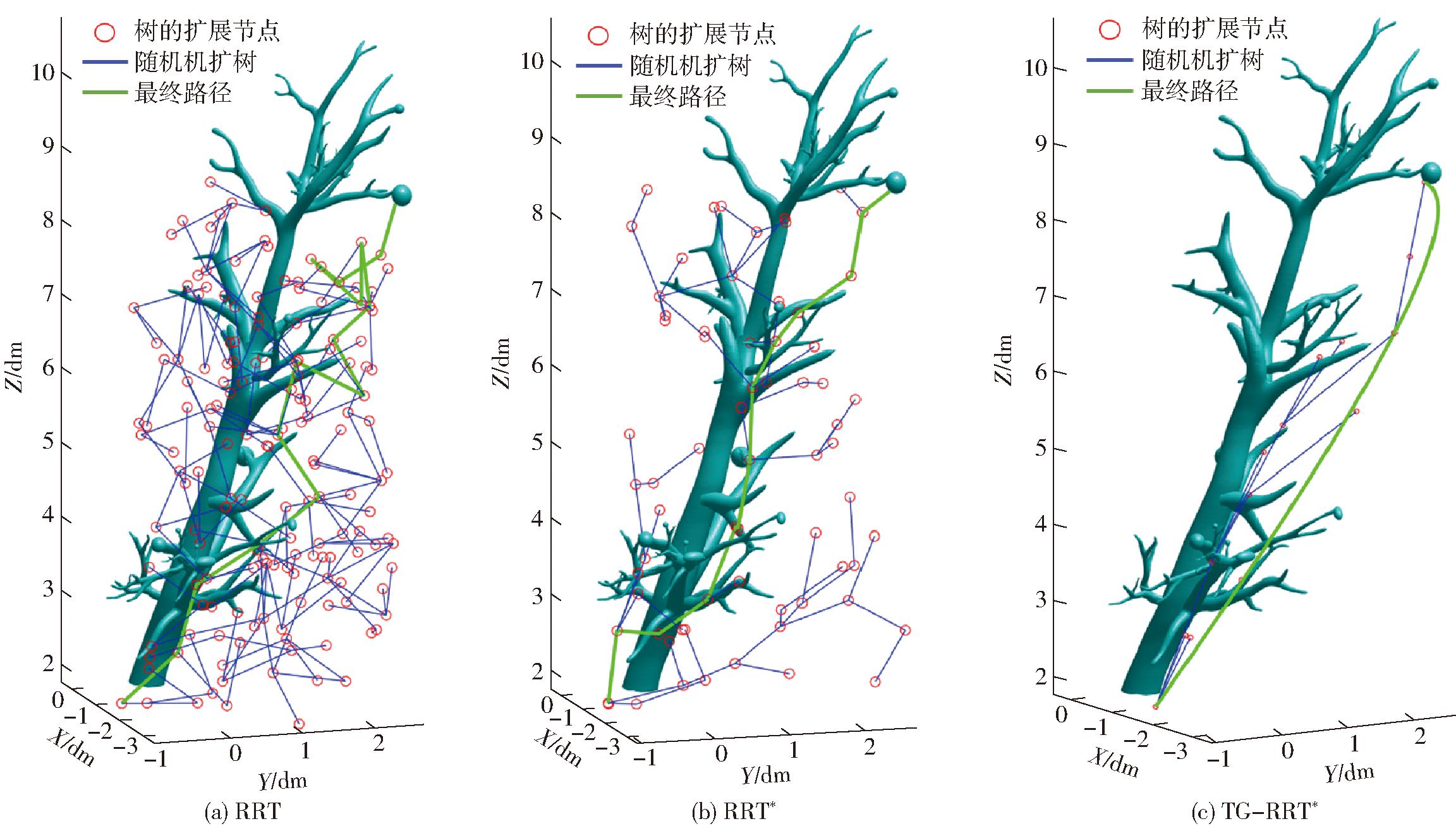
图9 不同算法路径生成结果
Fig.9 Path results generated by different algorithms
表1为3种路径规划算法实验结果,由表1可知,TG-RRT*算法相对于RRT算法平均路径长度缩短23.18%,平均时间降低12.59%,迭代次数降低68.07%。与RRT*算法相比平均路径长度缩短11.67%,平均时间降低71.96%,迭代次数降低31.58%。从图9可以看出,RRT算法与RRT*算法依赖随机生成,迭代生成的路径不够平滑且存在冗余节点。相比之下TG-RRT*算法减小了随机生成范围,使得路径朝目标点方向更新,降低了搜索代价,通过较少的迭代次数使得新节点更接近目标点,减少了计算时间和资源消耗。
表1 路径规划算法实验结果
Tab.1 Experimental results of path planning algorithms
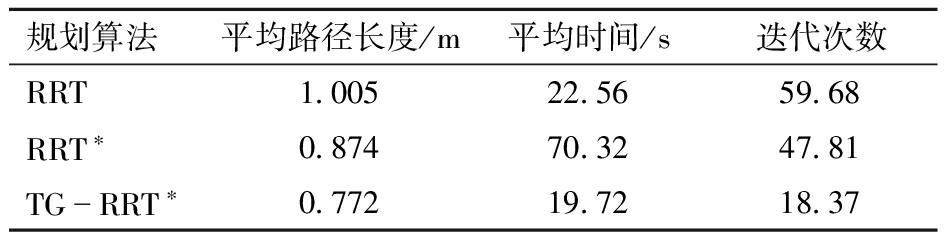
规划算法平均路径长度/m平均时间/s迭代次数RRT1.00522.5659.68RRT∗0.87470.3247.81TGRRT∗0.77219.7218.37
由图10可以看出,从路径长度、时间和迭代次数3方面数据对比,目标引导的RRT*路径规划算法规划效果更好,路径规划长度平均最短,平均时间最短,平均迭代次数最少。
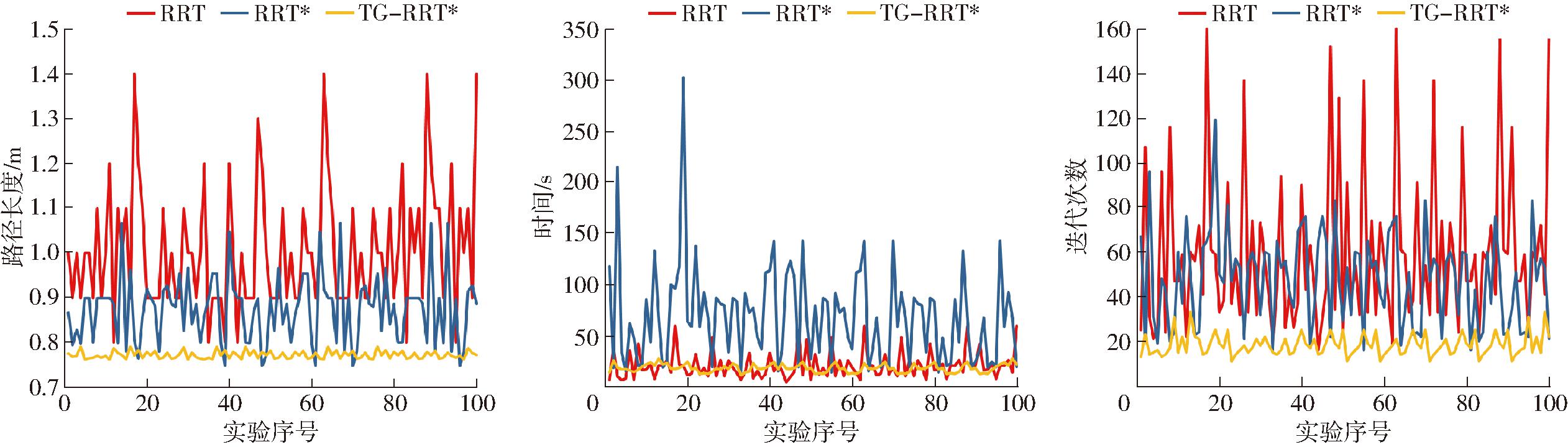
图10 实验数据对比
Fig.10 Comparison of experimental data
为了验证目标引导的多目标苹果采摘路径规划方法的性能,在苹果树模型上选取枝干的6个不同目标,重复规划仿真实验50次,对6个目标点分别采用常规的PSO算法加上改进的RRT*算法(PSO+TG-RRT*)和BD-PSO_TG-RRT*算法进行采摘路径规划,规划结果如图11所示。前者遍历顺序为起始点→4→5→1→3→6→2,后者遍历顺序为起始点→5→4→3→1→6→2,改进前后规划得到的采摘顺序不同,路径轨迹也不同。
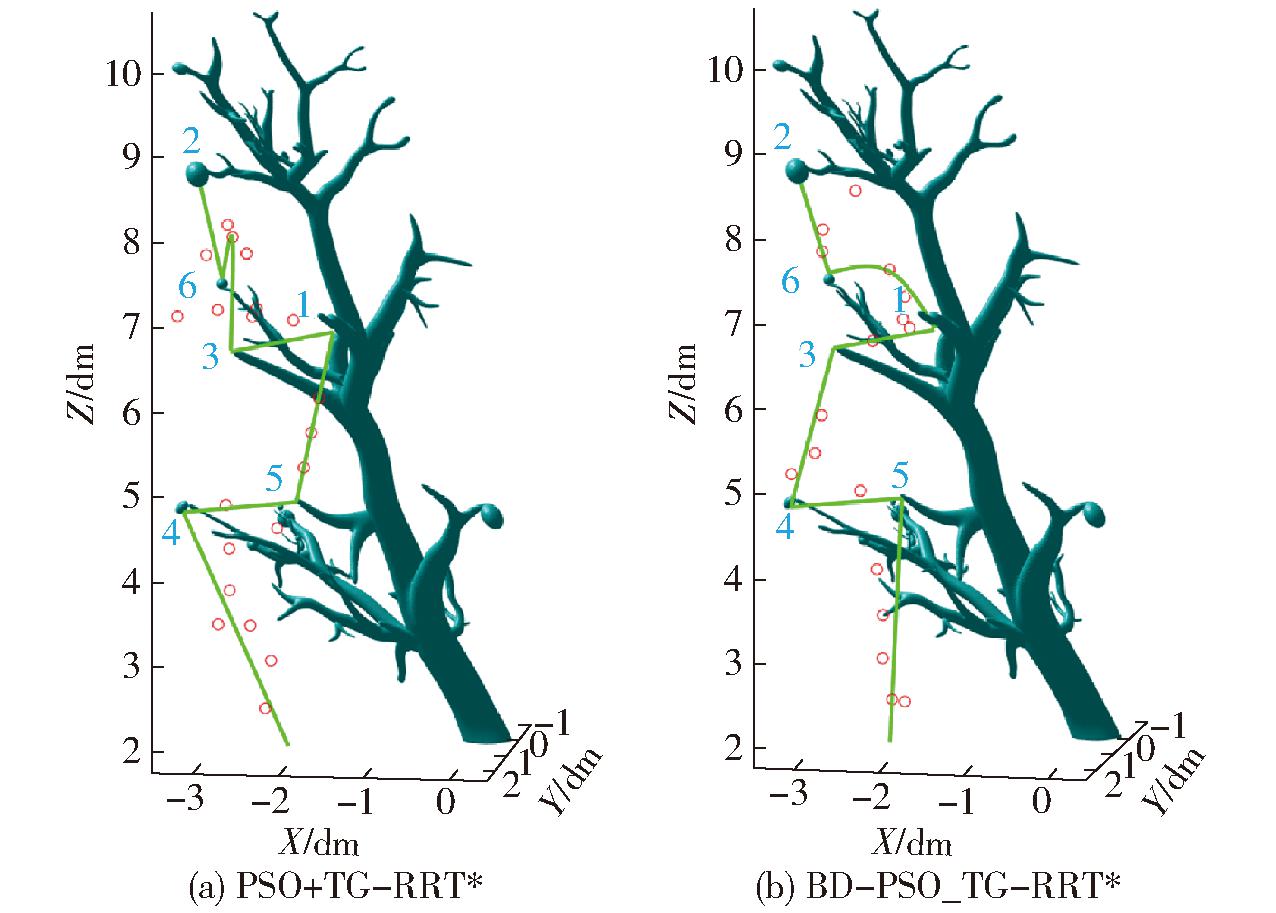
图11 多目标规划路径轨迹
Fig.11 Multi-objective planning path trajectory
表2为多目标连续采摘路径规划仿真实验结果。由表2可以看出,算法改进前后多目标连续采摘路径平均长度相差很小,但平均规划时间降低8.14%,平均迭代次数降低13.24%。原因为改进前后路径规划使用的都是目标引导的RRT*路径规划算法,且各个目标间距离较短,所以规划出的路径轨迹长度变化不大,但因为在PSO算法中引入树枝密集度参数对采摘顺序进行了优化,综合评估了目标点之间的距离与树枝密集度对多目标连续采摘路径的影响,在采摘过程中根据局部枝叶密集度减小了迭代次数,使多目标连续采摘路径规划过程更高效,降低了规划时间。
表2 多目标连续采摘路径规划仿真实验结果
Tab.2 Results of multi-objective continuous planning simulation experiments

多目标连续采摘 路径规划算法多目标连续采摘路径平均长度/m平均规划时间/s平均迭代次数PSO+TGRRT∗1.2261513.280727.64BDPSO_TGRRT∗1.2228812.199123.98
多目标规划路径轨迹实验结果如图12所示。由图12可以看出,在多目标采摘规划中,本文提出的目标引导的多目标采摘路径规划算法过程迭代次数更少,规划时间更短,在多目标采摘过程中采摘效率更高。
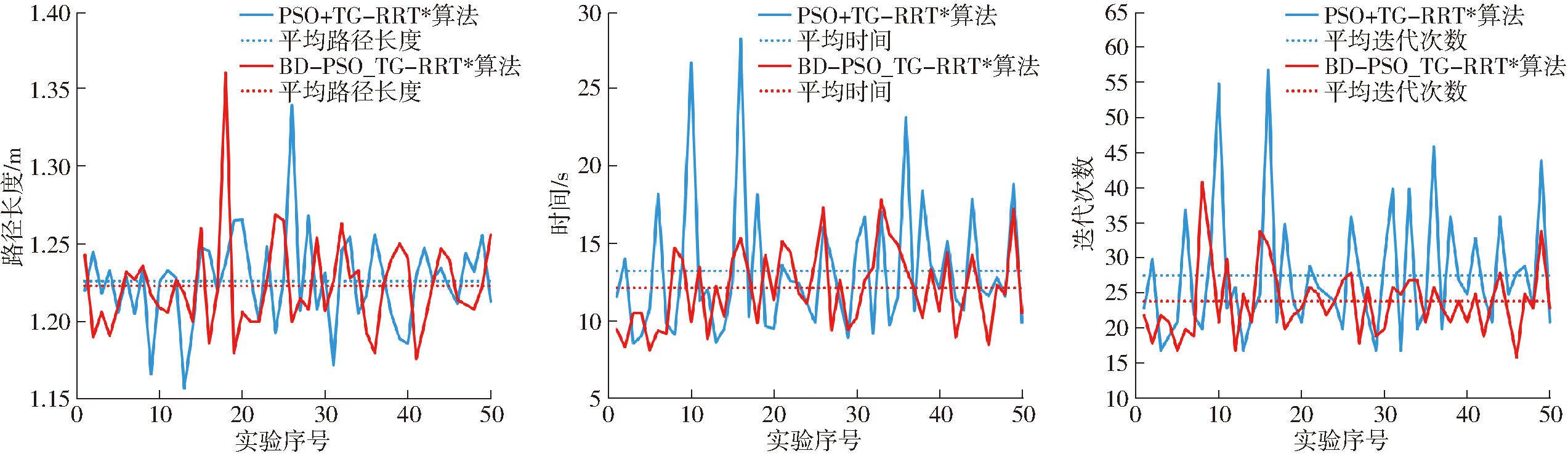
图12 实验结果对比
Fig.12 Comparison of experimental results
(1)针对苹果采摘路径规划问题,提出了TG-RRT*算法进行无碰撞路径规划。该算法提出自适应步长策略,设定等边圆锥的目标采样区域来改进采样过程,剔除冗余点并对路径采用三次B样条曲线平滑处理,提高了路径质量与路径生成效率。通过Matlab仿真对比实验,结果表明该算法相较于传统的RRT和RRT*算法,平均路径长度分别缩短23.18%和11.67%,平均规划时间减少12.59%和71.96%,迭代次数减少68.07%和31.58%。
(2)针对多目标采摘顺序问题,考虑空间障碍物的影响,算法引入带树枝密集度参数的PSO算法优化了采摘顺序。实验结果显示,与原PSO结合TG-RRT*算法相比,BD-PSO_TG-RRT*算法将平均规划时间缩短8.14%,迭代次数减少13.24%。证明该方法提升了路径生成速度,改善了算法的收敛性和路径质量,提高了多目标采摘的规划效率。
[1] TANG Z L,XU L J,WANG Y C,et al.Collision-free motion planning of a six-link manipulator used in a citrus picking robot[J].Applied Sciences,2021,11:11336.
[2] 刘成良,贡亮,苑进,等.农业机器人关键技术研究现状与发展趋势[J].农业机械学报,2022,53(7):1-22,55.LIU Chengliang,GONG Liang,YUAN Jin,et al.Current status and development trends of agricultural robots[J].Transactions of the Chinese Society for Agricultural Machinery,2022,53(7):1-22,55.(in Chinese)
[3] 荀一,李道政,王勇,等.基于VS-IRRT算法的采摘机械臂路径规划[J].农业机械学报,2023,52(2):129-138.XUN Yi,LI Daozheng,WANG Yong,et al.Path planning of picking robot arms based on VS-IRRT algorithm[J].Transactions of the Chinese Society for Agricultural Machinery,2023,54(2):129-138.(in Chinese)
[4] NAZARAHARI M,KHANMIRZA E,DOOSTIE S.Multi-objective multi-robot path planning in continuous environment using an enhanced genetic algorithm[J].Expert Systems with Applications,2019,115:106-120.
[5] AJEIL F H,IBRAHEEM I K,AZAR A T,et al.Grid-based mobile robot path planning using aging-based ant colony optimization algorithm in static and dynamic environments[J].Sensors,2020,20(7):1880.
[6] ZHUANG M,LI G,DING K.Obstacle avoidance path planning for apple picking robotic arm incorporating artificial potential field and A* algorithm[J].IEEE Access,2023,11:100070-100082.
[7] CHEN Y,LUO G,MEI Y,et al.UAV path planning using artificial potential field method updated by optimal control theory[J].International Journal of Systems Science,2016,47(6):1407-1420.
[8] KHATIB O.Real-time obstacle avoidance for manipulators and mobile robots[J].The International Journal of Robotics Research,1986,5(1):90-98.
[9] LUO L,WEN H,LU Q,et al.Collision-free path-planning for six-DOF serial harvesting robot based on energy optimal and artificial potential field[J].Complexity,2018,2018(1):3563846.
[10] YUAN C,ZHANG W,LIU G,et al.A heuristic rapidly-exploring random trees method for manipulator motion planning[J].IEEE Access,2019,8:900-910.
[11] YE L,DUAN J,YANG Z,et al.Collision-free motion planning for the litchi-picking robot[J].Computers and Electronics in Agriculture,2021,185:106151.
[12] LAVALLE S M,KUFFNER J J.Randomized kinodynamic planning[J].The International Journal of Robotics Research,2001,20(5):378-400.
[13] QURESHI A H,AYAZ Y.Intelligent bidirectional rapidly-exploring random trees for optimal motion planning in complex cluttered environments[J].Robotics and Autonomous Systems,2015,68:1-11.
[14] KANG M L,CHEN Q H,FAN Z M,et al.A RRT based path planning scheme for multi-DOF robots in unstructured environments[J].Computers and Electronics in Agriculture,2024,218:108707.
[15] WANG Y,LIU D,ZHAO H M,et al.Rapid citrus harvesting motion planning with pre-harvesting point and quad-tree[J].Computers and Electronics in Agriculture,2022,202:107348.
[16] KIM M C,SONG J B.Informed RRT* with improved converging rate by adopting wrapping procedure[J].Intelligent Service Robotics,2018,11:53-60.
[17] GAMMELL J D,BARFOOT T D,SRINIVASA S S.Informed sampling for asymptotically optimal path planning[J].IEEE Transactions on Robotics,2018,34(4):966-984.
[18] GAMMELL J D,SRINIVASA S S,BARFOOT T D.Informed RRT*:optimal sampling-based path planning focused via direct sampling of an admissible ellipsoidal heuristic[C]∥Proceedings of the 2014 IEEE/RSJ Inter-national Conference on Intelligent Robots and Systems.IEEE,2014:2997-3004.
[19] 熊俊涛,陈浩然,姚兆燊,等.基于PIB-RRTstar的荔枝采摘机械臂运动规划方法[J].农业机械学报,2024,55(10):82-92.XIONG Juntao,CHEN Haoran,YAO Zhaoshen,et al.Motion planning for lychee picking manipulator based on PIB-RRTstar algorithm[J].Transactions of the Chinese Society for Agricultural Machinery,2024,55(10):82-92.(in Chinese)
[20] CAO X M,ZOU X J,JIA C Y,et al.RRT-based path planning for an intelligent litchi-picking manipulator[J].Computers and Electronics in Agriculture,2019,156:105-118.
[21] 栾庆磊,郭继智,屈紫浩,等.改进RRT算法的机械臂路径规划[J].组合机床与自动化加工技术,2024(5):60-64,70.LUAN Qinglei,GUO Jizhi,QU Zihao,et al.Improved RRT algorithm for robotic arm path planning[J].Modular Machine Tool &Automatic Manufacturing Technique,2024(5):60-64,70.(in Chinese)
[22] 孟月波,张子炜,吴磊,等.目标区域引导的RRT*机械臂路径规划算法[J].计算机科学与探索,2024,18(9):2407-2421.MENG Yuebo,ZHANG Ziwei,WU Lei,et al.Target area guided manipulator path planning of RRT*[J].Journal of Frontiers of Computer Science and Technology,2024,18(9):2407-2421.(in Chinese)
[23] WANG Y,JIANG W S,LUO Z,et al.Path planning of a 6-DOF measuring robot with a direction guidance RRT method[J].Expert Systems with Applications,2024,238:122057.
[24] 刘小松,康磊,单泽彪,等.基于双向目标偏置APF-informed-RRT算法的机械臂路径规划[J].电子测量与仪器学报,2024,38(6):75-83.LIU Xiaosong,KANG Lei,SHAN Zebiao,et al.Robotic arm path planning based on two-way target bias APF-informed-RRT algorithm[J].Journal of Electronic Measurement and Instrumentation,2024,38(6):75-83.(in Chinese)
[25] KIM J J,LEE J J.Trajectory optimization with particle swarm optimization for manipulator motion planning[J].IEEE Transactions on Industrial Informatics,2015,11(3):620-631.
[26] LI X,LV H,ZENG D T,et al.An improved multi-objective trajectory planning algorithm for kiwifruit harvesting manipulator[J].IEEE Access,2023,11:65689-65699.