0 引言
农业示范园区由于标准化栽培模式和示范效应,使得农业机器人开始逐步得到应用,例如采摘机器人、巡航机器人和喷药机器人等。实现农业机器人[1]自主作业的关键技术之一就是路径规划,其主要包括行间行走和转行调头。在农业示范园区作业时转行调头进入其他垄行的行程中,所经过的通道大都为宽敞的共同作业通道。这些通道不仅被用作游客参观路径,也是工人进行日常作业的通道。通道常常会出现移动频繁的障碍物,如人员和工具车等,同时,也会有采集桶、指示牌等活动性较小的障碍物存在。因此,为在这个作业环境下进行精确导航与避障,高效的局部路径规划算法非常必要。常见的局部路径规划[2]方法有:人工势场法[3]、D*算法[4]、蚁群算法[5-6]、时间弹性带算法[7]及动态窗口法[8-9]等,但这些算法在应对机器人行走时出现的不同类型的动态障碍物都存在一定适应性问题。
动态窗口法(Dynamic window approach,DWA)是一种高效且实时的局部路径规划算法,适用于动态环境下的机器人,可以快速做出决策,高效计算路径,生成平滑的移动轨迹,同时算法的实现相对简单直观。然而,动态窗口法也有其局限性[10],如可能陷入局部最小值,依赖对周边环境的感知能力,需要经过精细调整,才能在不同场景下达到最佳性能,且在高度动态环境时有局限性。
文献[11-13]对DWA算法进行了改进,但改进方法没有考虑动态障碍物的随机性,动态避障能力弱。文献[14-16]研究可显著提升路径规划效果,但整体寻路时间较慢,运行时间较长,无法对未知障碍物做到实时反馈且无法用于多特殊障碍物组合的场景。
综上,为提高对动态障碍物行为随机性的重视程度,更好地完成动态避障,以及避免陷入局部最小值,本文提出基于双障碍物评价函数、自适应权重和虚拟目标法的动态窗口法(Dual obstacle cost function,adaptive weights and virtual target_dynamic window approach,DAV_DWA)。首先,对动态和静态障碍物采用不同的评价方法,以解决动态障碍物处理不当的问题;其次,将各评价函数的权重根据模糊逻辑算法实现自适应调整,解决目标不可达、无法选择较短路径等问题;最后,引入虚拟目标点,使其行驶至局部最小值后仍可脱困。通过仿真试验和温室障碍物环境下试验,检验算法在导航任务中的实用性。
1 传统DWA算法
DWA算法是机器人领域广泛应用于局部路径规划问题的一种经典算法[17],该算法在速度(v,ω)空间内采样多组速度,并进一步模拟这些速度下一步形成的轨迹,算法评估这些速度对应的不同轨迹,并选择最佳轨迹以指示机器人行动,实现即时而有效的导航决策。
1.1 履带机器人运动模型分析
本文模型为履带差速运动模型,为非全向运动模型,机器人只能前进或转向,如图1所示。
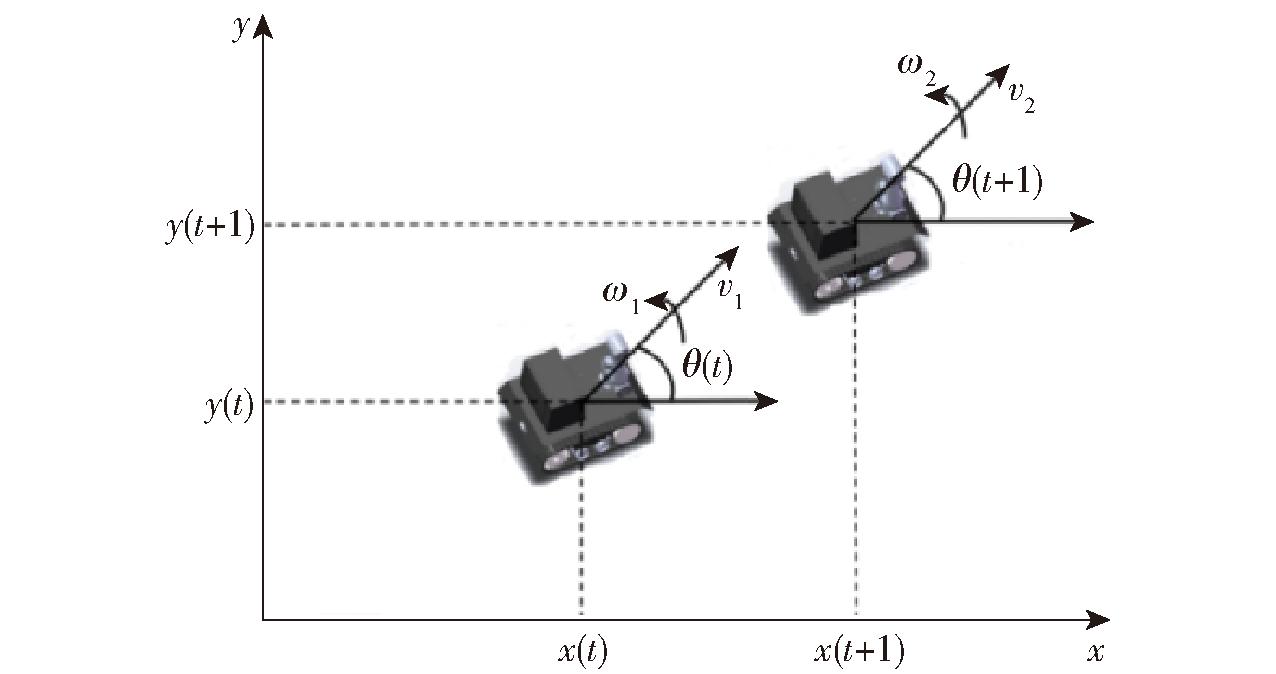
图1 机器人运动模型分析
Fig.1 Analysis of motion model of robot
如图1所示,假设机器人从t时刻运行到t+1时刻,运动距离极短,机器人在相邻2个时刻运动方程为
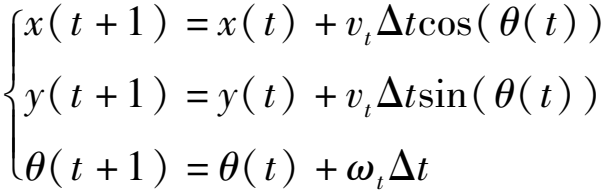
(1)
式中 Δt——相邻2个时刻时间差
vt——Δt内瞬时线速度
ωt——Δt内瞬时角速度
x(t)、y(t)——t时刻坐标值
x(t+1)、y(t+1)——t+1时刻坐标值
θ(t)——t时刻方向角
在DWA算法中,通过不断更新vt和ωt,即可计算出机器人在整个仿真周期内的位置和方向角。
1.2 机器人速度采样空间
根据机器人情况,动态窗口法需要考虑机器人当前速度以及与障碍物交互时可能的速度变化,来实时地选择一条最优路径。合理定义速度范围、考虑机器人动态约束和环境约束,对实现高效和安全的路径规划至关重要。
(1)速度范围:指机器人前进时线速度和角速度最大值与最小值[18]。
vm={(v,ω)|v∈(vmin,vmax),ω∈(ωmin,ωmax)}
(2)
式中 vm——机器人速度范围
v——机器人线速度 ω——机器人角速度
(2)动态约束:指机器人在电机性能等限制下,加速度能达到的最大值。
(3)
式中 vd——机器人在动态约束下速度范围
vc、ωc——机器人当前线速度和角速度
![]() 机器人最大线加速度和最大角加速度
机器人最大线加速度和最大角加速度
(3)环境约束:为了防止发生碰撞,需要合理限制机器人速度空间[19]
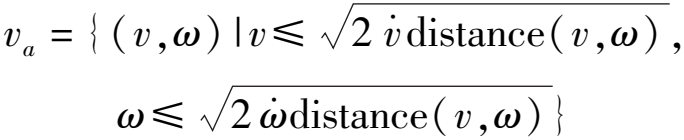
(4)
式中 va——机器人在环境约束下速度
distance(v,ω)——机器人模拟轨迹上与障碍物的最近距离
![]() 机器人最大线减速度
机器人最大线减速度
![]() 机器人最大角减速度
机器人最大角减速度
最终速度范围为以上3个速度集合,满足
v=vm∩vd∩va
(5)
1.3 轨迹评价函数
DWA算法中轨迹评价函数表达式为
G(v,ω)=σ(αheading(v,ω)+βdist(v,ω)+
γvelocity(v,ω))
(6)
式中 heading(v,ω)——方位角评价函数。在特定速度下,机器人预计轨迹终点的朝向与目标位置之间的角度偏差[20]
dist(v,ω)——机器人轨迹到障碍物距离评价函数
velocity(v,ω)——当前机器人线速度[21]评价函数
α、β、γ——方位角函数、障碍物函数和速度函数权重
σ——归一化处理参数,对以上评价函数进一步归一化处理,使得最后可以定位到满足避障、快速到达终点条件的最佳路径
2 DAV_DWA算法
根据机器人传感器信息实时更新静态障碍物、动态障碍物位置。针对路径规划算法对于障碍物避让能力、路径寻优能力及逃脱局部最小值能力要求,针对DWA算法进行以下改进。
2.1 动静障碍物距离评价函数
在温室环境中,不同类型障碍物对于机器人的影响程度也不相同,工作人员、工具车等易于活动的物品对于机器人的威胁程度较大;而采集桶、指示牌等不易于移动的物品对机器人的威胁程度较小,当机器人遇到此类障碍时,相同的避障策略便不再适用。因此将动、静障碍物划分为2个评价函数,从而找到更优的路径,使机器人路径执行效率更高。
DAV_DWA算法在原始动态窗口法评价函数的基础上,将原有评价函数中考虑的距离因素dist(v,ω)细化为2个独立的分量:与动态障碍物之间的距离dist_dynamic(v,ω)和与静态障碍物之间的距离dist_static(v,ω)。
对于这2类不同性质的障碍物,本文算法设定了区别化的安全阈值,并依照障碍物的性质采取相应的避障策略[22]。具体来说,该算法并未过度提高对于静态障碍物的警觉性,避免因绕行静态障碍物而造成额外时间损失;同时,提高了对动态障碍物的重视程度,确保遇到动态障碍物时能够持续保持足够的安全距离。评价函数表达式为
G(v,ω)=σ(αheading(v,ω)+γvelocity(v,ω)+
β1dist_dynamic(v,ω)+β2dist_static(v,ω))
(7)
式中 β1、β2——动、静态障碍物函数权重
2.2 自适应权重参数
通常情况下,传统DWA算法中权重系数是固定的,不能适应机器人在复杂多变的环境中路径规划需求。为了保证机器人在不同的条件下都能找到最优的行驶路线,必须选取合适的加权系数。因此,本文提出在算法中加入模糊逻辑算法,以动静态障碍物距离作为输入,动态调整4个评价函数权重。
模糊逻辑算法主要用于处理和推理不确定性或模糊性的数据,主要步骤分为输入数据模糊化、制定规则库、推理模糊集合和结果去模糊化。依据研究设计要求,本文构建了模糊控制器,该控制器由3个主要组成部分构成:输入变量、控制逻辑规则以及输出响应。输入变量采用Z型隶属度函数、高斯隶属度函数和S型隶属度函数,这3种隶属度函数经常配合用于描述一些连续性较强的现象,能较好地形容控制器中距离值的变化。输出变量采用三角形隶属度函数,其对于权重系数输出具有较好的灵活性。输入变量包含2个关键维度,机器人与动态障碍物的最小距离ObstacleDist_Dynamic和机器人与静态障碍物之间的最小距离ObstacleDist_Static,如图2a、2b所示。
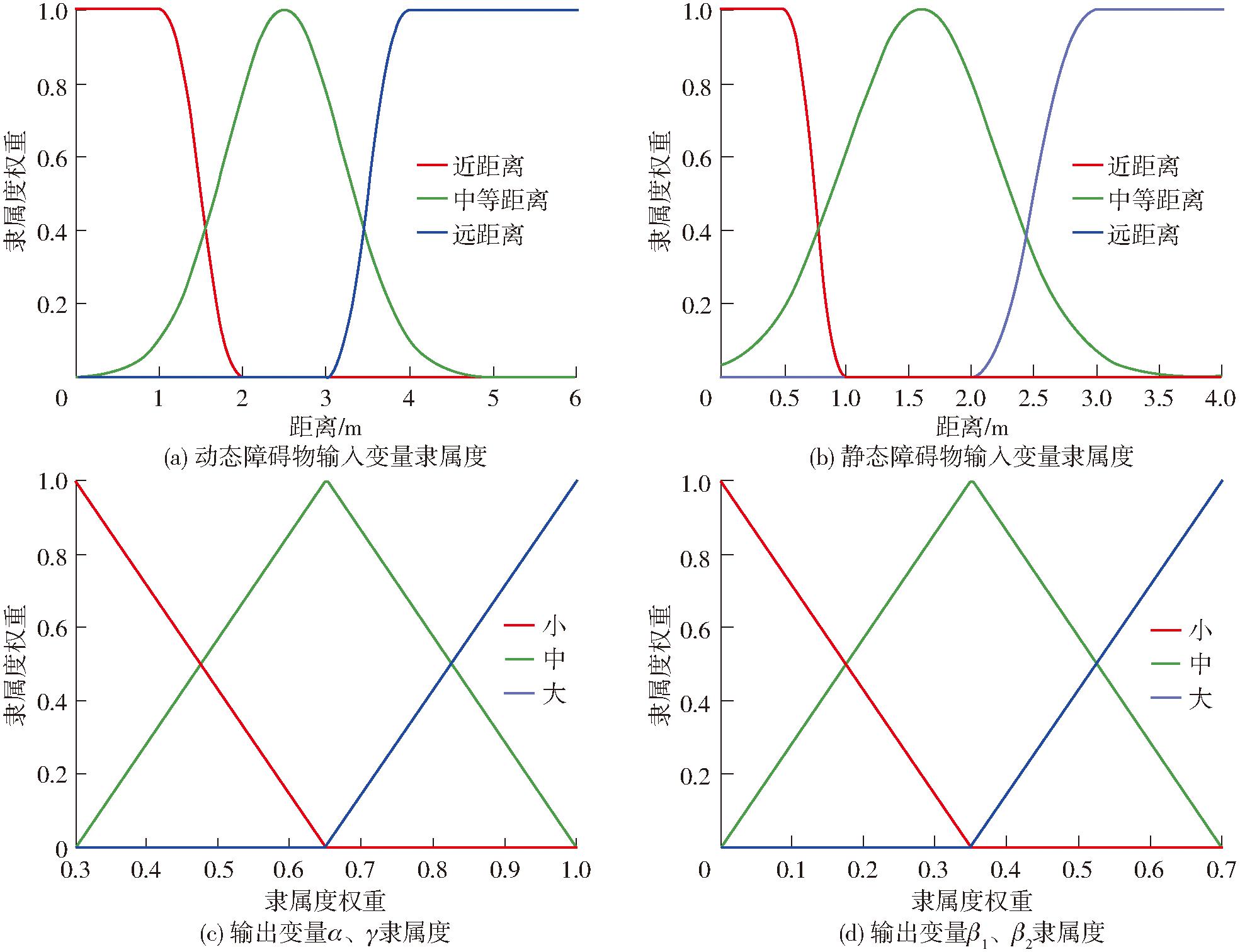
图2 隶属度函数
Fig.2 Affinity functions
输入变量模糊集针对动态及静态障碍物分别定义为{N,M,F},表示近距离、中等距离与远距离,且隶属度参数范围选取主要考虑以下几点:
(1)试验测距所用Intel RealSense D435i型相机在测量固定距离时会产生误差,6 m时误差为0.14 m,7 m时误差为0.21 m,已超过0.20 m,精度已不满足实际应用,所以动态障碍物论域为[0,6 m]。且静态障碍物的威胁程度相对较小,所以论域为[0,4 m]。
(2)行人为场景主要动态障碍物,机器人中心与边缘最大距离计及人的最小社交距离大于1 m,所以第1个Z型隶属度函数为[1 m,2 m];第2个高斯隶属度函数参考人的安全社交距离,以2.5 m为中心;第3个S型隶属度函数参考人的公众距离,定义为[3 m,4 m]。
(3)静态障碍物中第1个Z型隶属度函数参考机器人中心与边缘最大距离,定义为[0.5 m,1 m];第2个高斯隶属度函数选择略低于动态障碍物的威胁距离,以1.6 m为中心;同理,第3个S型隶属度函数为[2 m,3 m]。
控制规则部分负责根据输入变量的评估来形成特定的输出响应;输出部分为4个评价函数权重,记为α、β1、β2和γ,为保证导航路径始终朝向终点,方位角和速度隶属度函数不能太小,同时障碍物权重不宜过大,所以α和γ隶属度函数定义在[0.3,1]区间;β1和β2隶属度函数定义在[0,0.7]区间,如图2c、2d所示。输出变量模糊集定义为{S,M,B},分别对应于小、中、大权重。
此外,本文路径规划的原则是当接近障碍物时,优先执行避障操作。基于此,模糊规则为:
(1)相对于静态障碍物,动态障碍物被认为具有更高的威胁等级和更大的威胁范围。因此,在动态障碍物的评估中,速度和方向角的函数权重被赋予较低的值。
(2)当动态障碍物为最近距离范围时,无论静态障碍物距离远近,小车均选取最小速度,朝着远离障碍物的方向,缓慢避让障碍物。
(3)当动态障碍物与静态障碍物均较远时,障碍物威胁程度最低,小车以较快速度朝着目标点方向前进。
(4)动态障碍物与静态障碍物权重分别根据其距离划分小、中、大等级。
基于以上规则,制定的模糊规则如表1所示。
表1 模糊控制规则
Tab.1 Fuzzy control rule

规则 序号 输入 输出 动态障碍 物距离 静态障碍 物距离 α β1 β2 γ 1 F F B S S B 2 M M M M M M 3 M F M M S M 4 F M M S M M 5 N M S B M S 6 N F S B S S 7 F N M S B S 8 N N S B B S 9 M N S M B S
2.3 虚拟目标法
在传统动态窗口法中,C型障碍物的处理尤为困难[23],主要是因为DWA容易陷入局部最小值,且其短期规划的本质和对环境的感知限制导致机器人可能误入C型障碍物内部而难以脱困,如图3所示。这种算法依赖于机器人当前的感知能力和即时运动状态来评估可能的运动轨迹,而对于复杂的C型障碍物,传统DWA因其短视行为和动态窗口的计算局限性,往往无法准确预测和规避长期潜在的陷阱。
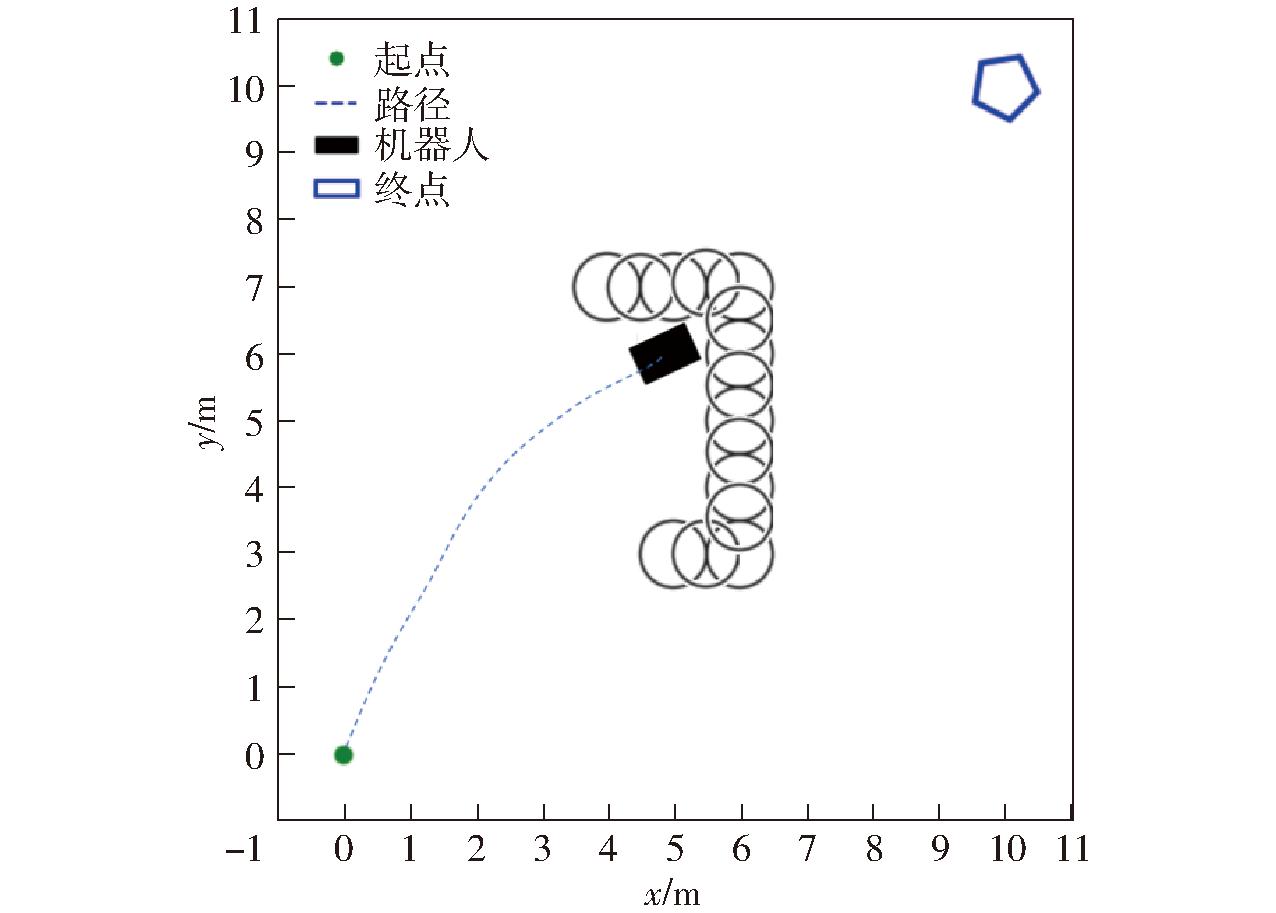
图3 机器人局部最小值图
Fig.3 Robot local minima diagram
为了克服这一困难,本文提出了一种改进策略——虚拟目标法。通过创建虚拟目标点,目的是为了让机器人能够规避那些可能导致陷入局部最小值的情形,有效避开多个障碍物聚堆形成的障碍物区(诸如C型)带来的困扰。具体步骤如下:
(1)当机器人运动速度低于预定的阈值且该状态持续时间超过特定时长,则判定其处于局部最小值位置。
(2)分析机器人附近障碍物分布情况,检测相邻障碍物之间距离小于等于2p(p为机器人半径)的障碍物则添加进一个局部最小值障碍物群中。
(3)选择障碍物群中最外侧且距离机器人较近的障碍物为目标障碍物,在机器人与障碍物连线方向上外侧,距离障碍物2p的地方设置虚拟目标点,如图4所示。
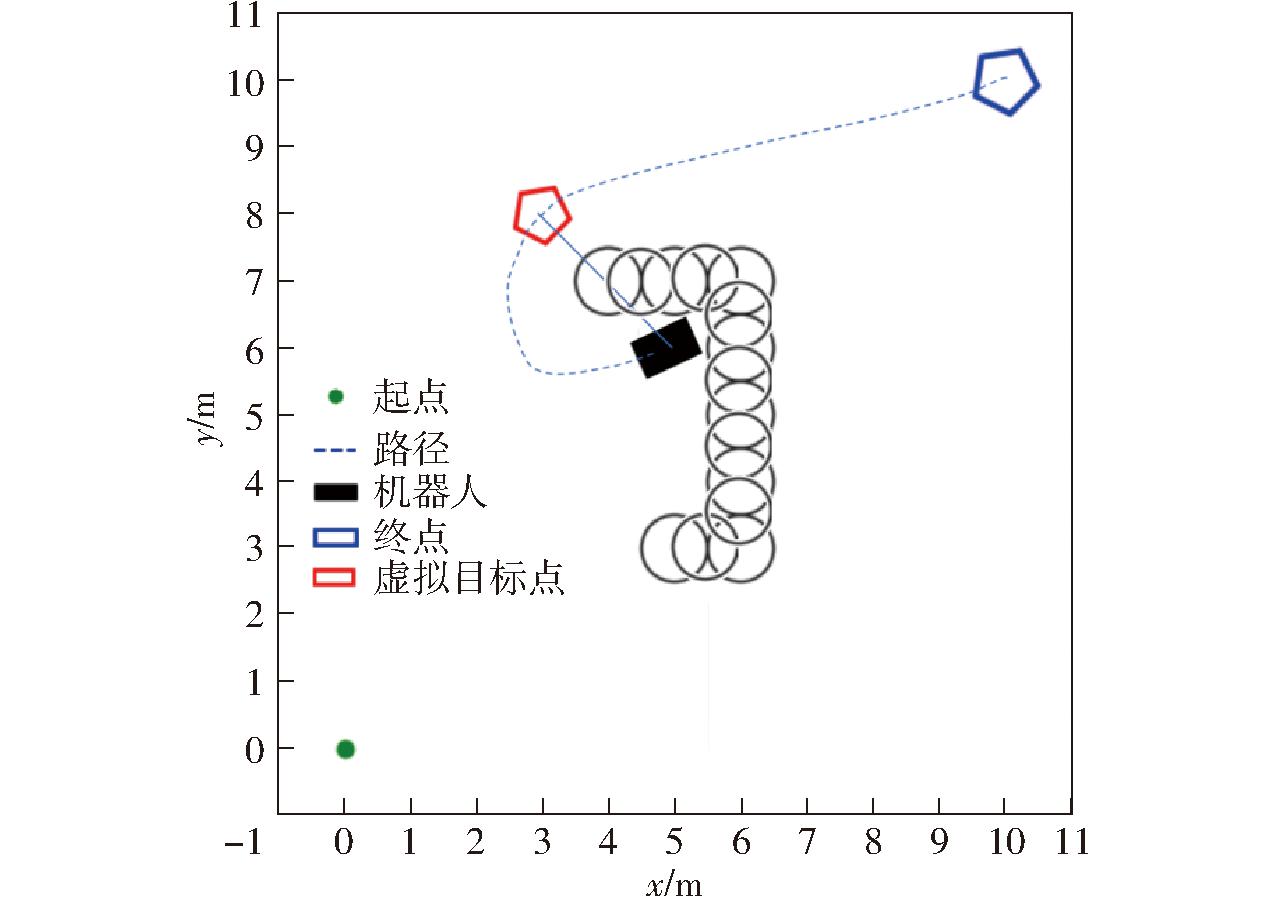
图4 机器人虚拟目标点原理图
Fig.4 Robot virtual target point schematic
(4)若机器人到达虚拟目标点,则将虚拟目标点换成实际目标点;若机器人到达的目标为实际目标点,则算法结束[24]。
3 仿真试验
为了评价DAV_DWA算法的有效性,仿真试验中基于3种场景(场景1、2、3)参照对比原始DWA算法和文献[11]算法进行局部路径规划验证,评价指标为:
(1)安全距离:在仿真过程中机器中心点与障碍物的最小距离,反映算法安全性。
(2)寻路时间:算法完成整个路径规划任务所需的总时间,用来衡量算法效率。
(3)路径长度:从模拟环境起始点(即机器人当前位置)至目标位置所需经过的总距离,反映路径寻优能力。
仿真过程中机器人参数为:最小线速度0 m/s;最大线速度1 m/s;最大线加速度0.4 m/s2;最小角速度0(°)/s;最大角速度20(°)/s;最大角加速度20(°)/s2;机器人中心与边缘最大距离0.5 m。其中DWA的权重参数根据动态障碍物的危险性及路径的寻优能力,方位角评价函数、障碍物距离评价函数、速度评价函数权重分别调整为0.4、0.3、0.3,其他系数为:时间分辨率0.1 s、线速度分辨率0.01 m/s、角速度分辨率1.0(°)/s、预测周期3 s。
首先根据场景1、2,对传统DWA算法、文献[11]算法和DAV_DWA算法的仿真结果进行分析对比,表2为各评价指标的数据。再设置场景3为C型障碍物区域,检测几种算法的脱困能力。
表2 评价指标
Tab.2 Data for evaluation indicators

场景 算法 路径长 度/ m 寻路时 间/ s 与障碍物距 离/ m 传统 DWA 16. 58 18. 9 0. 51 场景 1 文献[11]算法 20. 64 29. 0 0. 78 DAV_DWA 15. 11 18. 0 0. 55 传统 DWA 31. 67 34. 1 0. 11(发生碰撞) 场景 2 文献[11]算法 36. 14 39. 1 0. 52 DAV_DWA 33. 38 35. 6 0. 78
文献[11]算法输入输出均采用高斯隶属度函数,输入量为与障碍物距离、与目标点距离和偏移角,输出量为方位角函数、速度函数和障碍物距离函数的权重。
在场景1中,安全距离为机器人中心与静态障碍物中心距离;场景2中,安全距离为机器人中心与动态障碍物中心距离。当障碍物距离小于等于0.5 m时即发生碰撞。
3.1 场景1(静态障碍物密集随机分布的复杂环境)
在试验中,随机设置1组静态障碍物。采用传统DWA算法、文献[11]中改进DWA算法与DAV_DWA算法进行比较,仿真结果如图5、6所示。
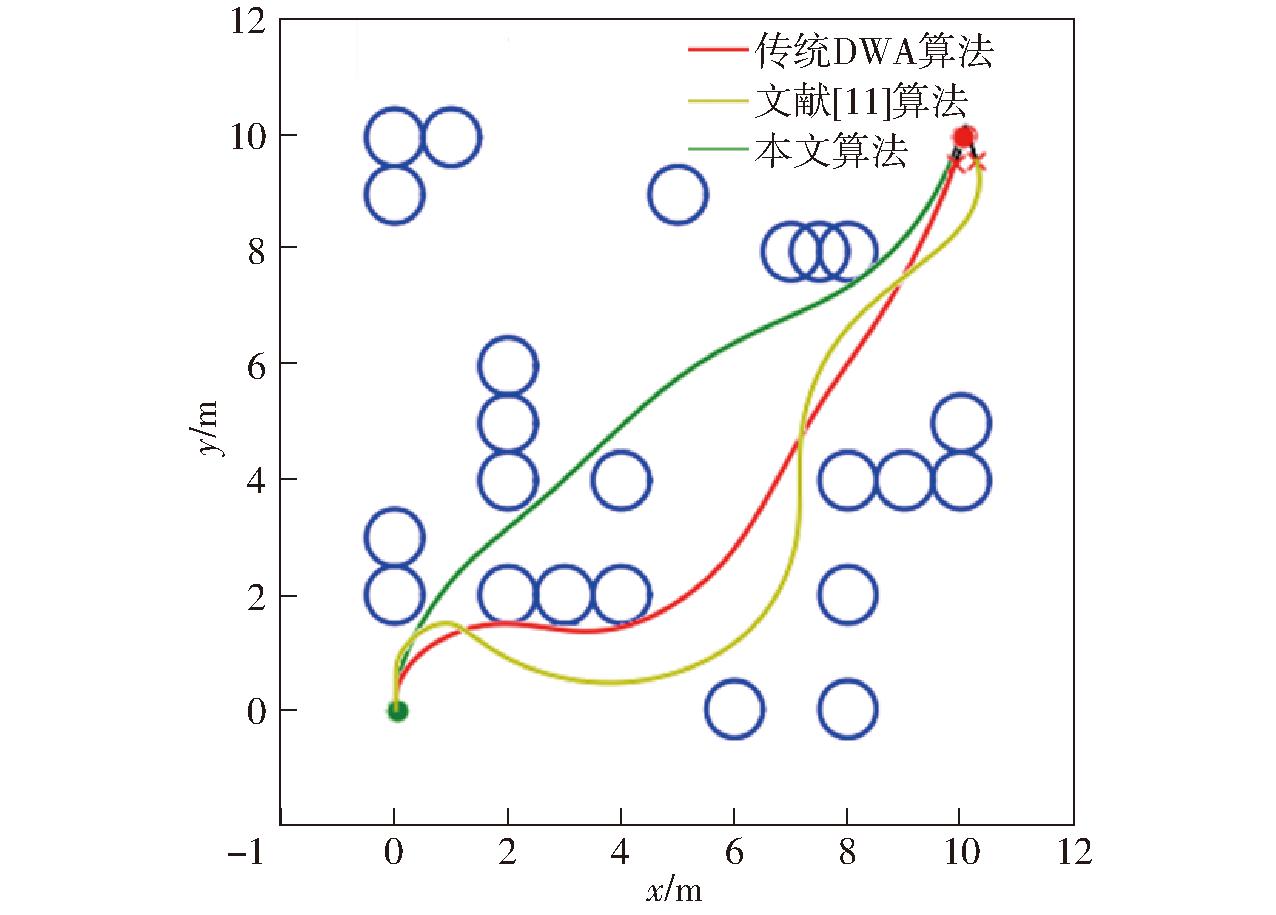
图5 不同算法完整路径图
Fig.5 Complete path diagram of different algorithms
根据图6各种算法的权重变化进行分析,传统DWA算法权重不能根据具体情况调整,存在局限性;文献[11]算法在遭遇静态障碍物时速度与方位角权重大大降低,使之增加路径长度去大幅度绕行,效率较低。本文算法权重通过一定限制后,适当提升对静态障碍物的重视程度,但仍朝着目标点方向且路径较为顺滑,综合考虑最优。
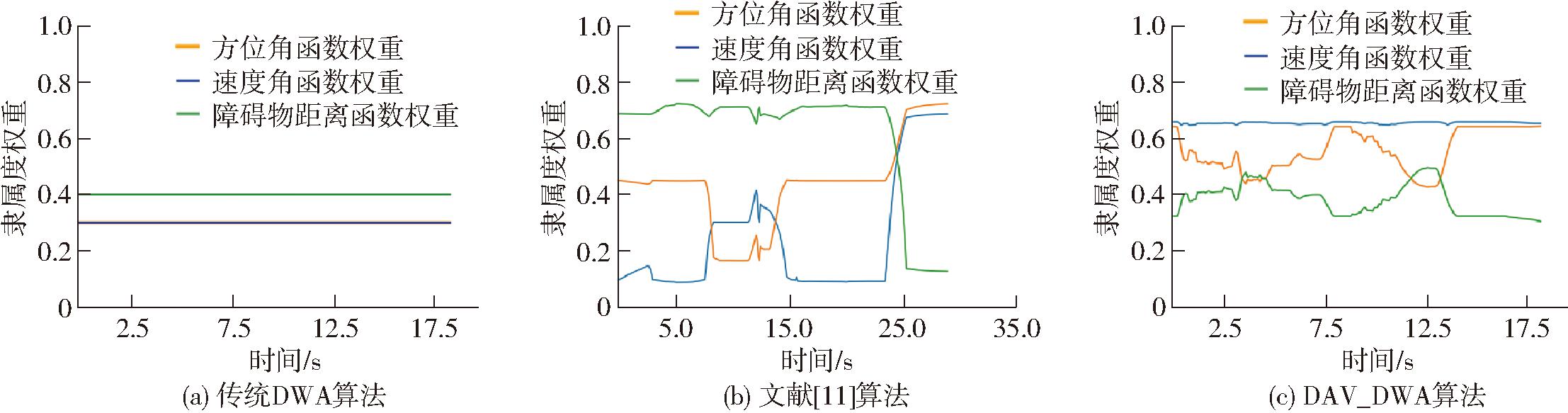
图6 不同算法权重变化曲线(场景1)
Fig.6 Plots of change in weights of different algorithms (Scenario 1)
根据表2和路径对比图的数据分析,路径长度较传统算法减少8.9%,较文献[11]减少26.8%;寻路时间较传统算法减少4.8%,较文献[11]减少37.9%。传统DWA算法在寻找最短路线时,不能很好地保证与静止的障碍物之间的安全距离,这就大大提高了车辆的碰撞风险;文献[11]算法能与障碍物保持较大距离,安全性较好,然而,由于该算法存在选取过度安全距离而无法有效选取最短路径的问题,从而增加了搜索时间和路径长度;DAV_DWA算法在兼顾较短路径的同时选取适当安全距离,实现了寻路时间的最小化以及路径长度的最优化。综合对比,本文算法综合平衡了路径长度与安全性两大关键因素,成功实现了最佳导航路径的选取。
3.2 场景2(静态、动态并存,障碍物密集随机分布的复杂环境)
在本试验中,进一步验证对动态障碍物的处理,在仿真环境中增设4个移动障碍物,障碍物位置及运动方向如图7所示,各种算法仿真结果如图8~11所示。
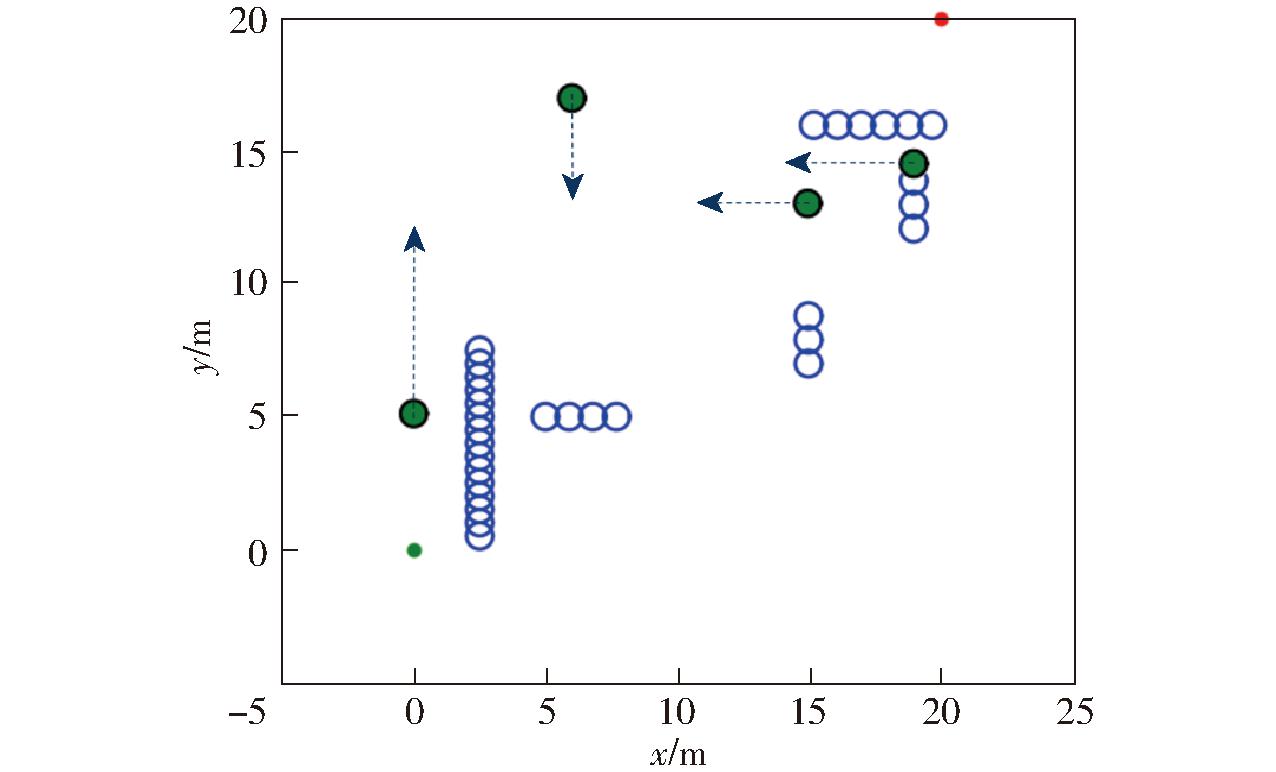
图7 复杂动静障碍物分布图
Fig.7 Distribution of complex static and dynamic obstacles
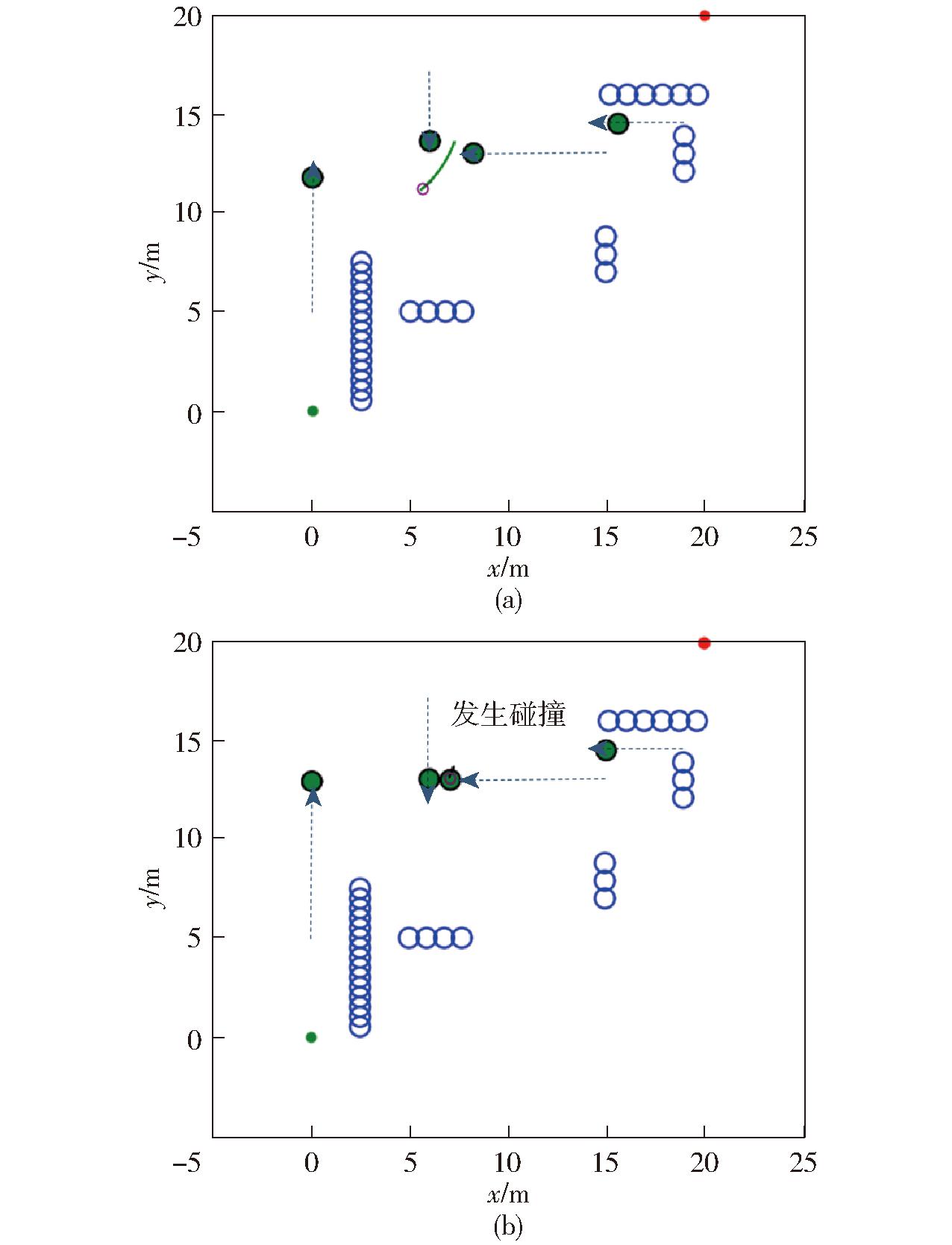
图8 传统DWA算法路径规划图
Fig.8 Conventional DWA algorithm path planning diagrams
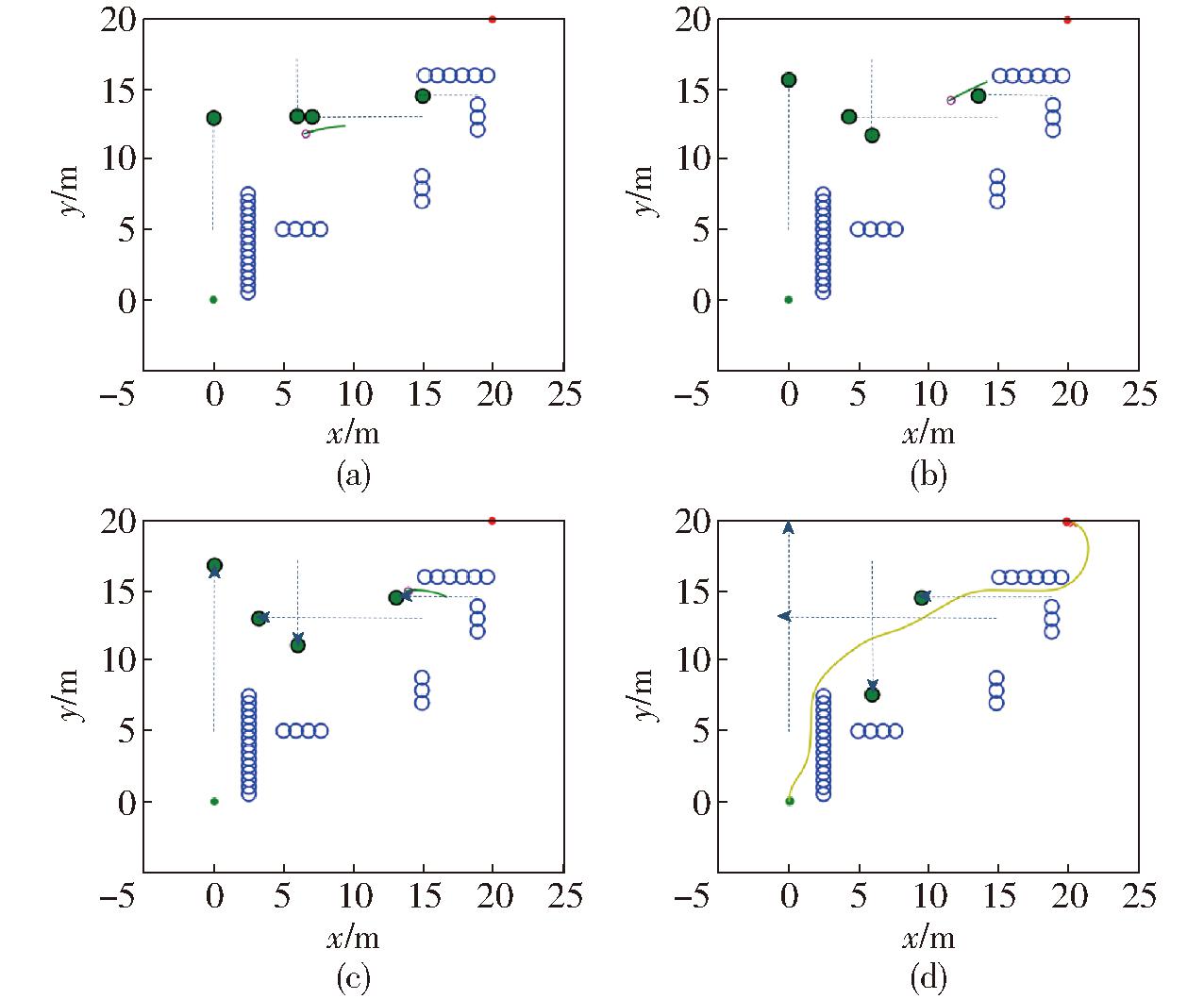
图9 文献[11]算法路径规划图
Fig.9 Path planning diagrams of algorithm of literature[11]
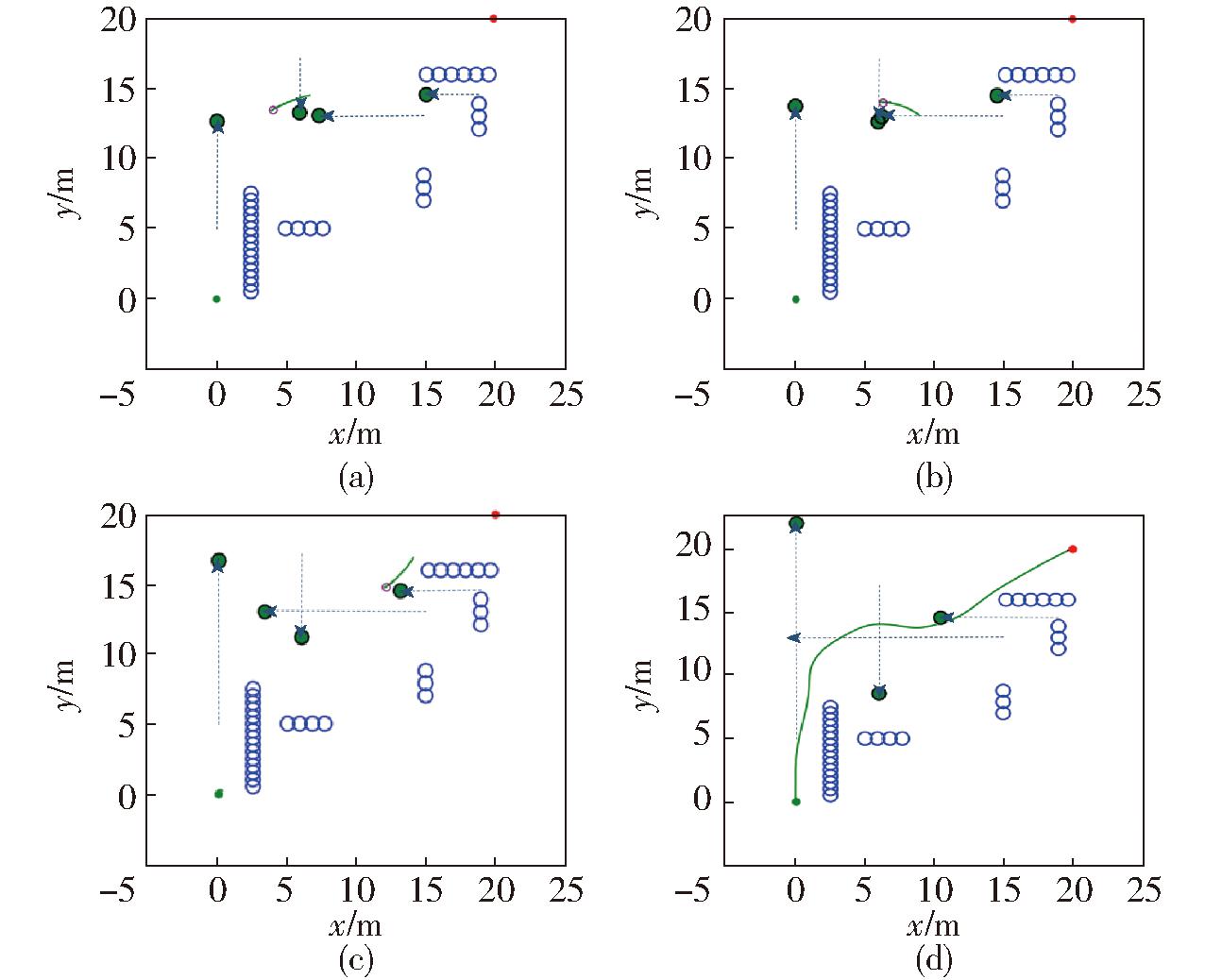
图10 DAV_DWA算法路径规划图
Fig.10 DAV_DWA algorithm path planning diagrams
由图11可知,传统DWA算法权重缺少灵活性,不能较好处理动态障碍物;文献[11]算法在一定程度上避免了碰撞危险,但对于速度和方位角权重变动较大,路径平滑性较差,从而大大延长了路径长度和时间。本文算法对动态障碍物权重系数进行调整,使其既能够很好地躲避动态障碍物,又能保证路径行驶效率,综合性能最佳。
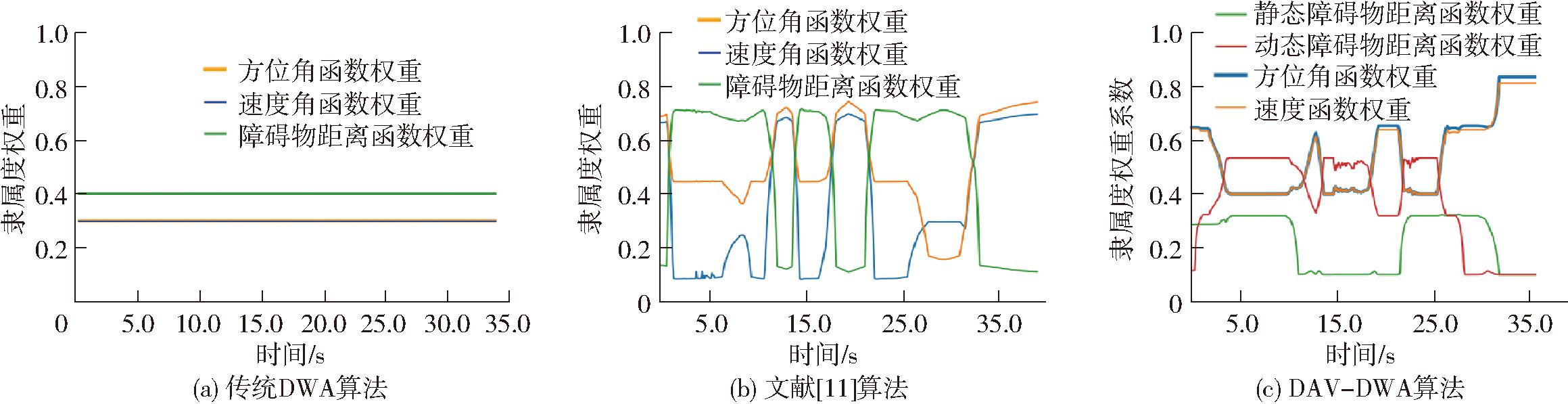
图11 不同算法权重变化曲线(场景2)
Fig.11 Plot of change in weights of different algorithms(Scenario 2)
根据表2及3种算法路径规划图分析,在不与障碍物碰撞的前提下对比,路径长度较文献[11]减少7.6%;寻路时间较文献[11]减少9.0%。传统DWA算法在遇到动态障碍物时不能做到提前采取有效措施避障从而发生碰撞,大大提高了危险程度;文献[11]算法在遇到动态障碍物时,从上方绕行后并未能选择最短路径,与动态障碍物最小距离为0.52 m,这同样对行驶安全构成了潜在威胁。而DAV_DWA算法在与动态障碍物的距离小于预设的特定阈值时即开始避障,从而很好地保持了安全距离,灵活避开动态障碍物且找到了最短路径,在保证安全的前提下,也以最短路径和最少时间到达目的地。
综上所述,DAV_DWA算法相较于传统DWA算法及文献[11]算法,更为充分地考虑了动态障碍物潜在威胁,并通过提前减速,在确保安全平稳到达目标点的前提下,也显著优化了路径规划的效率,从而在动态环境中的路径规划问题上提供了一种更为优越的解决方案。
3.3 场景3(模拟C型障碍物存在空间)
在以下坐标处添加障碍物,形成C型障碍物区域,对传统动态窗口法算法局限性进行分析,具体仿真结果如图12所示。
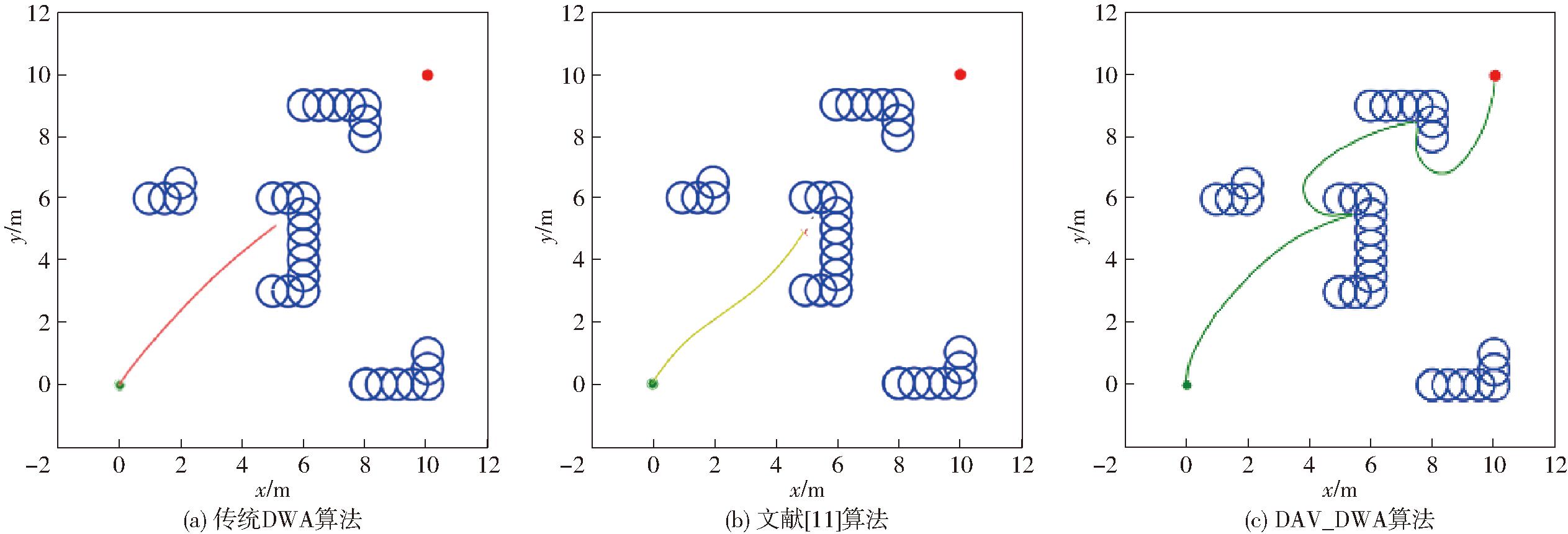
图12 路径规划图
Fig.12 Path planning diagrams
图12a和图12b表明,传统DWA算法和文献[11]算法中机器人在陷入局部最小值后便无法移动,不能自行脱离困境。而由图12c可知,本文算法在机器人到达第1个局部最小值点后设立虚拟目标点,当车辆离开障碍物区后,进一步增设虚拟障碍以免再次陷入此局部最小值点,到达虚拟点后恢复目标点并最终到达,较好地解决了C型障碍物区域无法通过的问题。
4 真实环境下实时路径规划
4.1 试验平台与试验设计
为验证本文算法的可靠性和实用性,于南京丰硕农场高架草莓温室中的转弯通道(宽4 m)进行导航试验。试验机器为长0.8 m、宽0.6 m的履带式机器人,主要由履带底盘、嵌入式工控机、D435i型相机和草莓采摘机构组成,机器人如图13所示。

图13 机器人实物图
Fig.13 Robot physical drawing
1.草莓采摘机构 2.Intel RealSense D435i型相机 3.履带底盘 4.工控机
算法实施方法如下:在导航系统中导入全局地图,通过深度相机检测静态、动态障碍物距离,转换为世界坐标系,添加到全局地图中进行DAV_DWA局部路径规划,获得运动轨迹,机器人通过自适应蒙特卡洛法获得实时位置,且按照最优轨迹对应的线速度与角速度进行运动控制[25]。
进行2种机器人在转弯通道处导航的试验设计:①环境1为温室动静态障碍物并存的环境。②环境2为行人与静态障碍物构成C型障碍物位置的环境。深度相机检测到的动、静态障碍物点均以数字方式标注在图上。
4.2 试验结果与分析
图14a为在温室转弯通道拍摄的机器人在复杂障碍物分布下导航的现场,图14b为路径轨迹图。且如图15所示,机器人在接近动态障碍物时,均会提前减速,平稳通过。温室场景1参数设置及结果为:起始位置(0 m,0 m);目标位置(0 m,4.0 m);实际到达终点(-0.1 m ,4.1 m);最大跟踪误差为0.10 m;定位误差为0.11 m;动态障碍物最小距离为0.76 m;静态障碍物最小距离为0.67 m。

图14 试验场景1及路径轨迹图
Fig.14 Experimental scenario Ⅰ and path trajectory map
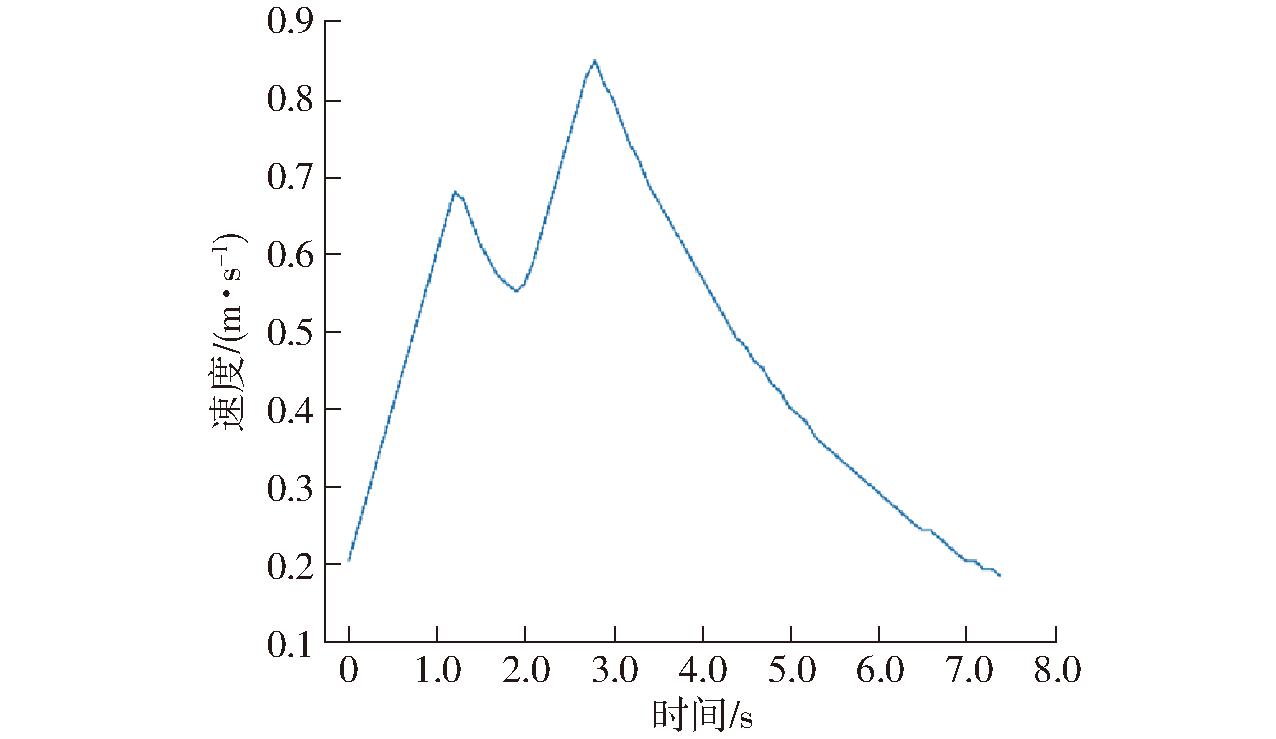
图15 机器人线速度曲线
Fig.15 Robot linear velocity diagram
图16a为在温室转弯通道拍摄的机器人在C型障碍物环境下的导航图像,图16b为路径轨迹图。温室场景2参数设置及结果为:起始位置(0 m,0 m);目标位置(0 m,3.0 m);实际到达终点(0.1 m,3.1 m);最大跟踪误差为0.09 m;定位误差为0.12 m。
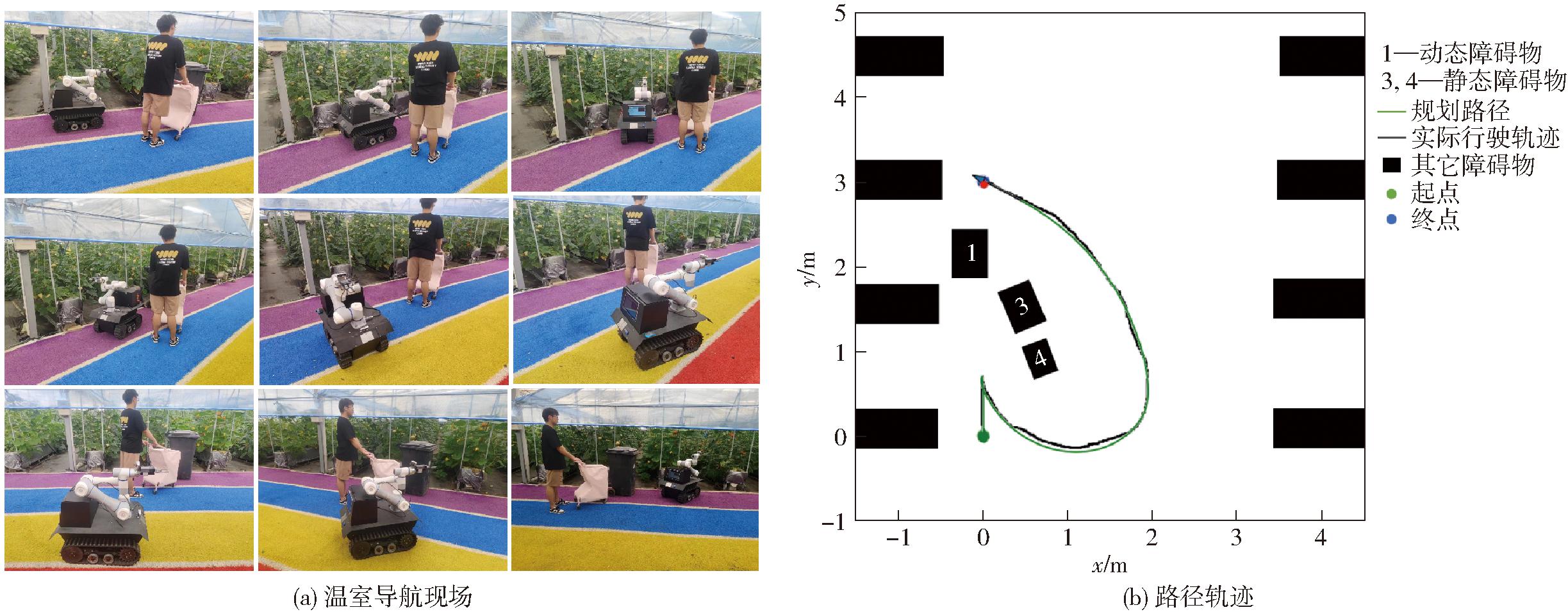
图16 试验场景2及路径轨迹图
Fig.16 Experimental scenario 2 and path trajectory map
试验结果表明,本文算法可以很好地应用于动态障碍物环境,规划的路径能够同时保证安全性和最短路径,且能够很好地应对局部最小值情况。机器人基本可以按照路线达到终点,机器人最终目标点产生的定位误差不大于0.12 m,与规划路径跟踪误差不大于0.10 m,满足实际应用需求。
5 结论
(1)提出了基于双障碍物评价函数、自适应权重和虚拟目标法的动态窗口法(DAV_DWA)。采用了动静双策略的避障方法,降低了动态障碍物碰撞风险且防止过度避障;提出了自适应评价函数权重,引入模糊逻辑算法,根据模糊规则动态输出权重,以增强机器人在不同复杂环境中的路径寻优能力;提出虚拟目标法,增强其陷入局部最小值的脱困能力。
(2)在环境相同的条件下,进行仿真对比试验,仿真结果表明:相较于其他算法,DAV_DWA算法在保证安全性的前提下,到达目标点路径更优,寻路时间更短。
(3)在草莓温室的实际场景中,机器人可以完成自主导航任务,定位误差不大于0.12 m,跟踪误差不大于0.10 m,符合实际需求。
[1] 张美娜,王潇,梁万杰,等.温室远程监控系统人机交互与番茄识别研究[J].农业机械学报,2022,53(10):363-370.
ZHANG Meina,WANG Xiao,LIANG Wanjie,et al.Human-computer interaction and tomato recognition in greenhouse remote monitoring system[J].Transactions of the Chinese Society for Agricultural Machinery,2022, 53(10): 363-370.(in Chinese)
[2] 周俊,何永强.农业机械导航路径规划研究进展[J].农业机械学报,2021,52(9):1-14.
ZHOU Jun,HE Yongqiang.Research progress on navigation path planning for agricultural machinery[J].Transactions of the Chinese Society for Agricultural Machinery,2021,52(9):1-14.(in Chinese)
[3] 荀燕琴.基于群体智能优化的AGV路径规划算法研究[D].长春:吉林大学,2017.
XUN Yanqin.Research on AGV path planning algorithm based on group intelligence optimization[D].Changchun: Jilin University,2017.(in Chinese)
[4] SADIQ A T,RAHEEM F A,ABBAS N A F.Ant colony algorithm improvement for robot arm path planning optimization based on D* strategy[J].International Journal of Mechanical &Mechatronics Engineering,2021,21(1):96-111.
[5] 潘玉恒,奥日格拉,鲁维佳,等.基于动态扩展邻域蚁群算法的移动机器人路径规划[J].农业机械学报,2024,55(2):423-432,449.
PAN Yuheng,Aorigla,LU Weijia,et al.Path planning of mobile robots based on dynamic extended neighborhoods ant colony algorithm[J].Transactions of the Chinese Society for Agricultural Machinery,2024,55(2):423-432,449.(in Chinese)
[6] LIU Weiheng,ZHENG Xin,DENG Zhihong.Dynamic collision avoidance for cooperative fixed-wing UAV swarm based on normalized artificial potential field optimization[J].Journal of Central South University,2021,28(10):3159-3172.
[7] ROESMANN C,FEITEN W,WOESCH T,et al.Trajectory modification considering dynamic constraints of autonomous robots[C]∥Robotics Proceedings of ROBOTIK 2012 7th German Conference on VDE,2012.
[8] FOX D,BURGARD W,THRUN S,et al.The dynamic window approach to collision avoidance[J].IEEE Robotics & Automation Magazine,1997,4(1):23-33.
[9] LI Yue,ZHAO Jianyou,CHEN Zenghua,et al.A robot path planning method based on improved genetic algorithm and improved dynamic window approach[J].Sustainability,2023,15(5):4656.
[10] RICARDO J S,J C P,ALFONSO G.Path planning for autonomous mobile robots:a review[J].Sensors,2021,21(23):7898.
[11] 刘斌,兰莹,黄文焘,等.融合动态窗口法的无人机动态路径规划算法[J].系统仿真学报,2024,36(8):1843-1853.
LIU Bin,LAN Ying,HUANG Wentao,et al.UAV dynamic path planning algorithm combined with dynamic window approach[J].Journal of System Simulation,2024,36(8):1843-1853.(in Chinese)
[12] 赵亮,李春轩,张玮奇,等.基于融合引-斥力与动态窗口法的机器人静动态局部路径规划方法优化[J].信息与控制,2024,53(2):226-237.
ZHAO Liang,LI Chunxuan,ZHANG Weiqi,et al.Optimization of robot static dynamic local path planning method based on integrating attraction-repulsion and dynamic window approach[J].Information and Control,2024,53(2):226-237.(in Chinese)
[13] 王超,梅瑛,张溢,等.基于改进DWA算法的移动机器人避障研究[J].机械设计与研究,2024,40(1):92-96.
WANG Chao,MEI Ying,ZHANG Yi,et al.Research on obstacle avoidance of mobile robot based on improved DWA algorithm[J].Mechanical Design and Research,2024,40(1):92-96.(in Chinese)
[14] 卞永明,季鹏成,周怡和,等.基于改进型DWA的移动机器人避障路径规划[J].中国工程机械学报,2021,19(1):44-49.
BIAN Yongming,JI Pengcheng,ZHOU Yihe,et al.Obstacle avoidance path planning of mobile robot based on improved DWA[J].Chinese Journal of Construction Machinery,2021,19(1):44-49.(in Chinese)
[15] 张星宇,吴保磊,王军,等.基于滑移预测的月球车双层路径规划方法研究[J/OL].系统仿真学报,2024[2024-04-03].https:∥doi.org/10.16182/j.issn1004731x.joss.23-1552.
ZHANG Xingyu,WU Baolei,WANG Jun,et al.Research on dual-layer path planning method for lunar rover based on slip prediction[J/OL].Journal of System Simulation,2024[2024-04-03].https:∥doi.org/10.16182/j.issn1004731x.joss.23-1552.(in Chinese)
[16] 李娟,张子浩,张宏瀚.复杂环境下DWA与RRT算法融合的AUV局部路径规划[J].智能系统学报,2024,19(4):961-973.
LI Juan,ZHANG Zihao,ZHANG Honghan.Local path planning for AUV with fusion of DWA and RRT algorithms in complex environments[J].Journal of Intelligent Systems,2024,19(4):961-973.(in Chinese)
[17] SUN Yicheng,ZHAO Xianliang,YU Yazhou.Research on a random route-planning method based on the fusion of the A* algorithm and dynamic window method[J].Electronics,2022,11(17):2683.
[18] 彭哲,杨兴果.基于改进A*算法的仓库物料车路径规划[J].电工技术,2023(16):20-25.
PENG Zhe,YANG Xingguo.Improved A* algorithm-based path planning for warehouse material trucks[J].Electrical Technology,2023(16):20-25.(in Chinese)
[19] YANG D,SU C,WU H,et al.Construction of novel self-adaptive dynamic window approach combined with fuzzy neural network in complex dynamic environments[J].IEEE Access,2022,10:104375-104383.
[20] 张伟龙,单梁,常路,等.基于改进DWA的多无人水面艇分布式避碰算法[J].控制与决策,2023,38(4):951-962.
ZHANG Weilong,SHAN Liang,CHANG Lu,et al.Distributed collision avoidance algorithm for multiple unmanned surface vessels based on improved DWA[J].Control and Decision Making,2023,38(4):951-962.(in Chinese)
[21] HOSSAIN T,HABIBULLAH H,ISLAM R,et al.Local path planning for autonomous mobile robots by integrating modified dynamic-window approach and improved follow the gap method[J].Journal of Field Robotics,2022,39(4):371-386.
[22] 马金帅,刘兰军,金久才,等.基于改进动态窗口法的无人船目标跟踪运动规划方法[J].海洋技术学报,2022,41(3):1-9.
MA Jinshuai,LIU Lanjun,JIN Jiucai,et al.Motion planning of target tracking for unmanned surface vehicle based on improved dynamic window algorithm[J].Journal of Ocean Technology,2022,41(3):1-9.(in Chinese)
[23] 李明振.室内全向移动机器人路径规划研究[D].南昌:华东交通大学,2022.
LI Mingzhen.Research on path planning of indoor omnidirectional mobile robot[D].Nanchang: East China Jiaotong University, 2022.(in Chinese)
[24] 葛甜,岳佳豪.改进人工势场法的避障轨迹规划[J].汽车实用技术,2023,48(23):50-55.
GE Tian,YUE Jiahao.Improved obstacle avoidance trajectory planning by artificial potential field method[J].Automotive Practical Technology,2023,48(23):50-55.(in Chinese)
[25] 劳彩莲,李鹏,冯宇.基于改进A*与DWA算法融合的温室机器人路径规划[J].农业机械学报,2021,52(1):14-22.
LAO Cailian,LI Peng,FENG Yu.Path planning of greenhouse robot based on fusion of improved A* algorithm and dynamic window approach[J].Transactions of the Chinese Society for Agricultural Machinery,2021,52(1):14-22.(in Chinese)