0 引言
相较于串联机构,并联机构具有刚度和精度高、承载更强、灵活性好等优点[1-2]。随着并联机器人技术不断完善与发展,在农业、航空航天、汽车加工、3D打印等领域被广泛应用[3-6]。其中,Delta并联机器人具有结构简单紧凑、刚度高、速度快等优点[7-8],主要用于钵苗移栽[9-10]、果蔬采摘[11-12]、产品包装与分拣等领域[13-14]。
对Delta机器人而言,通过分析其运动学性能,并进行结构参数优化设计,能使得Delta机器人移速更快,运动过程更平稳。目前,赵杰等[15]运用空间几何学和矢量代数方法建立了运动学正解求解模型,避免了正解多解取舍问题。梁香宁等[16]基于动静平台间的矢量关系,利用数值解法推导出运动学正反解的数值解法。宫赤坤等[17]以雅可比矩阵奇异值和条件数为约束指标,研究操作性能在工作空间内的变化规律。姜轶辉[18]采用数值解法,研究Delta机器人主要结构参数变化对工作空间体积和形状的影响。孔凡国等[19]采用DOE(Design of experiments)选定设计变量,并根据综合灵巧度指标建立结构参数优化模型。高秀兰等[20]以可达工作空间最大内切球体为设计工作空间,利用球体位置及条件数全域平均值进行尺度综合设计。张良安等[21]以雅可比全域均值条件数和全域条件数波动量作为目标函数,提出一种尺度综合方法。胡建平等[22]以可达工作空间与设计工作空间边界距离及条件数约束为目标函数,设计了一款用于钵苗移栽的Delta机器人。李亮等[23]在此基础上引入机构几何尺寸约束为惩罚项,进行了用于分拣的Delta机器人尺度综合设计。臧春田[24]基于运动学分析,给定圆柱体作为设计工作空间,以最大工作空间利用率为目标,建立结构参数优化模型,得到满足要求的最小可达工作空间对应的一组结构参数。
通过上述分析可知,对Delta机器人的尺度综合设计,主要通过建立运动学模型,并基于雅可比矩阵条件数、奇异值、可操作度、可达工作空间等性能指标,构建优化模型求解尺度参数。但针对各结构参数对运动性能的影响分析,及对Delta机器人系统性优化设计依然存在不足。本文在运动学基础上,分析可达工作空间条件数分布特性、各结构参数的约束关系,得出失真约束条件。基于失真约束条件,分析各结构参数变化对运动学性能影响,并基于该影响建立由包络惩罚函数和运动学性能评价函数构成的结构参数优化模型,旨在得到1组使得在可达工作空间内的圆柱体设计工作空间运动学性能最好的结构参数,采用遗传算法得到1组结构参数最优解。取优化前后所得设计工作空间上、中、下3个截面的条件数分布进行对比分析。
1 运动模型建立
1.1 机构简介
如图1a所示,Delta机器人是由上端固定静平台与下端动平台及3条完全相同的支链连接而成的并联机构。其中,每条支链的主动臂通过转动副与静平台连接,2条从动杆通过球副与主动臂、动平台连接,构成平行四边形机构,从而限制整机只有3个移动自由度。根据平行四边形机构特性,可将机构简化为图1b。以静平台外心为坐标系原点O,x轴正向经过点A1,z轴正向竖直向上建立坐标系。令静平台半径lOAi=R,主动臂lAiBi=L1,从动杆lBiCi=L2,动平台半径
主动臂与静平台夹角为θi,3条支链与x轴向支链夹角为αi(0,2π/3,4π/3)。
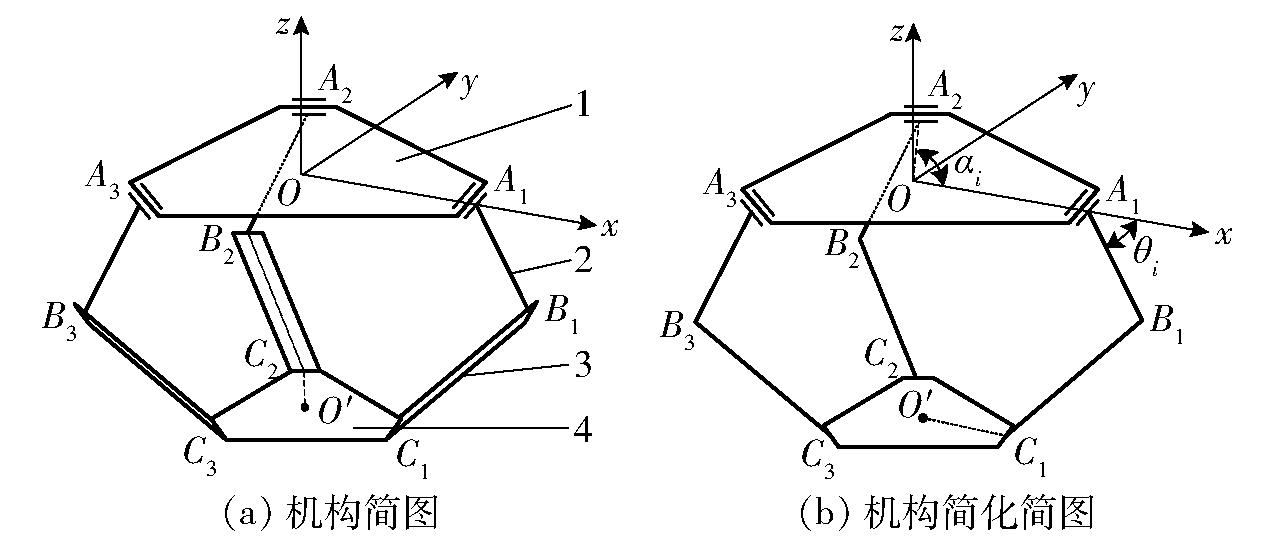
图1 Delta并联机器人结构简图
Fig.1 Delta parallel robot structure schematic
1.静平台 2.主动臂 3.从动杆 4.动平台
1.2 运动学模型
Delta并联机器人运动学分析与尺度综合是以运动学模型为基础。设动平台中心点O′坐标为(xO′,yO′,zO′),在坐标系中点Bi与点Ci位置可表示为
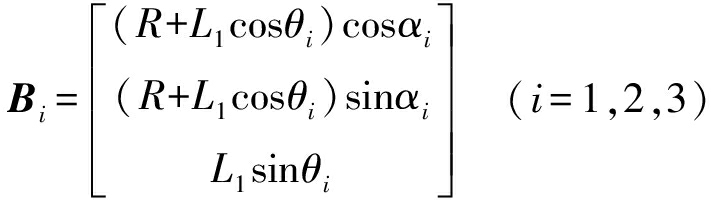
(1)
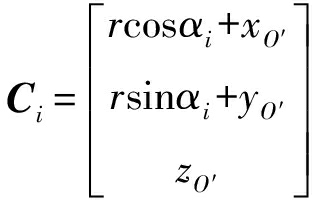
(2)
由
可得
(3)
其中
则有
(4)
(5)
(6)
式(4)～(6)联立得
(7)
其中
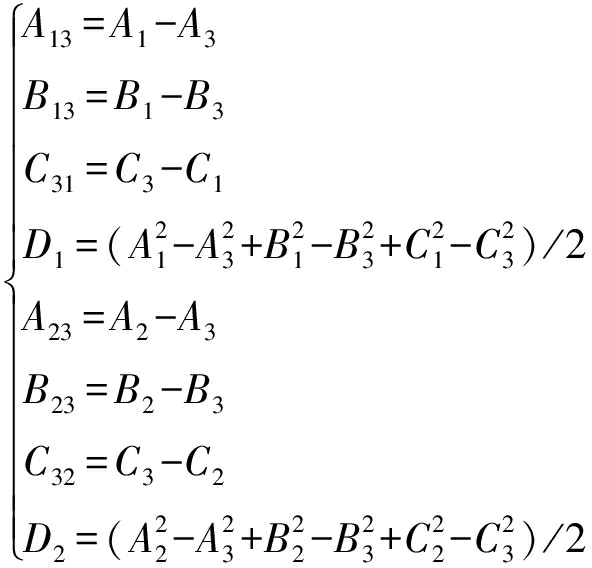
求解式(7)得
(8)
其中
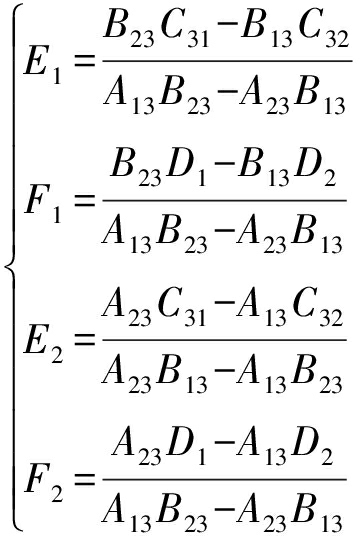
式(8)代入式(6)得
其中
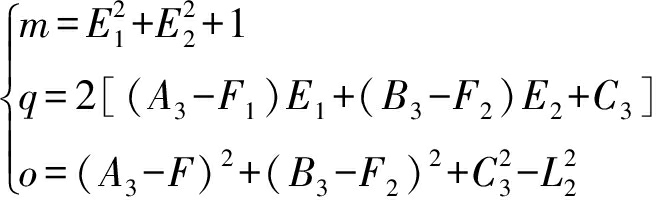
最终得到
(9)
由此可知1组主动臂转角θi作为输入的前提下,可通过式(8)、(9)求得1组点O′坐标。
1.3 雅可比矩阵建立
雅可比矩阵可以反映驱动关节速度与末端执行器运动速度的映射关系[25]。雅可比矩阵求解如下:
式(3)对时间进行微分得
(10)
其中
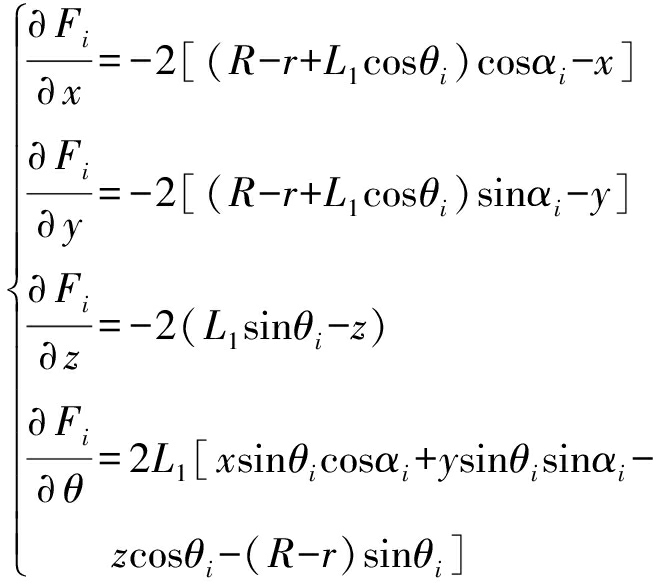
整理得到
(11)
式(11)可改写为
可得雅可比矩阵J为
J=-B-1A
1.4 可达工作空间求解
为保证设计工作空间Wt(圆柱体)被可达工作空间W完整包络,则所有点必须满足3条运动支链构成的边界方程条件。其求解如下:
将式(3)改写为关于θi的方程,即
kicosθi+misinθi+ni=0
(12)
其中
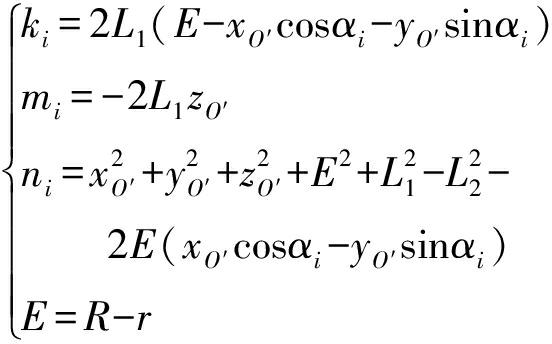
式中 E——动静平台半径差,mm
当且仅当
方程(12)有解,从而得到
(13)
Delta机器人可达工作空间体积可由式(13)求解得出,其结果记为V。当设计工作空间所有点满足Gi(xO′,yO′,zO′)<0时,Wt在W内;当Gi(xO′,yO′,zO′)=0时,为3条运动支链约束下的工作空间边界方程。
以θi∈[-50°,50°]、R=300 mm、r=60 mm、L1=300 mm、L2=800 mm为例生成可达工作空间W,见图2。由图2可知,可达工作空间整体是绕z轴呈120°对称分布的纺锤体结构,上表面3处凹陷绕z轴呈120°对称分布,同时上表面凸起的3条边界对应机器人3条支链。定义Delta机器人在z轴上可达到的上顶点与下顶点分别为上极限点、下极限点。
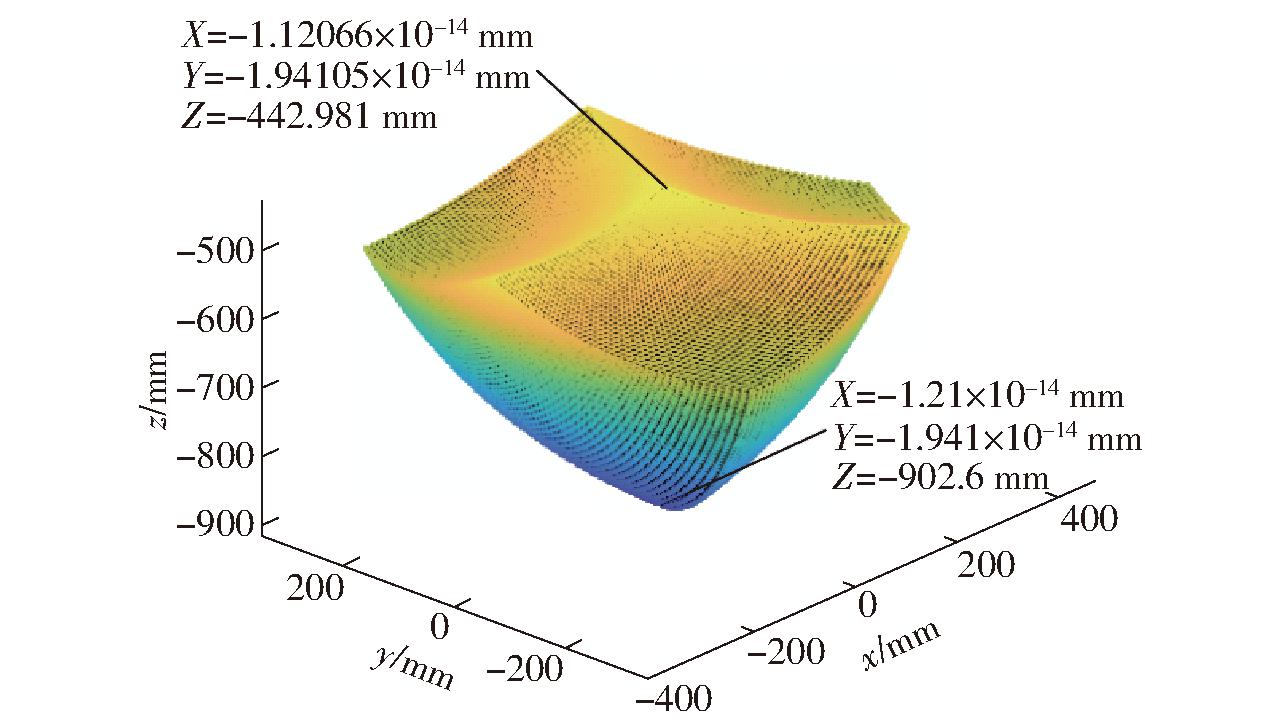
图2 可达工作空间W
Fig.2 Accessible workspace W
本文的设计工作空间Wt(圆柱体)在可达工作空间内,如图3所示,圆柱体为设计工作空间Wt,初始给定Wt的半径r1和高h。
图3 设计工作空间Wt示意图
Fig.3 Schematic of design workspace Wt
2 运动学性能分析
2.1 运动学性能指标
根据1.3节所求的雅可比矩阵,可得雅可比矩阵条件数κ,其通常被用于衡量机器人运动学性能[25],计算式为
(14)
式中 λmax——矩阵JTJ最大特征值
λmin——矩阵JTJ最小特征值
当κ越趋近于1时,表示机构运动学性能越好。
考虑到W内的每个点都有对应的条件数κ,而本文研究对象是全局可达工作空间,故引入κ在W中的全局条件数均值
和全局条件数标准差
作为全局运动学性能指标。计算式为
(15)
(16)
式中 κ(j)——可达工作空间内每个点的条件数
当全局条件数均值趋于1,全局条件数标准差趋于0时,表示机构运动学性能越好。
2.2 可达工作空间条件数分布
以1.4节生成的可达工作空间为例,在上极限点和下极限点之间,以Δz=50 mm做切片处理,每片厚度为3 mm,得到6个截面上的条件数分布情况,如图4所示。以Δz=3 mm连续切割W,得到各截面条件数均值、标准差随z轴变化,如图5所示。
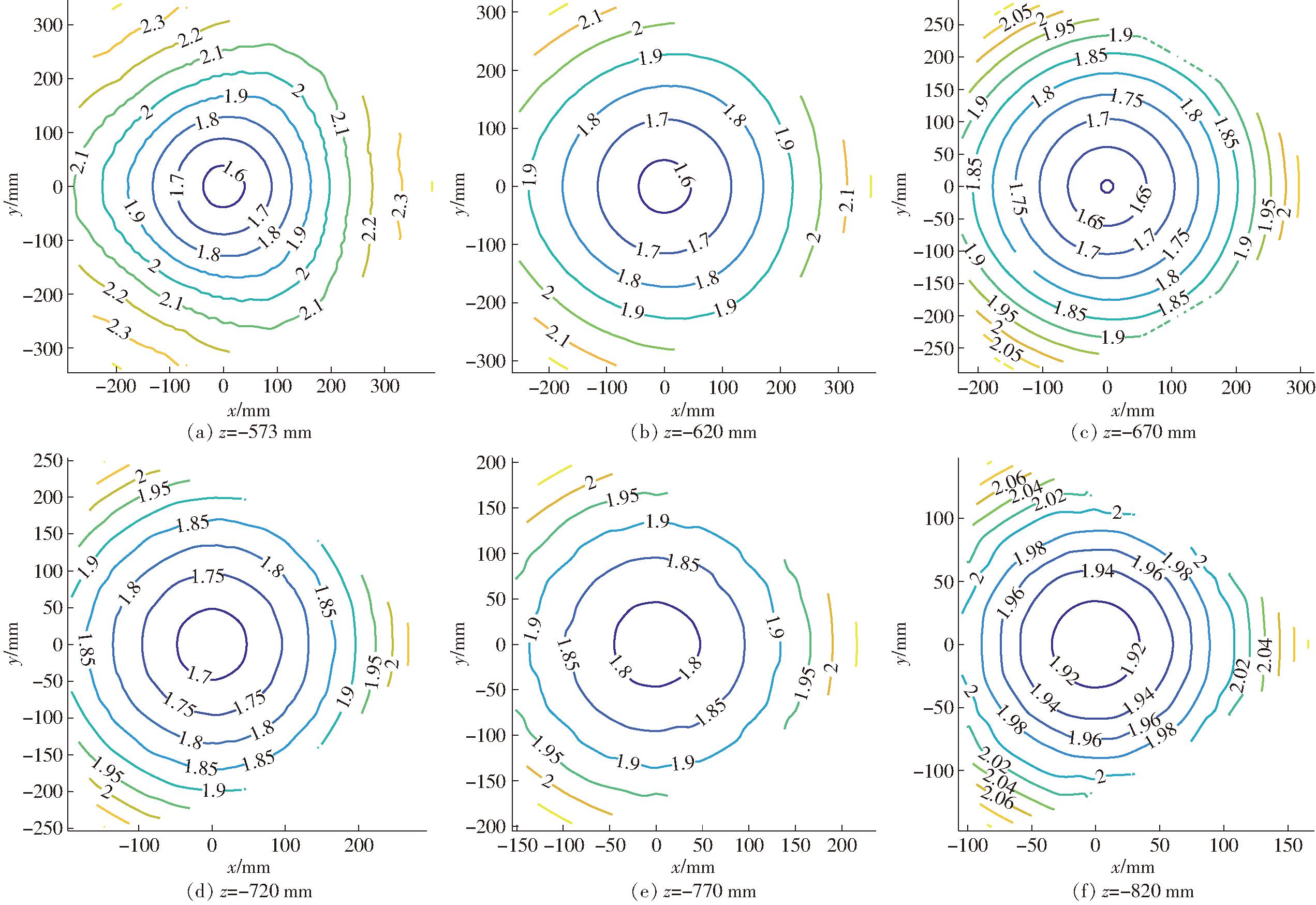
图4 各截面条件数分布规律
Fig.4 Distribution rule of condition number of each section
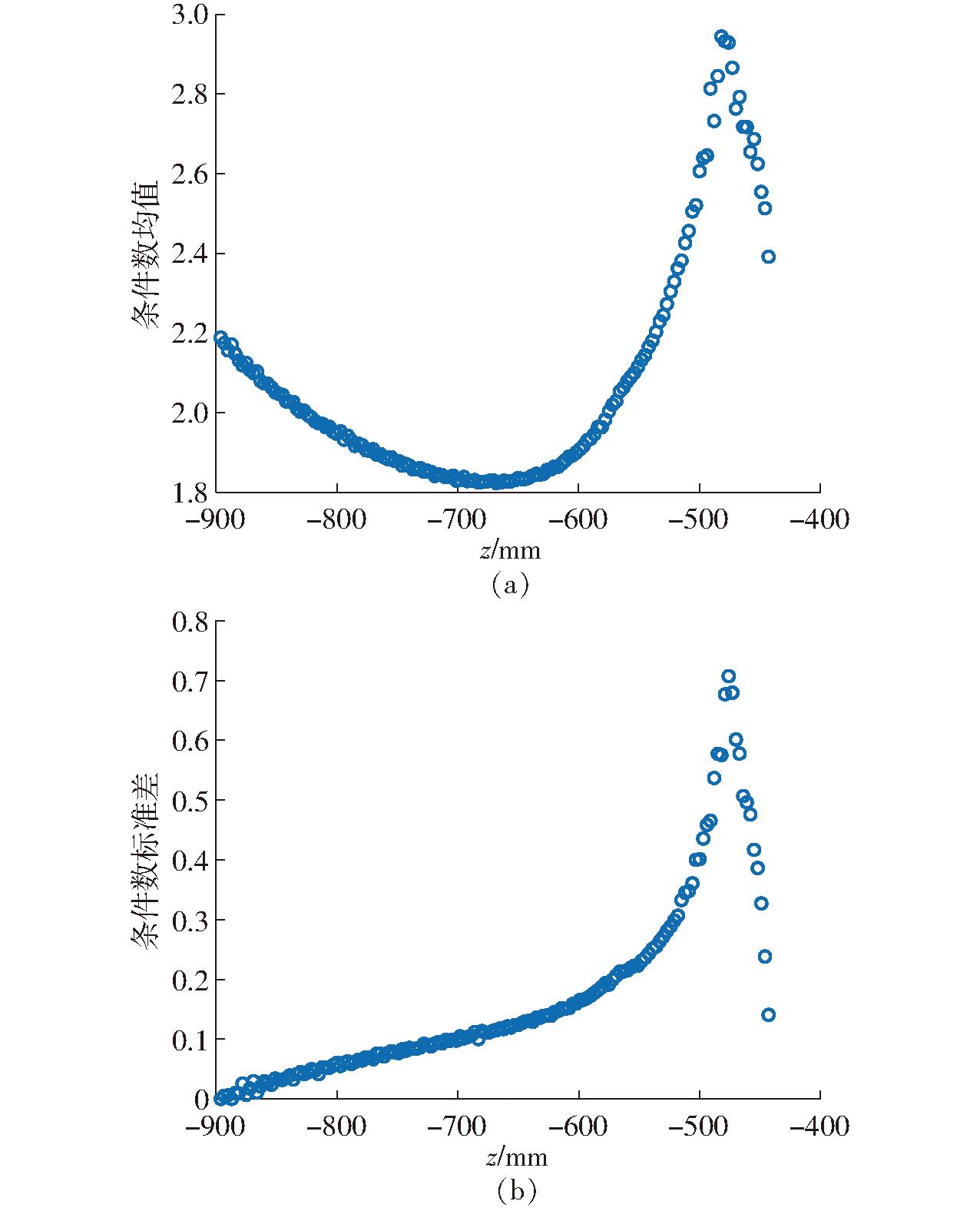
图5 各截面条件数
Fig.5 Number of conditions of each section
分析所得可达工作空间的条件数分布与变化特性如下:①κ分布关于z轴呈120°旋转对称,在z轴上条件数最接近1。②κ沿截面径向增大,且沿z轴负方向,核心区域κ增大,边界κ减小。③沿z轴负方向,各截面均值条件数先减小后增大,呈对称分布。④沿z轴负方向,各切片条件数标准差呈下降趋势,且在z=-600 mm节点之后,下降趋势减缓。
根据条件数对称分布特性,设计工作空间(圆柱体)Wt上表面圆心的(x,y,z)坐标应为(0,0,H),只需确定圆心到静平台中心点垂直距离H,就能确定Wt在W中的位置。
2.3 全局条件数标准差失真
由文献[26]可知,Delta机器人机构存在E<L2-L1约束,但在研究过程中存在一个现象:当取定L1、L2时,虽E在此约束下取值,但E的取值靠近从主杆长差值(L2-L1)时,所得全局条件数标准差会出现失真情况(失真是以条件数标准差有明显突变作为评判标准,如从1突然变为10)。当E逐渐增大时,会导致以下现象:①使机构在运动过程中出现较大的晃动和振动,使运动学和动力学特性变得更为复杂。②由式(12)知,E=R-r,假定R=300 mm, 当E逐渐增大时,势必导致r减小,动平台将趋于一个点,这将导致3条支链对动平台的耦合作用增强。③容易在某些部位产生较大的应力集中。④在运动过程中,因不协调性可能导致更多的能量消耗。
因此当E逐渐增加到某一临界值时,在上述现象的累积影响下,造成Delta机器人运动学性能崩溃,这体现在全局条件数均值和标准差突变。
当L1=300 mm,L2=600 mm,则按几何约束取E<300 mm,当E=204 mm时,突变为41.601 1,在这之后呈无序变化,如图6a所示,这将导致E在(204 mm, 300 mm]中的任意取值与定值L1、L2组成的结构,其可达工作空间内整体条件数与1相差很远,将导致可达工作空间内各点运动学性能变差;而E=192 mm时,由1.589 99突变为4.339 3,且之后呈无序变化,如图6b所示,将导致E在(192 mm,300 mm]中的任意取值与定值L1、L2组成的结构,其可达工作空间内各点间条件数波动变化太大,运动不平稳,会产生较大振动。
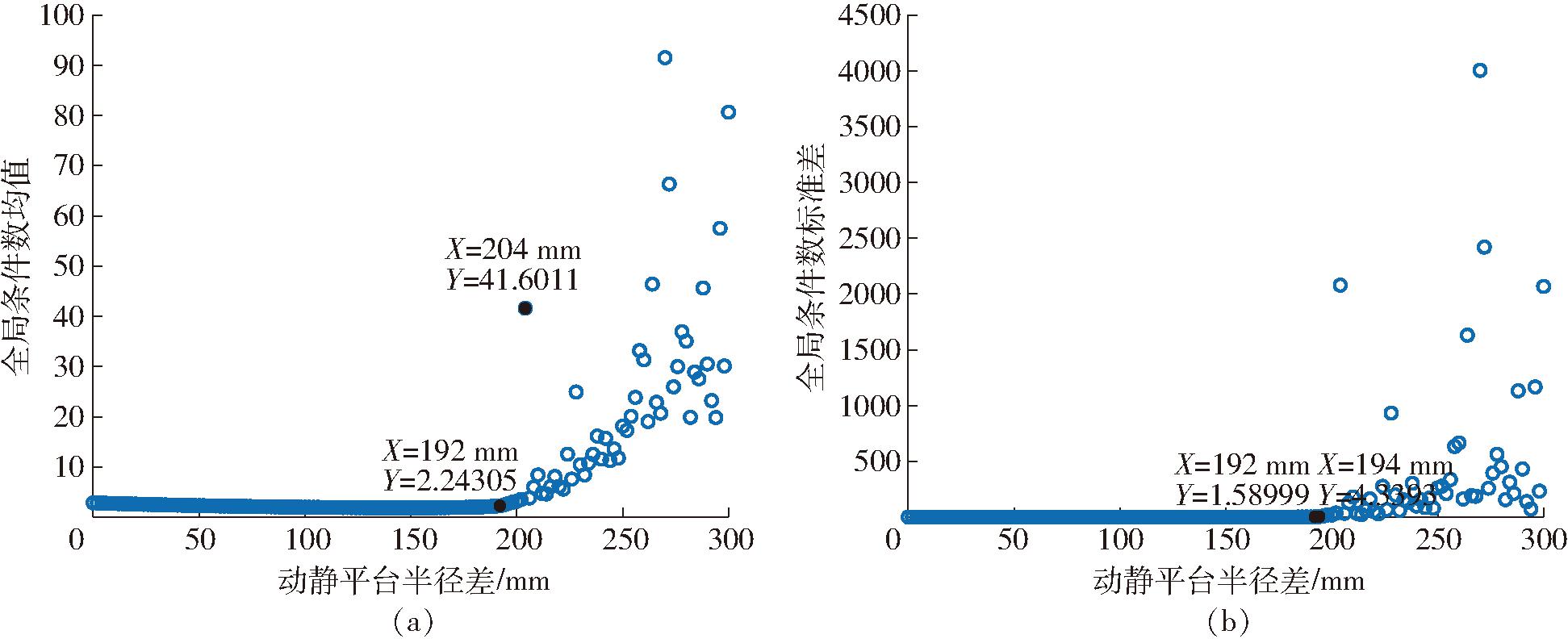
图6 全局条件数失真情况
Fig.6 Distortion of global condition number
综合考虑,只有E在(0 mm, 192 mm]中的任意取值与定值L1、L2组成的结构,其全局条件数均值与标准差视为正常值,其可达工作空间内各向运动学性能符合正常情况,其组成的Delta机器人结构被视为合理。因此,当L1=300 mm、L2=600 mm时,失真节点E1=192 mm。
由图6b可知,针对在E∈(0 mm, 300 mm]时,结合几何学约束E<L2-L1,取不同L1、L2研究失真节点E1随主从杆长差值的变化规律,表1为不同主从杆杆长差值对应的失真节点E1。
表1 主从杆长对标准差失真节点的影响
Tab.1 Influence of master and slave bar length on standard deviation distortion node mm
差值L1L2E1差值L1L2E1300300600192390210600248310300610198400200610256320300620204410200620260330300630210420200630266340300640218430200640272350300650224440200650278360240600230450200660284370230600236460200670290380220600242470200610298
根据表1所得主从杆杆长差值及对应的
失真节点E1的值,得到最小二乘法拟合曲线如图7所示。
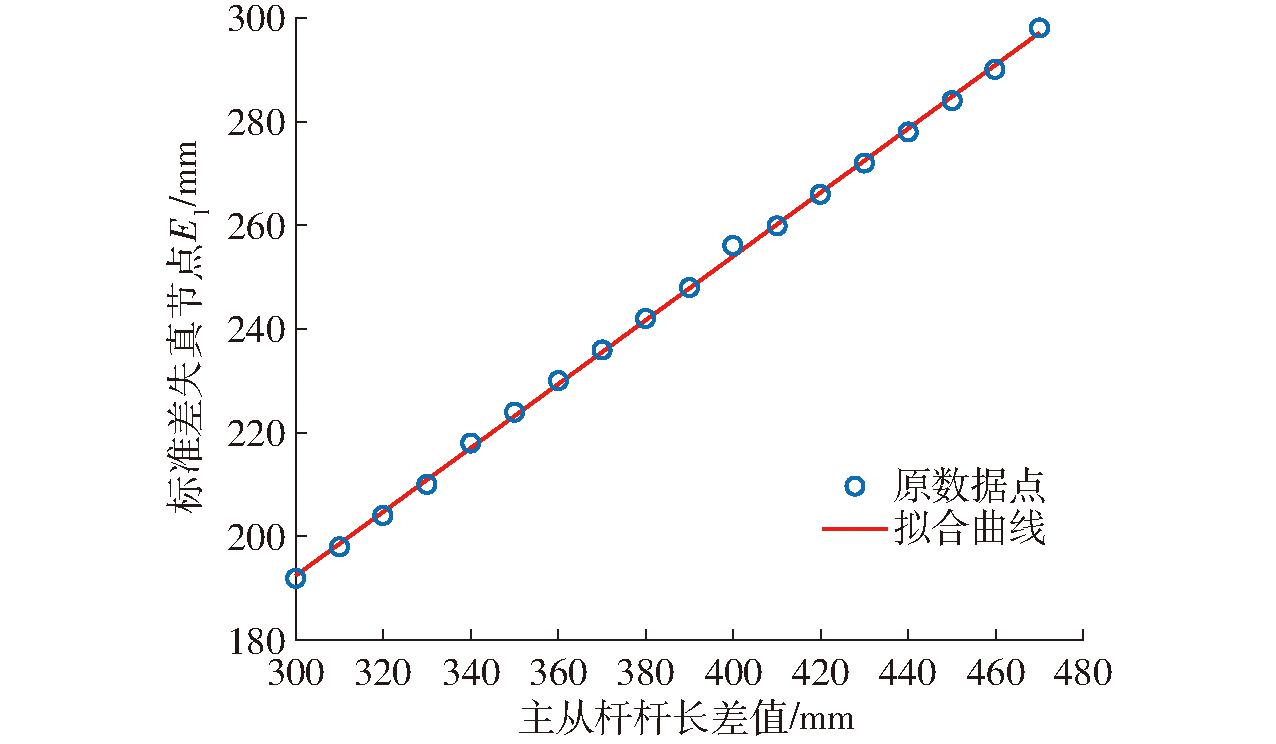
图7 杆长差值与失真节点拟合曲线
Fig.7 Rod length difference and distortion node fit curve
从而得到两者之间的关系函数为
E1=0.615 7(L2-L1)+7.738 6
则主从杆长与动静平台半径差约束为
(17)
2.4 多变量对全局运动学性能的影响
为了分析动静平台半径差E、主动臂杆长L1、从动杆杆长L2对工作空间体积V、全局条件数均值
全局条件数标准差的影响,进行多变量影响分析。假定L1∈[200 mm,500 mm],E分别取160、200、240 mm,则根据2.3节所得的失真约束条件式(17),令E=E1得出,当E=240 mm、L1=500 mm时,可取L2最小值为877 mm,可确定L2∈[900 mm,1 200 mm]。图8为
随E、L1、L2的变化曲面。
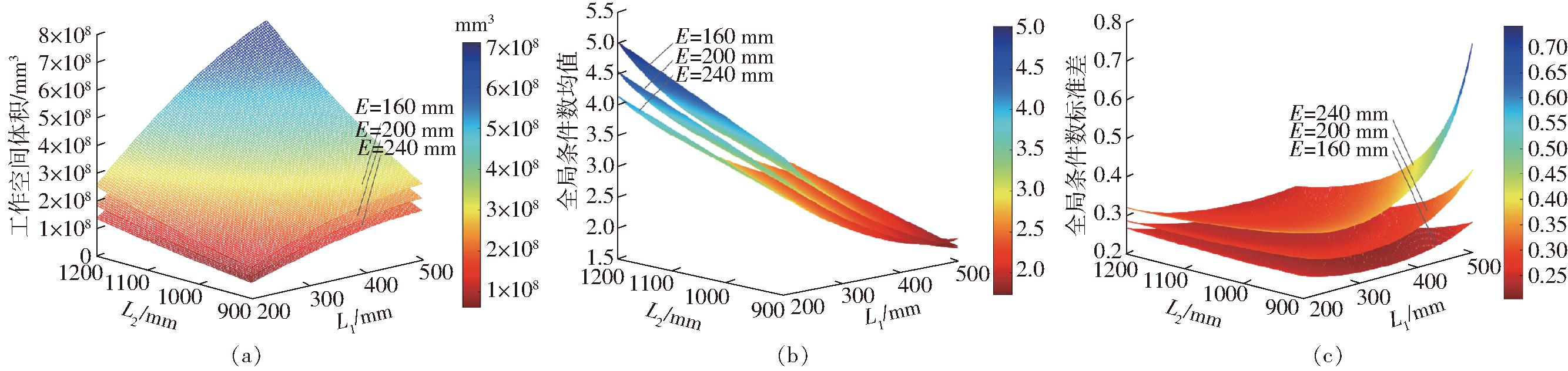
图8 多变量对全局运动学性能的影响
Fig.8 Influence of multiple variables on global kinematic performance
由图8可知,V分别随L1、L2增大而单调增大,随E增大而减小;分别随E、L1增大而单调减小,随L2增大而增大;随L2增加而减小,随L1增大先略有减小后增大,随E增大而单调增大。V在L1和L2最小、E最大时可取得极小值,在E和L1最大、L2最小时可取得极小值。而在L1较大、L2较小时,受E的影响较大,随E减小大幅减小。
上述分析表明,E、L1越大,L2越小,越趋近于1,机器人各向运动学性能越好;在L1较大、L2较小时,受E的影响较大,E越小越趋于0,可达工作空间内各点之间条件数波动越小,其运动学性能越好。
为保证所得设计工作空间内运动学性能较好,应以全局条件数均值最小为第一位,辅以全局条件数标准差一个可以接受的较小范围,在此前提下力求可达工作空间体积最小以保证机器人整体尺寸较小,从而构建结构参数优化模型。
2.5 多变量与全局运动学性能相关性
根据2.4节随E、L1、L2的变化规律所得数据,采用偏相关分析方法,分别分析E、L1、L2与的相关性,得到相关系数,并利用Origin 2021b做出相关性热力图,如图9所示。图中*表示p<0.001,**表示p>0.5,p<0.001时,变量相关性由随机误差产生的概率极低,当p>0.5时,变量相关性由随机误差产生的概率极高。
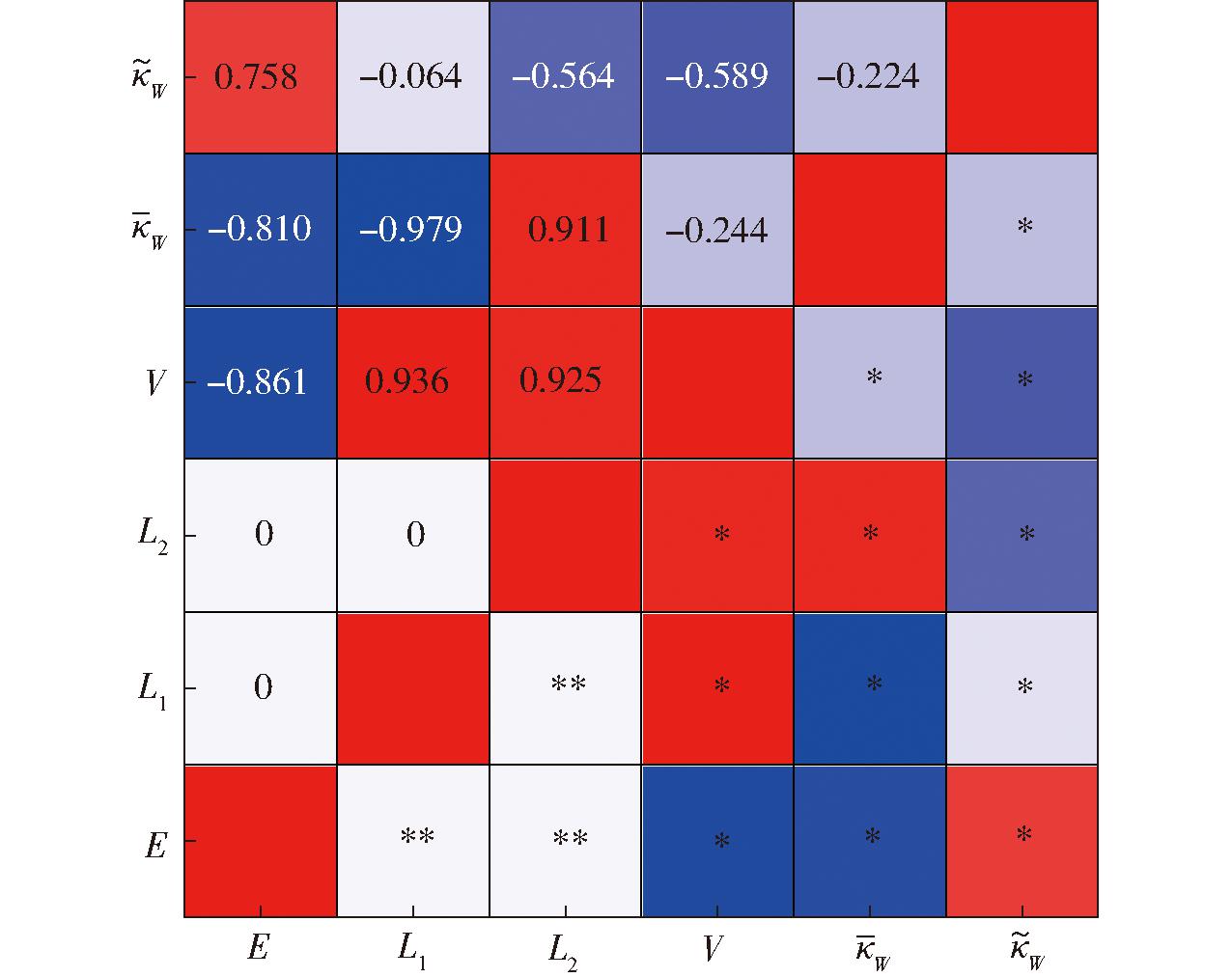
图9 多变量与全局运动学性能的相关性分析
Fig.9 Correlation analysis of multi-variables on global kinematic performance
由图9可知,E、L1、L2由失真约束条件式(17)给出,故三者之间相关系数为0,且显著性p>0.5,相关性不显著;而由E、L1、L2分别计算得出,三者之间为低度相关;E、L2分别与呈高度相关和极高相关,L1与
呈极高相关而与呈极低相关。L1与相关系数仅有0.064,在建立E、L1、L2与的函数关系时可忽略。
3 结构参数尺度综合与优化设计
3.1 结构参数优化设计目标
本文结构参数优化设计是给定一个圆柱体设计工作空间Wt,利用运动学正解模型及第2节中各结构参数对运动学性能进行分析,构建结构参数优化模型,最终得到1组使Wt内运动学性能较好的结构参数。而优化结果应满足基本条件:此圆柱体被W包络。且该组结构参数需实现2个优化目标,目标1:使圆柱体内各向运动学性能达到最好,即设计工作空间内全局条件数均值
最接近1,内部全局条件数标准差
尽可能趋于0。目标2:理论上结构参数无限增大,即可使得W无限增大,z轴条件数趋于1的区域将因此增加,Wt内运动学性能将更好。但该方法不符合实际,且增大结构参数使Wt运动学性能更好的方法将造成Delta机器人整体结构变大、生产成本增加。故在满足基本条件前提下,参数优化模型应使W体积较小,使得Delta机器人整体尺寸较小。
3.2 目标函数建立
3.2.1 包络惩罚函数建立
为满足设计工作空间被工作空间完全包络这一基本条件,将结合条件数分布规律,构建基于空间点位置的包络惩罚函数。为促使最终的优化参数能够得到一个运动学性能较好的设计工作空间,其在可达工作空间内的位置确定如下:
根据2.2节条件数分布与变化特性①,可确定圆柱体上表面圆心坐标为(0,0,H),其中H为静平台坐标系原点到该圆心的距离。根据2.2节条件数分布与变化特性③可知,在可达工作空间内,各截面条件数均值沿z轴负方向有先减小后增大的变化趋势,且沿条件数均值最小截面呈左右对称。基于这一特性,确定圆柱体中心截面与条件数均值最小截面在z轴方向上重合,此位置可保证在W内,Wt的全域条件数均值最小。最后,由图5a可知,条件数均值最小截面基本位于可达工作空间z轴方向上的中心面,且Delta机器人可达工作空间为上大下小的仿锤体结构,因此仅需满足圆柱体下表面被完全包络,则一定能保证圆柱体整体被可达工作空间包络。如此,圆柱体下表面圆心位置为(0,0,(zmax+zmin-h)/2),下表面圆周上的点用Qk(k=1,2,…,3 601)表示,每个点坐标为Qk(r1cosβ, r1sinβ, (zmax+zmin-h)/2),其中β∈[0°,360°],取步长为0.1°,zmax、zmin为在z轴上Delta能达到的上极限点和下极限点位置的z坐标。根据上述分析,只需保证所有Qk点被W包络,即Gi(Qk)≤0(i=1,2,3)。
建立包络惩罚函数为
(18)
其中
3.2.2 运动学性能评价函数建立
采用工作空间体积V、全局条件数均值全局条件数标准差作为运动学性能评价指标。为简化求解的复杂性,将求解Wt运动学性能最优问题转换为求解W内运动学性能最优。
考虑到
并非由关于E、L1、L2的函数直接求出,为便于后续结构参数优化设计,需在2.5节相关性分析的基础上,针对3个结构参数自变量与3个运动学指标因变量分别开展多元回归分析,以确定各运动学性能指标与各结构参数的函数关系。
首先,结合2.4节3个参数取值范围,给定E∈[160 mm,240 mm],步长为2 mm,L1、L2取值与2.4节相同,可通过运动学正解及雅克比矩阵的计算得到与每组结构参数对应的3个运动学性能指标
将所得数据作为回归分析的样本;其次,取E=240 mm、L1=200 mm、L2=1 200 mm时,得到运动学性能指标随E、L1、L2的分布规律,如图10所示。
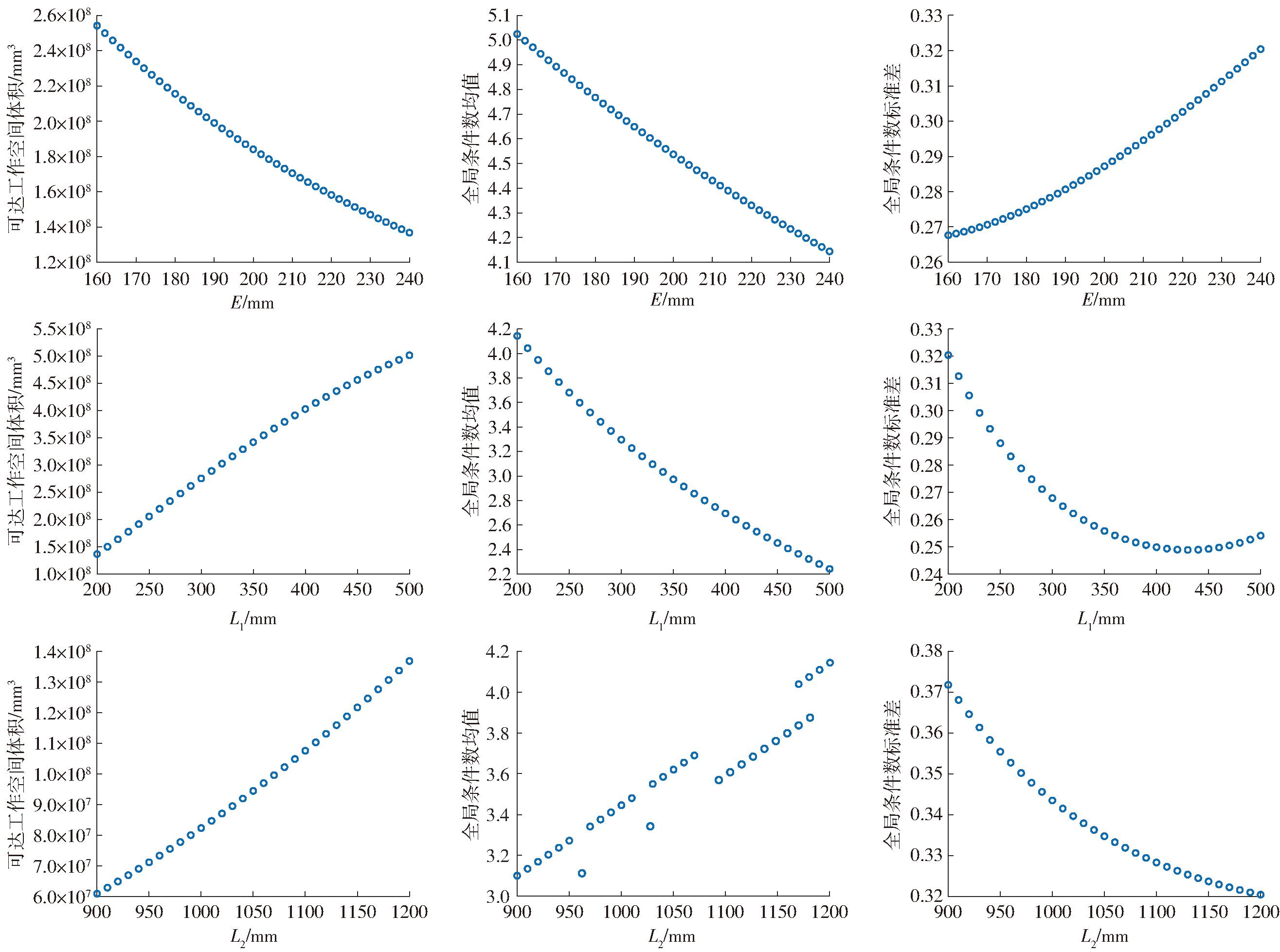
图10 运动学性能分布规律
Fig.10 Distributions of kinematic performance
根据所得数据规律分布图,结合初等函数图像,构建3个关于结构参数的运动学性能指标的多元非线性回归假设模型。由2.5节可知,L1与相关性弱,为降低回归模型复杂程度,考虑将其舍去,对舍去前后作对比分析,舍去L1后,对结果几乎无影响。根据数据分布规律建立的多元非线性回归假设模型为
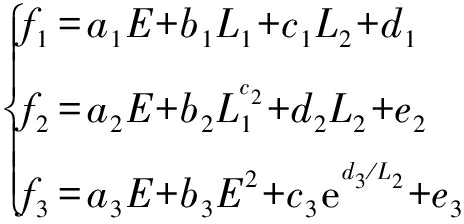
式中 
拟合值
ai～ei——待定参数,i=1,2,3
基于现有样本数据,通过非线性最小二乘法进行参数估计,求解得3个多元非线性回归模型为
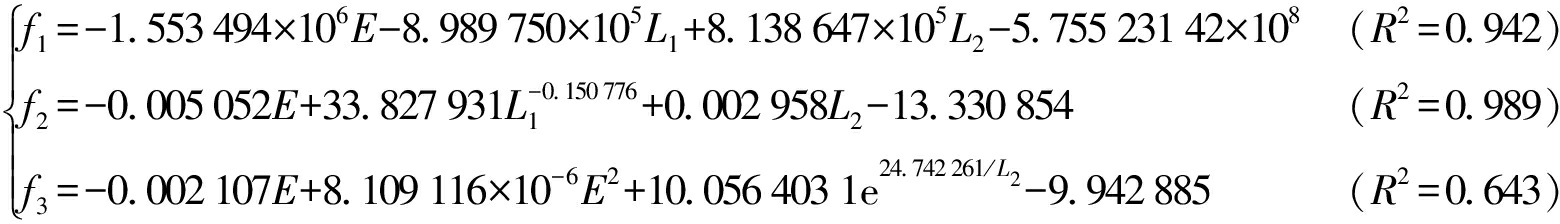
(19)
利用所得运动学性能指标拟合函数求出各指标的拟合值,结果如图11所示,图11a、11b变化规律与图8a、8b基本一致,图11c与图8c极值差距较大,但二者间的变化规律趋于一致,可满足要求。将所得的多元非线性回归模型作为各运动学性能分目标函数。
图11 运动学性能拟合值的变化规律
Fig.11 Influence of multiple variables on global kinematic performance
在3.2.1节Wt在W中的位置分析中,圆柱体中心截面z轴位置被确定于W的中心面所处位置,可保证在满足Wt被W完全包络的各个可达工作空间中,当Wt位于W内此区域时,Wt的全局条件数均值
最接近1。因此,为得到各向运动学性能最优圆柱体设计工作空间,将该问题转换为求解运动学性能最优的可达工作空间。
根据拟合得到运动学性能指标的3个拟合函数,将各指标消除量纲量级,并采用线性加权组合法构建运动学性能评价函数。
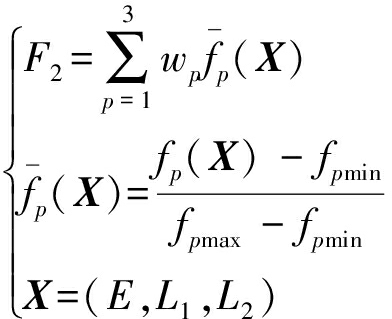
(20)
其中
w1+w2+w3=1
式中 wp——加权因子
fpmin、fpmax——各分目标函数值的最值
3.3 优化模型建立与最优结构参数求解
3.3.1 优化模型建立
根据式(17)主从杆长与动静平台半径差的约束,确定3个结构参数取值范围。采用惩罚函数F1判别在取值范围内的1组结构参数,是否满足Wt被W完全包络这一基本条件。采用评价函数F2中分目标函数
保证所得解构成的设计工作空间内各向运动学性能最优。分目标函数
保证W较小,使得Delta机器人整体结构更紧凑。
为了实现最终所得设计工作空间Wt运动学性能最好(即设计工作空间内全条件数均值最接近1),使得W尽量小这一目标,应优先考虑使
接近最优值,其次要求Wt内各向运动学性能指标波动尽量小(即设计工作空间内全条件数标准差接近0)。基于上述考虑,各分目标函数权重为w1=0.4,w2=0.4,w3=0.2。
由3.2节所得的惩罚函数、评价函数,及主从杆长与动静平台半径差的约束式(17),构建结构参数优化模型为
(21)
3.3.2 模型求解
采用遗传算法[27]对模型求解。遗传算法作为优化搜索算法,被广泛应用于求解各种复杂形式的优化问题。针对本文优化模型,结构尺寸变化范围为:0<L1≤1 500 mm、0<L2≤1 500 mm、0<E≤1 500 mm。 遗传算法各参数设置见表2。
表2 遗传算法参数
Tab.2 Genetic algorithm parameters
参数数值种群个体数N100染色体节点数M3迭代次数T500突变概率Pm0.2交叉概率Pc0.2
图12为结构参数优化流程。在创建初始种群时,判断每个个体是否符合约束条件,符合约束条件的100个个体组成初代种群,这有利于算法快速收敛;计算每个个体适应度,并保存适应度最小的个体;每个个体进行变异处理,产生的新个体满足约束条件则替换原个体,否则保留原个体,染色体交叉处理同理;计算每个个体适应度,当前代适应度最小个体的适应度如果比已保存的适应度最小个体更小则更新适应度最小个体;适应度最小个体将替换适应度高于当前种群整体适应度80%的个体;最后,在迭代500次之后,输出适应度最小个体,即X*(E,L1,L2)。
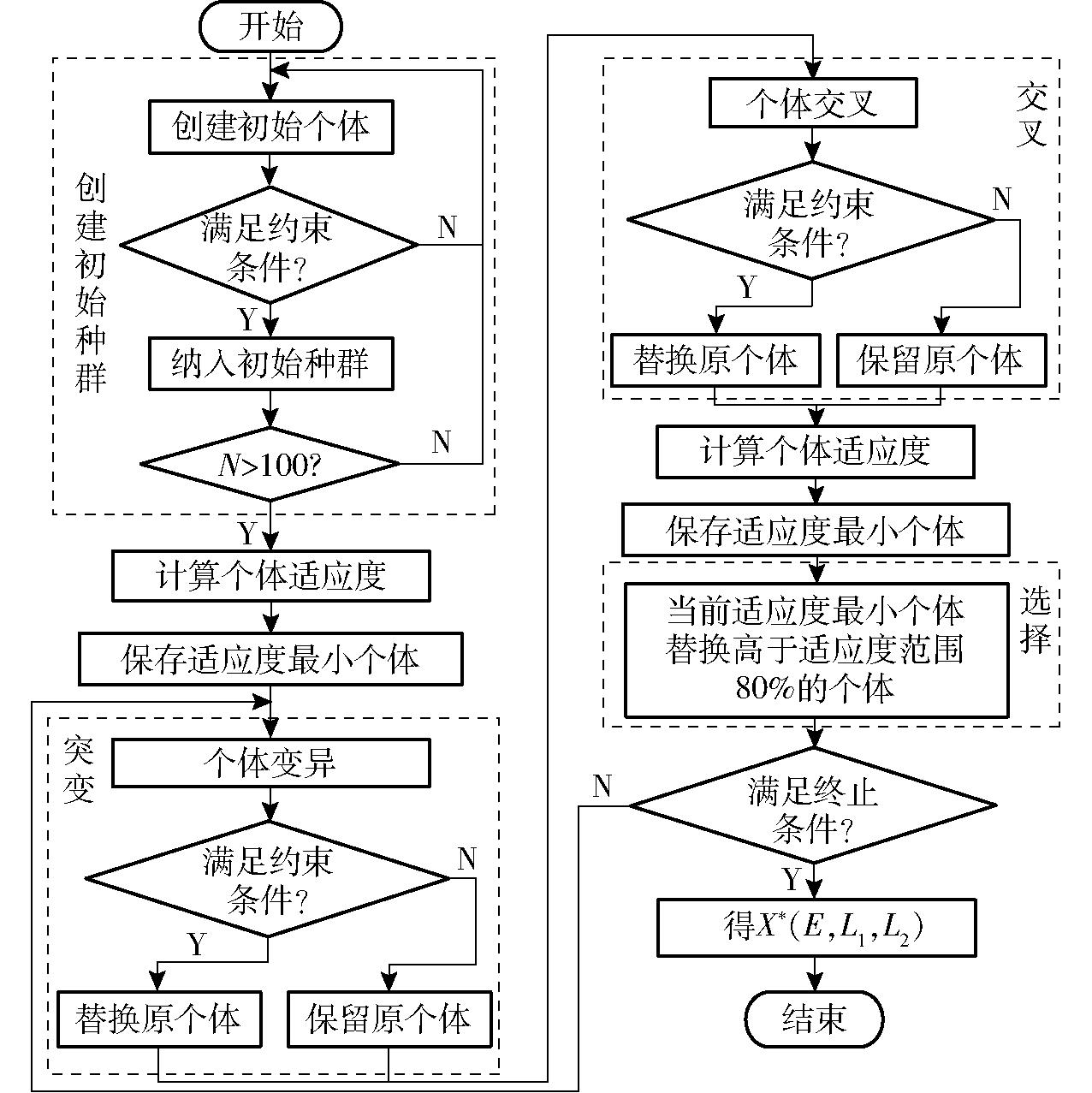
图12 优化流程图
Fig.12 Optimization flowchart
给定设计工作空间r1×h为150 mm×200 mm,主动臂与静平台转角θi∈[-50°,50°]。进行20次求解后,其中8组解如表3所示。与结构参数优化前相比,各组解生成的W体积、Wt内局部条件数均值和标准差优化效果见表4。
表3 优化结果
Tab.3 Optimization result
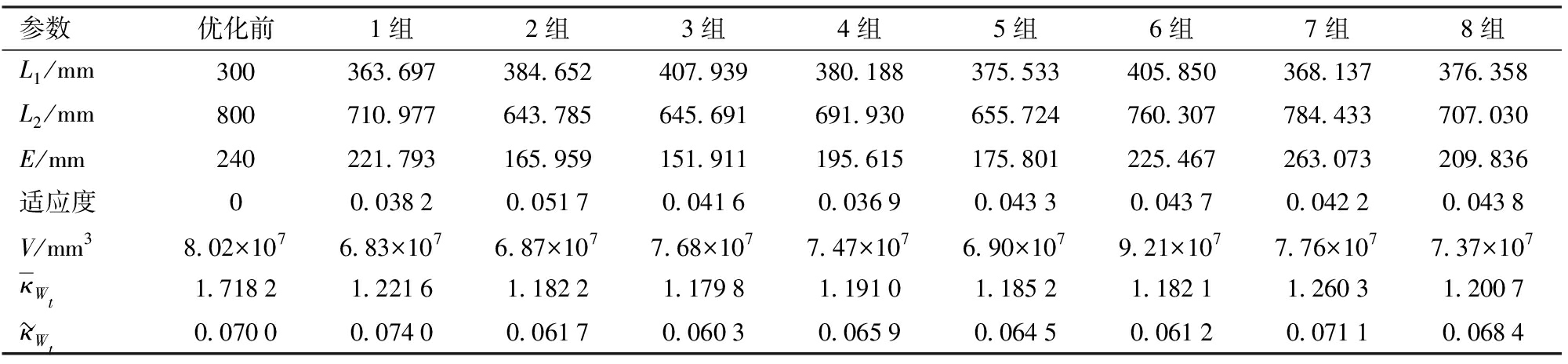
参数优化前1组2组3组4组5组6组7组8组L1/mm300363.697384.652407.939380.188375.533405.850368.137376.358L2/mm800710.977643.785645.691691.930655.724760.307784.433707.030E/mm240221.793165.959151.911195.615175.801225.467263.073209.836适应度00.03820.05170.04160.03690.04330.04370.04220.0438V/mm38.02×1076.83×1076.87×1077.68×1077.47×1076.90×1079.21×1077.76×1077.37×107κWt1.71821.22161.18221.17981.19101.18521.18211.26031.2007κWt0.07000.07400.06170.06030.06590.06450.06120.07110.0684
表4 优化效果
Tab.4 Optimization effect %
参数1组2组3组4组5组6组7组8组V-14.80-14.26-4.20-6.77-13.8914.9-3.19-8.08κWt-28.90-31.20-31.34-30.68-31.02-31.20-26.65-30.12κWt5.74-11.78-13.74-5.76-7.86-12.561.65-2.250
由表4可知,针对
相较于优化前结构参数,8组优化结果减小26.65%～31.34%,其中第2、3、4、5、8组优化结果所得
相比优化前均有减小。第1、6、7组中,二者中某一项在可接受范围内增大,得到另一项有效减小,相比优化前,宏观上呈现性能更好。其中第2组的V减小14.26%的同时,
减小11.78%。故第2组优化效果最好,其优化收敛曲线见图13。第2组解圆整后得到E=168 mm,L1=385 mm,L2=645 mm。Wt上表面与静平台原点的垂直距离H=393.74 mm,故Wt上表面圆心坐标O″(0,0,-393.73 mm)。
图13 优化收敛曲线
Fig.13 Optimal convergence curve
图14a、14b分别表示设计工作空间Wt上、下表面分别与边界方程式(13)所成的3个空间圆环围成的对应可达工作空间截面的位置。由图14可知,第2组结构参数生成的工作空间可完全包络给定的Wt。
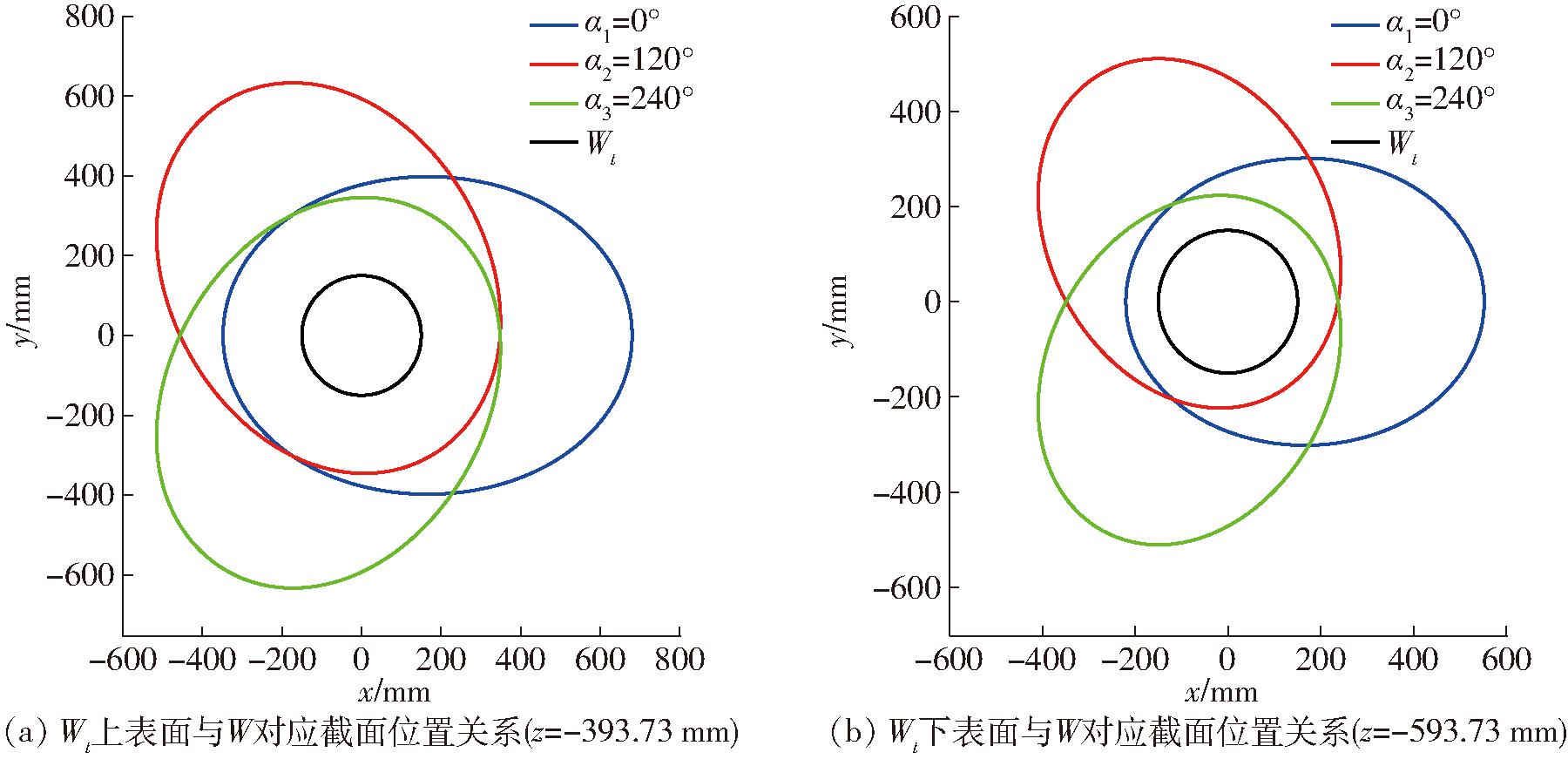
图14 Wt与W位置关系
Fig.14 Position relationship between Wt and W
由优化前和优化后(第2组)的结构参数作Wt上、中、下3个截面条件数分布图,如图15、16所示。并求得各截面条件数均值和标准差,见表5。由表5可知,3个截面条件数均值呈先减小后增大趋势且对称,标准差呈逐渐减小趋势,这与2.2节特性3、4相互验证。另一方面,优化后各截面条件数均值比优化前低,证明优化结果可靠。
表5 各截面条件数均值和标准差
Tab.5 Mean and standard deviation of each section condition number
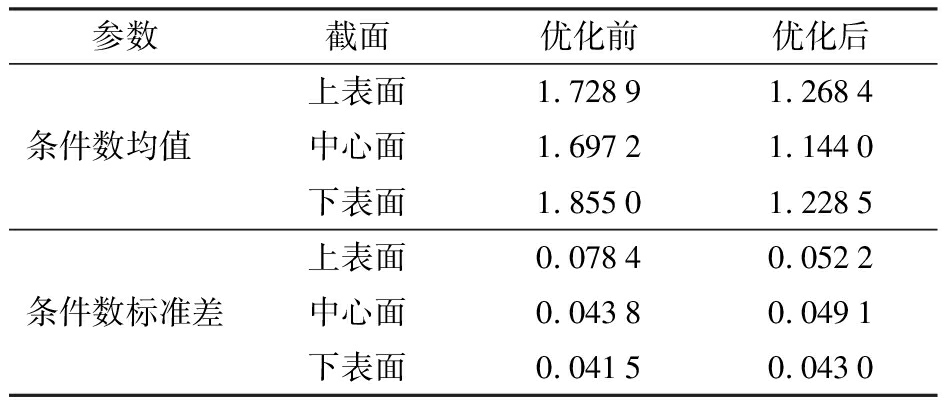
参数截面优化前优化后上表面1.72891.2684条件数均值中心面1.69721.1440下表面1.85501.2285上表面0.07840.0522条件数标准差中心面0.04380.0491下表面0.04150.0430
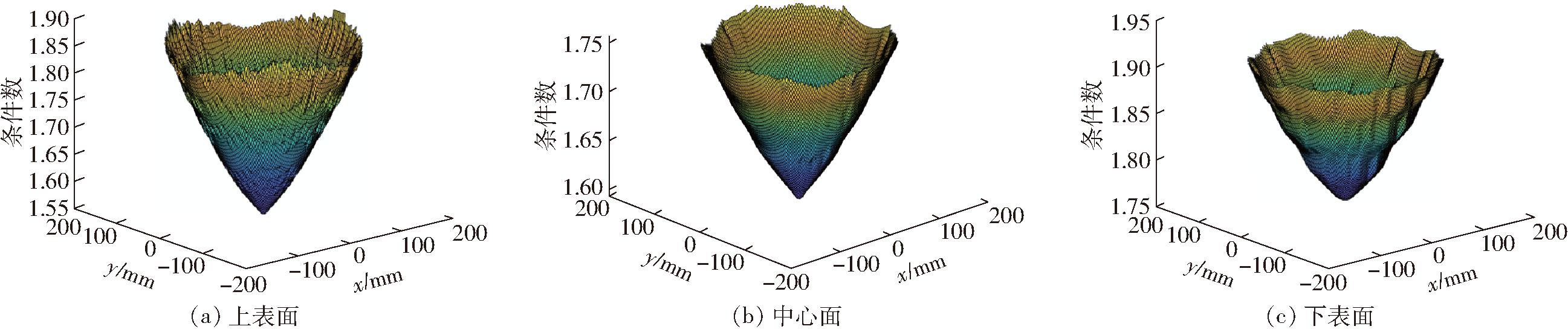
图15 优化前各表面条件数分布
Fig.15 Number distributions of each surface condition before optimization
图16展示优化后的设计工作空间Wt,整体条件数比优化前更接近于1,且截面中心点(即z轴上的点)最接近1,各截面条件数沿径向增大,这与2.2节特性①、特性②形成相互验证。优化后各截面条件数波动情况比优化前更小,且上表面波动减小最大。结合表3与表 4, 相对于其他7组,第2组结构参数所得可达工作空间W体积V相比优化前减小程度最大,从上述分析可得,第2组为这8组优化结果中的最优解。
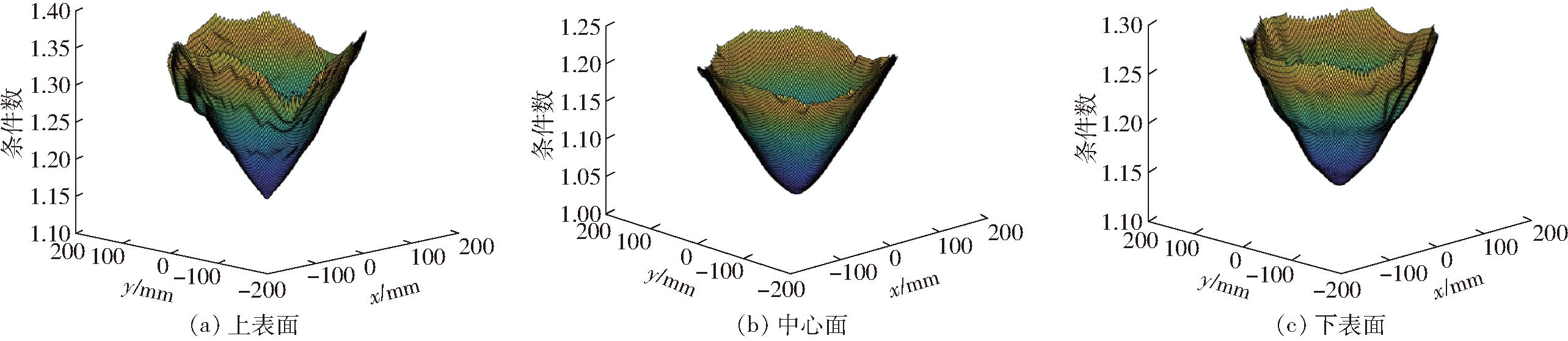
图16 优化后各表面条件数分布
Fig.16 Number distributions of each surface condition after optimization
4 结论
(1)通过分析可达工作空间各截面条件数分布规律得出:当输入转角范围θi∈[-50°,50°]时,各截面条件数分布关于z轴呈120°对称分布且沿截面径向增大,在z轴上最接近1;沿z轴负方向,各截面条件数均值先减小后增大,呈对称分布,条件数标准差呈下降趋势。
(2)通过分析E、L1、L2之间的约束关系,发现不同结构参数所得存在失真现象,并通过多组结构参数分析拟合得到失真约束条件。在此基础上分析E、L1、L2对的影响及相关性分析得出:E与
与
与呈高度负相关;而E与
与V,L2与呈高度正相关;L1与呈低度相关。E、L1越大,L2越小,越趋近于1,机器人各向运动学性能越好;在L1较大、L2较小时,受E的影响较大,E越小越趋于0,可达工作空间内各点之间条件数波动越小,其运动学性能越好。
(3)通过建立包络惩罚函数、运动学性能指标评价函数及失真约束条件,构建优化模型。采用遗传算法进行优化求解,并得到8组较优解。与优化前相比,每组优化结果的减小26.65%～31.34%;对于
每组结果有增有减,但宏观上比优化前更好。其中以第2组(E=168 mm,L1=385 mm,L2=645 mm)优化效果最显著,在V减小14.26%的同时,减小
减小11.78%,因此第2组为8解中的最优解。
[1] 孟庆梅,李佳宇,李菊,等.半对称三平移Delta-CU并联机构运动误差分析与标定[J].农业机械学报,2021,52(1):393-400.
MENG Qingmei, LI Jiayu, LI Ju, et al. Motion error analysis and calibration of semi-symmetric three-translation Delta-CU parallel mechanism[J]. Transactions of the Chinese Society for Agricultural Machinery, 2021, 52(1): 393-400. (in Chinese)
[2] FEDERICO Z, EDOARDO I, SEBASTIEN B. Design and experimental equilibrium stability assessment of a RFRFR continuum parallel robot[J]. Mechatronics, 2023, 95: 103064.
[3] 叶鹏达,尤晶晶,仇鑫,等.并联机器人运动性能的研究现状及发展趋势[J].南京航空航天大学学报,2020,52(3):363-377.
YE Pengda, YOU Jingjing, QIU Xin, et al. Research status and development trend of kinematic performance of parallel robot[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2019, 52(3): 363-377. (in Chinese)
[4] 刘晓飞,刘洋,何阳,等.2RPU+2UPR+RPR多冗余驱动并联机构运动学分析与优化[J].农业机械学报,2023,54(3):440-450.
LIU Xiaofei, LIU Yang, HE Yang, et al. Kinematics analysis and optimization of 2RPU+2UPR+RPR multi-redundant drive parallel mechanism[J]. Transactions of the Chinese Society for Agricultural Machinery, 2023, 54(3): 440-450. (in Chinese)
[5] 李菊,朱忠颀,沈惠平,等.三平移并联机构拓扑设计与运动学分析[J].农业机械学报,2022,53(9):425-433,442.
LI Ju, ZHU Zhongqi, SHEN Huiping, et al. Topological design and kinematic analysis of three-translation parallel mechanism[J]. Transactions of the Chinese Society for Agricultural Machinery, 2022, 53(9): 425-433, 442. (in Chinese)
[6] 周亚杰,李仕华,徐奇,等.3-PUS-PU柔顺并联机构运动学分析与优化设计[J].农业机械学报,2022,53(9):417-424.
ZHOU Yajie, LI Shihua, XU Qi, et al. Kinematics analysis and optimal design of 3-PUS-PU compliant parallel mechanism[J]. Transactions of the Chinese Society for Agricultural Machinery, 2022, 53(9): 417-424. (in Chinese)
[7] WEN K, CHENG Y C, CHANG H H, et al. FPGA-based control design and implementation of Delta robots using horizontal-axial pneumatic actuators[J]. IFAC-PapersOnLine, 2023, 56(2): 11633-11638.
[8] DASTJERDI A H, SHEIKHI M M, MASOULEH M T. A complete analytical solution for the dimensional synthesis of 3-DOF Delta parallel robot for a prescribed workspace[J]. Mechanism and Machine Theory, 2020, 153: 103991.
[9] 高海豹,李瑞琴,宁峰平,等.基于4-CRR并联机构的玉米穴播机运动学分析[J].机械传动,2021,45(12):101-106.
GAO Haibao, LI Ruiqin, NING Fengping, et al. 4-CRR based on parallel mechanism of corn dibbling machine kinematics analysis[J]. Journal of Mechanical Transmission, 2021, 45(12): 101-106. (in Chinese)
[10] 杨启志,孙梦涛,蔡静,等.温室穴盘苗并联高速移栽机器人运动误差分析与试验[J].农业机械学报,2018,49(3):18-27.
YANG Qizhi, SUN Mengtao, CAI Jing, et al. Motion error analysis and experiment of a parallel high-speed transplanting robot for greenhouse cavity disc seedlings[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(3): 18-27. (in Chinese)
[11] 傅雄辉.动态抓取油茶果的Delta机器人轨迹规划研究[D].长沙:中南林业科技大学,2023.
FU Xionghui. Research on trajectory planning of dynamic Delta robot for grasping camellia[D].Changsha: Central South University of Forestry and Technology, 2023. (in Chinese)
[12] 彭艳,刘勇敢,杨扬,等.软体机械手爪在果蔬采摘中的应用研究进展[J].农业工程学报,2018,34(9):11-20.
PENG Yan, LIU Yonggan, YANG Yang, et al. Research progress on application of soft manipulator claw in fruit and vegetable picking[J]. Transactions of the CSAE, 2018, 34(9): 11-20. (in Chinese)
[13] 冯李航,张为公,龚宗洋,等. Delta系列并联机器人研究进展与现状[J]. 机器人,2014,36(3):375-384.
FENG Lihang, ZHANG Weigong, GONG Zongyang, et al. Research progress and status of Delta series parallel robots[J]. Robot, 2014, 36(3): 375-384. (in Chinese)
[14] 张英坤.Delta并联机器人的研究进展[J].机床与液压,2016,44(21):16-20.
ZHANG Yingkun. Research progress of Delta parallel robot[J]. Machine Tool &Hydraulics, 2016, 44(21): 16-20. (in Chinese)
[15] 赵杰,朱延河,蔡鹤皋.Delta型并联机器人运动学正解几何解法[J].哈尔滨工业大学学报,2003,35(1):25-27.
ZHAO Jie, ZHU Yanhe, CAI Hegao. Geometric method for forward kinematics solution of Delta parallel robot[J]. Journal of Harbin Institute of Technology, 2003, 35(1): 25-27. (in Chinese)
[16] 梁香宁,牛志刚.三自由度Delta并联机器人运动学分析及工作空间求解[J].太原理工大学学报,2008,39(1):93-96.
LIANG Xiangning, NIU Zhigang. Kinematics analysis and workspace solution of three-degree-of-freedom Delta parallel robot[J]. Journal of Taiyuan University of Technology, 2008, 39(1): 93-96. (in Chinese)
[17] 宫赤坤,蓝黎恩.基于运动学的Delta机器人优化设计[J].现代制造工程,2013(5):34-37.
GONG Chikun, LAN Lien. Optimization design of Delta robot based on kinematics[J]. Modern Manufacturing Engineering, 2013(5): 34-37. (in Chinese)
[18] 姜轶辉.三自由度Delta并联机器人工作空间研究[D].西安:长安大学,2019.
JIANG Yihui. Research on three-degree-of-freedom Delta parallel robot workspace[D].Xi’an: Chang’an University, 2019. (in Chinese)
[19] 孔凡国,李肇星,柯子旭.Delta并联机器人机构多目标优化设计[J].机床与液压,2022,50(9):35-40.
KONG Fanguo, LI Zhaoxing, KE Zixu. Multi-objective optimization design of Delta parallel robot mechanism[J]. Machine Tool &Hydraulics, 2022, 50(9): 35-40. (in Chinese)
[20] 高秀兰,鲁开讲,王娟平.Delta并联机构工作空间解析及尺度综合[J].农业机械学报,2008,39(5):146-149.
GAO Xiulan, LU Kaiyu, WANG Juanping. Workspace analysis and scale synthesis of Delta parallel mechanism[J]. Transactions of the Chinese Society for Agricultural Machinery, 2008, 39(5): 146-149. (in Chinese)
[21] 张良安,万俊,谭玉良.Ahut-Delta并联机构改进混沌粒子群算法尺度综合[J].农业机械学报,2015,46(8):344-351.
ZHANG Liangan, WAN Jun, TAN Yuliang. Scale synthesis of Ahut-Delta parallel mechanism with improved chaotic particle swarm optimization[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(8): 344-351. (in Chinese)
[22] 胡建平,靳合琦,常燕超,等.基于Delta并联机构钵苗移栽机器人尺度综合与轨迹规划[J].农业机械学报,2017,48(5):28-35.
HU Jianping, JIN Heqi, CHANG Yanchao, et al. Scale synthesis and trajectory planning of pot seedling transplanting robot based on Delta parallel mechanism[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(5): 28-35. (in Chinese)
[23] 李亮,李思凡,王海芳.Delta机器人分拣平台的机构尺度综合与分析[J].中国工程机械学报,2021,19(2):158-163.
LI Liang, LI Sifan, WANG Haifang. Mechanism scale synthesis and analysis of Delta robot sorting platform[J]. Chinese Journal of Construction Machinery, 2021, 19(2): 158-163. (in Chinese)
[24] 臧春田.Delta并联机器人结构设计及优化研究[D].太原:中北大学,2021.
ZANG Chuntian. Structural design and optimization of Delta parallel robot[D]. Taiyuan: North University of China, 2021. (in Chinese)
[25] 宋灵芝.二自由度DELTA并联机器人结构分析及优化[D].太原:中北大学,2021.
SONG Lingzhi. Structure analysis and optimization of two-degree-of-freedom DELTA parallel robot[D].Taiyuan: North University of China, 2021. (in Chinese)
[26] 刘嘉琦.Delta并联机器人工作空间分析及参数优化[D].昆明:昆明理工大学,2024.
LIU Jiaqi. Workspace analysis and parameter optimization of Delta parallel robot[D].Kunming: Kunming University of Science and Technology, 2024. (in Chinese)
[27] 李翠明,任柯州,龚俊.基于改进遗传算法的清洁移动机械臂运动学逆解[J].太阳能学报,2022,43(7):180-185.
LI Cuiming, REN Kezhou, GONG Jun. Inverse kinematics of clean mobile manipulator based on improved genetic algorithm[J]. Acta Energiae Solaris Sinica, 2022, 43(7): 180-185. (in Chinese)
