0 引言
目前国内果园面积达1.23×107 hm2,果品产量和需求量位居世界第一,但现阶段我国果园作业仍以人工为主,果园机器人智能化水平发展相对缓慢[1]。自主导航作为实现果园机器人智能化发展的关键技术,能有效提高机器人作业效率和质量[2-4],减轻果农的劳动强度。
路径规划作为自主导航中的核心技术之一,主要由全局静态路径规划和局部动态避障规划两部分组成[5]。全局静态路径规划是在已知先验环境信息的情况下,寻找一条连接起始点和目标点并避开途中静态障碍物的路径,其主要分为以RRT算法为代表的基于采样搜索的路径规划算法和以A*算法为代表的基于启发式搜索的路径规划算法[6-8]。A*算法利用启发函数在地图中搜索节点,根据各个节点的评价值进行启发式搜索,具有对环境反应迅速、搜索路径直接等特点,但在复杂地图中,随着搜索节点数的增多,节点评价值计算量变大,运算时间变长,搜索效率会大幅降低[9-10]。
针对传统A*算法存在的不足,一些学者提出多种改进方法,杨芳清等[11]提出32邻域A*算法,在传统8邻域基础上采用扩展32邻域搜索策略,提高搜索范围减少路径拐点,但在复杂环境下探索的冗余节点过多,评价值计算量较大,搜索效率大大降低。吴鹏等[12]采用起点终点双向搜索方式结合正反向交替搜索机制,以提高搜索效率,但也存在搜索节点数量以及生成路径中包含的转折点数量较多、路径长度并非最优等问题。李晓露等[13]提出将父节点的选取范围扩展到所有支路节点,舍去冗余的中间路径点,减少路径转折点,降低路径复杂度,但生成路径未经平滑处理,转弯曲率较大。李二超等[14]提出分段和插值贝塞尔曲线优化折线段路径的方式,提高路径平滑度,减小转弯曲率,但随着插值控制点数增加,贝塞尔曲线计算量会变大,对曲线的控制也会减弱。
本文针对传统A*算法规划效率低、规划路径折线段多、折线角度大、作业不稳定等问题,提出一种基于改进A*和LM-BZS算法的路径规划方法。首先,根据先验地图确定不可通行区域并对其进行膨胀处理;其次,引入启发函数权重,根据当前探索进度动态调整节点评价值中实际代价和估计代价的占比,在探索最优路径的同时兼顾搜索效率;为缩小搜索范围并快速避开环境中的障碍物,引入动态5邻域搜索机制,提高路径搜索速度;最后,采用中线投影和LM-BZS算法相结合的方式对规划路径点进行二阶段平滑处理。
1 算法原理
1.1 传统A*算法
传统A*算法是基于搜索邻域和代价函数在已知先验环境信息情况下求解最优路径的搜索算法[15]。通过建立待检查节点列表open_set和已检查节点列表close_set[16],由起始点开始,将起始点Pstart作为当前节点放入open_set列表中,将其节点属性设置为父节点,确定其周围8个方向为子节点邻域并放入open_set中,同时将父节点放入close_set中,通过启发函数H(n)[17]分别计算当前节点n到周围邻域的估计代价值,结合实际代价函数G(n)计算出当前节点n向周围邻域探索的评价函数 F(n)[18],并从中选择具有最小F(n)值的邻域节点作为下一轮探索的父节点,如此往复探索,不断更新,直至找到目标点,通过从目标点回溯每一轮探索的父节点生成最优路径[19]。传统A*算法评价函数F(n)表示为
F(n)=G(n)+H(n)
(1)
启发函数在选取节点到目标点距离时,一般采用曼哈顿距离度量移动代价,计算公式为
H(n)=|x1-x2|+|y1-y2|
(2)
式中 (x1,y1)——当前节点坐标
(x2,y2)——目标点坐标
1.2 路径生成与优化流程
传统A*算法虽能规划出最优路径,但路径拐点较多且距离障碍物较近[20],不符合果园履带机器人的实际作业要求,若要改变航向,需要对其中不符合机器人行驶条件的路径点[21]进行修正,同时为使机器人在改变航向时满足曲率约束条件,需要对规划路径做平滑处理,生成及优化路径流程如图1所示。
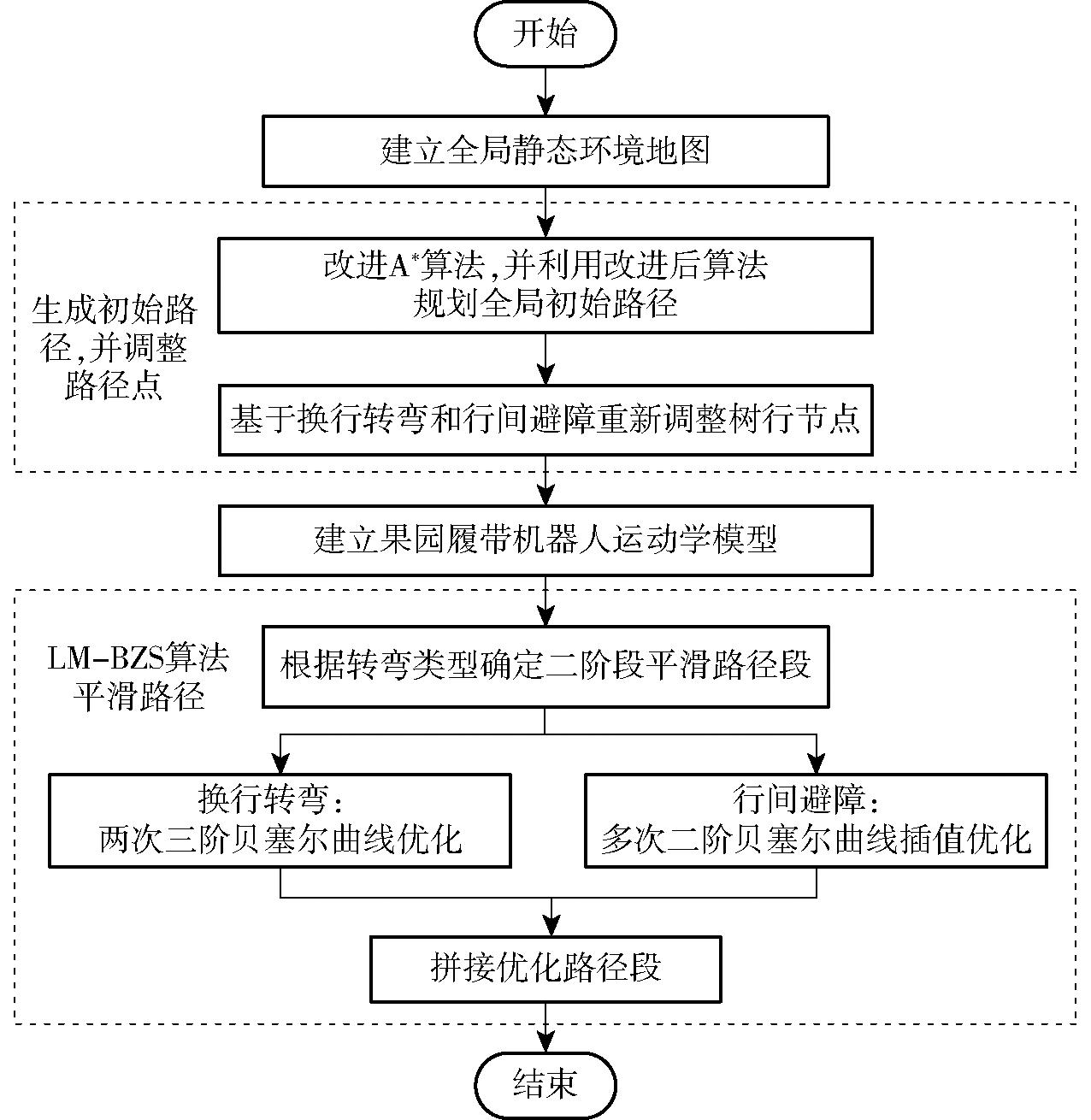
图1 生成及优化路径流程图
Fig.1 Generated and optimized path flow diagrams
2 改进A*算法
2.1 动态选择搜索邻域
传统A*算法将当前节点周围8个方向确定为搜索邻域[22],在果园环境下移动机器人探索路径时会出现很多不必要的探索方向,极大影响搜索效率[23]。本文根据目标点相对于移动机器人当前所在节点计算出位置向量,根据向量坐标确定所属象限,将8邻域搜索改为动态5邻域搜索,减少算法迭代次数和节点代价计算,位置向量表示为
(3)
式中 Vx——目标点相对于当前节点的位置向量
xcurnode——当前节点横坐标
xgoalnode——目标点横坐标
根据向量Vx位置确定搜索邻域,当|Vx|<0时,保留子节点1、5、6、7、8,舍弃子节点2、3、4;当|Vx|>0时,保留子节点1、2、3、4、5,舍弃子节点6、7、8。搜索规则如图2所示。
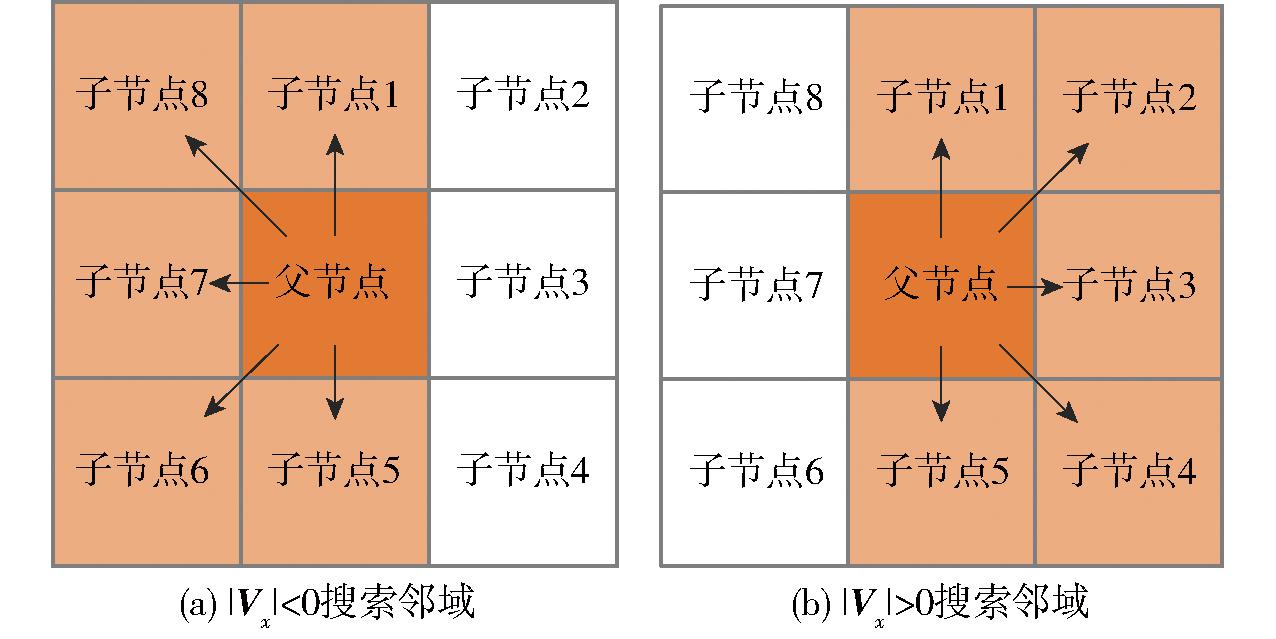
图2 5邻域动态搜索节点图
Fig.2 5 neighborhood dynamic search node graph
2.2 动态设置启发函数
传统A*算法评价函数F(n)由实际代价G(n)和估计代价H(n)两部分组成,H(n)是A*算法中的启发函数,其作用是在规划路径时为算法指明正确的探索方向[24]。与G(n)相比,当H(n)所占比重较大时,此时算法更看重估计代价,计算速度快,但不一定能找到最优路径[25];当G(n)所占比重较大时,虽然能找到最优路径,但搜索范围大,计算速度慢[26]。在极端情况下,当G(n)=0时,此时算法变成基于贪心策略的广度优先算法;当H(n)=0时,算法就退化成Dijkstra算法。因此,可以通过给启发函数添加动态权重以控制A*算法的搜索速度和精确度,在搜索开始时,快速到达目的地所在区域更重要;在搜索到目标点区域时,找到最佳路径更重要。改进后评价函数为
(4)
式中 w(n)——权重函数
R——起始点到目标点距离
r——当前节点到目标点距离
a——权重比例系数
随着搜索区域的深入,当前搜索节点n离目标点越近,距离r越小,权重w(n)越小,则启发函数所占比重相应减小,此时路径规划以探索最优路径为主。
2.3 路径优化
传统A*算法通过启发函数明确搜索方向,探索过程会朝着目标点的方向偏移,所规划路径紧贴树行膨胀区域,导致避障和转弯路径折线段偏多,折线角度偏大,容易在自主作业过程发生碰撞,影响果园机器人自主导航作业效率。因此在规划路径后应基于换行转弯和行间避障行走模式对树行节点进行重新调整,先将路径点分为树行区域路径点和行间路径点,对于树行区域路径点,采用顺序斜率检测方式确定树行中心点和中心两侧点,树行中心点保持横纵坐标不变,而中心两侧点则向相邻侧树行中线平移;对于行间路径点分为行间中线无障碍投影和中线避障投影两种情况进行处理。
2.3.1 树行区域路径点处理
对于树行区域路径点,通过相邻两路径点斜率k1、k2关系可以判断出树行路径点属性,两点式斜率计算公式为
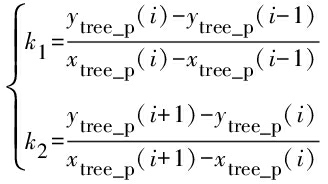
(i=1,2,…,n)
(5)
式中 xtree_p——树行区域路径点横坐标
ytree_p——树行区域路径点纵坐标
根据树行区域相邻两路径点斜率规律,对该区域路径点进行调整,调整方式是树行中心路径点横纵坐标不变,中心两侧相邻路径点分别向邻近树行中线平移,纵坐标则根据转弯方式进行上移或者下移,调整规则如表1所示。
表1 树行路径点调整规则
Tab.1 Tree-row waypoint adjustment rules

斜率关系转弯方式树行点属性横坐标调整方式纵坐标调整方式k1>0;k2=0树行上方转弯树行中心左侧路径点xtree_p(i)=xtree_p(i)-Δxxtree_p(i+1)=xtree_p(i+1)xtree_p(i+2)=xtree_p(i+2)+Δxytree_p(i)=ytree_p(i)+Δyytree_p(i+1)=ytree_p(i+1)+Δyytree_p(i+2)=ytree_p(i+2)+Δyk1=0;k2>0树行下方转弯树行中心右侧路径点xtree_p(i)=xtree_p(i)+Δxxtree_p(i-1)=xtree_p(i-1)xtree_p(i-2)=xtree_p(i-2)-Δxytree_p(i)=ytree_p(i)-Δyytree_p(i-1)=ytree_p(i-1)-Δyytree_p(i-2)=ytree_p(i-2)-Δy
树行区域路径点经过平移调整,折线段长度变短且折线曲率减小,后期经二次规划处理后的路径平滑度会更高,表1中平移距离计算公式为
(6)
式中 Δx、Δy——水平平移距离、竖直平移距离
εx、εy——平移权重
dx——树行中心两侧路径点与邻近树行中线距离
dy——树行路径点与膨胀树行距离
2.3.2 树行中线无障碍投影
树行间路径点进行中线投影时,如果中线相应位置无障碍物约束,直接将树行间路径点投影至树行中线上,树行中线无障碍投影如图3所示,投影处理过程满足
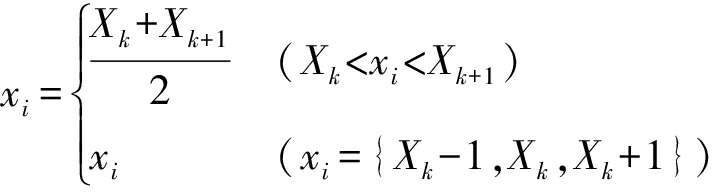
(i=1,2,…,n;k=1,2,…,m)
(7)
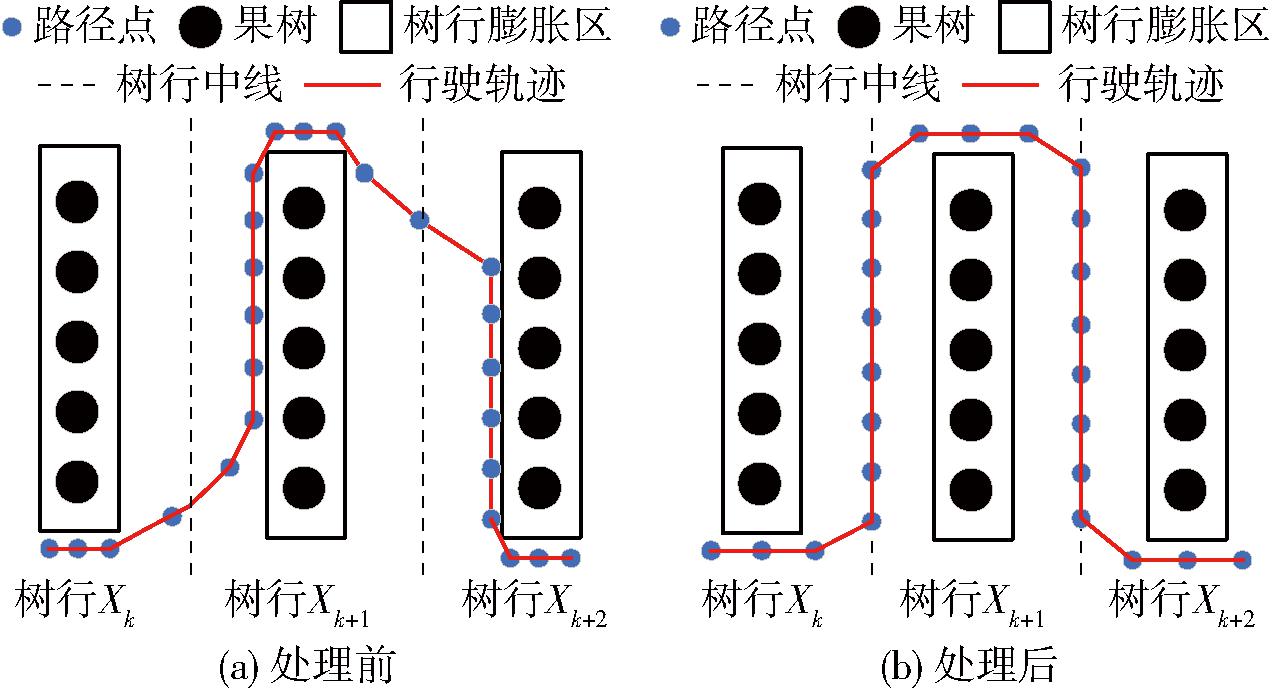
图3 树行中线无障碍投影
Fig.3 Barrier-free projection of midline of tree row
式中 k——树行索引
xi——树行间路径点横坐标
Xk——树行中心横坐标
2.3.3 树行中线避障投影
树行中线投影位置有障碍物时,需要对路径点进行避障投影处理,处理过程如下:探索障碍物左右空间,将路径点向没有障碍物的一侧作投影处理,同时取出障碍物区域前后连续2个相邻路径点向无障碍物一侧依次投影,由于前后2点分别关于障碍物区域对称,以障碍物区域后连续2点为例,避障处理过程满足
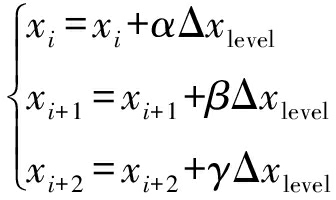
(8)
式中 xi+1——行进方向障碍区域后第1路径点横坐标
xi+2——行进方向障碍区域后第2路径点横坐标
Δxlevel——中线投影点与障碍物边界水平距离
α、β、γ——x轴方向偏移权重
规定障碍物在履带机器人行驶方向左侧越过中线时,偏移权重大于0;障碍物在行驶方向右侧越过中线时,偏移权重小于0,如图4所示。
图4 树行中线避障投影
Fig.4 Obstacle avoidance projection of midline of tree row
通过对规划路径点进行中线投影处理,优化转弯节点位置,减小转弯折线角度,修正路径点的偏移问题,并将路径分为规则直线和曲线段,方便后续利用贝塞尔曲线算法进行平滑处理。
2.4 转弯曲率约束
采用果园履带机器人作为研究对象,其底盘为差速履带底盘,基于左右履带速度变化实现前进和转弯动作。左右履带速度计算公式为
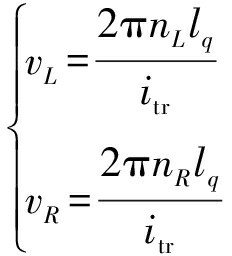
(9)
式中 nL——左侧履带转速
nR——右侧履带转速
vL——左侧履带速度
vR——右侧履带速度
lq——履带驱动轮圆心离地距离
itr——减速器传动比
假设果园履带机器人为刚体结构,在树行间执行作业任务和改变航向情况下运动速度较为缓慢,滑移率和滑转率可以忽略不计,而履带底盘在低速行驶时所受侧向力较小,假设不会发生侧滑现象,其运动学模型如图5所示。若在作业过程中要改变航向,需要满足曲率约束条件
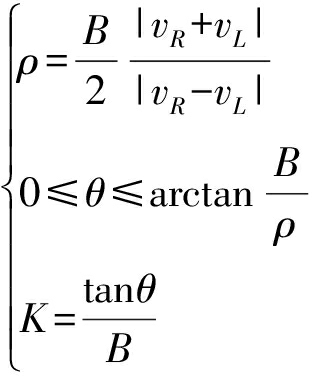
(10)
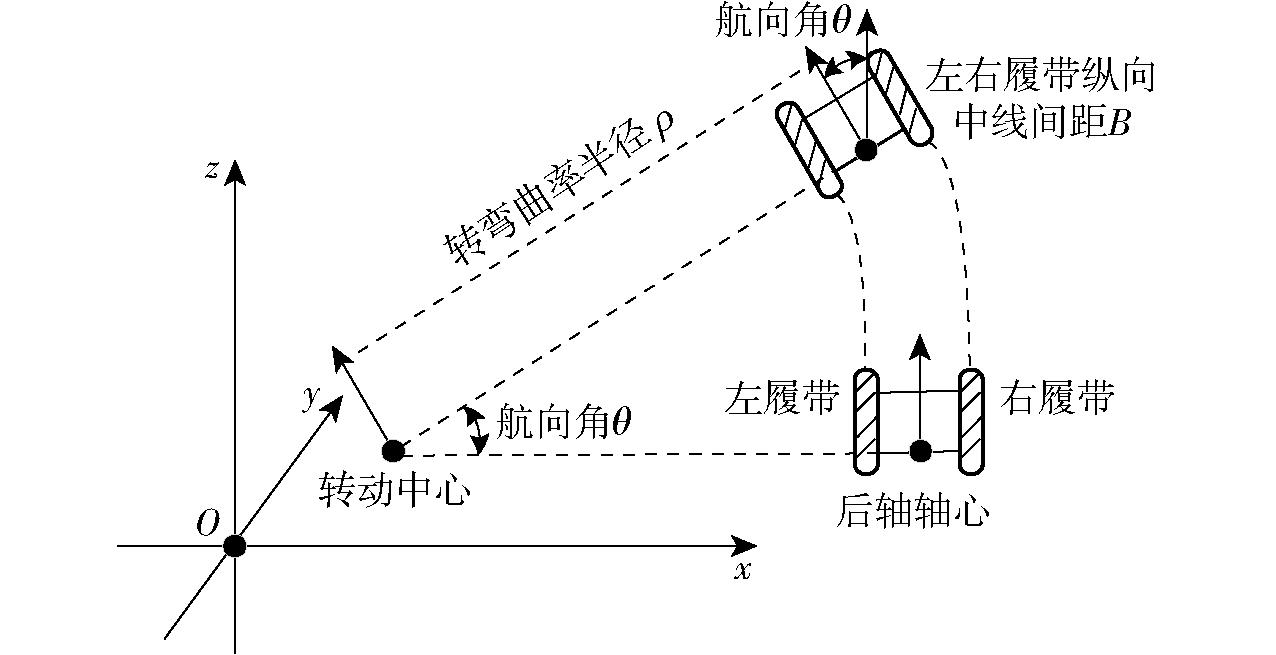
图5 果园履带机器人运动学模型
Fig.5 Kinematic model of orchard tracked robot
式中 ρ——底盘中心转弯曲率半径
B——左右履带纵向中线间距
θ——航向角
K——底盘中心转弯曲率
对于一次优化后的路径点,在换行转弯和行间避障处存在折线路径偏多、转弯曲率偏大等问题,因此,对不满足果园履带机器人曲率约束条件的路径点进行修正,通过调整转弯区域路径点来约束每次转弯角度,从而减小转弯曲率。
2.5 LM-BZS算法
为使路径更加平滑,利用贝塞尔曲线对转弯和避障路径中折线段进行平滑处理。贝塞尔曲线由于结构简单、平滑能力强而被广泛应用于路径二次优化中,由伯恩斯坦多项式(Bernstein polynomials)推导而来,伯恩斯坦多项式一般式可以表示为
![]()
(i=0,1,…,n)
(11)
式中 Bi,n(t)——伯恩斯坦基函数
n——贝塞尔曲线阶数
t——贝塞尔曲线参数
定义拟合空间的n+1个控制点,构成待优化的折线段路径,基于伯恩斯坦基函数Bi,n(t),1条n阶贝塞尔曲线的参数方程[27]可表示为
(12)
式中 Pi——贝塞尔曲线控制点坐标
利用贝塞尔曲线平滑路径时,随着控制点的增加,贝塞尔曲线次数会提高,导数零点可能会增加,引起曲线极值点增多,导致曲线振荡,曲线复杂程度会变高且容易出现龙格现象,使得平滑后路径与平滑前路径偏差过大,出现安全问题。为解决以上问题,本文采用LM-BZS算法进行二次优化处理。在换行转弯过程中,由于待平滑路径点构成的特征多边形相对固定,因此采用三阶贝塞尔曲线进行平滑处理;在行间避障过程中,由于避障路径点构成的贝塞尔多边形复杂多变,因此采用二阶贝塞尔曲线插值平滑优化,二阶贝塞尔曲线和三阶贝塞尔曲线公式[28]分别为
P(2,t)=P0(1-t)2+2P1t(1-t)+P2t2
(13)
P(3,t)=P0(1-t)3+3P1t(1-t)2+ 3P2t2(1-t)+P3t3
(14)
采用LM-BZS算法平滑折线路径的方式,可以降低曲线复杂度,提高路径规划效率,但需要保证各段曲线在连接点处具有G1连续[29],即各曲线段在连接点处具有公共的单位切矢(关于弧长的一阶导矢[30])。以拟合2段三阶贝塞尔曲线为例,给定 2条贝塞尔曲线的控制点列Pi(i=0,1,2,3),Qj(j=0,1,2,3),如图6a所示,为保证P(t)段与Q(t)段相连后在连接点处光滑,首先保证P(t)段终点和Q(t)段起点重合,同时确保2段曲线在连接点处一阶导数成比例,连接点处光滑充要条件为
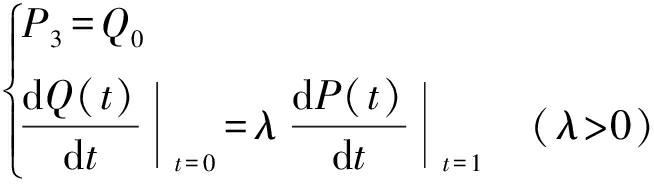
(15)
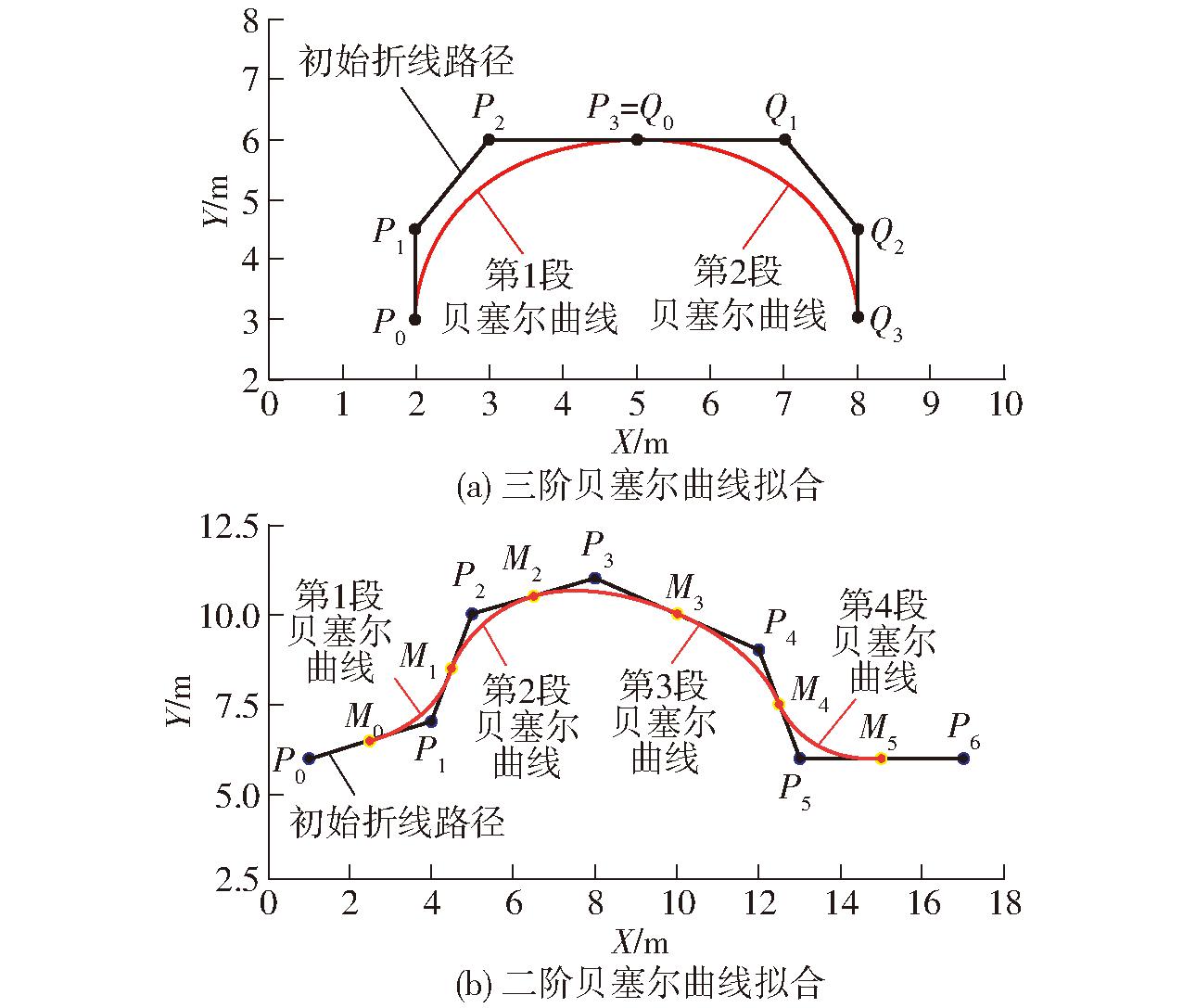
图6 低阶多段贝塞尔曲线拟合效果
Fig.6 Segmented Bezier curve fitting effect
式中 P3——P(t)段曲线终点
Q0——Q(t)段曲线起点
λ——连接点处一阶导数比例系数
对式(11)两边求导得到伯恩斯坦基函数递推公式为
![]() =n{Bi-1,n-1(t)-Bi,n-1(t)}
=n{Bi-1,n-1(t)-Bi,n-1(t)}
(i=1,2,…,n)
(16)
由式(12)两边求导可以得到n阶贝塞尔曲线一阶导数方程,将式(16)代入一阶导数方程可求出贝塞尔曲线一阶导数方程
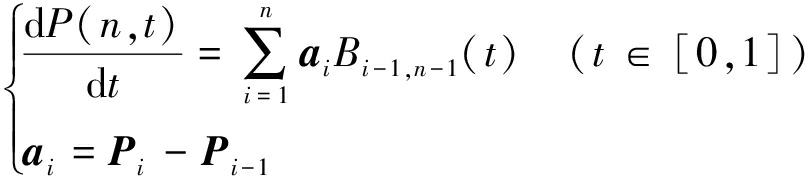
(17)
式中 ai——贝塞尔多边形边向量
由式(17)可分别计算出P(t)段曲线终点和Q(t)段曲线起点的一阶导数,将其代入式(14)中可以得到P3和Q0点重合,P2、P3、Q1 3点共线,即贝塞尔多边形通过贝塞尔曲线分段平滑后进行拼接,其在连接点处有公共的切矢方向,重复处理其他换行转弯折线,将平滑后曲线拼接到原路径中,即完成对换行转弯部分的二次优化处理。
在行间避障过程中,由于障碍物复杂,所规划路径形状存在多样性,因此选用3个控制点的二阶贝塞尔曲线对避障绕行区域进行平滑处理。在图6b所示局部路径中,Pi(xi,yi)为避障路径点,Mj为PiPi+1段中间点且j=i+1,其坐标表达式为
(18)
式中 τ——贝塞尔曲线拼接平滑度
τ越大,相邻曲线拼接后平滑度越高,但当τ>1时,随着τ的增大,相邻2段曲线相交后将产生尖峰,不符合履带机器人转弯曲率约束条件,因此取τ=1。
二阶贝塞尔曲线能够拟合3个点,以2个中间点和1个避障路径点组成一段贝塞尔多边形的控制点列,并将贝塞尔多边形上所有中间点和避障路径点按此标准进行组合,得到最终拟合点列矩阵,矩阵表达式为
(19)
PB=[PB0 … PBj … PBmax]T
(20)
对点列矩阵PB中每项做二阶贝塞尔曲线平滑处理,并以Mj+1为连接点拼接所有贝塞尔曲线得到完整避障曲线,替换规划路径中的折线避障路径,得到一条复杂度低且平滑的路径。
3 仿真试验
3.1 果园场景模拟地图
为验证本文算法在果园环境下路径规划的性能,基于Matlab将传统A*算法、高阶贝塞尔算法和本文算法在有、无障碍2种环境中进行对比仿真试验。考虑到机器人本体尺寸不仅会影响树行,障碍物的膨胀宽度还会对转弯曲率造成影响,因此设置机器人仿真模型尺寸(长×宽)为1.5 m×0.85 m,两侧履带中线间距为0.8 m,并和后续场地试验时机器人实际尺寸保持一致。
首先在已知果树和障碍物位置的情况下,根据树行分布特点设计果园场景模拟地图,如图7a所示。根据果园边界和果树位置确定整体搜索边界,同时为解决果树离散性问题,根据果树直径和树行长度对树行做拟合处理并对树行进行横向膨胀,左右膨胀宽度为履带机器人宽度一半,最后将树行交错延长至果园边界形成弓字形作业走廊,红色和绿色区域分别表示起点和目标点,如图7b所示。
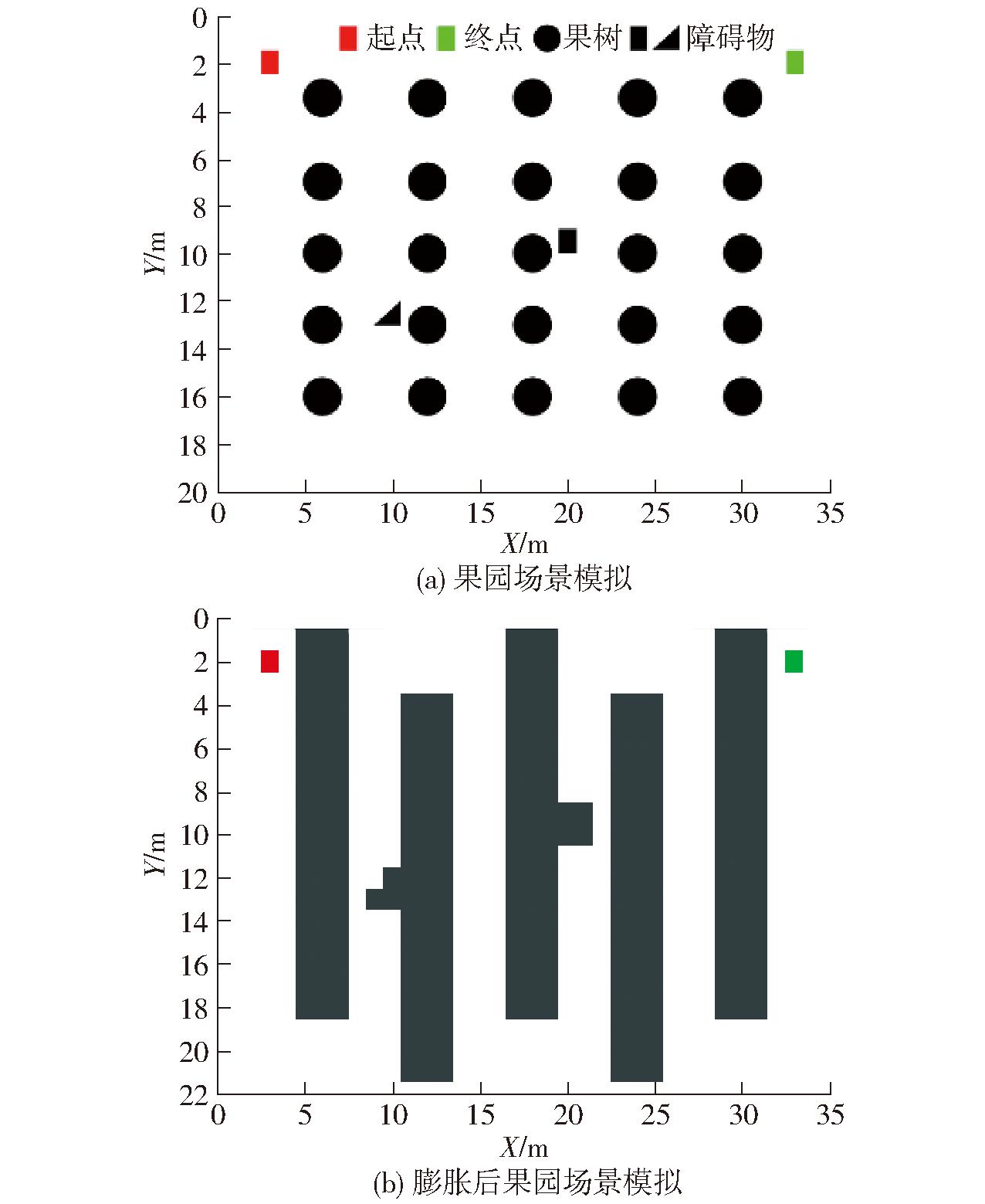
图7 果园模拟仿真图
Fig.7 Orchard simulation diagram
3.2 仿真试验环境
试验在Windows 11操作系统下进行,仿真软件为Matlab R2022a,处理器型号为12th Gen Intel(R) Core(TM) i7-12700F 2.10 GHz,显卡型号为Nvidia GeForce RTX 3060,6 GB显存,计算机运行内存为16 GB。
3.3 改进A*算法参数设置与验证
仿真试验中,改进A*算法权重函数w(n)中的权重比例系数a取6.67,树行区域路径点水平平移权重εx取1.382,竖直平移权重εy取1.081,中线避障路径点x轴方向偏移权重α取±1.1、β取±0.6、γ取±0.3,连接点处一阶导数比例系数λ取1,贝塞尔曲线拼接平滑度τ取1。
在图7所示仿真地图中使用改进A*算法探索路径,由于探索范围变大,探索方向始终根据目标点相对于初始节点位置不断调整,结合启发函数权重值对非必要节点的过滤,在兼顾探索最优路径的同时显著提升路径搜索效率,生成的初始路径如图8a所示。基于路径平滑和曲率约束对原始路径进行二阶段优化处理,第1阶段将树行间路径点进行中线避障投影处理,无障碍和有障碍初步优化路径如图8b、8c所示;第2阶段针对折线段偏多、折线角度偏大的换行转弯和行间避障区域分别采用三阶贝塞尔曲线和二阶贝塞尔曲线进行优化处理,无障碍和有障碍二阶段优化路径如图8d、8e所示。通过对比图8可知,经二阶段优化后的改进A*算法,可以生成更加平滑且满足最大曲率约束的作业轨迹,更符合果园履带机器人的实际作业要求。
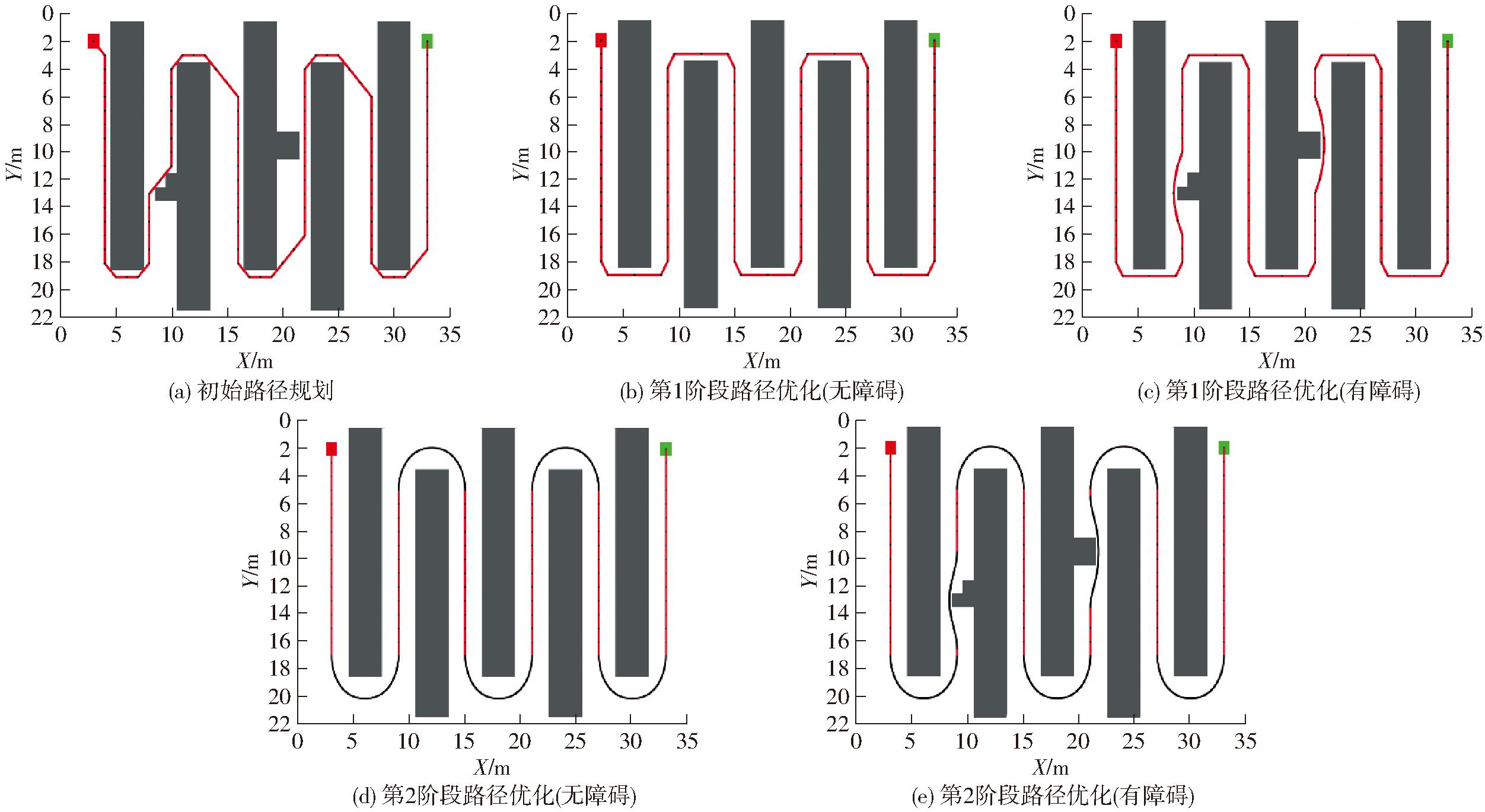
图8 路径规划仿真结果
Fig.8 Path planning test diagram
由表2可知,传统A*算法和本文算法100次独立运行仿真结果表明,在无障碍果园环境中,本文改进算法路径搜索时间相较于传统A*算法平均减少76.75%,路径规划速度是传统A*算法的4.3倍,算法迭代次数减少5.90%,节点评估数量比A*算法减少36.68%;在有障碍环境下,搜索时间平均减少86.40%,路径规划速度是A*算法的7.4倍,算法迭代次数减少10.48%,节点评估数量减少39.37%。由表2可知,本文改进算法在减少节点评估数量、规划路径速度和降低内存占用方面效果显著,且在复杂环境下更容易找到最短路径。
表2 算法性能比较结果
Tab.2 Algorithm performance comparison results
环境算法迭代次数节点评估数量搜索时间/s无障碍传统A∗算法322257613.55本文算法30316313.15有障碍传统A∗算法315252012.43本文算法28215281.69
由表3可知,在无障碍果园环境下,由于本文算法对改变航向部分路径进行平滑处理,虽然优化后的路径长度有所增加,但在转弯处最大曲率比传统A*算法降低47.22%,比高阶贝塞尔算法降低39.12%,所生成路径的平均曲率比传统A*算法减少45.81%,比高阶贝塞尔算法减少18.94%;在有障碍环境下,本文算法所生成轨迹只在换行转弯和行间避障附近存在曲率波动,其中最大曲率仍然出现在换行转弯处,同时由于高阶贝塞尔曲线具有较多的控制点和参数,导致平滑后曲线复杂度较高,在行间避障过程中产生较大的曲率波动。经本文算法优化后的路径,平均曲率相较于传统A*算法和高阶贝塞尔算法分别降低56.98%、27.81%,在无障碍树行中仍保持直线轨迹,从表现形式来看,本文算法可以有效减小转弯曲率。
表3 2种环境下路径曲率对比
Tab.3 Comparison of path curvature between two environments
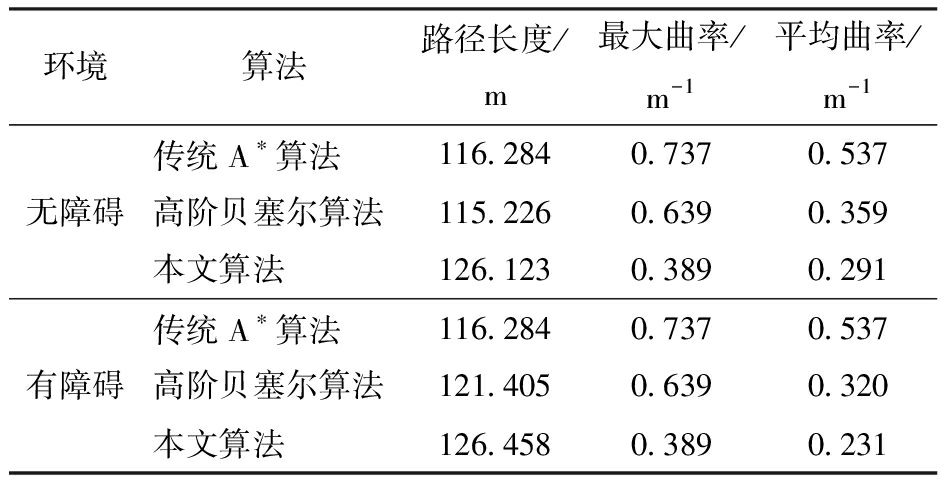
环境算法路径长度/m最大曲率/m-1平均曲率/m-1传统A∗算法116.2840.7370.537无障碍高阶贝塞尔算法115.2260.6390.359本文算法126.1230.3890.291传统A∗算法116.2840.7370.537有障碍高阶贝塞尔算法121.4050.6390.320本文算法126.4580.3890.231
图9a为传统A*算法、高阶贝塞尔算法和本文算法在无障碍环境中所生成路径的曲率随轨迹变化曲线,可以看出,本文算法比传统A*算法和高阶贝塞尔算法具有更小的曲率波动且有一定规律,波动主要出现在换行转弯处,基本满足最大曲率约束;图9b为有障碍环境中3种算法曲率随轨迹变化曲线,在该环境中,改进后算法所生成的路径满足果园履带机器人作业最大曲率约束,在25、70 m附近的波动是行间避障路径引起的。
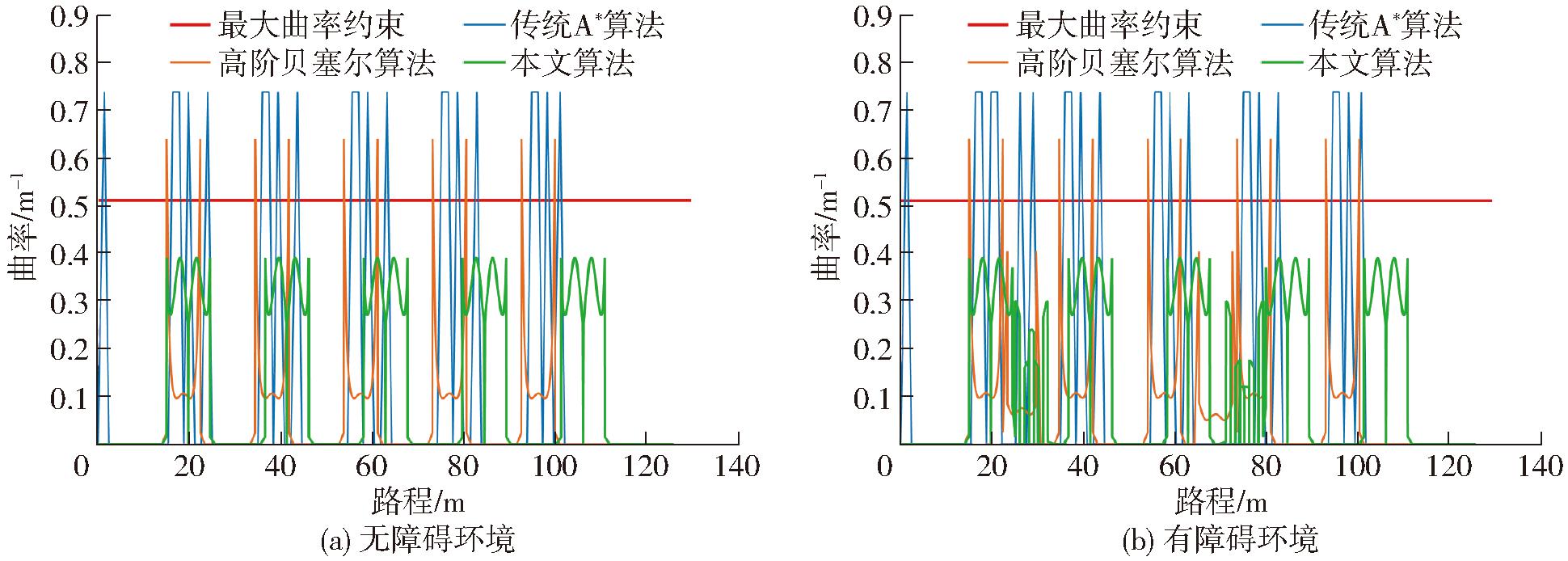
图9 果园环境下路径曲率对比
Fig.9 Comparison of path curvature in orchard environment
3.4 轨迹跟踪仿真验证
根据果园履带机器人模型在Matlab中选择纯跟踪轨迹跟踪算法进行仿真试验[31],设定左、右两侧履带转速nL、nR为3 000 r/min,减速器传动比itr为40,履带驱动轮圆心离地距离lq为0.242 m,机器人运行速度为0.83 m/s,前视距离权重为0.1,前视距离为0.8 m。利用路径跟踪算法根据规划的全局路径生成参考跟踪路径,观测其横向误差。在无障碍和有障碍2种果园环境中,分别对高阶贝塞尔算法优化路径和本文算法优化路径进行跟踪仿真试验,结果如图10、11和表4所示,高阶贝塞尔算法优化路径由于转弯曲率过大导致跟踪轨迹横向误差偏大,影响果园履带机器人实际作业效率。通过本文算法优化路径,可以显著减小横向误差,提高机器人作业稳定性。
表4 仿真履带机器人轨迹跟踪误差
Tab.4 Lateral error of track tracking of simulated tracked robot m

环境算法最大横向误差平均横向误差标准误差无障碍高阶贝塞尔算法0.3700.1070.040本文算法0.1850.0380.024有障碍高阶贝塞尔算法0.4240.1160.036本文算法0.1850.0460.023
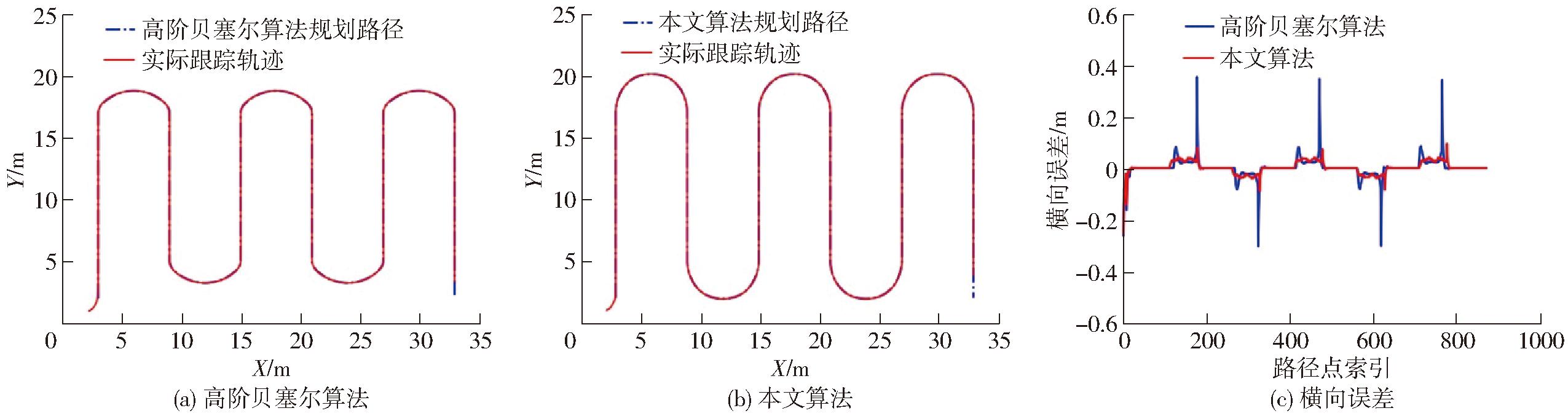
图10 无障碍环境下轨迹跟踪结果
Fig.10 Trajectory tracking results in barrier-free environment
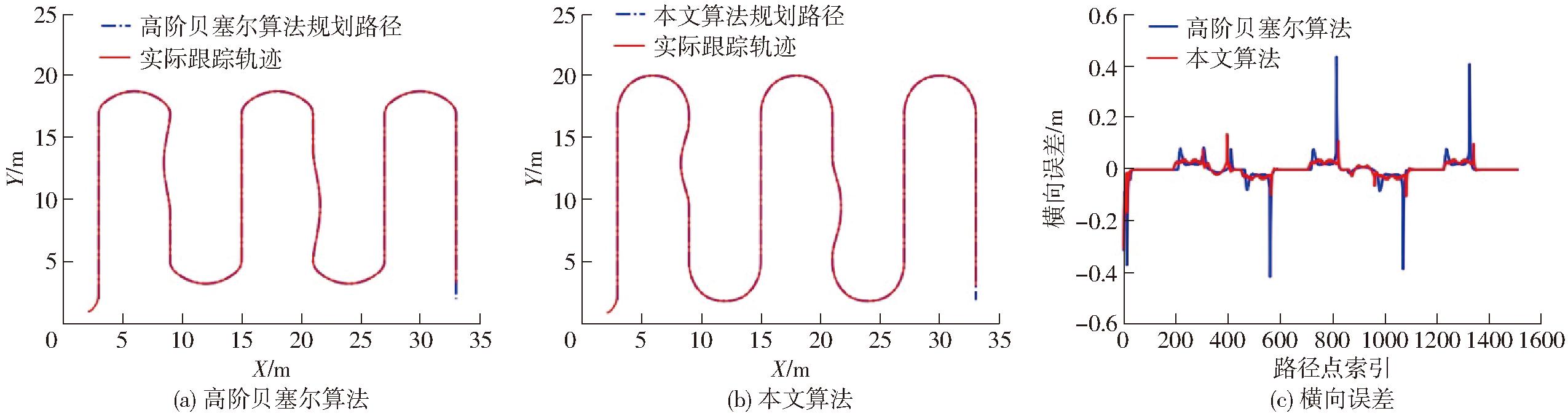
图11 有障碍环境下轨迹跟踪结果
Fig.11 Trajectory tracking results in obstacle environment
4 试验
4.1 试验平台
本文算法验证使用果园差速履带机器人作为试验平台,如图12所示。果园履带机器人主要由差速履带机器人底盘、工控机(处理器为英特尔酷睿八代i7-8700,装载Ubuntu 18.04 LTS操作系统)、组合导航系统(北斗星通组合导航系统C200)、三维激光雷达传感器(RS-LIDAR-16型,速腾聚创)组成。其中,差速履带机器人底盘为直流无刷电机驱动,两侧履带中心间距0.8 m,最大车速0.83 m/s,最小转弯半径0.75 m。基于机器人操作系统(Robot operating system,ROS)使用Python和C++语言编写跟踪控制代码并生成控制机器人的运动指令,通过CAN总线与底层建立系统通信,实现对果园履带机器人的行为控制。
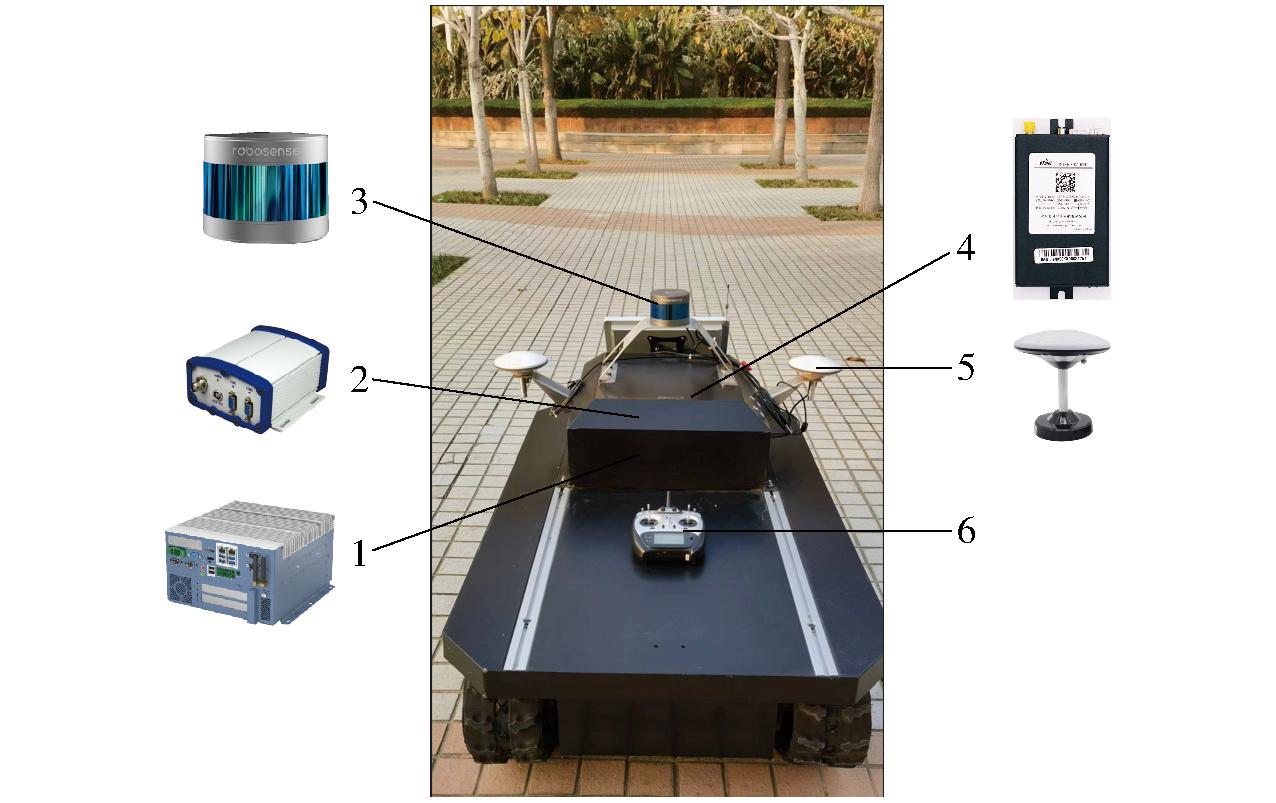
图12 果园履带机器人
Fig.12 Orchard crawler robot
1.工控机 2.北斗星通组合导航系统C200 3.三维激光雷达传感器 4.4G DTU模块 5.GPS定位天线 6.遥控发射机
4.2 试验与结果分析
试验场地位于山东农业大学紫叶李树林(36.194 430 9°N,117.112 047 2°E),如图13所示。模拟果园场景中,共有5列树行,平均每列树行长21 m,每列树行包括5株果树,同一树行中果树平均株距2.96 m,树行间距平均为6 m。对树行进行膨胀处理并添加边界约束形成弓字形作业走廊。采用纯跟踪算法控制果园履带机器人分别对有、无障碍果园环境中不同路径进行跟踪试验,同时计算实际跟踪轨迹与目标路径的横向误差和航向偏差作为评价指标。

图13 跟踪试验场景图
Fig.13 Testing scene of tracking experiment
在无障碍环境下,分别对2种贝塞尔优化算法生成的路径进行跟踪试验,并利用北斗星通导航系统实时采集履带机器人的位置信息,通过Matlab计算生成实际跟踪路径和目标路径,效果如图14所示。对比图14a、14b可知,2种算法优化后路径在直线跟踪时,由于曲率无明显变化,实际行驶轨迹与目标路径较为贴合;而在换行转弯时,经本文算法生成路径曲率波动较小,跟踪误差和航向偏差与高阶贝塞尔算法相比明显减小,行驶过程中最大横向误差为0.428 m,平均横向误差为0.232 m,平均航向偏差为11.06°。
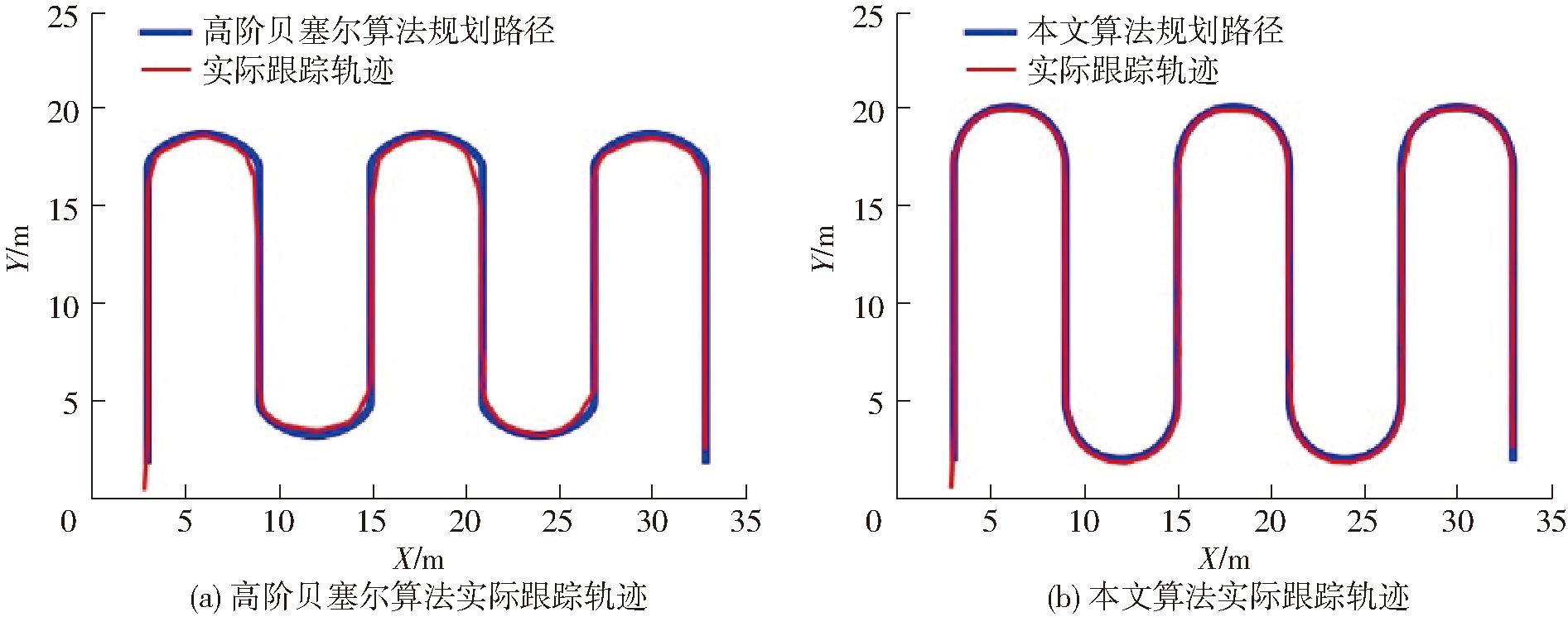
图14 无障碍环境下轨迹跟踪效果
Fig.14 Trajectory tracking renderings in barrier-free environment
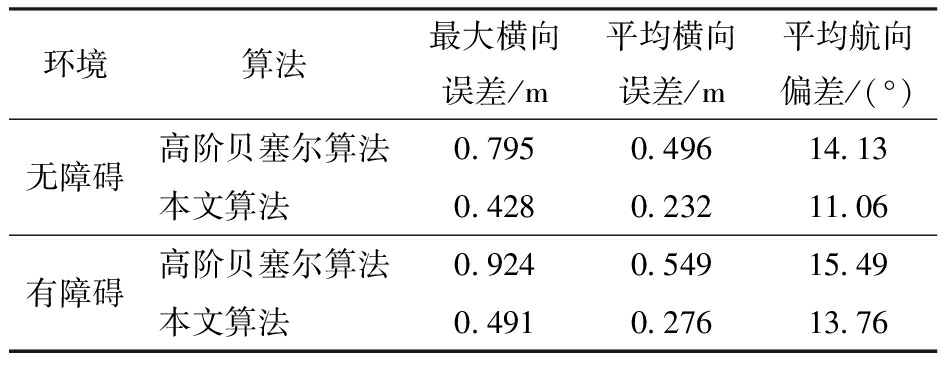
有障碍环境中,2种贝塞尔算法生成路径的跟踪试验效果如图15所示,相较于高阶贝塞尔算法,本文算法行驶轨迹跟踪误差更小,行驶过程中最大横向误差为0.491 m,平均横向误差为 0.276 m,平均航向偏差为13.76°。2种作业环境中行驶轨迹均符合果园履带机器人作业要求,轨迹跟踪效果如表5所示。
表5 果园履带机器人轨迹跟踪效果
Tab.5 Trajectory tracking effect of orchard crawler robot
环境算法最大横向误差/m平均横向误差/m平均航向偏差/(°)无障碍高阶贝塞尔算法0.7950.49614.13本文算法0.4280.23211.06有障碍高阶贝塞尔算法0.9240.54915.49本文算法0.4910.27613.76
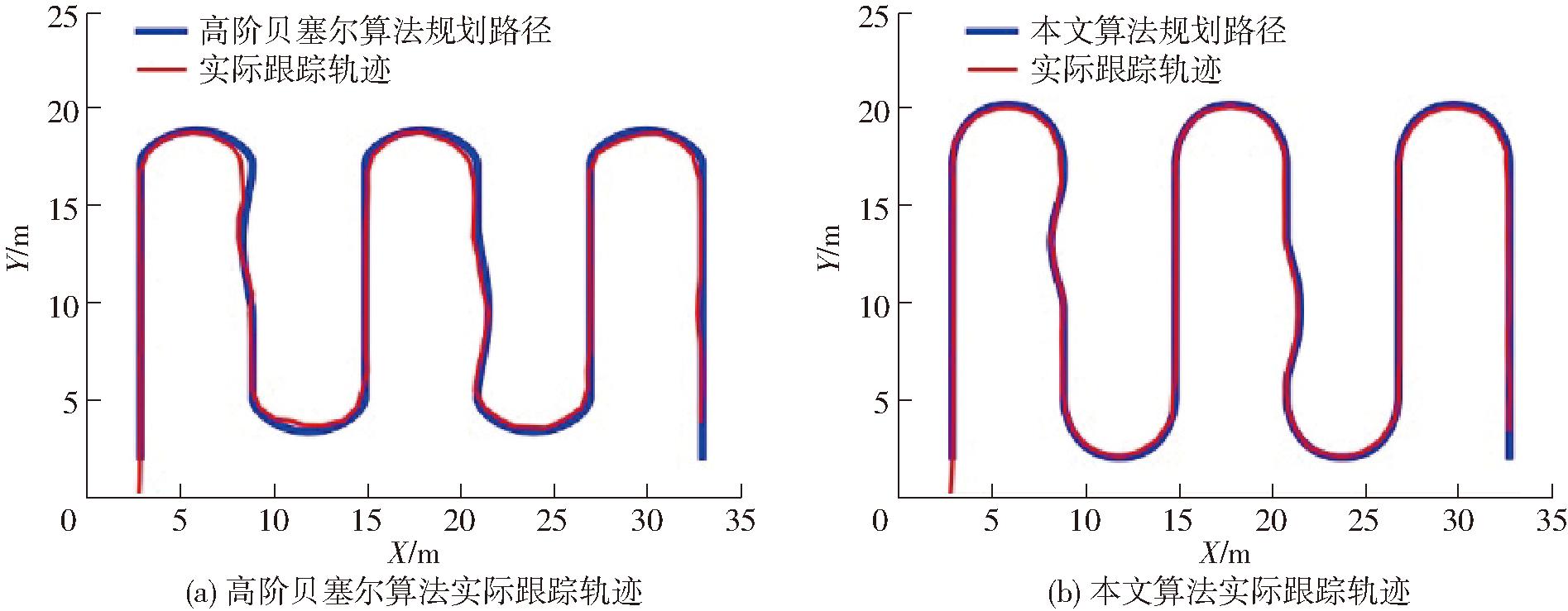
图15 有障碍环境下轨迹跟踪效果
Fig.15 Trajectory tracking renderings in obstacle environment
5 结论
(1)针对传统A*算法搜索效率低的问题,提出了一种改进A*的全局路径规划算法,相较于传统A*规划算法,在无障碍环境中,改进算法节点评估数量减少36.68%,搜索时间减少76.75%;在有障碍环境中,改进算法节点评估数量减少39.37%,搜索时间减少86.40%。
(2)搜索路径成功后,针对规划路径折线段多、折线角度大、作业不稳定等问题,提出了一种根据树行位置修正路径点并结合LM-BZS算法,生成符合果园履带机器人行驶条件的精准平滑轨迹,轨迹仅在换行转弯和行间避障过程出现路径弯曲现象,在无障碍环境中,生成路径最大曲率为0.389 m-1,平均曲率为0.291 m-1;在有障碍环境中,最大曲率为0.389 m-1,平均曲率为0.231 m-1,符合果园履带机器人运动学约束。
(3)场地试验结果表明,果园履带机器人在对本文算法生成路径跟踪行驶时,在无障碍环境中,最大横向误差为0.428 m,平均横向误差为0.232 m,平均航向偏差为11.06°;在有障碍环境中,最大横向误差为0.491 m,平均横向误差为0.276 m,平均航向偏差为13.76°,符合果园履带机器人作业精度要求。
[1] 刘成良,贡亮,苑进,等.农业机器人关键技术研究现状与发展趋势[J].农业机械学报,2022,53(7):1-22.
LIU Chengliang, GONG Liang, YUAN Jin, et al. Current status and development trends of agricultural robots[J].Transactions of the Chinese Society for Agricultural Machinery,2022,53(7):1-22. (in Chinese)
[2] 沈跃,张亚飞,刘慧,等.农业装备自动控制技术研究综述[J].农业机械学报,2023,54(8):1-18.
SHEN Yue, ZHANG Yafei, LIU Hui, et al. Research review of agricultural equipment automatic control technology[J].Transactions of the Chinese Society for Agricultural Machinery,2023,54(8):1-18. (in Chinese)
[3] 刘正铎,张万枝,吕钊钦,等.基于非线性模型的农用车路径跟踪控制器设计与试验[J].农业机械学报,2018,49(7):23-30.
LIU Zhengduo, ZHANG Wanzhi, LÜ Zhaoqin, et al. Design and test of path tracking controller based on nonlinear model prediction[J].Transactions of the Chinese Society for Agricultural Machinery,2018,49(7):23-30. (in Chinese)
[4] 张万枝, 白文静, 吕钊钦, 等. 线性时变模型预测控制器提高农业车辆导航路径自动跟踪精度[J]. 农业工程学报, 2017, 33(13): 104-111.
ZHANG Wanzhi, BAI Wenjing, LÜ Zhaoqin, et al. Linear time-varying model predictive controller improving precision of navigation path automatic tracking for agricultural vehicle[J]. Transactions of the CSAE, 2017, 33(13): 104-111. (in Chinese)
[5] 周俊,何永强.农业机械导航路径规划研究进展[J].农业机械学报,2021,52(9):1-14.
ZHOU Jun, HE Yongqiang. Research progress on navigation path planning of agricultural machinery[J].Transactions of the Chinese Society for Agricultural Machinery,2021,52(9):1-14. (in Chinese)
[6] 刘天湖,张迪,郑琰,等.基于改进RRT*算法的菠萝采收机导航路径规划[J]. 农业工程学报, 2022, 38(23): 20-28.
LIU Tianhu, ZHANG Di, ZHENG Yan, et al. Navigation path planning of the pineapple harvester based on improved RRT* algorithm[J]. Transactions of the CSAE, 2022,38(23): 20-28. (in Chinese)
[7] 曹如月,张振乾,李世超,等.基于改进A*算法和Bezier曲线的多机协同全局路径规划[J].农业机械学报,2021,52(增刊):548-554.
CAO Ruyue, ZHANG Zhenqian, LI Shichao, et al. Multi-machine cooperation global path planning based on A-star algorithm and Bezier curve[J].Transactions of the Chinese Society for Agricultural Machinery,2021,52(Supp.):548-554. (in Chinese)
[8] 劳彩莲,李鹏,冯宇.基于改进A*与DWA算法融合的温室机器人路径规划[J].农业机械学报,2021,52(1):14-22.
LAO Cailian, LI Peng, FENG Yu. Path planning of greenhouse robot based on fusion of improved A* algorithm and dynamic window approach[J].Transactions of the Chinese Society for Agricultural Machinery,2021,52(1):14-22. (in Chinese)
[9] 杨桂华,卫嘉乐.基于改进A*与DWA算法的物流机器人路径规划[J].科学技术与工程,2022,22(34):15213-15220.
YANG Guihua, WEI Jiale. Logistics robot path planning based on improved A* and DWA algorithm[J].Science Technology and Engineering,2022,22(34):15213-15220. (in Chinese)
[10] 张伟民,张月,张辉.基于改进 A*算法的煤矿救援机器人路径规划[J].煤田地质与勘探,2022,50(12):185-193.
ZHANG Weimin,ZHANG Yue,ZHANG Hui.Path planning of coal mine rescue robot based on improved A* algorithm[J].Coal Geology &Exploration,2022,50(12):185-193. (in Chinese)
[11] 杨芳清,刘吉成.融合改进A*算法与动态窗口法的移动机器人路径规划[J].工业控制计算机, 2021, 34(5):106-108,112.
YANG Fangqing, LIU Jicheng. Path planning of mobile robot combining improved A* algorithm and dynamic window algorithm[J].Industrial Control Computer, 2021, 34(5):106-108,112. (in Chinese)
[12] 吴鹏,桑成军,陆忠华,等.基于改进A*算法的移动机器人路径规划研究[J].计算机工程与应用,2019,55(21):227-233.
WU Peng, SANG Chengjun, LU Zhonghua, et al. Research on mobile robot path planning based on improved A* algorithm[J].Computer Engineering and Applications,2019,55(21):227-233. (in Chinese)
[13] 李晓露,熊禾根,陶永,等.基于改进A*算法的移动机器人全局最优路径规划[J].高技术通讯,2021,31(3): 306-314.
LI Xiaolu, XIONG Hegen, TAO Yong, et al. Global optimal path planning for mobile robots based on improved A* algorithm[J]. Chinese High Technology Letters,2021,31(3):306-314. (in Chinese)
[14] 李二超,齐款款.贝塞尔曲线融合双向蚁群算法的移动机器人路径规划[J].陕西师范大学学报(自然科学版),2022,50(3):79-88.
LI Erchao, QI Kuankuan. Path planning of mobile robot based on Bessel curve and bidiredtional ant colony algorithm[J].Journal of Shanxi Normal University(Natural Science Edition), 2022,50(3):79-88. (in Chinese)
[15] WANG H, LOU S, JING J, et al. The EBS-A* algorithm: an improved A* algorithm for path planning[J].PloS One,2022, 17(2): e0263841.
[16] 张文,刘勇,张超凡,等.基于方向A*算法的温室机器人实时路径规划[J].农业机械学报,2017,48(7):22-28.
ZHANG Wen, LIU Yong, ZHANG Chaofan, et al. Real-time path planning of greenhouse robot based on directional A* algorithm[J].Transactions of the Chinese Society for Agricultural Machinery,2017,48(7):22-28. (in Chinese)
[17] FENG D, DENG L, SUN T, et al. Global path planning based on an improved A* algorithm in ROS[J].Lecture Notes in Electrical Engineering,2022,799: 1134-1144.
[18] WANG X, ZHANG H, LIU S, et al. Path planning of scenic spots based on improved A* algorithm[J].Scientific Reports,2022,12(1): 1320.
[19] 郝琨,张慧杰,李志圣,等.基于改进避障策略和双优化蚁群算法的机器人路径规划[J].农业机械学报,2022,53(8):303-312.
HAO Kun, ZHANG Huijie, LI Zhisheng, et al. Path planning of mobile robot based on improved obstacle avoidance strategy and double optimization ant colony algorithm[J].Transactions of the Chinese Society for Agricultural Machinery,2022,53(8):303-312. (in Chinese)
[20] 姚露,廖庆喜,沈文惠,等.基于Bezier曲线的油菜旋转盘式精量集排器设计与试验[J].农业机械学报,2022,53(7):56-66,83.
YAO Lu, LIAO Qingxi, SHEN Wenhui, et al. Design and experiment of spinning disc precision centralized metering device for rapeseed based on Bezier curve[J].Transactions of the Chinese Society for Agricultural Machinery,2022,53(7):56-66,83. (in Chinese)
[21] 陈凯,解印山,李彦明,等.多约束情形下的农机全覆盖路径规划方法[J].农业机械学报,2022,53(5):17-26,43.
CHEN Kai, XIE Yinshan, LI Yanming, et al. Full coverage path planning method of agricultural machinery under multiple constraints[J].Transactions of the Chinese Society for Agricultural Machinery,2022,53(5):17-26,43. (in Chinese)
[22] 张淼,潘林沛,阳清亮,等.基于斜率-截距校正算法的番茄营养液ISE监测[J].农业机械学报,2018,49(5):342-347.
ZHANG Miao, PAN Linpei, YANG Qingliang, et al. ISE monitoring of macronutrients in hydroponic tomato cultivation based on slope and bias correction method[J].Transactions of the Chinese Society for Agricultural Machinery,2018,49(5):342-347. (in Chinese)
[23] XU Lin, SONG Baoye, CAO Maoyong. A new approach to optimal smooth path planning of mobile robots with continuous-curvature constraint[J].Systems Science &Control Engineering,2021, 9(1): 138-149.
[24] 王猛,赵博,王长伟,等.基于高斯混合模型的履带拖拉机转弯半径控制方法[J].农业机械学报,2020,51(增刊):557-563.
WANG Meng, ZHAO Bo, WANG Changwei, et al. Method for controlling turning radius of crawler-type tractors based on GMM[J].Transactions of the Chinese Society for Agricultural Machinery,2020,51(Supp.):557-563. (in Chinese)
[25] 张泮虹,倪涛,赵亚辉,等.基于最优控制策略的复杂环境移动机器人轨迹规划[J].农业机械学报,2022,53(7):414-421.
ZHANG Panhong, NI Tao, ZHAO Yahui, et al. Optimal control-based trajectory planning method of mobile robot in complex environment[J].Transactions of the Chinese Society for Agricultural Machinery,2022,53(7):414-421. (in Chinese)
[26] DURAKLI Z, NABIYEV V. A new approach based on Bezier curves to solve path planning problems for mobile robots[J].Journal of Computational Science,2022, 58: 101540.
[27] MA Jianwei, LIU Yang, ZANG Shaofei, et al. Robot path planning based on genetic algorithm fused with continuous Bezier optimization[J].Computational Intelligence and Neuroscience: CIN,2020(1): 9813040.
[28] CHEN Te, CAI Yingfeng, CHEN Long, et al. Trajectory and velocity planning method of emergency rescue vehicle based on segmented three-dimensional quartic Bezier curve[J].IEEE Transactions on Intelligent Transportation Systems,2023, 24(3): 3461-3475.
[29] AL-MAYYAHI A, ALDAIR A A, RASHID A T. Intelligent control of mobile robot via waypoints using nonlinear model predictive controller and quadratic Bezier curves algorithm[J].Journal of Electrical Engineering &Technology,2020, 15(4):1857-1870.
[30] 杨洋,温兴,马强龙,等.基于贝塞尔曲线的动态识别区农机避障路径实时规划[J]. 农业工程学报, 2022, 38(6): 34-43.
YANG Yang, WEN Xing, MA Qianglong, et al. Real time planning of the obstacle avoidance path of agricultural machinery in dynamic recognition areas based on Bezier curve[J]. Transactions of the CSAE, 2022, 38(6): 34-43. (in Chinese)
[31] 贺静,何杰,罗锡文,等.基于多传感器融合的水稻行识别与跟踪导航研究[J].农业机械学报,2022,53(3):18-26,137.
HE Jing, HE Jie, LUO Xiwen, et al. Rice row recognition and navigation control based on multi-sensor fusion[J].Transactions of the Chinese Society for Agricultural Machinery,2022,53(3):18-26,137. (in Chinese)