农业装备行驶滑动辨识与控制研究现状与展望

近年来,随着各种传感器和执行器的发展,农业自动化取得了长足的进步,其中自动驾驶系统等自动化技术的应用,使人们看到了自动化农业生产的广阔前景,相比于传统的农业生产技术,农业自动化技术在降低生产成本,减少对体力劳动的依赖,提高产品质量方面具有极大的优势[1]。目前农业自动驾驶系统的精度已经达到了厘米级[2],然而,现有的系统大多只有在正常行驶较少发生滑动的状态下才能实现可接受的精度以提供自动导航操作。当发生滑动时,将无法保证可靠的精度,特别是在潮湿或倾斜的田地上保持曲线路径跟踪时,由于滑动现象的存在,将产生较大的偏差。行驶机构的滑动通常被分为滑转和滑移,在非理想条件下,滑移总是伴随着滑转同时产生。按照转向方式的不同,对于滑转与滑移有不同定义方式[3-5]:针对滑动转向的车辆,其受到前进推力时发生的滑动称为滑转,受到制动力时发生的滑动称为滑移;针对差速转向的车辆,低速侧为滑移,高速侧为滑转。在农业环境中,当发生严重滑转时,意味着牵引力严重缺失,车轮可能发生严重沉陷情况甚至会导致永久沉陷,发生较低程度的滑转时会导致车辆滞后于目标位置;当发生滑移时,不会直接影响行驶功能,但会导致车辆偏离已规划路径,无法准确达到目标航向点,作业时可能对作物造成损伤。由于滑动现象具有随机性、时变性和突变性,目前尚无法完全对其进行精确预测与控制。

滑动现象一方面会造成作业过程中产生大量作业疏漏区域,另一方面不确定的滑动现象使行驶机构处于不可控状态,阻碍了种植、中耕管理和收获等需要精准作业环节的农业装备信息化及智能化进程。因此,针对农业装备行驶滑动机理进行研究,探索出行之有效的滑动辨识方法,并以此优化农业装备行驶效果,为农业装备的行驶控制提供技术支撑,对于农业装备自动化发展具有重要意义。

本文从滑动力学特性、滑动辨识方法和考虑滑动的路径跟踪控制3方面,综述农业装备行驶滑动辨识与控制研究进展,分析农业装备行驶滑动辨识与控制技术未来的发展趋势,以期为农业装备智能化发展提供参考。

1 农业装备行驶滑动力学特性

农业装备与土壤之间的力学特性,是研究农业装备行驶滑动现象的基础,用于农业生产的土壤通常要求有一定的含水率作为作物生长的必需条件。然而,在此条件下作业机具在行驶作业的过程中会因为重力作用产生沉陷,行驶机构对接触面上的土壤进行剪切,土壤抵抗变形产生行驶阻力。当土壤达到极限强度时会发生破碎,机具产生滑动现象,严重时导致作业机具无法工作。因此,对于滑动力学特性的研究,归根结底是对土壤能否具备机具行驶所需承载能力的研究。

1.1 农业装备沉陷与滑动特性

区别于坚实地面的滑动,在农业环境中讨论农业装备的滑动时,由于轮壤互作导致的沉陷问题是最重要也是最复杂的问题。土壤沉陷会增加农业装备的行走阻力,减少其牵引力。农业装备在松软土壤中运动时,可能发生两种不同类型的沉陷:一种是由接地压力产生的静沉陷,与土壤坚实度有关;另一种是由于推力不够或土壤在水平方向变形而产生的滑转沉陷。与滑移和滑转类似,在农业装备行驶中,静沉陷总是伴随着动沉陷,一般很难将静沉陷和动沉陷区别开来,许多研究工作者曾对静沉陷(Zs)作过讨论,最典型的是BEKKER[6]的沉陷公式

式中 P——垂直载荷,kg/m2

Kc——土壤内聚力,kg/mn+1

Kφ——内摩擦变形模量,kg/mn+2

B——加载区域较小尺寸,m

n——土壤变形指数,根据环境不同取0～1

除此之外,BEKKER还提出过一种半经验方法,通过试验证明最大剪切强度及垂直载荷与相应变形及滑转沉陷之间的关系近似表示为

式中 Pcrit——承载能力,kg/m2

τmax——最大剪切强度,N

j——土壤变形量

Zj——滑转沉陷量,m

其物理意义是,如果车辆载荷P小于土壤承载能力,就不会出现由滑动而引起的变形Zj,但是经试验证明,该公式仅对于内聚性土壤正确,对于疏松的摩擦性土壤则不完全正确。

土壤的沉陷并不完全由车辆载荷导致,接地面积下方由于履刺或轮刺的“挖土作用”而引起的沉陷过程,比公式中假定的条件更为复杂。在《地面-车辆系统导论》[6]中,BEKKER提出了履刺或轮刺从水平位置到达沉陷深度沉陷公式

式中 Ze——履刺或轮刺挖掘沉陷量,m

h——履刺或轮刺高度,m

式(3)表明,挖掘深度在开始滑转时很小,当i=50%时达到履刺或轮刺高度,当i=100%时深度猛增到无限大。

除了履刺或轮刺的“挖土作用”而引起的土壤沉陷过程,农业装备在作业时通常存在悬挂作业机具的场景,此时作业牵引力对滑动同样产生了影响,此时下陷量可以用滑转线性函数表示为

式中 Z0——作业牵引力沉陷量,m

ψ——土壤内摩擦角,(°)

由于农业装备滑动与沉陷的影响因素较为复杂,通过力学分析的方法通常仅能针对某一影响因素进行分析,并且并不适用于所有土壤类型。

1.2 轮式农业装备滑动力学特性

针对轮式农业装备滑动产生的条件,设车轮在土壤中滚动时,土壤受到载荷的压缩时在水平和垂直方向位移X、Y与作用力存在比例关系

式中 PX——载荷作用于水平方向的力,N

PY——载荷作用于垂直方向的力,N

AX、AY——土壤比例常数,随土壤物理机械性质而不同

当车轮(假设为刚性)在土壤上滚动而引起变形时,如图1所示。

用θ表示在车轮与土壤接触的任一点上垂线与法线之间的夹角,则作用力法向和切向分力为

式中 Fn——法向作用力,N

Ft——切向作用力,N

一般来说,在车轮与土壤的接触点,存在3种不同的情况:

(1)车轮在土壤上纯滚动时,没有滑移或滑转,则有

式中 f——车轮沿土壤滚动时的摩擦因数

在没有滑动的接触时,车轮上任一点的速度与土壤内相当点的速度相等。若用V0表示车轮中心的线速度,用ω表示车轮角速度,r表示车轮半径,并采用XY坐标系统,将车轮任一点的速度投影在坐标轴上,可以得到

式中 VX——车轮速度在X方向分量,m/s

VY——车轮速度在Y方向分量,m/s

X、Y可以表示为时间t的函数:X=f1(t)、Y=f2(t),对其进行微分可得对应的速度为

式中 VX′——土壤切向变形速率,m/s

VY′——土壤垂向变形速率,m/s

纯滚动时车轮边缘线速度和相对应的路面上点速度相等,即

此时,轮胎边缘上的点与路面之间的相对速度为零,做纯滚动运动。

(2)当车轮处于滑移状态时,需要满足VX>VX′,即车轮与路面接触的点应该满足

滑动摩擦因数和摩擦角之间满足

式中 φ——摩擦角,(°)

μ——滑动摩擦因数

将式(14)代入式(13)可得

由式(15)可知,当车轮滑移时,轮胎胎面上的反作用力与法线偏离一个摩擦角,方向与车轮转动方向相同,如图2所示。

(3)当车轮处于滑转状态时,车轮相对滑动向后,即向着车轮中心运动相反方向,此时存在不等式

将式(14)代入式(17)可得

由式(18)可知,当车轮处于滑转状态下,路面给车轮的反作用力与法线之间偏离一个摩擦角φ,方向与车轮相对转动方向相反,如图3所示。

1.3 履带农业装备滑动力学特性

由于履带农业装备利用差速转向的特性,加之履带与土壤之间的相互作用,其滑移和滑转现象相对于轮式农业装备更加频繁。研究履带在土壤中的滑动,首先需要确定履带推进力并在此基础上附加土壤作用。

农业装备作业环境面对的土壤大多是可压缩的(如水田、耕后农田等),其剪切强度在达到最大值后随变形的增加下降到常值,即剩余强度,因此可以应用库伦公式

式中 C——土壤内聚力,N

通过式(19)可以预测履带在理想条件下能够发挥的最大驱动力。

履带与地面接触面积如图4所示,则总驱动力H等于单位剪切强度沿接触表面的积分,即

式中 b——土壤-履带接触宽度,m

L——土壤-履带接触长度,m

由于农业装备总重量W必须保持平衡

式(22)表明,由于土壤剪切强度使履带产生的最大驱动力是由2部分组成的:一部分是由土壤内聚力产生的,它与履带接地面积有关;另一部分是由土壤摩擦力产生的,它与农业装备重量成比例。但式(22)仅适用于在最佳滑动条件下产生的最大驱动力,对于其他滑转率i,许多学者提出了不同的数学模型来描述驱动力与滑动之间的关系[7]。KACIGIN修改了前人方程,得出相对准确的剪切变形方程

式中 τ——剪切应力,N

τm——剩余剪切应力,N

Kτ——土壤剪切变形模量,Pa

fmax——最大摩擦力,N

fm——剩余摩擦力,N

由此得到驱动力与滑动的关系为

从式(24)中可得,履带滑动与土壤本征参数密切相关,不使用计算机方法很难精确确定。

1.4 滑动力学特性研究现状

由于滑动现象的普遍存在,国内外均针对滑动力学特性进行了广泛研究。在国外,从20世纪50年代开始,BEKKER等[6]已开始对行驶机构的地面力学性质进行系统研究;WONG[8]在BEKKER研究的基础上于1989年出版了《THEORY OF GROUND VEHICLES》,推动了地面力学的进一步发展,是现有多种地面力学模型的理论基础。LYASKO[9]建立了履带滑动、沉陷预测模型,研究了滑动、沉陷和履带车辆行驶阻力的关系,结果表明滑移率在0～33%范围内变化时,沉陷量随滑移率线性增加;AZIMI等[10]将弹塑性理论应用于履带地面行驶力学中,建立了履带-地面互作关系分析模型;LI等[11]对比分析了3种不同的压力-沉陷模型,推导了最大剪应力与法向压力的关系,模拟了地面沉陷量与加载时间、加载压力,以及牵引力与滑移的关系;RAYMOND等[12]采用库仑侧向土压力理论和无源土破坏模型建立行驶机构-土壤力学模型,计算了履带底盘在软土中的受力分布,并评估了该方法在软土地面上的先进性和局限性;SPITERI等[13]提出了履带软地面稳态转向运动模型的解析方法,建立了履带沉陷量和通过性预测模型;TANG等[14]提出了不含履带车辆结构参数的履带-地面系统模型,分析了不同结构的履带在松软地表的动力学状态,研究了影响转向滑移量的主要因素;EDWIN等[15]建立了便于快速开展仿真分析的行驶机构单刚体动力学模型,通过计算履带与地面接触点处土壤的位移,实现了单刚体行驶机构模型在土壤中的沉陷模拟;NICOLINI等[16]提出了基于多体动力学的履带-土壤压缩模型,应用该模型分析了履带对土壤压力的分布状态。

在国内,毕松等[17]建立了滑动转向轮式机器人坡道稳态动力学方程和轮胎实时驱动力估计方法,基于轮胎利用率构造轮胎驱动力最优实时分配模型,提高了轮胎附着裕量和姿态控制稳定性。李军等[18]提出了履带-地面相互作用的三维模型分析方法,基于三维力学状态计算履带沉陷量和牵引力,试验表明该方法对沉陷量和牵引力的预测偏差小于20%。迟媛等[19]研究了履带差速转向时载荷比与土壤下陷、滑移、转向系数的关系,分析了这些参数对差速转向履带转向性能的影响。杜永浩等[20]基于离散元法构建了低含水率软地面土壤数值仿真模型,研究了土壤附着力沿履刺排列的变化规律,探究了土壤颗粒在动态荷载下非连续的机理。孙中兴等[21]结合半经验法与土槽实验法,分析了履带行进过程中土壤剪切流动及滑移线分布规律,提出了滑转流动导致的土壤流失量计算方法,探究了履带应力分布。姚禹等[22]建立了履带-地面耦合系统数学模型,分析了地面参数和履带行驶机构参数对履带-地面间摩擦力和侧面推土力的影响,并基于Recurdyn软件构建了履带-地面耦合系统仿真模型。

国内外学者针对不同行驶机构的结构特点和行驶地面环境,建立了多种行驶机构与地面系统模型,用于描述行驶机构与土壤的相互作用关系并以此对行驶机构与土壤行驶滑动力学特性进行分析,但是所提出的力学特性研究均局限于特定环境下并且很难直接转化为滑动观测量。除此之外,由于履带车辆在行驶时的滑动现象相对于轮式车辆更加突出,目前的研究主要聚焦于履带的行驶滑动研究,然而在一些农业复杂环境,例如水田、沙地和泥地等,轮式车辆同样会发生严重的行驶滑动现象,履带车辆的行驶滑动模型、机理与轮式车辆也有较大差异。此外,在农业环境中,水田属于高含水率的泥水混合土壤,行驶机构将产生更大幅度和更高频率的行驶滑动,其作用机理也更加复杂,对于水田中的行驶滑动,目前研究较少。综上所述,在滑动力学特性研究方面,国内外学者已经取得了一定进展,但现有的研究并未涵盖所有农业环境和农用车辆。

2 滑动辨识方法

根据现有研究滑动辨识的主要方法,本文将行驶机构的滑动辨识研究分为基于数学模型的滑动参数估计和基于数据驱动的滑动辨识,其中基于数据驱动的滑动辨识又可以分为滑动感知和精确定位两种,如图5所示。

2.1 基于数学模型的滑动参数估计

滑动是车轮与土壤之间复杂相互作用的结果,建立具有滑动变量的精准运动学方程和动力学方程可以用来估计车轮滑动,建立车体三维运动学模型可以估测车体滑动[23-24]。其中具有代表性的成果为SEEGMILLER等[25-26]于2014年提出基于运动学模型的滑动预测方法。该研究考虑了非零车轮滑移关系,并将其与经典的车轮-地面接触模型联系起来,同时在计算时摒除了传统对车轮滑移值进行估测的方法,而是直接对车体滑动进行计算,并以此建立了一种新的运动学方法来预测车体滑动,通过归一化方法对传统滑动运动学模型进行了改进,获得

式中 S——车轮滑移率

a——滑移率与滑移角归一化极限

fx、fy、fz——接触力在各方向的分量,N

Vx——x方向速度分量,m/s

vx、vy——车体相对于地面的速度分量,m/s

在公式中加入车轮的惯性效应(重力、加速度)和耗散效应(如滚动阻力)后,使用空间向量代数来计算车体惯性力为

式中 g——重力加速度,m/s2

vb——车体空间速度,m/s

车体复合空间惯量

fb——车体惯性力,N

为了保证公式重心的一致性,将fb和vb转换为

其中重心的位置需要通过计算Plǖcker变换

和空间惯性力

得到。此外vcg和fcg都有其线性和角度分量

如图6所示,将车体滑移速度根据纵向角γlon、横向角γlat和滑移角γang方向上的单位向量进行参数化,得到

其中z为法向力方向。式(29)中的p1和p3是式(25)中对滑移与车轮受力的直接模拟,p2考虑滚动阻力,它防止车辆以恒定速度滑行,由于纵向滚动阻力与法向力成正比,因此两者被抵消。式(30)中p4解释了过度转向及转向不足的行为,这与横向加速度成正比,p5解释了滚动阻力左右不对称现象,p6解释了滑转现象。

该模型是在多位前人的相关研究的基础上发展而来。虽然该模型没有加入二阶惯性效应,无法计算如锁紧制动器打滑等现象,但它能计算正常运行或接近稳态条件下的滑动情况,已能够较为准确地预测滑动。

BALARAM[27]将滑动行为结合到扩展卡尔曼滤波框架中,对巡视器Rocky-7中每个运动链的动作进行适当的最小二乘平均;SHILLER等[28]基于滑动和路径数据,针对履带车辆给出了土壤特性的参数估计方法;LE等[29]基于SHILLER的方法,设计出履带车辆土壤特性参数的实时在线计算方法。此后,众多学者开始对行驶机构滑动的参数估计进行了研究;IAGNEMMA等[30]通过对土壤内聚力和土壤内摩擦角的参数估计,提出了一种最小二乘在线计算方法;SONG等[31]将牛顿-莱福逊和最小二乘法相结合,对土壤参数进行了评估,并通过设计非线观测器对滑动进行参数评估;SCHEDING等[32]利用增强型的卡尔曼滤波器对滑动现象进行了参数估计;ZHOU等[33]利用4个不同的滤波器对行驶机构的位姿和时变参数进行了评估,同时还对履带车辆非线性参数评估方法进行了比较;DAR等[34]则利用卡尔曼滤波的方法对噪声进行了消除,并准确估计出模型车的轨迹、方向以及打滑率等变量;CHWA[35]提出一种模糊自适应跟踪方法,采用模糊干扰观测器对干扰进行观测补偿,基于移动机器人打滑的一般形式,推导出与状态相关干扰的运动学方程,并设计了模糊自适应观测器和参数适应律,用以估计在运动学和动力学上的状态相关扰动。

虽然基于数学模型的滑动参数估计已得到相当程度的完善,但所提及的文献多见于早期文献中对滑动现象进行观测和评估,大多不具有实时性,并且适用场景相对单一。总的来说,对于滑动发生后的补偿控制,基于数学模型的滑动参数估计能够为其提供精准的计算和论证,是滑动辨识研究中的一种重要工具和补充。

2.2 基于数据驱动的滑动辨识

所谓滑动辨识是指行驶机构在发生滑动现象时,通过检测行驶机构的位姿变化参数对滑动进行评估或预测的技术,即通过各种传感器、技术和系统直接或间接地获得行驶机构的运动参数及定位。本文将基于数据驱动的滑动辨识分为滑动感知和精确定位两种技术方法,其中滑动感知主要是通过建立地形几何与滑动之间映射关系的方式实现滑动辨识,侧重点在于对滑动现象的观测;精确定位则是通过精确获得行驶机构的实时位置和姿态实现滑动辨识。通过总结两种方法的优缺点,以期得到有益于滑动辨识研究的未来发展方向。

2.2.1 基于数据驱动的滑动感知

基于数据驱动的滑动感知方法本质上是以特征值数据为输入、滑动观测量为输出,通过不同算法得到的滑动模型。表1对目前基于数据驱动的滑动感知研究进行了整理。

目前基于数据驱动的滑动感知在农业装备领域涉及较少,主要集中在月球车等装备中。LINDEMANN等[36]对车辆在斜坡上的滑动行为展开研究,所用行驶机构为MER模型车(如图7a所示),试验场地为喷气推进实验室(JPL)的室内可变地形倾斜平台,设置试验坡度为0°～20°,结果显示滑动是地形坡度的高度非线性函数,在20°工况时,滑移率高达91%;ANGELOVA等[37-38]利用局部加权线性回归和人工神经网络建立了地形几何与滑动之间的非线性回归映射关系,立体图像作为输入预测滑动数值,得到的模型具有良好的滑动预测性能,在多种地形上进行了离线测试,预测误差约为20%,研究所用行驶机构为Rocky8和LAGR模拟巡视机器人,分别如图7b和图7c所示,试验场地为土壤、砂土、砾石和木屑等多种室外地形;GONZALEZ等[39]将滑动值估计问题转化为分类问题,以惯性测量单元的信号为输入特征,通过ANN、支持向量机(Support vector machines,SVM)、自组织映射(Self-organizing mapping,SOM)等多种机器学习算法实现滑动等级(低滑、中滑、高滑)评估,其分类方式为低滑(滑转率小于0.3)、中滑(滑转率为0.3～0.6)、高滑(滑转率大于0.6),但该分类依据需随环境不同而有所变化;为了提升算法精度,GONZALEZ等[40]随后对特征信号选取、惯性测量单元放置位置等细节问题展开研究,研究所用行驶机构为与NASA合作开发的LATUV模块化多功能平台,如图7d所示,试验场地为宾夕法尼亚州的某处矿山;DIMASTROGIOVANNI等[41]以驱动力矩、纵向力、摩擦因数为输入,通过SVM构建地形分类器,并将地形类型和滑动水平标签进行关联,沙地类型对应高滑移,石块类型对应低滑移,如图7e所示;ROTHROCK等[42]基于地面试验分别建立在沙地、小石块、基岩等多种地形条件下的滑移-坡度模型,之后基于相机图像对前方地形进行分类与坡度识别,并借助地面滑移-坡度模型进行滑移率预估;CUNNINGHAM等[43]提出可以基于车辆滑动数据对滑动模型进行修正以提高在沙地中的估测性能;文献[44-45]提出一种评估车辆行驶风险的评价指标,通过数据驱动建立了非参数滑移与坡度间的关系,如图7f所示。

综合上述研究可知,基于数据驱动的滑动感知方法正在成为滑动研究的普遍趋势。数据驱动不需要建立具体的函数模型,因此对于农业复杂环境,将同样具有良好的适应性。如表1所示,按照输入特征值的来源,可将基于数据驱动的滑动感知分为两类[46]:

(1)基于外部信息的滑动感知:以视觉图像信息作为特征输入,提取坡度等地形信息。虽然滑动与地形信息高度非线性相关,但是这种关系远远不能进行精确的滑动感知,且同样受限于图像处理算法的复杂性,无法实现实时的滑动感知。

(2)基于本体信息的滑动感知:以IMU信号、车轮转矩、视觉等信息作为特征输入。基于本体信息的模型不依赖于外部环境,提升了辨识算法鲁棒性,且不具有图像处理的复杂性,运算速度高,可用于实时的滑动感知。

2.2.2 基于数据驱动的精确定位

当农业装备行驶作业时,若能获得其本身的实时精确定位,发生滑动时通过获得该时间段内位姿变化,同样能够实现实时的滑动辨识。基于数据驱动的精确定位是通过精确获得行驶机构的实时位置,间接获得行驶滑动数据。在农业领域中具有代表性的有车轮里程计、惯性导航系统(INS)、全球导航卫星系统(GNSS)、激光传感器、视觉传感器等。在本节中通过分析各传感器的优缺点,讨论应用于滑动辨识的可行性。

估计移动机器人位置的最简单和最广泛使用的方法是车轮里程计。它通过计算与地面接触的车轮转数来估计轮式车辆的位置。编码器测量得到车轮转数,可以精确地转换为相对于地面的线性位移[47],如图8所示。

随着传感器技术的发展,出现了众多将各种传感器与车轮里程计相结合实现定位的新技术。GERSDORF等[48]利用平行于车轮平面的两轴加速度计数据和垂直于车轮平面的单轴陀螺数据,设计了一种卡尔曼滤波算法用于估计车体的位置、速度和加速度,但没有考虑航向变化,只适用于行驶机构的直线运动。DU[49]将旋转调制技术用于基于MEMS的车内转台固定的车辆导航,研究了误差抵消效应以及旋转导致的额外传感器误差,分析了旋转对增强惯性导航系统可观性的作用,并融合GNSS通过车载旋转转台试验证明了旋转NS在GNSS中断场景下的精度。BUSSMANN等[50]将文献[51-52]提出的6参数模型应用于轻型巡视器,在Mount Etna上进行的测试结果表明,由此产生的车轮里程计测量精度得到了显著改进。

车轮里程计是一种相对定位技术。当车轮打滑时将造成位置漂移和不精确,这导致随着时间推移误差累积[53-54]。因此,车轮里程计中的平移和旋转误差会随着行驶距离成比例增加,但是车轮里程计的优势在于其原理和结构简单并且价格便宜,同时车轮里程计允许高采样率,使其表现出良好的短期准确性[55-56]。

(2)惯性导航系统(INS)

INS是一种相对定位技术,它提供物体相对于已知起点、方向和速度的位置和方向,图9所示是INS的核心部件惯性传感器(IMU)。INS可以作为一种导航辅助设备,使用计算机、运动传感器(加速度计)和旋转传感器(速率陀螺仪)来连续计算行驶机构的位置、方向和速度。INS的优势在于其独立性,即它不需要外部参考[57-58]。然而INS极易产生漂移累积,因为速度和位置变化的计算是通过对加速度相对于时间进行连续积分来实现的,加速度计数据需要积分两次才能得到位置,而速率陀螺仪数据只需积分一次就可以跟踪方位。因此,加速度和角速度测量中的任何小误差都被合成大的速度误差,这些误差又被合成为更大的位置误差[57-59],并且误差是累积的,随着时间而增加,这是导致惯性传感器不精确的主要因素。因此,需要用另一个定位系统的输入来定期校正位置,单独的INS不适合长时间的定位,通常用于补充其他定位系统,以提供比使用任何单一系统可能达到的更高的精度[56]。此外,若要实现精确的惯性导航,需要高成本的设备,使得该方法对于商业应用来说是不可行的解决方案[47,55]。

(3)全球导航卫星系统(GNSS)

GNSS是一种基于卫星的导航系统,允许用户精确地确定他们在地球表面任何地方或稍高于地球表面的位置[60-61]。GNSS用于定位时,是一种相对定位技术,需要使用两个或多个接收器同时跟踪相同的卫星,其精度通常在10 m以内,差分GPS(DGPS)和实时动态GPS(RTK-GPS)的发明极大提高了GNSS的精度(图10),并且使其能够在厘米甚至毫米量级的户外空旷环境中定位。

GNSS的主要优点是不受时间误差累积的影响,并具有长期稳定性,但是它仅在天空视野清晰的区域有效,在室内、封闭、地下和水下空间不可用。GNSS的局限性还包括卫星信号阻断导致的中断、偶尔的高噪声内容、多路径效应、低带宽以及干扰或堵塞,GNSS信号中断容易发生在城市隧道、峡谷、和其他被GNSS信号拒绝的环境和受限的地方[57,61-63]。

激光传感器可用于与定位相关的多种应用中,它是一种用于距离测量的遥感技术,通过向目标发射激光,然后接收分析反射光。基于激光的距离测量依赖于飞行时间法(TOF)及相移技术。激光传感器在TOF系统中,发出短激光脉冲,测量它返回的时间,这种类型的传感器通常被称为激光雷达或光探测和测距传感器(LiDAR)。在相移系统中,传输的是连续信号,将返回信号的相位与同一信号源产生的参考信号进行比较,目标的速度和到达的距离用多普勒频移来测量[64-65]。激光雷达可以与GPS和INS集成,以提高户外定位应用的精度。激光雷达的缺点是解决方案非常昂贵。此外,计算两次激光扫描之间最佳匹配的迭代方式增加了数据分析的计算成本,在实时应用时可能会导致响应问题。另外,当材料对激光透明时,例如玻璃,扫描可能会失败,因为这些表面上的反射会产生错误的数据[64-66]。

精确的激光传感器价格昂贵,惯性传感器虽然可以测量传感器瞬时精确的角速度和线速度,但是随着时间的推移,测量值有明显的漂移,使得计算得到的位姿信息不可靠。而视觉传感器由于其低廉的成本和长距离较为精准的定位精度,在众多传统里程计中脱颖而出。近年来,随着同步定位与地图绘制(SLAM)技术的发展,许多研究人员对基于计算机视觉的定位系统表现出兴趣,因为计算机视觉定位系统比其他基于传感器的定位系统更加鲁棒和可靠。由相机捕获的图像可以提供大量的信息用于多种目的,包括定位、导航等。与其他传感器相比,光学相机是低成本的传感器,可以提供大量有意义的信息。而且视觉信息是被动的,即当使用光学相机时,定位系统不会被一些常见的因素所干扰而导致定位的失效[59,67]。基于视觉的移动机器人导航是计算机视觉和机器人研究的主要目标之一[68],这种方法是一种有效定位移动机器人的非接触方法[69]。对于自主导航,机器人需要跟踪自己的位置和运动,视觉里程计(Visual odometry,VO)通过分析由摄像机捕获的图像序列来提供行驶机构位置增量的在线估计[63,68]。相对来说,基于视觉的里程计是一种廉价的替代技术,并且在很多情况下比GPS、INS和车轮里程计等传统技术更精确[70]。除此之外,VO在成本、可靠性和实现复杂性之间有一个很好的平衡[71],它可以通过使用消费级相机而不是昂贵的传感器或系统来估计机器人的位置[71-72]。然而,图像分析通常计算量很大,在视觉定位中,计算包括几个步骤,即获取摄像机图像、提取几个图像特征(边缘、角、线等)、图像帧之间的匹配,以及通过计算帧之间的像素位移来计算位置。此外,视觉算法对操作和环境条件高度敏感,例如闪电、纹理、全天的照明变化、图像中模糊的存在、阴影的存在以及地面上水或雪的存在,这些都会对图像分析产生干扰。因此,视觉算法可能在某些条件下表现良好,但在其他环境条件下,则不一定能够很好地工作,从而变得不可靠[56]。

基于视觉的滑动估测按照参考对象的不同可以分为基于自然环境的滑动估测与基于轮地图像的滑动估测。基于自然环境的滑动估测通常由视觉里程计(VO)实现,如图11a所示,其工作原理是在行驶过程中,相机不断采集环境图像,通过连续的图像序列计算自身的位置与姿态的变化,并结合车轮转速信息进行滑转率判断[71,73]。该方法具有较高的滑移估测精度,但是在应用中具有一定的局限性:①其依赖于序列图像中周围环境信息的特征点匹配,对于特征点稀疏及阴影区域,行驶机构无法完成定位,进而无法判断滑移状态。②序列图像的特征点匹配工作计算成本较高,每次计算耗时为分钟级别[74],这使得基于视觉里程计的滑动估测数值仅可作为某一段行驶路径后的滑动真值,而无法实时估测监控车体滑动[63]。

邓宗全团队提出基于轮地图像中的车辙、车轮等信息进行滑移估测[75-76]。如图11b所示,通过单目视觉基于车辙间距判断无侧偏理想状况下的车轮滑转率,分析星球车车辙纹理的形成机理,建立了车轮轮刺空间轨迹方程[77-78],根据车辙图像的时域特征进行了滑移估测,并提出借助机器视觉提取车辙图像频域特征的技术,一定程度上提升了滑移估测算法的鲁棒性,估计误差约3%。文献[79-80]提出了通过高亮度车辙弱边界的车辙提取方法进行车轮线速度的估测,并结合利用追踪车轮标记点估测得到的车轮角速度进行车轮滑移估测。基于轮地图像的滑移估测方法相比于基于自然环境的滑移估测方法具有较好的鲁棒性,克服了地表特征点获取及对光照条件的依赖,且计算成本显著下降。

基于视觉的滑动辨识最突出优势在于能够用价格低廉的设备实现较为精确的滑动辨识,但是早期的视觉算法尚不成熟,计算成本过高,导致早期的文献均得出了视觉算法只能作为滑动估测的辅助手段,不能用于精准的滑动数值评估,无法实现实时的滑动观测。随着近年来视觉SLAM技术的发展,作为其前端的VO也得到了很大发展,将VO应用于实时滑动辨识研究也将具有极大的发展前景。

表2对常见的定位传感器的优缺点进行了分析和归纳。

针对农业装备行驶滑动辨识,最理想的情况是在发生滑动前进行预测,进而通过控制行驶机构来避免滑动或降低滑动导致的危害,然而由于滑动现象的随机性、时变性、突变性,该目标极难实现,因此对滑动现象更灵敏识别同时避免将自身正常移动的误识别成为研究重点。综上所述,通过数学模型的方式进行辨识较难满足实时性,通常需要大量的计算才能得出相应的结论,并不适用于滑动辨识这种具有瞬时性现象的观测,仅能作为一种理论补充;通过数据驱动的方法进行滑动辨识是目前较为流行的方式,具有一定的实时性和准确性,然而不同的数据驱动方法都有其优缺点,影响到滑动辨识的实时性和精确性。

3 考虑滑动的路径跟踪控制

由于滑动现象是在行驶过程中产生的,因此仅仅对行驶滑动进行实时辨识只是实现减少滑动危害的第一步,在此基础上,在发生滑动后对滑动及时控制或规避才能使其危害降至最低。由于大多情况下,滑移总是伴随着滑转同时产生,仅在实验室条件下存在纯滑移和纯滑转现象,并且在行驶滑动控制中,大多研究关注的是理论路径与实际路径的偏差,因此在本部分中不再将滑移和滑转分开讨论。

考虑滑动现象的突变性,对滑动的实时辨识涉及到大量的运算过程,因此在考虑滑动的控制系统研究中,可以分为滑动补偿控制和滑动预测控制两种,但由于滑动现象与行驶机构本身的状况(姿态/速度)、地形类型(岩石、基岩、土壤/沙土或它们的混合物)以及表面状况(例如压实度和积聚深度,土壤特性和轮土相互作用)相关,预测滑动十分困难。因此更多的研究侧重于在发生滑动后进行补偿,这一思路与路径跟踪的思路十分类似,均是在机具位置偏离预定位置后,通过控制机具回归理想位置的方式,实现行驶滑动控制,因此可以认为滑动补偿控制的理念是对路径跟踪控制方法的延伸,即当行驶机构发生滑动时,通过滑动辨识方法进行实时滑动辨识,之后通过高精度和高效的路径跟踪控制方法,实现对滑动的实时有效控制。

行驶机构的路径跟踪可以定义为在行驶机构上选取一个控制点,以跟踪与时间参数无关的几何曲线,即位置的空间序列(Xs,Ys)。在给定速度下,控制点Pc被指定为跟踪期望路径上的目标路径点Pd。通常假设纵向车速不变,设计侧向运动控制器,以使控制点与期望路径之间的侧向位移误差和航向角误差逐渐趋近于零。

基于路径跟踪控制方法的滑动补偿控制首先应用在移动机器人的滑动问题中,在文献[81-82]中,提出了只考虑滑行效应的移动机器人的控制方法。WANG等[83]提出了同时考虑滑移和滑转的轮式移动机器人模型,并根据行驶机构的可操作性分析了其可控性,除此之外,针对行驶机构在打滑情况下的路径跟随和跟踪还研究了相应的控制设计方法[18-19]。

根据系统模型和控制方法的不同,将现有考虑滑动的路径跟踪控制方案进行划分[84],包括几何学模型、运动学模型和运动学及动力学模型3种系统模型。

3.1 基于几何学模型

几何学模型是指行驶机构转向操纵时的几何关系,其中包括行驶机构与参考路径间的相对位姿关系和阿克曼转向几何关系,其具有简单实用和鲁棒性高的优点。基于几何学模型的跟踪控制经典算法主要有纯追踪算法和Stanley算法,其中Stanley算法相比于纯追踪控制算法更适用于较高车速的行驶工况,但是对期望路径的平滑程度要求较高,在道路曲率光滑性不理想的情况下容易出现车辆响应超调过大的问题,因此在农业环境下大多采用纯追踪算法。

纯追踪算法基本原理如图12所示,算法本质上可以理解为转向曲率ρ是关于侧向位移误差ye且增益系数为

的比例控制。在考虑滑动的路径跟踪控制方面,该方法在滑动发生后,是一种仅根据位置变化关系对滑动进行补偿的方法,其中更多的是对行驶机构位姿与转向几何关系的研究,与滑动本身的特性关联较少,此外该方法更适用于地形条件较好的环境中,在滑动频繁的复杂环境中存在滑动补偿失效或恶化的情况。

在农业装备行驶滑动方面,部分学者基于纯追踪算法进行了研究。柴善鹏等[85]设计了一种基于粒子群算法的纯追踪模型动态前视距离的确定方法,通过对农用车的位姿偏差进行定量分析,采用粒子群优化算法实时确定跟踪模型的最优前视距离,有效提高纯追踪模型的自适应能力,使其更适用于滑动等复杂场景。张文利等[86]将预测控制理论与模糊纯追踪模型相结合,提出了一种预适应路径跟踪控制模型,解决了传统跟踪控制算法存在的跟踪精度差、响应速度慢等问题,根据无人收获机的运动情况对参数进行动态调整,通过预测控制理论提前对跟踪量进行校正,前视距离的参数将根据跟踪期望路径的误差进行自适应调整,提高收获机的跟踪精度。WANG等[87]为了提高农业装备的鲁棒性,提出了一种由车载计算机、电子方向盘、转向角传感器等组成的自动导航系统,控制算法由纯追逐路径跟踪方法修改,能够根据不同的车速选择相适应的前瞻距离,采用具有滑移角的行驶机构动力学模型,试验结果表明,在田间以速度4.5 m/s进行作业时,横向误差约为3.3 cm,所提出的自适应前瞻距离自动导航算法对不同工作条件具有鲁棒性。

在几何学模型控制方法的应用上,由于农业环境的复杂性,针对农业装备的几何学模型控制以纯追踪算法为主。但是该方法并没有考虑行驶机构的动力学特性和转向执行器的动态特性,因此在发生滑动时,系统模型与实际行驶机构特性相差较大,容易导致跟踪性能恶化。

3.2 基于运动学模型

与依赖于行驶机构位姿关系和阿克曼转向的几何学模型不同,运动学模型进一步考虑了车辆的运动方程,但不涉及行驶机构本身物理性质(如质量等)和作用力。在基于运动学模型研究行驶机构运动控制问题时,通常假设行驶机构不存在侧滑,即质心侧偏角为零,满足非完整约束条件。如图13所示,可以在Frenet坐标系下建立运动学模型,将路径曲线表示为行进距离s的函数。描述车辆运动的参考坐标系可以根据算法设计需求选取,常用的还包括车辆坐标系和大地坐标系。

按照控制结构的不同,可以将基于运动学模型的控制方法分为链式变换、反馈线性化和模型预测控制。在考虑滑动的路径跟踪控制方面,基于运动学模型的方法在滑动发生后,不仅针对位置变化关系,同时根据车辆的运动关系对滑动进行补偿,相对于基于几何学模型的方法具有更好的补偿精度和鲁棒性。由于农业装备在农业环境中发生滑动时具有较大的速度和位姿变化,普遍采用模型预测控制的方法进行行驶滑动控制研究。该方法的原型为RAFFO等[88]基于离散线性化后的时变运动学模型,提出的广义模型预测控制路径跟踪控制方法,该方法能够在初始误差过大时采用纯追踪算法以避免小角度假设不成立导致的模型失配,但受限于当时嵌入式系统的计算能力限制,其试验结果仅适用于低速工况,之后一些研究针对该方法进行了相关应用和改进。

SONG等[89]考虑纵向速度和道路曲率对低速复杂驾驶条件下轨迹跟踪稳定性的影响,采用二自由度运动学模型设计了时变模型预测控制器,以改善无人设备低速通过曲率较大的急转弯路段稳定性,提高轨迹跟踪精度,试验结果表明,在复杂的驾驶条件下,被控的行驶机构在不同曲率的道路上跟踪的稳定性得到提升。LENAIN等[90]考虑了在实际工作条件下行驶机构的驱动轮与路面存在打滑的情况,通过对传统的运动学模型进行修改提出了一个拓展的运动学模型。在期望路径曲率变化较慢的情况下采用非线性控制算法,在驱动轮胎存在打滑的情况下能够减小跟踪误差;在曲率变化速度快的情况下引入预测控制算法,对由传感器延迟和行驶机构惯性导致的跟踪误差进行补偿。刘正铎等[91]设计一种基于非线性运动学模型的模型预测控制算法。将行驶机构的运动学模型的控制量作为目标函数,对各个参数变量设置约束条件,通过求解满足行驶机构速度约束和转向角约束的最优值问题得到可行解,控制行驶机构跟踪期望路径。郝思佳等[92]建立了一种农业装备二维三自由度运动学模型,采用模型预测控制算法,分别针对直线转弯、顺时针转弯和S弯等运动模式进行了仿真,仿真结果表明该方案在不同运动模式下的最大平均偏差为15.96 cm,成功解决了传统牵引式农业装备存在的曲线运动轨迹不一致的问题。CHO等[93]基于GPS/超声波传感器开发了喷雾机自主导航作业系统,基于超声波检测实现了避障识别并设计了规避路径,基于模糊控制和遗传算法设计了路径跟踪控制器,田间试验表明系统实现了自动避障功能。

在农业环境下,基于运动学模型的路径跟踪控制方法主要以模型预测控制和反馈线性化为主。该方法不依赖于行驶机构的动力学模型,简单实用,在中低速和小曲率工况下,通常具有较好的控制效果,但是在大侧向加速度工况下运动时,存在较为明显的侧滑,不满足非完整约束条件的前提假设,因此该方法并不适用于高速和大侧向加速度工况。

3.3 基于运动学及动力学模型

由于基于几何学或运动学模型的控制方法忽略了行驶机构的系统动力学特性,其适用工况具有较大的局限性。因此,为了获取更加精确的控制效果,尤其是在高速和大曲率工况下,有必要在路径跟踪控制设计时考虑行驶机构的系统动力学特性。在考虑滑动的路径跟踪控制方面,基于运动学及动力学模型的方法由于考虑了行驶机构的系统动力学特性,即使在高速行驶导致滑动距离较大或转向曲率较大时,依然能够针对行驶机构状态实现实时判断进而进行滑动补偿,因此该方法更适合应用于复杂环境中,但该方法也相对更为复杂。

按照控制结构的不同,可以将考虑动力学特性的跟踪控制算法归纳为两类:直接基于系统模型进行反馈控制;先根据运动学关系计算表征行驶机构运动的虚拟控制量如横摆角速度等,然后根据动力学特性进行跟踪。分层控制结构可以将行驶机构的高维非线性控制问题分解,同时也便于直接横摆力矩控制等传统动力学控制手段的扩展应用。若按控制方法不同,则可以将基于运动学和动力学模型的路径跟踪算法分为PID控制、全状态反馈控制、滑模控制、模型预测控制、鲁棒控制、自抗扰控制、微分平坦理论、模糊控制等[94]。在考虑滑动的路径跟踪控制研究中,主要采用的是模糊控制、全状态反馈控制、滑模控制、模型预测控制4种。

模糊控制是以模糊集理论、模糊语言变量和模糊逻辑推理为基础的一种智能控制方法,该方法能够在滑动发生时及时获得滑动状态情况,并通过模糊逻辑进行补偿控制。模糊控制虽不需要精确的系统建模,但模糊控制建立需要先验知识建立实用的规则库,并且缺乏理论上的稳定性证明。

在农业装备行驶滑动控制方面,王伟康[95]通过分析受田间滑移滑转等因素影响的底盘运动学模型,设计了底盘自动导航系统路径跟踪模糊控制算法,考虑转向系数的模糊控制器平均横向偏差为0.168 m。赵春召[96]对防滑转工况进行仿真分析, 考虑滑转率设计模糊控制器,将合成偏差和行驶速度作为模糊控制器输入,前视距离作为模糊控制器输出,解决纯追踪算法中前视距离难以确定问题。KAYACAN等[97]基于非线性最小二乘法实现行驶机构模型参数的辨识,设计了模糊控制路径跟踪控制器,开发了基于GNSS的导航控制系统,跟踪误差较大。吴才聪等[98]利用拖拉机与目标路径的实时位置误差设计模糊控制器,通过模糊控制算法对前轮转角进行补偿。孟庆宽等[99]通过改进粒子群优化算法实现了农业装备行驶机构模型参数的在线辨识,设计了自适应模糊控制器实现路径跟踪,在沥青路面速度0.8 m/s下,直线路径跟踪偏差为4.2 cm、曲线路径跟踪偏差为5.9 cm。

3.3.2 全状态反馈控制

全状态反馈控制是一种控制系统设计方法,其基本思想是在闭环控制系统中引入系统的内部状态变量作为控制变量,以改善控制性能。这种方法的优点是可以获得更好的控制性能,因为它可以更好地适应系统参数的变化,而且可以在系统出现干扰时仍然保持良好的控制效果,譬如在发生高滑或者剧烈的地形变化时对控制效果产生较大影响。具体来说,在全状态反馈控制中,控制器会获取系统的内部状态,并将其与期望的目标值进行比较,然后调整控制输入以达到预期的效果。此外,还可以使用滤波器或其他算法来处理噪声和其他干扰,以获得更加稳定和精确的控制效果。

在农业装备行驶滑动控制方面,LI等[100]采用分级控制的方式设计了路径跟踪控制装置,并设计了一种基于自适应模型控制的路径跟踪控制算法。一级控制器基于非线性运动学模型采用反馈线性化控制算法,二级控制器采用模糊控制器,能够自适应地调节系统的控制量,有效解决了非线性运动学模型存在的模型不够精确的问题。BELL[101]通过离线辨识确定了参数,设计了最优导航控制系统,在速度 1.8 m/s 下开展了田间试验,直线路径跟踪最大误差为10 cm,曲线路径跟踪误差为60 cm。张智刚等[102]以久保田插秧机为平台,基于RTK-GPS和INS组件设计车体航向最优估计算法,并基于纯追踪模型设计了直线路径跟踪算法,田间试验表明,直线追踪速度为0.75 m/s时,平均误差为10.4 cm,圆曲线跟踪行进速度为0.33 m/s时,平均偏差为 40 cm, 仿真和试验结果表明,该算法具有较强的速度自适应能力。胡炼等[103]研制了基于CAN总线的分布式插秧机导航控制系统。

全状态反馈控制本质上是针对线性系统的无约束优化方法,求解时假设控制量不受约束并且依赖于较为精确的数学模型,在参数时变和外部扰动存在时无法保证系统鲁棒性,因而在非线性特征显著的极限工况下跟踪控制精度会降低。因此在考虑滑动的控制上,一方面,该方法需要在已有精确滑动数学模型的基础上进行研究;另一方面,需要保证在控制过程中各种外参和因素没有发生较大变化,这些都极大增加了导航控制系统的搭建成本。

在运动控制中,考虑车辆相对于路径间的运动学关系和车辆非线性动力学后,其控制系统维度较高,针对这类高维非线性并且存在外部扰动和内部模型不确定性的被控对象,可以对高维状态空间降维,利用非线性控制理论有针对性地进行鲁棒性分析与控制。滑模控制的不连续性特性可以迫使系统按照预定“滑动模态”的状态轨迹运动,这种滑动模态是可以设计的且不受系统参数变化和扰动影响,因此从理论上来说,该方法比较适合在发生频繁滑动的环境中使用,也因为该特性,滑模控制方法在农业装备运动控制中被广泛使用。

在农业装备行驶滑动控制方面,ZHANG等[104]采用滑模控制算法来控制电机扭矩,使其快速响应车轮负载变化,根据计算出的最优滑移值调节电机输出,从而控制车辆滑移状态维持在高效牵引的范围内。WEN等[105]通过设计纯电动拖拉机的滑模函数和控制器参数调整,实现驱动电机扭矩的快速响应和精确控制,使得驱动轮的滑移率能够接近或维持在最优值,进而提升整体牵引效率和降低能耗。张婷[106]针对农业装备特定局部作业轨迹,考虑其特殊作业环境造成的滑移扰动问题,研究基于扰动估计的轨迹跟踪控制策略,设计集成有限时间扰动观测器和非奇异快速终端滑模(NFTSM)的轨迹跟踪控制策略。刘进一[107]针对拖拉机运动速度对拖拉机自动导航系统的稳定性影响,提出了基于横向位置偏差和航向偏差的联合滑模控制方法,分别在定速和变速条件下进行田间试验,试验结果表明最大位置偏差小于12.8 cm。BACKMAN等[108]设计了拖拉机滑移估计器,考虑了拖拉机滑动因素对拖拉机自动控制的影响,试验结果表明,加入车轮滑动因子的控制方法能有效提高轨迹跟踪精度。

滑模控制方法对参数不确定性和外部扰动具有强鲁棒性,适合用于考虑滑动的路径跟踪控制中,但是由于滑模控制会在有延迟或未建模的高频动态特性时产生抖动现象,一旦遇到传感器信号波动,或执行器控制效果不佳时,容易使车辆在运行过程中发生抖振,影响车辆稳定性。

3.3.4 模型预测控制

模型预测控制是一类特殊的控制。它的当前控制动作是在每一个采样瞬间通过求解一个有限时域开环最优控制问题而获得。过程的当前状态作为最优控制问题的初始状态,解得的最优控制序列作为当前控制动作或实际控制输入。剩余的控制序列则通常被丢弃,因为下一个采样瞬间会重新进行优化,基于最新的系统状态再次计算一个新的最优控制序列。这是它与使用预先计算控制律的算法的最大不同。本质上模型预测控制是求解一个开环最优控制问题。它的思想与具体的模型无关,但是实现则与模型有关。模型预测控制原理主要由以下部分组成:①预测模型,预测模型是模型预测控制的基础,能够根据历史信息和控制输入预测系统未来的输出。②滚动优化,模型预测控制通过使某项性能评价指标最优来得到最优控制量,这种优化过程不是离线进行的,而是反复在线进行的,这也是模型预测控制与传统最优控制的根本区别。③反馈校正,为了抑制由于模型失配或者环境干扰引起的控制偏差,在新的采样时刻,首先检测对象的实际输出,并利用这一实时信息对基于模型的预测进行修正,然后再进行新的优化。

由于农业环境下滑动具有动态变化特点,必须满足关键的安全约束和执行器约束等条件,而模型预测控制算法具有系统地考虑预测信息和处理多约束优化问题的能力,并且理论和计算能力的并行发展扩大了实时模型预测控制的应用范围,因此近年来学者们对基于模型预测控制的农业装备运动控制应用开展了诸多研究。

徐广飞等[109]搭建了农用拖拉机在田间工作的纵向跟随动力学模型,并提出一种农业装备分层控制架构,有效提高无人农业装备的响应能力,解决了无人农业装备设备跟随协同作业响应慢、跟踪控制困难等问题。张会琪等[110]考虑了模型预测控制器的输出量约束对路径跟踪控制的影响,选用二自由度的侧向动力学模型作为预测模型,对行驶机构在路径跟踪过程中的质心侧偏角和横摆角速度进行约束,确保行驶机构能够平稳可靠地跟踪目标路径。张万枝等[111]通过对二轮车运动模型离散化得到线性时变模型,基于预测控制理论设计了预测控制算法,以小型试验车为平台在平整草坪上进行了试验,速度为3 m/s时误差小于10 cm。王子杰[112]基于模型预测控制算法构建了考虑轮胎滑移影响的分层路径跟踪控制,分析喷雾机在直行和转弯过程中偏离期望路径的距离和驱动轮滑移率的变化情况,实现路径跟踪、车辆速度和轮胎滑移的有效控制。

对于模型预测控制而言,随着车辆动力学模型和约束的维度增加其优化求解的计算量增大,并且无人驾驶车辆的速度提升也会进一步增加优化求解的难度,因此计算的实时性是模型预测控制在运动控制上应用的主要技术瓶颈之一。另外,传统模型预测控制对系统不确定性的处理能力是有限的,当系统模型描述不准确或者存在外部扰动时,往往难以实现既定的控制目标。除此之外,证明模型预测控制算法的渐进稳定性较为困难,为了满足不确定性系统的控制需求,通常需要满足终端等式约束和终端域约束等条件。

目前对于农业环境下行驶滑动控制的研究已经取得了一定的发展,但仍有相关问题尚未得到很好解决:①现有研究大多集中在小侧向加速度的常规工况,对行驶机构在大侧向加速度的极限工况和曲率不连续、路面突变等复杂工况考虑不足,算法的适用性和鲁棒性尚缺乏足够验证。②现有研究大多针对农业环境的中低滑场景,而无法兼顾高滑场景,在发生瞬时大幅度滑动时,往往无法实现有效及时的跟踪控制。

4 展望

随着传感器技术和机器人技术等相关技术的发展,农业装备正向着信息化及智能化方向发展,但滑动现象阻碍了农业装备智能化。从目前的相关研究来看,农业装备行驶滑动辨识与控制的相关技术尚未成熟,理论、方法与实际应用还有一定距离。为促进农业装备行驶滑动方面的研究,综合研究进展和未来发展需求,在未来工作中需要对以下方面作进一步研究。

(1)农业装备行驶滑动力学理论模型研究

农业环境相比于其他环境,由于生物与土壤共同作用,在发生滑移时有其特有的滑动力学特性,这些特性是后续研究农业装备行驶滑动辨识与控制的前提与基础。为促进农业装备行驶滑动研究的发展,综合前文分析,建议进行以下研究:①针对目前所提出的滑动力学特性研究均局限于特定环境下,并且很难直接转化为滑动观测量的现状,研究不同农业环境中农业装备行驶滑动情况,开发建立不同农业地形条件下滑动行为模型。②针对目前研究主要聚焦于履带行驶滑动,而履带行驶滑动力学模型并不完全适用于轮式的现状,研究建立农业装备轮胎发生滑动时轮胎-地面互作关系和滑动力学理论模型。③针对目前行驶机构在高含水率土壤下的滑动情况研究较少但滑动较频繁的现状,考虑不同状态下的行驶机构和土壤,揭示行驶机构与高含水率土壤之间的滑动力学特性及滑动机理。

(2)农业装备行驶滑动实时辨识方法研究

针对农业装备行驶滑动辨识,最理想的情况是在发生滑动前进行预测,进而通过控制行驶机构来避免滑动或降低滑动导致的危害,然而由于滑动现象的随机性、时变性、突变性,该目标极难实现,因此对滑动现象更灵敏识别同时避免自身正常移动的误识别成为研究重点。综合前文分析,通过数据驱动和数学模型的方法很难对滑动现象实现实时辨识,目前的研究大多以滑动补偿为主,对于农业环境下滑动实时预测与实际应用还存在一定的差距,理论、技术和应用还有待完善。因此在完善目前滑动辨识方法的基础上,应进行农业装备滑动实时辨识及预测方法创新,可以从以下方面开展研究:①针对农业复杂环境导致的频繁颠簸及算力不足的问题,考虑不同传感器的优缺点,开发滑动辨识的新方法,实现对复杂农业环境的农业装备行驶滑动实时辨识。②随着机器学习技术的兴起,探索将深度学习等新技术新方法应用于农业装备行驶滑动辨识的研究中。

(3)农业装备行驶滑动控制方法研究

在进行农业装备滑动实时辨识及预测方法创新的基础上,需要进行与之匹配的滑动控制方法研究,使之能够真正应用于农业生产之中,最终达到减少甚至避免滑动的目的,进而促进农业智能化生产的发展,综合前文分析,建议从以下方面开展研究:①针对现有研究大多集中在小侧向加速度的常规工况,对行驶机构在大侧向加速度的极限工况和曲率不连续、路面突变等复杂工况考虑不足,算法的适用性和鲁棒性尚缺乏足够验证的现状,基于滑动辨识方法创新,针对作业环境中可能遇到的地形和工况,分别试验其滑动情况,根据滑动程度和频率,提出动力最优匹配控制策略,通过对动力的合理配置实现不同环境下的滑动控制。②针对现有研究大多针对农业环境的中低滑场景,而无法兼顾高滑场景,在发生瞬时大幅度滑动时,往往无法实现有效及时的跟踪控制的现状,在分析处于高滑状态下农业装备运动学和动力学状态的基础上,探索建立滑动控制与高滑状态的映射关系,提升高滑发生时的响应速度,进而通过动力控制对滑动实现即时补偿,达到降低滑动危害的效果。

[1] EDAN Y, HAN S, KONDO N. Automation in agriculture[M]∥NOF S Y. Automation in agriculture. Springer Berlin, Heidelberg, 2009: 1095-1128.

[2] HAN X, KIM H J, JEON C W, et al. Development of a low-cost GPS/INS integrated system for tractor automatic navigation[J]. International Journal of Agricultural and Biological Engineering, 2017, 10(2): 123-131.

[3] 关卓怀, 沐森林, 吴崇友, 等. 履带式联合收获机水田作业转向运动学分析与试验[J]. 农业工程学报, 2020, 36(13): 29-38.
GUAN Zhuohuai, MU Senlin, WU Chongyou, et al. Steering kinematic analysis and experiment of tracked combine harvester working in paddy field[J]. Transactions of the CSAE, 2020, 36(13): 29-38. (in Chinese)

[4] JO-YUNGWONG. 地面车辆原理(第4版)[M]. 贾振中, 李升波, 胡晓松,译. 北京:机械工业出版社, 2018.

[5] 胡纪滨,李雪原,魏超. 装甲车辆行驶原理[M]. 北京:北京理工大学出版社, 2020.

[6] BEKKER M G.地面-车辆系统导论[M]. 《地面-车辆系统导论》翻译组,译. 北京:机械工业出版社, 1978.

[7] WENDY W L, SHOOP S A. State of the knowledge of vegetation impact on soil strength and trafficability[J]. Journal of Terramechanics,2018,78: 1-14.

[8] WONG J. Theory of ground vehicles(4th ed)[M]. New York: Wiley, 2008.

[9] LYASKO M. Slip sinkage effect in soil-vehicle mechanics[J]. Journal of Terramechanics, 2010, 47(1):21-31.

[10] AZIMI A, KOVECSE J, ANGELES J. Wheel-soil interaction model for rover simulation and analysis using elastoplasticity theory[J]. IEEE Transactions on Robotics,2013,29(5):1271-1288.

[11] LI G B, DAI L, XU M H, et al. Track link-terrain interaction simulation based on terramechanics[J]. Key Engineering Materials, 2014, 572: 640-643.

[12] RAYMOND J, JAYAJUMAR P. The shearing edge of tracked vehicle-soil interactions in path clearing applications utilizing multi-body dynamics modeling &simulation[J]. Journal of Terramechanics, 2015, 58: 39-50.

[13] SPITERI C, AL-MILLI S, GAO Y, et al. Real-time visual sinkage detection for planetary rovers[J]. Robotics and Autonomous Systems, 2015, 72:307-317.

[14] TANG S, YUAN S, HU J, et al. Modeling of steady-state performance of skid-steering for high-speed tracked vehicles[J]. Journal of Terramechanics, 2017, 73:25-35.

[15] EDWIN P, SHANKAR K, KANNAN K. Soft soil track interaction modeling in single rigid body tracked vehicle models[J]. Journal of Terramechanics, 2018, 77:1-14.

[16] NICOLINI A, MOCERA F, SOMA A. Multibody simulation of a tracked vehicle with deformable ground contact model[J]. Proceedings of the Institution of Mechanical Engineers, 2019, 233(1): 152-162.

[17] 毕松,韩奕非.果园滑动转向机器人轮胎动力学参数实时估计方法[J]. 农业机械学报, 2023, 54(8): 110-121, 192.
BI Song, HAN Yifei. Real-time estimation method of tire dynamics parameters for sliding steering robots in orchards[J]. Transactions of the Chinese Society for Agricultural Machinery, 2023, 54(8): 110-121, 192. (in Chinese)

[18] 李军, 李强, 周靖凯, 等. 软土条件下履带-地面相互作用分析[J]. 兵工学报, 2012, 33(12): 1423-1429.
LI Jun, LI Qiang, ZHOU Jingkai, et al. Analysis of track-terrain interaction on soft soil[J]. Acta Armamentarii, 2012, 33(12): 1423-1429. (in Chinese)

[19] 迟媛, 张荣蓉,任洁, 等. 履带车辆差速转向时载荷比受土壤下陷的影响[J]. 农业工程学报, 2016, 32(17): 62-68.
CHI Yuan, ZHANG Rongrong, REN Jie, et al. Steering power ratio affected by soil sinkage with differential steering in tracked vehicle[J]. Transactions of the CSAE, 2016, 32(17): 62-68. (in Chinese)

[20] 杜永浩, 高经纬, 姜乐华. 基于离散元法的刚性履带低含水软地面附着特性数值分析[J]. 计算力学学报, 2017, 34(3): 384-389.
DU Yonghao, GAO Jingwei, JIANG Lehua. Numerical analysis on the adhesion property of rigid track on the soft ground with low moisture by discrete element method[J]. Chinese Journal of Computational Mechanics, 2017, 34(3): 384-389. (in Chinese)

[21] 孙中兴, 唐力伟, 汪伟, 等. 考虑土壤滑转流动的柔性履带应力分布研究[J]. 农业机械学报, 2017, 48(1): 317-324.
SUN Zhongxing, TANG Liwei, WANG Wei, et al. Flexible track stress distribution considering slip subsidence[J]. Transactions of the Chinese Society for Agricultural Machinery,2017,48(1):317-324. (in Chinese)

[22] 姚禹, 王博, 高智. 履带-地面耦合系统机理分析与建模[J]. 长春工业大学学报, 2018, 39(6): 14-19.
YAO Yu, WANG Bo, GAO Zhi. Mechanism analysis and modeling of track-soil coupling system[J]. Journal of Changchun University of Technology, 2018, 39(6): 14-19. (in Chinese)

[23] BALAKRISHNA R, GHOSAL A. Modeling of slip for wheeled mobile robots[J]. IEEE Transactions on Robotics and Automation, 1995, 11(1): 126-132.

[24] DING L, DENG Z, GAO H, et al. Interaction mechanics model for rigid driving wheels of planetary rovers moving on sandy terrain with consideration of multiple physical effects[J]. Journal of Field Robotics, 2015, 32(6): 827-859.

[25] SEEGMILLER N, KELLY A. Enhanced 3D kinematic modeling of wheeled mobile robots[C]∥Robotics: Science and Systems, 2014: 1002-1011.

[26] SEEGMILLER N, ROGERS-MARCOVITZ F, MILLER G, et al. Vehicle model identification by integrated prediction error minimization[J]. International Journal of Robotics Research, 2013, 32(8): 912-931.

[27] BALARAM J. Kinematic observers for articulated rovers[C]∥Proceedings IEEE International Conference on Robotics and Automation. IEEE, 2000: 2597-2604.

[28] SHILLER Z, SERATE W, HUA M. Trajectory planning of tracked vehicles[C]∥Proceedings IEEE International Conference on Robotics and Automation. IEEE, 1993: 796-801.

[29] LE A T, RYE D C, DURRANT-WHYTE H F. Estimation of track-soil interactions for autonomous tracked vehicles[C]∥Proceedings of International Conference on Robotics and Automation. IEEE, 1997: 1388-1393.

[30] IAGNEMMA K, KANG S, SHIBLY H, et al. Online terrain parameter estimation for wheeled mobile robots with application to planetary rovers[J]. IEEE Transactions on Robotics, 2004, 20(5): 921-927.

[31] SONG Z, HUTANGKABODEE S, ZWEIRI Y H, et al. Identification of soil parameters for unmanned ground vehicles track-terrain interaction dynamics[C]∥SICE 2004 Annual Conference. IEEE, 2004: 2255-2260.

[32] SCHEDING S, DISSANAYAKE G, NEBOT E M, et al. An experiment in autonomous navigation of an underground mining vehicle[J]. IEEE Transactions on Robotics and Automation, 1999, 15(1): 85-95.

[33] ZHOU B, HAN J. Nonlinear estimation methods for autonomous tracked vehicle with slip[J]. Chinese Journal of Mechanical Engineering, 2007, 20(4): 1-7.

[34] DAR T M, LONGORIA R G. Slip estimation for small-scale robotic tracked vehicles[C]∥Proceedings of the 2010 American Control Conference. IEEE, 2010: 6816-6821.

[35] CHWA D. Fuzzy adaptive tracking control of wheeled mobile robots with state-dependent kinematic and dynamic disturbances[J]. IEEE Transactions on Fuzzy Systems, 2011, 20(3): 587-593.

[36] LINDEMANN R A, VOORHEES C J. Mars exploration rover mobility assembly design, test and performance[C]∥IEEE International Conference on Systems. IEEE, 2005: 450-455.

[37] ANGELOVA A, MATTHIES L, HELMICK D M, et al. Learning and prediction of slip from visual information[J]. Journal of Field Robotics, 2010, 24(3):205-231.

[38] ANGELOVA A, MATTHIES L, HELMICK D, et al. Learning to predict slip for ground robots[C]∥Proceedings 2006 IEEE International Conference on Robotics and Automation. IEEE, 2006: 3324-3331.

[39] GONZALEZ R, APOSTOLOPOILOS D, IAGNEMMA K. Slippage and immobilization detection for planetary exploration rovers via machine learning and proprioceptive sensg[J]. Journal of Field Robotics, 2018, 35(2): 231-247.

[40] GONZALEZ R,CHANDLER S,APOSTOLOPOULOS D. Characterization of machine learning algorithms for slippage estimation in planetary exploration rovers[J]. Journal of Terramechanics, 2019, 82: 23-34.

[41] DIMASTROGIOVANNI M, CORDES F, REINA G. Terrain estimation for planetary exploration robots[J]. Applied Sciences, 2020, 10(17): 6044.

[42] ROTHROCK B, KENNEDY R, CUNNINGHAM C, et al. Spoc: deep learning-based terrain classification for mars rover missions[C]∥AIAA SPACE, 2016: 5539.

[43] CUNNINGHAM C, ONO M, NESNAS I, et al. Locally-adaptive slip prediction for planetary conference rovers using Gaussian processes[C]∥2017 IEEE International on Robotics and Automation (ICRA). IEEE, 2017: 5487-5494.

[44] SKONIECZNY K, SHUKLA D K, FARAGALLI M, et al. Data-driven mobility risk prediction for planetary rovers[J]. Journal of Field Robotics, 2019, 36(2): 475-491.

[45] KOV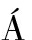

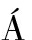CS L L, GHOTBI B, GONZ width=11,height=14,dpi=110

LEZ F, et al. Effect of gravity in wheel/terrain interaction models[J]. Journal of Field Robotics, 2020, 37(5): 754-767.

[46] GONZALEZ R, IAGNEMMA K. Slippage estimation and compensation for planetary exploration rovers. State of the art and future challenges[J]. Journal of Field Robotics, 2019, 35(4): 564-577.

[47] BORENSTEIN J, EVERETT H R, FENG L. Where am I? Sensors and methods for mobile robot positioning[R]. Ann Arbor: University of Michigan, 1996: 27.

[48] GERSDORF B, FREESE U. A Kalman filter for odometry using a wheel mounted inertial sensor[C]∥The 10th International Conference on Informatics in Control, Automation and Robotics (ICINCO), 2013: 388-395.

[49] DU S. Rotary inertial navigation system with a low-cost MEMS IMU and its integration with GNSS[D]. Alberta: University of Calgary, 2015.

[50] BUSSMANN K, MEYER L, STEIDLE F, et al. Slip modeling and estimation for a planetary exploration rover: experimental results from Mt. Etna[C]∥2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2018: 2449-2456.

[51] ZWIERZCHOWSKI J, PIETRALA D, NAPIERALSK J, et al. A mobile robot position adjustment as a fusion of vision system and wheels odometry in autonomous track driving[J]. Applied Sciences, 2021, 11(10): 4496.

[52] WANG S, ZHAI J. A trajectory tracking method for wheeled mobile robots based on disturbance observer[J]. International Journal of Control, Automation and Systems, 2020, 18(8): 2165-2169.

[53] FERNANDEZ D, PRICE A. Visual odometry for an outdoor mobile robot[C]∥IEEE Conference on Robotics, Automation and Mechatronics. IEEE, 2004: 816-821.

[54] NOURANI-VATANI N, ROBERTS J, SRINIVASAN M V. Practical visual odometry for car-like vehicles[C]∥2009 IEEE International Conference on Robotics and Automation. IEEE, 2009: 3551-3557.

[55] BORENSTEIN J, EVERETT H R, FENG L, et al. Mobile robot positioning: sensors and techniques[J]. Journal of Robotic Systems, 1997, 14(4): 231-249.

[56] NOURELDIN A, KARAMAT T B, GEORGY J. Fundamentals of inertial navigation, satellite-based positioning and their integration[M]. Springer Science &Business Media, 2012.

[57] WANG D, LIANG H, ZHU H, et al. A bionic camera-based polarization navigation sensor[J]. Sensors, 2014, 14(7): 13006-13023.

[58] WOODMAN O J. An introduction to inertial navigation[R]. University of Cambridge, 2007.

[59] RONE W, BEN-TZVI P. Mapping, localization and motion planning in mobile multi-robotic systems[J]. Robotica, 2013, 31(1): 1-23.

[60] EL-RABBANY A. Introduction to GPS: the global positioning system[M]. Artech House, 2002.

[61] COOK G, ZHANG F. Mobile robots: navigation, control and sensing, surface robots and AUVs[M]. John Wiley &Sons, 2020.

[62] MAKLOUF O, ADWAIB A. Performance evaluation of GPS\INS main integration approach[J]. International Journal of Aerospace and Mechanical Engineering, 2014, 8(2): 476-484.

[63] GONZALEZ R, RODRIGUEZ F, GUZMAN J L, et al. Combined visual odometry and visual compass for off-road mobile robots localization[J]. Robotica, 2012, 30(6): 865-878.

[64] HORN J, SCHMIDT G. Continuous localization of a mobile robot based on 3D-laser-range-data, predicted sensor images, and dead-reckoning[J]. Robotics and Autonomous Systems, 1995, 14(2-3): 99-118.

[65] TAKAHASHI T. 2D localization of outdoor mobile robots using 3D laser range data[J]. Robotics Institute Carnegie Mellon University Pittsburgh, 2007, 11(7): 1-33.

[66] LINGEMANN K, NÜCHTER A, HERTZBERG J, et al. High-speed laser localization for mobile robots[J]. Robotics and Autonomous Systems, 2005, 51(4): 275-296.

[67] FRONTONI E. Vision based mobile robotics: mobile robot localization using vision sensors and active probabilistic approaches[M]. Lulu. com, 2012.

[68] CAMPBELL J, SUKTHANKAR R, NOURBAKHSH I, et al. A robust visual odometry and precipice detection system using consumer-grade monocular vision[C]∥Proceedings of the 2005 IEEE International Conference on Robotics and Automation. IEEE, 2005: 3421-3427.

[69] NAGATANI K, IKEDA A, ISHIGAMI G, et al. Development of a visual odometry system for a wheeled robot on loose soil using a telecentric camera[J]. Advanced Robotics, 2010, 24(8-9): 1149-1167.

[70] HOWARD A. Real-time stereo visual odometry for autonomous ground vehicles[C]∥2008 IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE, 2008: 3946-3952.

[71] NISTÉR D, NARODITSKY O, BERGEN J. Visual odometry[C]∥Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. IEEE, 2004.

[72] 陈明方,黄良恩,王森,等.移动机器人视觉里程计技术研究综述[J].农业机械学报,2024,55(3):1-20.
CHEN Mingfang, HUANG Liang’en, WANG Sen, et al. Survey of research on visual odometry technology for mobile robots[J]. Transactions of the Chinese Society for Agricultural Machinery,2024,55(3):1-20.(in Chinese)

[73] KILIC C, OHI N, GU Y, et al. Slip-based autonomous ZUPT through Gaussian process to improve planetary rover localization[J]. IEEE Robotics and Automation Letters, 2021, 6(3): 4782-4789.

[74] MAIMONE M, CHENG Y, MATTHIES L. Two years of visual odometry on the mars exploration rovers[J]. Journal of Field Robotics, 2007, 24(3):169-186.

[75] DING L, GAO H, DENG Z, et al. Experimental study and analysis on driving wheels’ performance for planetary exploration rovers moving in deformable soil[J]. Journal of Terramechanics, 2011, 48:27-45.

[76] DING L, GAO H, DENG Z, et al. Slip ratio for lugged wheel of planetary rover in deformable soil: definition and estimation[C]∥2009 IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE, 2009: 3343-3348.

[77] LI N, DING L, GAO H, et al. Detection method for planet rover slip ratio based on vision measuring technology[C]∥Proceedings of the 32nd Chinese Control Conference, 2013:3673-3679.

[78] LI N, GAO H, DING L, et al. Research on feature extraction and segmentation of rover wheel imprint[J]. The Journal of Supercomputing, 2020, 76: 2357-2373.

[79] 李楠, 高海波, 吕凤天, 等. 车辙图像频域分析及星球车车轮滑转率估计方法[J]. 宇航学报, 2016, 37(11): 1356-1364.
LI Nan, GAO Haibo, LÜ Fengtian, et al. Wheel trace imprint image frequency domain analysis and rover wheel slip ratio estimation[J]. Journal of Astronautics, 2016, 37(11): 1356-1364. (in Chinese)

[80] 吕凤天, 高海波, 李楠, 等. 基于单目视觉的松软地面星球车车轮滑转率估计[J]. 机械工程学报, 2020, 56(2): 77-85.
LÜ Fengtian, GAO Haibo, LI Nan, et al. Monocular vision-based estimation of wheel slip ratio for planetary rovers in soft terrain[J]. Journal of Mechanical Engineering, 2020, 56(2): 77-85. (in Chinese)

[81] CORRADINI M L, LEO T, ORLANDO G. Robust stabilization of a mobile robot violating the nonholonomic constraint via quasi-sliding modes[C]∥Proceedings of the 1999 American Control Conference. IEEE, 1999: 3935-3939.

[82] WANG Z P, GE S S, LEE T H. Adaptive neural network control of a wheeled mobile robot violating the pure nonholonomic constraint[C]∥2004 43rd IEEE Conference on Decision and Control (CDC). IEEE, 2004: 5198-5203.

[83] WANG D, LOW C B. Modeling and analysis of skidding and slipping in wheeled mobile robots: control design perspective[J]. IEEE Transactions on Robotics, 2008, 24(3): 676-687.

[84] 熊璐, 杨兴, 卓桂荣, 等. 无人驾驶车辆的运动控制发展现状综述[J]. 机械工程学报, 2020, 56(10): 127-143.
XIONG Lu, YANG Xing, ZHUO Guirong, et al. Review on motion control of autonomous vehicles[J]. Journal of Mechanical Engineering, 2020, 56(10): 127-143. (in Chinese)

[85] 柴善鹏, 姚立健, 徐丽君, 等. 基于动态前视距离纯追踪模型的温室农机路径跟踪研究[J]. 中国农机化学报, 2021, 42(11): 58-64, 79.
CHAI Shanpeng, YAO Lijian, XU Lijun, et al. Research on greenhouse agricultural machinery path tracking based on dynamic look ahead distance pure pursuit model[J]. Journal of Chinese Agricultural Mechanization, 2021, 42(11): 58-64, 79. (in Chinese)

[86] 张文利, 郭宇, 陈开臻, 等. 基于预适应路径追踪的收割机RAC导航系统[J]. 中国农业信息, 2020, 32(1): 1-8.
ZHANG Wenli, GUO Yu, CHEN Kaizhen, et al. RAC navigation system of harvester based on pre-adaptive path tracking model[J]. China Agricultural Informatics, 2020, 32(1): 1-8. (in Chinese)

[87] WANG H, NIU W, FU W, et al. A low-cost tractor navigation system with changing speed adaptability[C]∥2021 33rd Chinese Control and Decision Conference (CCDC). IEEE, 2021: 96-102.

[88] RAFFO G V, GOMES G K, NORMEY-RICO J E, et al. A predictive controller for autonomous vehicle path tracking[J]. IEEE Transactions on Intelligent Transportation Systems, 2009, 10(1): 92-102.

[89] SONG X, SHAO Y, QU Z. A vehicle trajectory tracking method with a time-varying model based on the model predictive control[J]. IEEE Access, 2019, 8: 16573-16583.

[90] LENAIN R, THUILOT B, CARIOU C, et al. Mobile robot control in presence of sliding: application to agricultural vehicle path tracking[C]∥Proceedings of the 45th IEEE Conference on Decision and Control. IEEE, 2006: 6004-6009.

[91] 刘正铎, 张万枝, 吕钊钦, 等. 基于非线性模型的农用车路径跟踪控制器设计与试验[J]. 农业机械学报, 2018, 49(7): 23-30.
LIU Zhengduo, ZHANG Wanzhi, LÜ Zhaoqin, et al. Design and test of path tracking controller based on nonlinear model prediction[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(7): 23-30. (in Chinese)

[92] 郝思佳, 李丽霞, 付卫强, 等. 牵引式农机-机具二维三自由度运动学模型研究[J]. 中国农机化学报, 2020, 41(10): 111-117.
HAO Sijia, LI Lixia, FU Weiqiang, et al. Research on 3-DOF kinematic model of 2-D trailed agricultural machinery-machine[J]. Journal of Chinese Agricultural Mechanization, 2020, 41(10):111-117. (in Chinese)

[93] CHO S I, LEE J H. Autonomous speedsprayer using differential global positioning system, genetic algorithm and fuzzy control[J]. Journal of Agricultural Engineering Research, 2000, 76(2): 111-119.

[94] 沈跃,张亚飞,刘慧,等.农业装备自动控制技术研究综述[J].农业机械学报, 2023, 54(8): 1-18.
SHEN Yue, ZHANG Yafei, LIU Hui, et al. Research review of agricultural equipment automatic control technology[J]. Transactions of the Chinese Society for Agricultural Machinery, 2023, 54(8): 1-18. (in Chinese)

[95] 王伟康. 基于GNSS的双电机履带式水稻收获机底盘自动导航系统设计与试验[D]. 武汉: 华中农业大学, 2022.
WANG Weikang. Design and test of a GNSS-based automatic navigation system for a dual-motor crawler-type rice harvester chassis[D]. Wuhan: Huazhong Agricultural University, 2022. (in Chinese)

[96] 赵春召.基于自主导航四轮驱动液压底盘关键技术研究[D].济南: 济南大学,2022.
ZHAO Chunzhao. Research on key technology of four-wheel drive hydraulic chassis based on autonomous navigation[D]. Ji’nan: University of Jinan, 2022. (in Chinese)

[97] KAYACAN E, KAYACAN E, RAMON H, et al. Towards agrobots: identification of the yaw dynamics and trajectory tracking of an autonomous tractor[J]. Computers and Electronics in Agriculture, 2015, 115: 78-87.

[98] 吴才聪, 吴思贤, 文龙, 等. 拖拉机自动导航变曲度路径跟踪控制[J]. 农业工程学报, 2022, 38(21): 1-7.
WU Caicong, WU Sixian, WEN Long, et al. Variable curvature path tracking control for the automatic navigation of tractors[J]. Transactions of the CSAE, 2022, 38(21): 1-7. (in Chinese)

[99] 孟庆宽, 仇瑞承, 张漫, 等. 基于改进粒子群优化模糊控制的农业车辆导航系统[J]. 农业机械学报, 2015, 46(3): 29-36.
MENG Qingkuan, QIU Ruicheng, ZHANG Man, et al. Navigation system of agricultural vehicle based on fuzzy logic controller with improved particle swarm optimization algorithm[J]. Transactions of the Chinese Society for Agricultural Machinery,2015,46(3):29-36. (in Chinese)

[100] LI Y, YU J, GUO X, et al. Path tracking method of unmanned agricultural vehicle based on compound fuzzy control[C]∥2020 IEEE 9th Joint International Information Technology and Artificial Intelligence Conference (ITAIC). IEEE, 2020: 1301-1305.

[101] BELL T. Precision robotic control of agricultural vehicles on realistic farm trajectories[D]. Stanford: Stanford University,1999.

[102] 张智刚, 罗锡文, 赵祚喜, 等. 基于Kalman滤波和纯追踪模型的农业机械导航控制[J]. 农业机械学报, 2009, 40(增刊): 6-12.
ZHANG Zhigang, LUO Xiwen, ZHAO Zuoxi, et al. Trajectory tracking control method based on Kalman filter and pure pursuit model for agricultural vehicle[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(Supp.): 6-12. (in Chinese)

[103] 胡炼, 罗锡文, 张智刚, 等. 基于CAN总线的分布式插秧机导航控制系统设计[J]. 农业工程学报, 2009, 25(12):88-92.
HU Lian, LUO Xiwen, ZHANG Zhigang, et al. Design of distributed navigation control system for rice transplanters based on controller area network[J]. Transactions of the CSAE, 2009, 25(12): 88-92. (in Chinese)

[104] ZHANG S, WEN C, REN W, et al. A joint control method considering travel speed and slip for reducing energy consumption of rear wheel independent drive electric tractor in ploughing[J]. Energy, 2023, 263: 126008.

[105] WEN C K, REN W, ZHU Q Z, et al. Reducing operation emissions and improving work efficiency using a pure electric wheel drive tractor[J]. Engineering, 2024, 24(1): 95-99.

[106] 张婷.基于扰动抑制的自主农机车作业轨迹跟踪控制方法研究[D]. 秦皇岛: 燕山大学,2023.
ZHANG Ting. On operation trajectory tracking control methods of autonomous farming vehicles based on disturbance attenuation[D]. Qinhuangdao: Yanshan University, 2023. (in Chinese)

[107] 刘进一. 基于速度自适应的拖拉机自动导航控制系统研究[D]. 北京: 中国农业大学, 2017.
LIU Jinyi. Research on automatic navigation control system of tractor based on speed adaptation[D]. Beijing: China Agricultural University, 2017. (in Chinese)

[108] BACKMAN J, OKSANEN T, VISALA A. Navigation system for agricultural machines: nonlinear model predictive path tracking[J]. Computers and Electronics in Agriculture, 2012, 82: 32-43.

[109] 徐广飞, 陈美舟, 苗河泉, 等. 基于模型预测控制的农机主从跟随作业控制方法[J]. 农业机械学报, 2020, 51(增刊2): 11-20.
XU Guangfei, CHEN Meizhou, MIAO Hequan, et al. Following operation control method of farmer machinery based on model predictive control[J]. Transactions of the Chinese Society for Agricultural Machinery, 2020, 51(Supp.2): 11-20. (in Chinese)

[110] 张会琪, 林棻, 张华达. 考虑动力学约束的智能车辆路径跟踪控制研究[J]. 重庆理工大学学报(自然科学), 2018, 32(8): 58-63, 87.
ZHANG Huiqi, LIN Fen, ZHANG Huada. Research on intelligent vehicle routing control system considering dyamic constraints[J]. Journal of Chongqing University of Technology(Natural Science),2018,32(8): 58-63, 87. (in Chinese)

[111] 张万枝, 白文静, 吕钊钦, 等. 线性时变模型预测控制器提高农业车辆导航路径自动跟踪精度[J]. 农业工程学报, 2017, 33(13):104-111.
ZHANG Wanzhi, BAI Wenjing, LÜ Zhaoqin, et al. Linear time-varying model predictive controller improving precision of navigation path automatic tracking for agricultural vehicle[J]. Transactions of the CSAE, 2017, 33(13): 104-111. (in Chinese)

[112] 王子杰. 考虑驱动轮滑移的4WID高地隙喷雾机路径跟踪模型预测控制[D]. 镇江: 江苏大学, 2022.
WANG Zijie. Path tracking model predictive control for 4WID high gap sprayer considering driving wheel slip[D]. Zhenjiang: Jiangsu University, 2022. (in Chinese)