0 引言
随着自动化技术迅速发展,工业机器人因结构紧凑、性能高效被广泛地应用于工业、农业和智能制造等行业,逐渐成为各领域的中坚力量[1]。近年来,随着机器人技术快速发展,对机器人关键构件性能提出了更高的要求。工业机器人因自重和外载荷的作用,导致构件产生变形从而引起静态变形误差和动态误差[2]。又因工业机器人是多连杆串联结构,其构件产生的变形会通过连杆累加并放大到末端。因此,如何对工业机器人进行结构优化以提升其性能成为了科研热点之一[3]。针对工业机器人的结构优化,目前使用较为广泛的优化方法有:尺寸优化和形状优化[4],还有一种为给定约束条件下寻求材料最优分布形式的拓扑优化[5-10]。相比于对尺寸、形状优化,拓扑优化能够在不改变机器人部件尺寸的情况下,对其进行性能优化,最大限度地保证了机器人整体设计完整性。对于机器人结构拓扑优化,TARN等[11]对Delta机器人主动臂进行优化,在保证机器人刚度和耐用性同时,优化后主动臂总质量减小48.8%。但上述结构优化都是建立在对机器人单个零部件进行静力分析得到的,在实际运动过程中,机器人有加、减速情况,静力分析不能很好地反映机器人运动过程中实际受力情况和整体性能。随着多体动力学软件和虚拟样机技术的快速发展,越来越多的学者利用虚拟样机和多体动力学软件进行联合拓扑优化[12]。文献[13-14]以虚拟样机技术为基础,考虑机器人L臂的动态载荷变化,联合ADAMS多体动力学仿真软件,提取机器人不同工况下的载荷谱,以提高刚度和固有频率为优化目标,建立优化数学模型。郑小飞等[15]通过对爬杆机器人进行优化,在ADAMS中设置机器人极限攀爬工况,提取其动态载荷谱,以此对夹持器与T关节进行优化,优化后机器人耗能下降7.0%。在上述优化方法中,学者们都以动载荷替换静载荷作为优化约束,但上述方法建立的多体动力学仿真模型在动力学软件中表现为理想刚体模型,然而,机器人在运行过程中受到构件柔性影响。因此,越来越多的学者[16-19]进行结构优化时,将柔性体的影响考虑到优化模型中,对工业机器人进行拓扑优化时,文献[20-21]在ADAMS中建立机器人动力学模型时,考虑到连杆自身柔性,联合有限元软件,建立了机器人刚柔耦合动力学仿真模型。但对于串联机器人来说,系统中的柔性不仅有连杆柔性,更多是关节柔性[22]。梁明轩等[23]在拓扑优化模型中,考虑了柔性关节对机器人静态性能的影响,在连杆之间以扭转弹簧的形式模拟柔性关节,并对机器人进行静力分析,以此为依据进行优化,但机器人关节柔性主要体现在其对动态特性的影响,仅进行静力学分析无法全面表达其柔性。
综上所述,目前对工业机器人拓扑优化时建立的刚柔耦合动力学模型多是考虑连杆柔性,而不涉及关节柔性。本文以QJR6-1型工业串联机器人为研究对象,以变密度法(Solid isotropic material with penalization,SIMP)为基础,通过线性加权求和法建立工业机器人大臂的多目标优化函数,通过建立包含关节、连杆柔性机器人刚柔耦合动力学模型,获得机器人大臂极限工况下动态载荷谱,并提取其作为约束条件,以科学层次分析法[24]获得优化目标的权重系数。对机器人大臂进行拓扑优化,并分析和验证优化后机器人性能。
1 优化模型建立
在进行拓扑优化建模之前,需确定机器人优化构件。首先,对工业机器人结构进行分析,由于工业机器人是串联结构,柔性体运动产生的弹性会不断放大到机器人末端,造成末端振动和执行精度下降。而机器人大臂作为上接肘部、小臂和末端,下连底部和腰部的关键构件,其结构设计在很大程度上会影响机器人整体性能表现,并且,机器人大臂内部没有电机、减速器等其他设备,所以,在对其进行结构设计时可以不考虑其他因素,保留了机器人设计的完整性,节省了时间和设计成本。
1.1 大臂拓扑优化模型建立
以变密度法(SIMP)为基础,以降低大臂柔度和提升低阶固有频率为优化目标,以应力条件、多工况载荷和体积分数为边界约束条件,最终得到机器人大臂多目标拓扑优化函数模型为
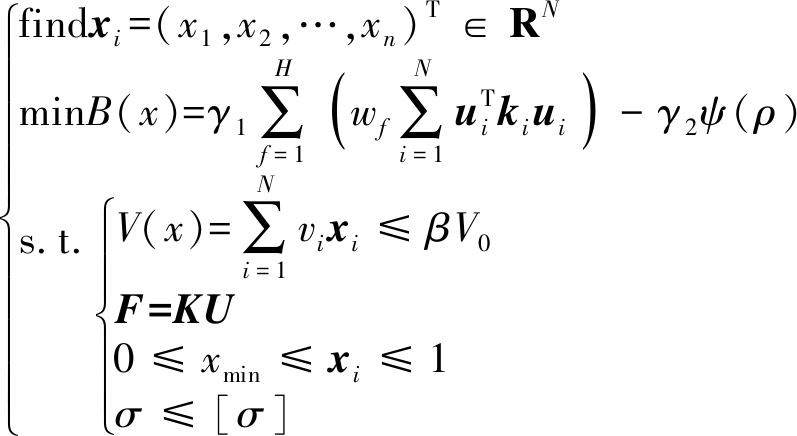
(1)
式中 xi——优化单元变量
N——优化单元个数
B(x)——优化目标函数
ui——优化单元变形量
ki——优化单元刚度矩阵
γ1——柔度权重系数
γ2——固有频率权重系数
ψ(ρ)——优化结构固有频率
H——总工况数
wf——工况f权重系数
V(x)——优化结构面积函数
vi——优化单元i体积
V0——优化区域总面积
β——体积约束分数
F——外载荷矢量
K——优化结构刚度矩阵
U——优化结构受力变形矢量
xmin——优化单元最小下限
σ——优化后结构最大应力
[σ]——材料许用应力
1.2 优化目标中权重系数确定方法
为了对多目标拓扑优化模型进行求解,需要确定各子目标权重系数,利用层次分析法确定拓扑优化模型中的权重系数,层次分析法的核心是通过对子目标两两对比得到其重要性比值,获得配对比较矩阵A,子目标之间重要性比值如表1所示。
表1 配对比较矩阵子目标之间重要性比值
Tab.1 Ratio of importance between sub-objectives of pairwise comparison matrix

重要性程度重要性比值aiji与j同重要1i比j稍重要3i比j重要5i与j稍不重要1/3i比j不重要1/5i比j很不重要1/7
两子目标之间重要性比值aij为
(2)
式中 ωi——子目标i的重要性
ωj——子目标j的重要性
在获得各子目标的重要性比值后,形成配对比较矩阵A1,即

(3)
每个配对比较矩阵都可以导出其一致性比值CR,其可以判断配对比较矩阵的一致性程度,计算式为
(4)
其中![]()
(5)
式中 CI——一致性指标
RI——随机一致性指标
λmax——配对比较矩阵A的最大特征值
n——目标数
当CR<0.1时,可以认为配对比较矩阵的不一致程度在可接受范围内,通过一致性检验。
2 机器人刚柔耦合动力学建模
2.1 柔性关节动力学描述
机器人关节变形主要由传动装置所引起,机器人关节柔性主要表现为:由于关节刚度不足,导致各个关节输入转角和输出转角在运动时会产生转角误差,并随着工业机器人多关节串联结构被放大,使机器人末端在运动时产生振动。为了表征机器人关节柔性,利用SPONG[25]提出的转子-扭簧模型建立机器人柔性关节,图1为工业机器人结构和柔性关节示意图。
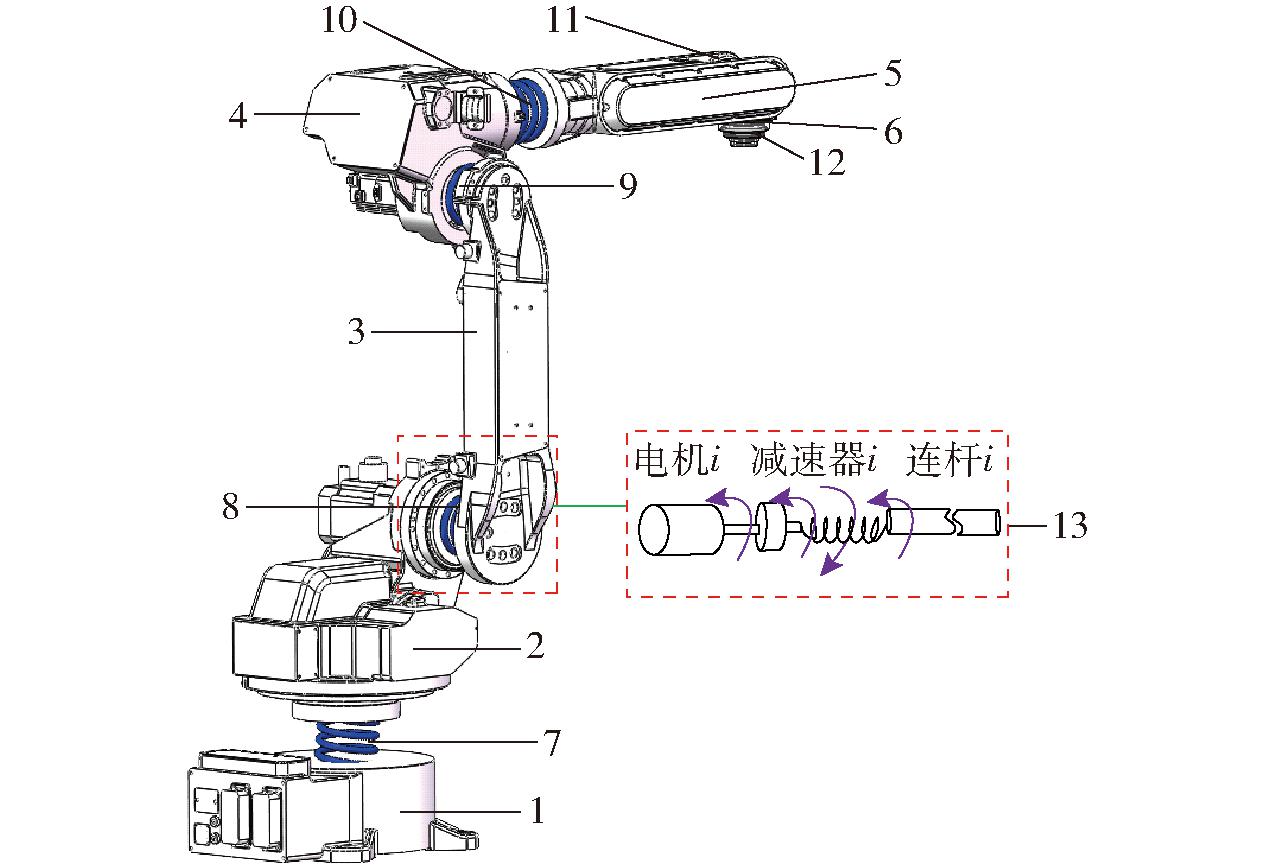
图1 机器人结构和柔性关节模型
Fig.1 Robot structure and flexible joints model
1.底部 2.腰部 3.大臂 4.肘部 5.小臂 6.末端法兰 7.关节1 8.关节2 9.关节3 10.关节4 11.关节5 12.关节6 13.柔性关节模型
机器人连杆i由扭簧产生的柔性关节力矩进行驱动,柔性关节力矩τi表达式为
τi=kiδi=ki(θri-qi)
(6)
式中 ki——关节扭转刚度
δi——减速器与连杆之间的转角误差
θri——减速器i转角 qi——连杆i转角
2.2 柔性连杆动力学描述
对于柔性体Bi来说,为了描述其柔性变形,通过有限元法将柔性体离散为有限的单元节点,如柔性体Bi上任一节点p的位置坐标描述如图2所示。图中,Ci为柔性体Bi与其他柔性体连接时产生的弹性变形,er为基坐标系,eb为点p在柔性体上的动坐标系,rop为未变形时点p在基坐标系下向量,Sio为点p在没有受到变形时动坐标系下的位置矢量,Uip为点p在动坐标上的相对变形矢量,Sip为点p在动坐标系下受到柔性体影响后的动坐标向量,由未变形的基坐标向量rop和动坐标系下变形坐标向量Sip组合形成点p在基坐标系下的坐标向量rip。
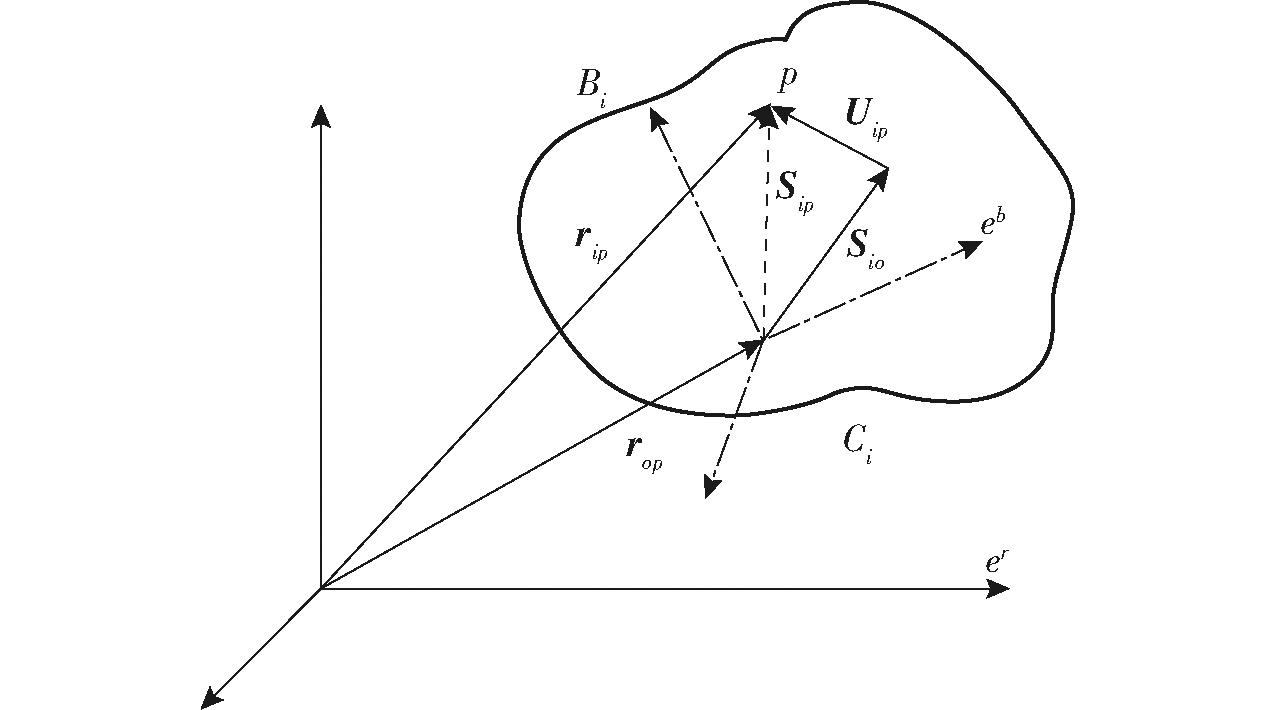
图2 柔性体节点p的坐标描述
Fig.2 Coordinate description of flexible body node p
通过假设模态法表征柔性连杆在动坐标系下的变形矢量,由此得出,柔性连杆位置坐标由X=(x,y,z)T表示,姿态则通过欧拉角e=(φ,θ,ψ)T来表征,其中,φ为进动角,θ为章动角,ψ为自转角;模态坐标为η=(η1, η2,…, ηm)T(m为模态坐标数),表示第i阶模态振幅在系统中的振型分量。综上,柔性连杆广义坐标ξ为
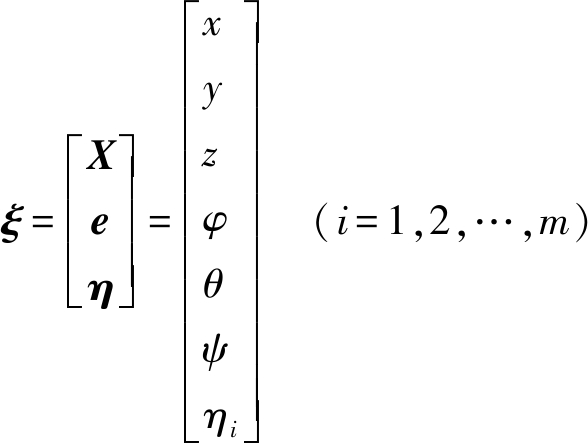
(7)
柔性连杆上第i个节点的空间坐标矢量为
(8)
式中 A——局部坐标系原点相对于惯量坐标系原点方向余弦的坐标矩阵
Si——第i个节点变形前在局部坐标系下的位置矢量
φi——第i个节点移动自由度模态矩阵子块
对式(8)进行求导,得到第i个节点速度为
(9)
式中 I——单位矩阵
![]() 向量矩阵Si所对应的对称矩阵
向量矩阵Si所对应的对称矩阵
B——欧拉角求一阶导后的速度转换矩阵
![]() 柔性连杆广义坐标进行求导后得到的速度广义矩阵
柔性连杆广义坐标进行求导后得到的速度广义矩阵
综上分析,已知某柔性连杆i上任意质点的速度矢量,可得其质点动能![]() 为
为
(10)
对式(10)积分可得柔性连杆i动能TFi为
(11)
式中 mi——第i个节点质量
Mi——柔性连杆i质量矩阵
同样地,对于刚性连杆来说,假设某刚性连杆j上任一点在基坐标系下坐标为
0rp=0Tjjrp
(12)
式中 0rp——连杆j任一点在基坐标系的坐标向量
jrp——连杆j任一点在局部坐标系中的坐标向量
0Tj——连杆j任一点从基坐标系到局部坐标系的坐标变换矩阵
则任意一点速度平方数为
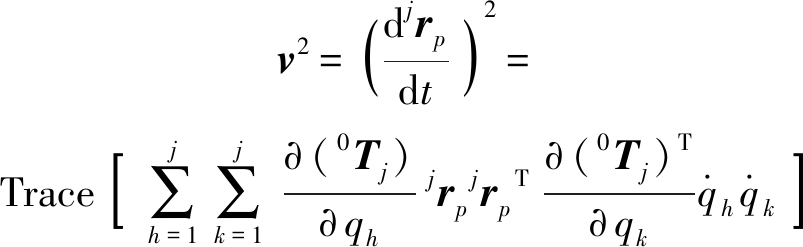
(13)
假设在刚性连杆j上的任一点质量为dm的微元动能dTRj为
![]()
![]()
![]()
(14)
综上,对其积分可得刚性连杆j动能TRj为
TRj=![]()
(15)
2.3 机器人刚柔耦合动力学建模
机器人整个刚柔耦合系统中势能分别为柔性连杆i和刚性连杆j自重产生的势能Pij、柔性连杆i由于运动过程中变形引起的弹性势能Kli、关节i产生的关节扭转势能Pki,动能为柔性连杆i和刚性连杆j产生的动能Tij。计算式为
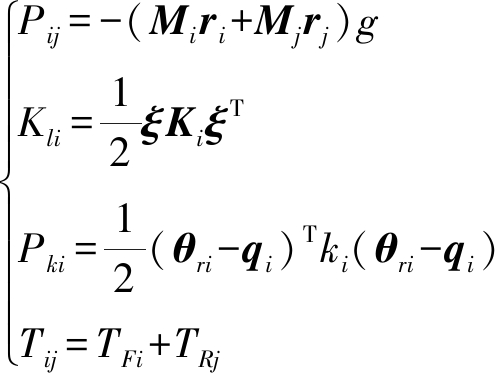
(16)
式中 Mj——刚性连杆j质量矩阵
Ki——柔性连杆i模态刚度矩阵
ri——在基坐标系下柔性连杆i质心位置坐标
rj——在基坐标系下刚性连杆j质心位置坐标
由系统中动能与势能的关系得到拉格朗日函数为
(17)
对拉格朗日函数求导得到
(18)
式中 q——广义位置矢量
![]() 广义速度矢量
广义速度矢量
Q——3n×1的广义力矩矢量
对拉格朗日方程进行整合,可得到机器人刚柔耦合动力学方程一般表达式为
(19)
式中 M(q)——质量矩阵
![]() 哥氏力以及离心力矩阵
哥氏力以及离心力矩阵
G(q)——重力项矩阵
![]() 广义加速度矢量
广义加速度矢量
3 机器人刚柔耦合动力学模型仿真
3.1 关节柔性化处理
机器人柔性关节为扭簧模型,在ADAMS软件中需要加入一个零质量的du mmy part充当桥梁,通过定义力矩函数的方式间接实现关节柔性化,图3为机器人腰部和大臂之间柔性关节驱动及力矩设置。
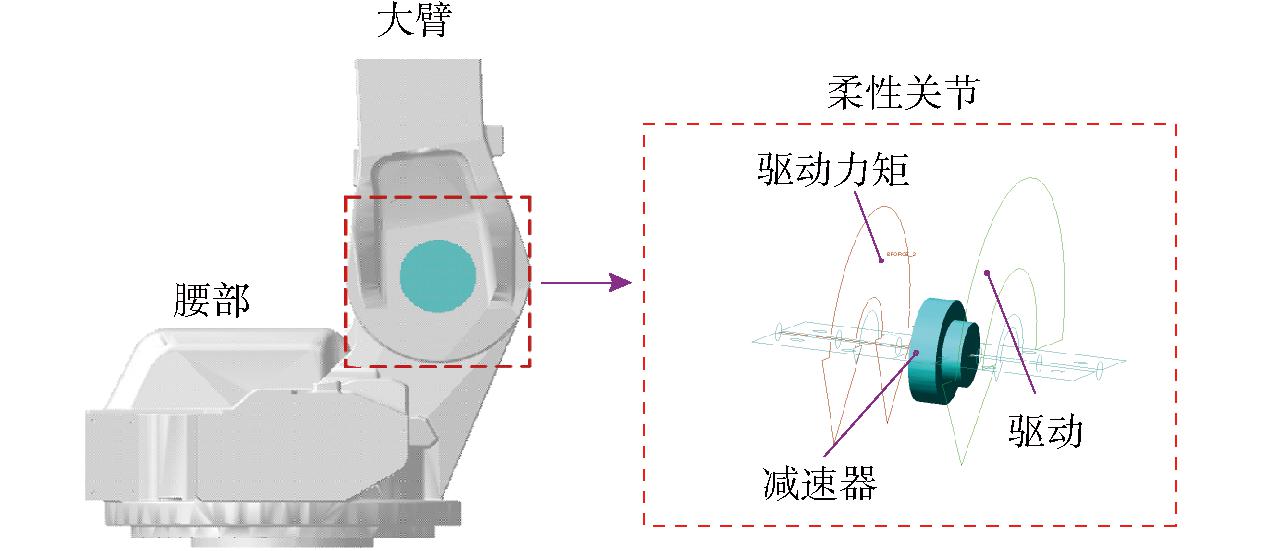
图3 机器人柔性关节驱动及力矩设置
Fig.3 Robot flexible joint driving and torque setting
3.2 连杆柔性化处理
对机器人连杆进行分析,大臂和小臂可以视为细长连杆,其自身变形是机器人连杆柔性产生的主要部分;而机器人肘部作为连接大臂和小臂的关键连杆,受到小臂和末端自重和负载的影响,其弹性变形不可忽略;机器人末端作为直接影响机器人运动轨迹精度和定位精度的连杆,为使机器人运动更真实,末端在运动过程中产生的弹性变形也需考虑进去,图4为机器人刚、柔性连杆示意图。
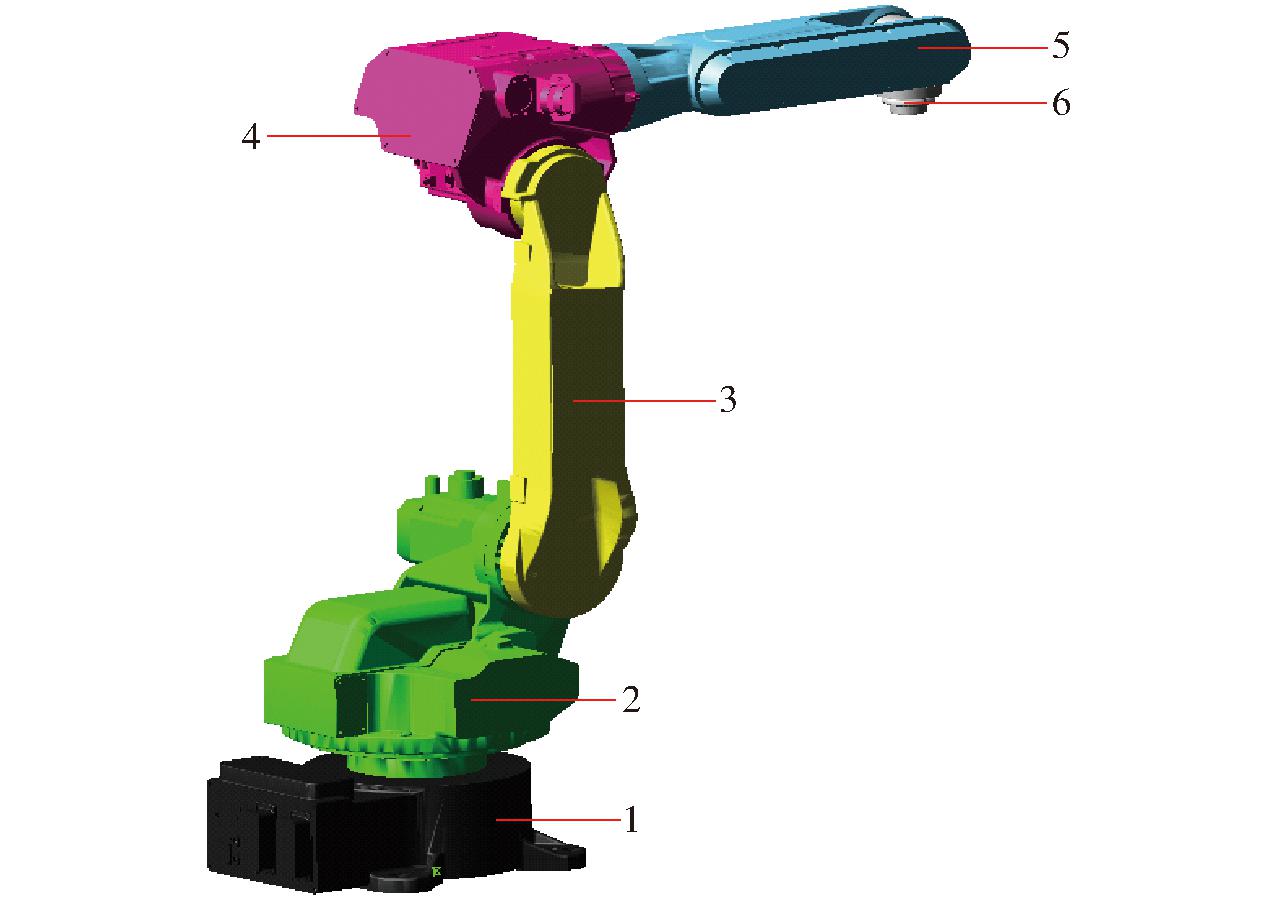
图4 机器人柔性和刚性连杆示意图
Fig.4 Schematic of robot’s flexible and rigid connecting rods
1.底部(刚性) 2.腰部(刚性) 3.大臂(柔性) 4.肘部(柔性) 5.小臂(柔性) 6.末端法兰(柔性)
将连杆模型导入有限元仿真软件ABAQUS中进行柔性化处理,生成后缀为.mnf的柔性体文件,将文件导入到ADAMS中,生成柔性连杆模型。以大臂为例,图5为柔性化后大臂1~6阶模态和所有柔性连杆装配在一起后的云图。
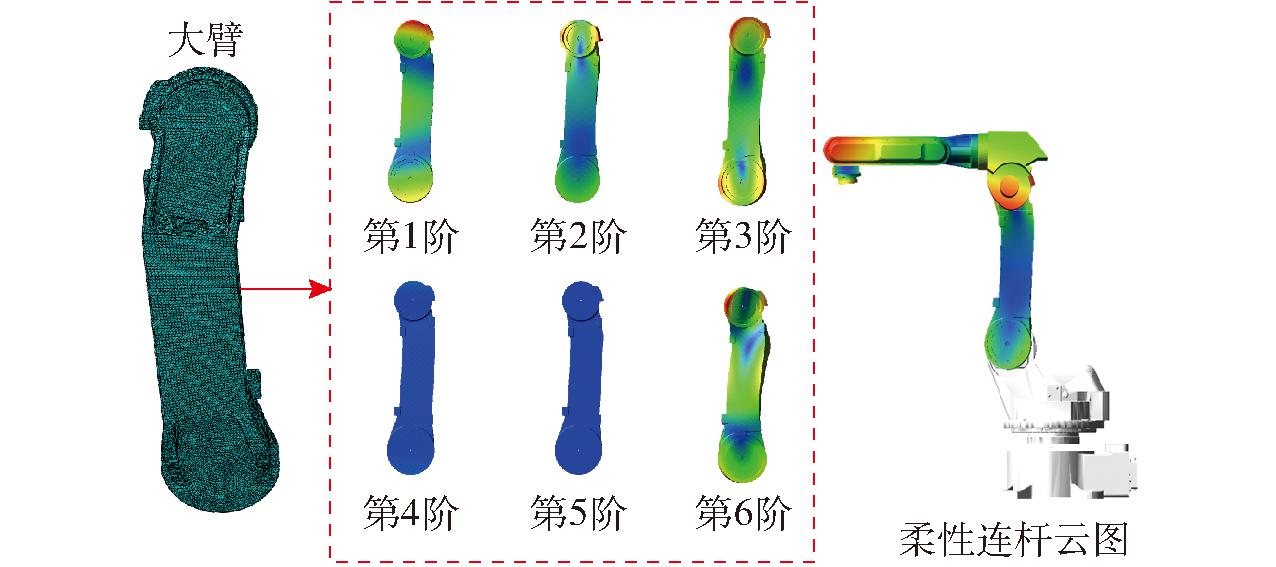
图5 大臂1~6阶模态与机器人柔性连杆云图
Fig.5 The 1st~6th order modes of forearm and robot flexible rods cloud diagram
3.3 机器人刚柔耦合动力学仿真
在多体动力学软件ADAMS中建立刚柔耦合动力学仿真模型。对于细长轻质连杆而言,当主要载荷作用于轴线垂直方向时,其变形量最大,在机器人末端施加最大负载,并调节后续连杆与大臂成为一条直线。
机器人作业时关节2和关节3的连线方向有无数个,而且大臂截面较复杂,很难判断大臂变形量最大时的载荷方向。但通过分析机器人各个关节旋转方向可知,大臂受力方向主要是由关节1、2组合运动方向决定。所以,为提取大臂所受极限载荷,将大臂上所受载荷分解为关节1、2旋转方向上的载荷。机器人前2个关节驱动参数如表2所示。
表2 关节运行参数
Tab.2 Joint operating parameters
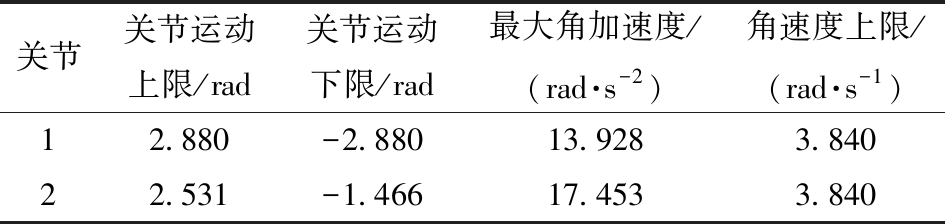
关节关节运动上限/rad关节运动下限/rad最大角加速度/(rad·s-2)角速度上限/(rad·s-1)12.880-2.88013.9283.84022.531-1.46617.4533.840
设置3个工况为:①工况1:只转动关节1,在关节1限制范围内运动,加速度100%,运行速度为最大速度。 ②工况2:只转动关节2,在关节2限制范围内运动,加速度100%,运行速度为最大速度。 ③工况3:关节1、2同时旋转,关节运动范围分别为工况1、2的各关节运动限制范围,加速度100%,运行速度为最大速度。通过ADAMS进行动力学仿真模拟各工况,为保证机器人大臂能够遍历所有可能的位置,运行时间设定为3 s,步长1 000步,提取大臂各工况下载荷谱作为边界约束条件。
4 机器人大臂拓扑优化
4.1 优化函数中权重因子分配
对于机器人大臂优化模型来说,首先考虑柔度和固有频率这两个优化目标的权重γ1、γ2,这两个目标权重可以根据其重要性给定,在大臂优化模型中,柔度重要性高于其固有频率重要性,所以,给定γ1=0.8,γ2=0.2。参考表1,对各个工况的重要程度进行对比,得到关于工况配对比较矩阵A为
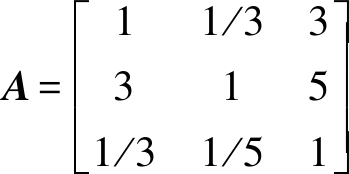
(20)
通过求解,配对比较矩阵A最大特征值λmax=3.038 5,通过式(4)可以求解得到该矩阵的一致性比值CR为0.033,小于0.1,由此可以得出矩阵一致性满足要求,对最大特征值对应的特征向量进行归一化处理,3个工况权重为α=(0.26,0.64,0.10)。同样的,对于大臂固有频率优化来说,选择低阶固有频率作为优化目标,取k=3,得到其权重为:w1=0.67, w2=0.24,w3=0.09。
4.2 大臂拓扑优化求解
在软件中设置相应权重系数,并给定相应的优化区域和非优化区域,如图6所示。
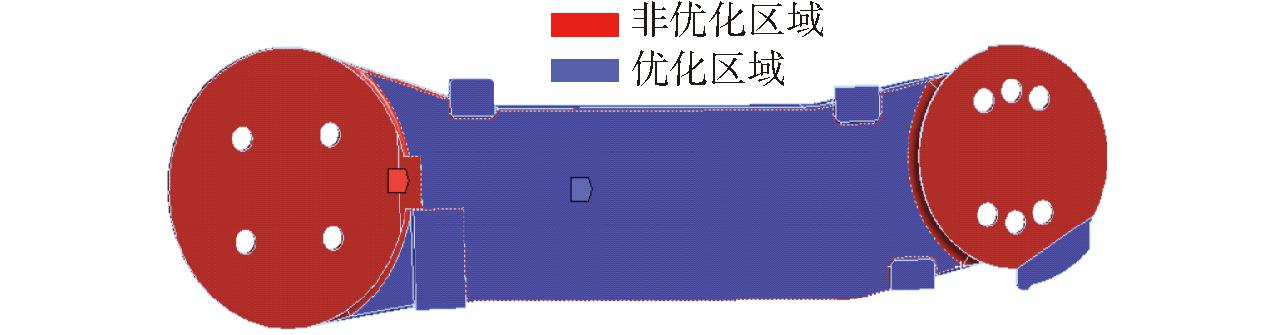
图6 优化与非优化区域
Fig.6 Optimized and non-optimized areas
在优化模型中涉及到多个工况下的载荷,利用命令流中的LSWRTIE命令将载荷写入优化软件,设置体积约束系数β为60%,求解器最大迭代次数为500,为防止刚度矩阵奇异,最小相对密度设定为0.001,计算精度为0.01%。图7a为机器人大臂拓扑优化云图,可以看出优化后的模型连续性较好,边界清晰,并且在优化模型中没有出现棋盘现象[26],并在大臂上部出现加强筋,质量从20.233 kg降至16.447 kg,下降18.71%,图7b为机器人大臂重构后模型。
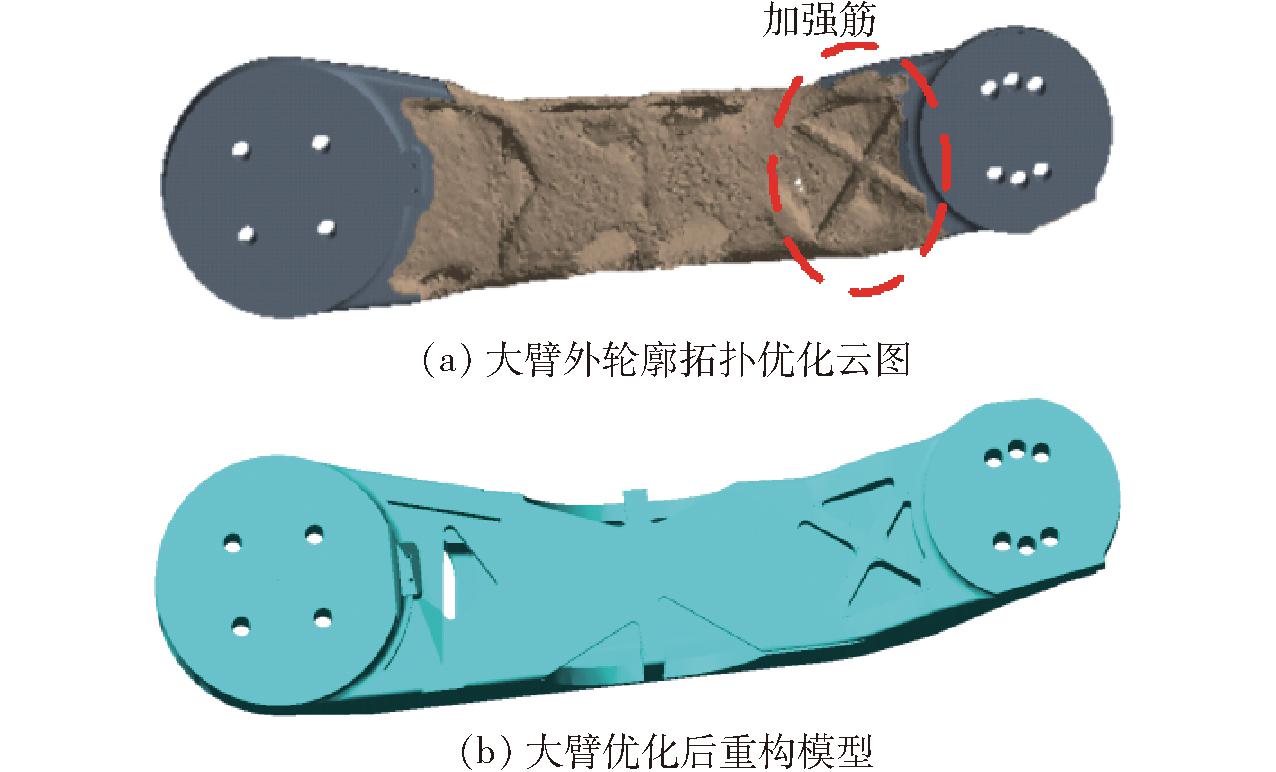
图7 大臂拓扑优化结果与模型重构
Fig.7 Forearm topology optimization result and model reconstruction
5 优化结果
5.1 静态性能对比
将优化后机器人大臂在三维建模软件中进行重构。然后,对比大臂在工况3最大载荷作用下的变形,二者变形量对比如图8所示。大臂最大变形量从0.181 mm降至0.149 mm,变形量降低17.68%。
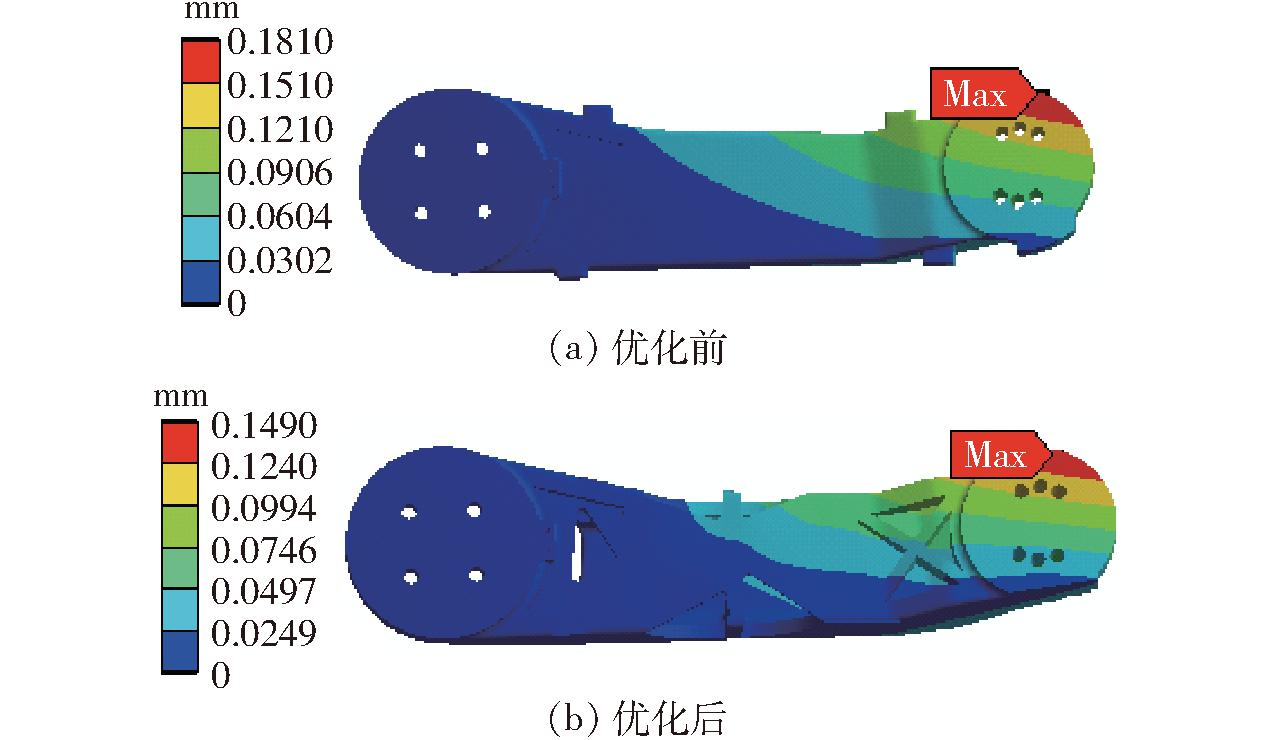
图8 大臂最大变形量对比
Fig.8 Comparison of maximum deformation displacement
机器人大臂材料为硬铝合金,密度为2 770 kg/m3,弹性模量为70 GPa,泊松比为0.33,许用应力为155 MPa,从图9可知,机器人大臂优化后最大应力为30.434 MPa,满足约束条件和优化要求。

图9 大臂优化后最大应力
Fig.9 Maximum stress after optimization of forearm
为分析优化后大臂对机器人整体性能的影响,在虚拟样机中装配好重构后的机器人模型。依据该型工业机器人最大负载许可,在末端添加垂直向下载荷58.8 N,为了更加接近柔性关节模型,以Joint连接方式取代原先的Bond约束,同时用Torsional Stiffness添加关节刚度模拟机器人柔性关节。由图10可得,优化后机器人最大变形量从0.208 mm降至0.188 mm,静态变形误差减小9.62%。

图10 优化前后机器人最大变形量对比
Fig.10 Comparison of maximum deformation displacement of robot before and after optimization
5.2 动态性能
5.2.1 大臂固有频率
提取大臂优化后前3阶固有频率,由图11可以看出,机器人大臂固有频率均有不同程度的提高,并且没有出现频率振荡现象。
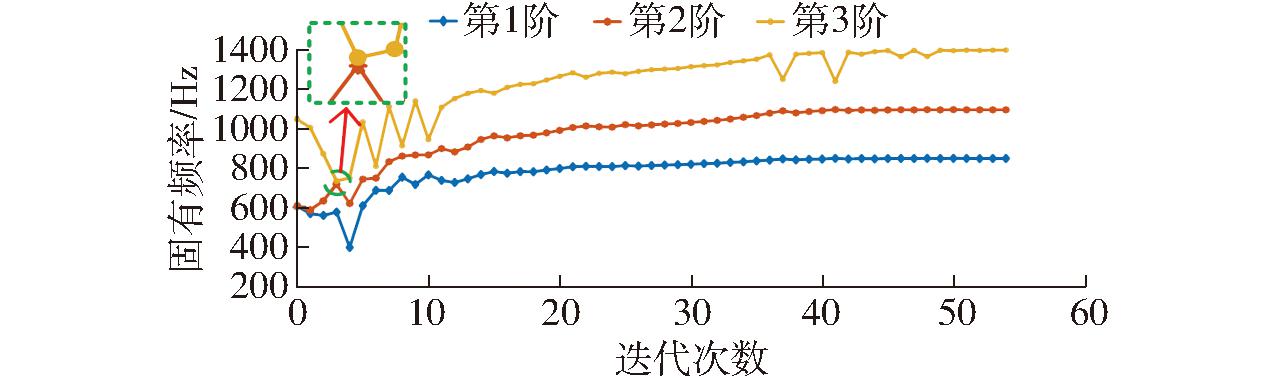
图11 大臂固有频率优化
Fig.11 Forearm natural frequencies optimization
5.2.2 末端定位精度
为分析优化后大臂对机器人动力学特性的影响,设定一段机器人末端直线运动轨迹,末端中心点从机器人基坐标系(848.5,0,1 051.5)mm匀速运动到(848.5,0,951.5)mm,轨迹长度为100 mm,根据国标GB/T 12642—2013《工业机器人 性能规范及其试验方法》中轨迹特性试验速度选10 mm/s,提取机器人末端中心点轨迹,轨迹如图12所示,刚性机器人末端不会产生振动,轨迹为一条直线。但是机器人在实际作业中,由于受到负载、关节和连杆柔性等复杂因素影响,会使机器人末端在作业时产生非线性振动,最终导致机器人在作业时产生轨迹误差和定位误差。
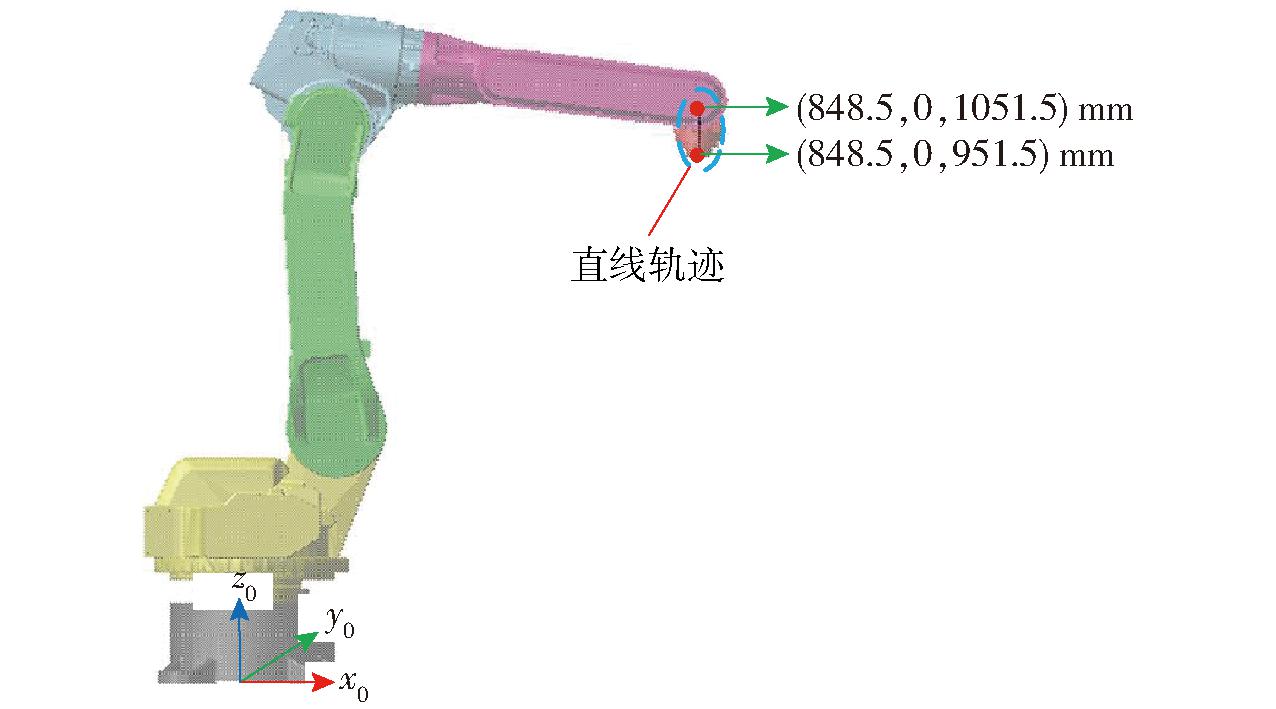
图12 直线轨迹
Fig.12 Linear trajectory
在ADAMS中对优化前机器人刚柔耦合动力学仿真模型进行装配,设置与刚体模型同样的工况,提取其末端中心点轨迹误差。在工业机器人实验平台上设置相同工况,通过上位机和激光跟踪仪采集机器人末端轨迹,图13为现场实验设备图。

图13 现场实验设备
Fig.13 Experimental devices
1.测量靶球 2.上位机 3.QJR6-1型机器人 4.激光跟踪仪
将末端中心点轨迹在基坐标系下进行表达,得到3个方向上实际的末端中心点轨迹误差,仿真轨迹误差与实验轨迹误差对比如图14所示。

图14 仿真与实验轨迹误差对比
Fig.14 Comparison of simulation and experimental trajectory errors
由图14可知,机器人轨迹误差在y轴方向上最大,实验轨迹误差和仿真轨迹误差在幅值范围和变化趋势上都比较吻合。因为实际的工业机器人是复杂的高非线性系统,所以,在误差允许范围内,刚柔耦合动力学仿真模型结果可以表征实际机器人末端在运行过程中产生的轨迹误差。在ADAMS中建立机器人优化后刚柔耦合动力学仿真模型,提取其末端轨迹误差,并与优化前轨迹误差进行对比,二者对比结果如图15所示。

图15 优化前后仿真轨迹误差对比
Fig.15 Comparison of simulation trajectory errors before and after optimization
如图15所示,大臂优化之后,机器人末端轨迹误差在3个方向上都有所减小,机器人轨迹精度得到提高。以理想终点位置为圆心,以定位误差为半径,得到定位误差圆,如图16所示,定位误差由优化前0.777 mm降至优化后0.687 mm,降低11.58%,定位精度得到提高。
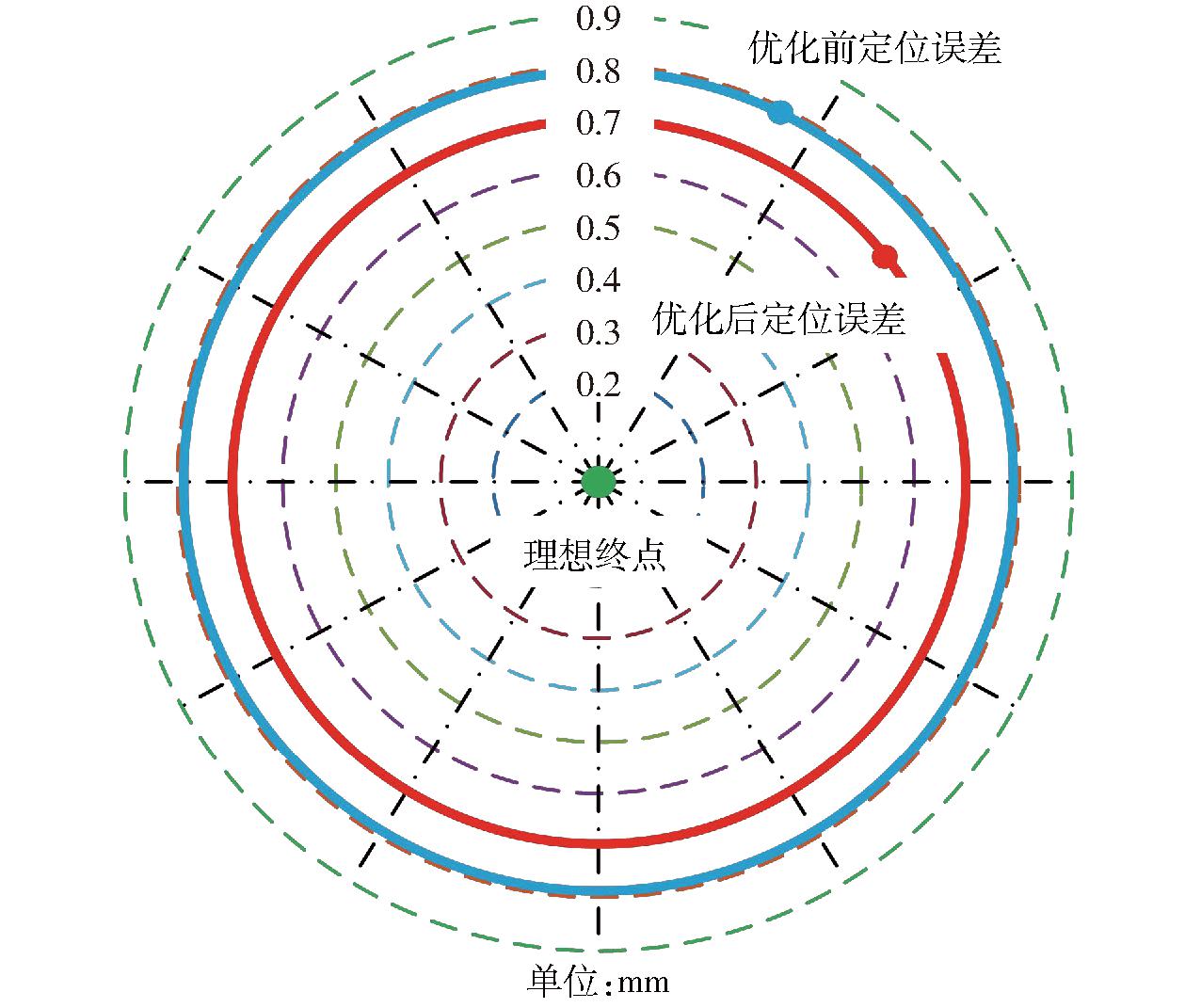
图16 定位误差对比
Fig.16 Positioning error comparison
6 结论
(1)机器人大臂优化过程中,考虑了实际运行过程中关节和连杆柔性对机器人的影响,利用假设模态法对连杆柔性状态进行表征,以扭簧模型对关节柔性进行阐述;利用ADAMS多体动力学软件建立刚柔耦合动力学模型,并与实际工况下机器人末端轨迹误差进行对比,预测了末端振动响应,精确表征了机器人动态性能。
(2)优化后机器人大臂低阶固有频率和刚度都得到提升,在工况3最大载荷作用下,大臂最大变形量从0.181 mm降至0.149 mm,变形量降低17.68%,并且优化后大臂最大应力为30.434 MPa,满足优化约束条件,表明优化结果良好。
(3)对优化后机器人整体进行分析,在末端最大负载58.8 N作用下,机器人初始静态位置最大变形量从0.208 mm降至0.188 mm,静态变形误差减小9.62%;动态定位误差从0.777 mm降低至优化后的0.687 mm,降低11.58%。机器人定位精度得到提升。
(4)对工业机器人关键构件大臂建立多目标优化函数模型,对其进行拓扑优化设计,优化后大臂在满足轻量化的同时,保证了性能要求,并提升了机器人整机静动态性能,为工业机器人本体其它构件优化提供了理论参考。
[1] 王天然. 机器人技术的发展[J]. 机器人, 2017, 39(4): 385-386.WANG Tianran. Development of robotics[J]. Robotics, 2017, 39(4): 385-386.(in Chinese)
[2] SICILIANO B, KHATIB O. Springer handbook of robotics[M]. New York: Springer Handbook of Robotics, 2008.
[3] 杨文. 工业机器人结构设计与性能提升过程中的关键问题分析[J]. 内燃机与配件, 2021(10): 78-79.YANG Wen. Analysis of key issues in the process of structural design and performance improvement of industrial robots[J]. Internal Combustion Engines and Accessories, 2021(10): 78-79.(in Chinese)
[4] 孟齐志, 谢福贵, 张赛, 等. 高速高加速并联机器人构型与尺度参数设计[J]. 机械工程学报, 2022, 58(13): 36-49.MENG Qizhi, XIE Fugui, ZHANG Sai, et al. Design of configuration and scale parameters for high-speed and high-acceleration parallel robots[J]. Journal of Mechanical Engineering, 2022, 58(13): 36-49.(in Chinese)
[5] 谢斌, 温昌凯, 杨子涵, 等. 基于实测载荷的蔬菜田间动力机械车架结构优化[J]. 农业机械学报, 2018, 49(增刊): 463-469.XIE Bin, WEN Changkai, YANG Zihan, et al. Structural optimization of vegetable field power machinery frame based on measured load[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(Supp.): 463-469.(in Chinese)
[6] 王昱, 牟剑, 曾志雄, 等. 猪舍废气净化系统填料结构多目标拓扑优化设计与试验[J]. 农业机械学报, 2021, 52(7): 329-334.WANG Yu, MOU Jian, ZENG Zhixiong. Multi-objective topology optimization design and test of pig house exhaust gas purification system packing structure[J]. Transactions of the Chinese Society for Agricultural Machinery, 2021, 52(7): 329-334.(in Chinese)
[7] KOBER M, KÜHHORN A, RADEMANN J R, et al. Nonlinear topology optimization of centrifugally loaded aero-engine part with newly developed optimality-criteria based algorithm[J].Aerospace Science &Technology, 2014, 39:705-711.
[8] BARBIERI S G, GIACOPINI M, MANGERUGA V, et al. A design strategy based on topology optimization techniques for an additive manufactured high performance engine piston[J].Procedia Manufacturing, 2017, 11:641-649.
[9] MERULLA A, GATTO A, BASSOLI E, et al. Weight reduction by topology optimization of an engine subframe mount, designed for additive manufacturing production[J].Materials Today: Proceedings, 2019, 19:1014-1018.
[10] WU Y H, LIU X M, WANG F. Topology optimization design of the bracket of a special vehicle based on FEA method[C]∥2010 Second International Conference on Computational Intelligence and Natural Computing.IEEE, 2010.
[11] TRAN T H T, NGUYEN D S, VO N T, et al. Design of delta robot arm based on topology optimization and generative design method[C]∥2020 5th International Conference on Green Technology and Sustainable Development (GTSD),2020.
[12] 张志飞, 陈仁, 徐中明, 等. 面向多目标的汽车悬架控制臂拓扑优化研究[J]. 机械工程学报, 2017, 53(4): 114-121.ZHANG Zhifei, CHEN Ren, XU Zhongming, et al. Multi-objective oriented topology optimization study of automotive suspension control arm[J]. Journal of Mechanical Engineering, 2017, 53(4): 114-121.(in Chinese)
[13] 胡启国, 胡艳敏. 工业机器人臂部静动态多目标拓扑优化[J]. 重庆交通大学学报(自然科学版), 2020, 39(9): 146-152.HU Qiguo, HU Yanmin. Static-dynamic multi-objective topology optimization of industrial robot arm[J]. Journal of Chongqing Jiaotong University (Natural Science Edition), 2020, 39(9): 146-152.(in Chinese)
[14] 王春华, 安达, 赵东辉. 工业机器人臂部静动态多目标拓扑优化设计研究[J]. 机械科学与技术, 2016, 35(2): 241-246.WANG Chunhua, AN Da, ZHAO Donghui. Research on static-dynamic multi-objective topology optimization design of industrial robot arm[J]. Mechanical Science and Technology, 2016, 35(2): 241-246.(in Chinese)
[15] 郑小飞, 黄镇海, 马小龙, 等. 基于SIMP方法的爬杆机器人结构优化与分析[J]. 工程设计学报, 2023,30(3):342-352.ZHENG Xiaofei, HUANG Zhenhai, MA Xiaolong, et al. Structural optimization and analysis of pole-climbing robot based on SIMP method[J]. Journal of Engineering Design, 2023,30(3):342-352.(in Chinese)
[16] 王家忠, 张建宝, 弋景刚. 刚柔混联的草莓采摘机械手结构设计与动力学分析[J]. 计算机集成制造系统, 2018, 24(2): 419-426.WANG Jiazhong, ZHANG Jianbao, YI Jinggang. Structural design and dynamic analysis of strawberry picking manipulator with rigid-flexible hybrid connection[J]. Computer Integrated Manufacturing Systems, 2018, 24(2): 419-426.(in Chinese)
[17] 袁铭鸿, 万安平, 童水光. 强夯机多体系统刚柔耦合动力学仿真与结构优化[J]. 科学技术与工程, 2020, 20(22): 9176-9182.YUAN Minghong, WAN Anping, TONG Shuiguang. Structural optimization and simulation of rigid-flexible coupling dynamics in multi-body system of rammer[J]. Science, Technology and Engineering, 2020, 20(22): 9176-9182.(in Chinese)
[18] 周凯红, 张学谦, 郭玉田. 基于ADAMS和ANSYS的空间四杆引纬机构优化研究[J]. 机电工程, 2021, 38(3): 383-387.ZHOU Kaihong, ZHANG Xueqian, GUO Yutian. Optimization study of spatial four-bar weft-guiding mechanism based on ADAMS and ANSYS[J]. Electromechanical Engineering, 2021, 38(3): 383-387.(in Chinese)
[19] 葛悦, 王洪波, 龚旻, 等. 火箭卫星舱壳体分离灵敏度分析与优化设计[J]. 兵器装备工程学报, 2020, 41(12): 46-52,72.GE Yue, WANG Hongbo, GONG Min, et al. Separation sensitivity analysis and optimization design of rocket satellite module shell[J]. Journal of Weapons and Equipment Engineering, 2020, 41(12): 46-52,72.(in Chinese)
[20] HUANG H B, ZHANG G. The topology optimization for L-shape arm of motorman-HP20 robot[J].Applied Mechanics and Materials, 2012, 201-202:871-874.
[21] 胡启国, 周松. 考虑刚柔耦合的工业机器人多目标可靠性拓扑优化[J]. 计算机集成制造系统, 2020, 26(3): 623-631.HU Qiguo, ZHOU Song. Multi-objective reliability topology optimization for industrial robots considering rigid-flexible coupling[J]. Computer Integrated Manufacturing Systems, 2020, 26(3): 623-631.(in Chinese)
[22] 王斌锐,方水光,金英连.综合关节和杆件柔性的机械臂刚柔耦合建模与仿真[J].农业机械学报,2012,43(2):211-215,225. WANG Binrui, FANG Shuiguang, JIN Yinglian. Modeling and simulation of rigid-flexible coupling of robotic arm with integrated joint and rod flexibility[J]. Transactions of the Chinese Society for Agricultural Machinery,2012,43(2):211-215,225.(in Chinese)
[23] 梁明轩, 李正刚, 唐任仲, 等. 基于柔性多体动力学的机械臂结构优化设计[J]. 中国机械工程, 2017, 28(21): 2562-2566.LIANG Mingxuan, LI Zhenggang, TANG Renzhong, et al. Optimized design of robotic arm structure based on flexible multibody dynamics[J]. China Mechanical Engineering, 2017, 28(21): 2562-2566.(in Chinese)
[24] 李风, 付开进, 于向军. 基于层次分析法的大型半自磨机磨矿性能优化[J]. 农业机械学报, 2017, 48(6): 392-398.LI Feng, FU Kaijin, YU Xiangjun. Optimization of grinding performance of large semi-autogenous mill based on hierarchical analysis[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(6): 392-398.(in Chinese)
[25] SPONG M W. Modeling and control of elastic joint robots[J]. Journal of Dynamic Systems, Measurement, and Control, 1987, 17(2): 48-55.
[26] 邢广鹏, 孙志刚, 崔向敏, 等. 多工况载荷下航空发动机支架拓扑优化设计[J]. 航空动力学报, 2020, 35(11): 2248-2262.XING Guangpeng, SUN Zhigang, CUI Xiangmin, et al. Optimised design of topology for aero-engine mounts under multi-case loads[J]. Journal of Aerospace Dynamics, 2020, 35(11): 2248-2262.(in Chinese)