0 引言
随着并联机器人的广泛应用,对其定位精度提出了更高的要求。然而,由于零件制造、装配、间隙、传动等误差因素存在,极大地限制了并联机器人在高精度领域的应用[1-2]。因此,提高并联机器人定位精度尤为重要。提高定位精度的两种常见方法是精度设计和运动学标定[3-5]。相较于精度设计,运动学标定法具有成本低、效果明显、可操作性强等优点,受到国内外学者的广泛关注。
机器人运动学标定包括4个阶段:误差模型建立、误差测量、参数辨识和误差补偿[6-7]。标定算法很大程度上依赖于误差建模阶段,误差模型建立常用方法有DH参数法[8]、螺旋理论法[9]、指数积法[10]、微分法以及摄动法[11]等。此外,LI等[12]利用遗传粒子群算法搭建神经网络,对工业机器人定位误差进行建模;CHEN等[13]提出了一种具有平行四边形结构的并联机器人误差模型;MEI等[14]提出一种弹性几何误差建模方法。各学者提出的误差建模方法为运动学标定奠定了基础,但大多学者仅在理论上建立误差模型并进行误差分析,然后提出基于所建误差模型的标定算法并开展实验,并没有通过理论推导或实验的方式对所建误差模型进行直接验证。虽然标定实验能够证明误差模型的有效性,但并不能直接说明所建误差模型的合理性与正确性。
参数辨识是机器人运动学标定的关键阶段,决定标定效率和效果[15-16]。目前,机器人运动学标定以最小二乘法为主[17],该方法原理简单、编程方式简便,但计算量较大,并且需要理论值与实际值相差不大时才有较高精度,从而限制了其应用[18]。随着智能优化算法的发展,不少学者将运动学标定问题转换为带约束条件的高维非线性方程优化问题,用智能算法求解[19]。CAO等[20]提出一种基于蝴蝶和花朵授粉算法的神经网络标定法;陈明方等[21]针对2TPR&2TPS机器人利用改进粒子群算法搭建参数辨识模型。赵磊等[22]针对3-RRRU并联机器人,利用等步距搜索策略对遗传算法进行优化。国内外学者提出的辨识方法,对机器人精度控制有很大的参考价值。
本文提出一种基于参数辨识的并联机器人误差模型验证方法,将几何结构参数误差对末端执行器位姿的影响关系映射到关节输入量上,从而用其控制机器人开展实验。以3-PUU并联机器人为对象,验证所提方法的有效性。
1 位姿误差模型建立
1.1 误差来源
影响并联机器人定位精度的因素有确定性误差和不确定性误差。其中,确定性误差包括加工制造误差和装配定位误差等几何误差,在机器人装配完成后不再改变;不确定性误差包括机器人关节间隙、负载变化造成的机构变形、振动等误差。几何误差对机器人位姿精度的影响较大[23],本文只研究几何误差因素。
并联机器人几何误差包括连杆长度误差、转动副和移动副的轴线方向误差、铰链安装位置误差,以及动平台、静平台尺寸误差等。由于这些几何误差的存在,使得末端执行器定位精度大幅降低,故将它们视为误差模型中的误差参数以及参数辨识模型中的优化变量,对其进行定量分析及标定,以提高机器人定位精度。
1.2 误差建模
运动学方程是误差建模的依据,并联机器人运动学方程可表示为
f(p,q,s)=0
(1)
式中 p——末端执行器位姿(若是六自由度机器人,则为p(x,y,z,α,β,γ))
q——关节输入量
s——几何结构参数
几何结构参数通常为常量,但由于存在加工、装配误差,实际几何结构参数与理想值之间存在偏差ds,这导致机器人在末端执行器上产生位姿误差dp,ds与dp之间满足
f(p+dp,q,s+ds)=0
(2)
为更直观地表示结构参数误差与末端执行器位姿误差之间的映射关系,对式(1)微分可得
(3)
因实际结构参数误差无法或难以通过测量的方式全部得出,故式(3)中的ds为未知量。在机器人工作空间中选取一定数量的采样点,通过设定ds值,可得到不同结构参数存在误差时对末端执行器位姿的影响。该过程即为误差分析,式(3)即通过偏微分理论建立的并联机器人误差模型。该误差建模方法通用性强、简单快捷,且物理意义明显。本文主要研究机器人结构参数误差对末端执行器位姿的影响,输入端存在误差的情况不做分析,即令误差模型中dq=0。
2 参数辨识与误差模型验证
为验证并联机器人误差模型的正确性,对其进行参数辨识,用辨识出的结构参数误差修正运动学方程,以得到实际运动学模型。在此基础上,进一步建立实际误差模型,并通过设定结构参数误差定量分析各结构参数对末端执行器位姿的影响。将该影响映射到关节输入量上,以控制机器人运动,从而开展实验。最后利用测量仪器采集末端执行器位姿,对比测量结果与误差分析结果,以验证误差模型的正确性与合理性。
2.1 运动学标定流程
机器人理想运动学模型为f(p,q,s)=0,但由于存在加工、装配误差,故实际装配情况下机器人结构参数不可能与理想值s相等。这将导致给定理想关节输入量驱动机器人后,末端执行器位姿并不等于理想位姿。为提高机器人定位精度,需建立参数辨识模型,辨识实际结构参数与理想值之间的偏差,以修正运动学模型。
并联机器人运动学标定流程如图1所示。在机器人工作空间内随机选取一定数量的理想位姿采样点,通过逆运动学方程计算出相应的理想关节输入量;用理想关节输入量驱动机器人,并利用测量仪器获取实际位姿;建立参数辨识模型;将实际位姿与理想值作差,输入参数辨识模型,获取结构参数误差;用结构参数误差修正理想结构参数,作为并联机器人运动学标定结果。
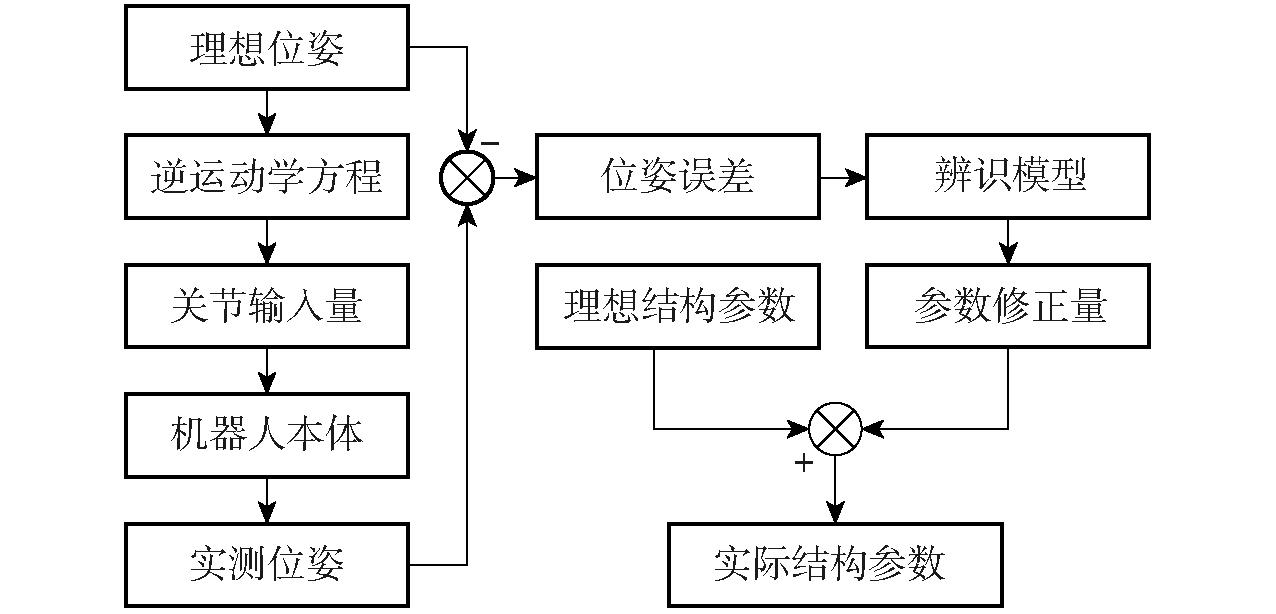
图1 并联机器人标定流程
Fig.1 Calibration process of parallel robot
2.2 参数辨识模型
因并联机器人结构参数误差对末端执行器位姿的影响很大,而实际结构参数误差又无法直接测量得出,故将结构参数误差视为相应的结构参数修正量δs。将机器人运动学标定问题转换为非线性系统优化问题,以结构参数修正量为优化变量,以末端执行器精度要求为目标设计目标函数,建立参数辨识模型。最后,利用粒子群算法求解该多参数非线性优化问题,完成机器人参数辨识。
粒子群算法(Particle swarm optimization,PSO)是非线性连续最优化问题、组合优化问题的有效求解工具,具有精度高、收敛速度快、调节参数少等优势,被广泛用于解决多目标优化、最小最大化和全局极值定位等问题[24-25]。将粒子群算法引入机器人参数辨识最优化问题求解中,算法中每个粒子位置都表示一组优化变量的解,适应度函数取得全局最优值时粒子位置即为最佳优化变量。对于并联机器人参数辨识问题,最终目标是通过调节关节输入量使得末端执行器位姿误差尽可能小,故参数辨识模型适应度函数为
(4)
式中 n——理想位姿集合中采样点数量
qj——理想关节输入量
q′j(δs)——实际位姿经逆解后含有优化变量的关节输入量
本文所提基于PSO和误差模型的参数辨识原理如图2所示。在机器人工作空间中随机取一组理想位姿,用逆运动学方程求解出关节输入量q,以控制机器人运动,同时使用测量仪器获取末端执行器实际位姿。在参数辨识模型中设定结构参数优化变量δs,将末端执行器实际位姿用含优化变量的逆运动学方程转换为关节输入量q′(δs)。随后构造优化问题的适应度函数(式(4)),设置末端执行器位姿精度要求ε,并引入粒子群算法对目标函数最小值寻优,得最优结构参数,完成参数辨识。需要指出的是,在仿真环境中无法直接得到机器人末端执行器实际位姿(p+dp),故需要在运动学模型中设定一组结构参数误差ds,从而使理想关节输入量驱动机器人时(仿真环境中表现为运动学正解),能使末端执行器位姿产生误差。同时,设定的结构参数误差也可用作判别参数辨识结果正确性的条件。而在参数辨识实验中,机器人实际位姿由测量仪器直接获得,为与仿真环境的“实际位姿”区分,将其记作p′。
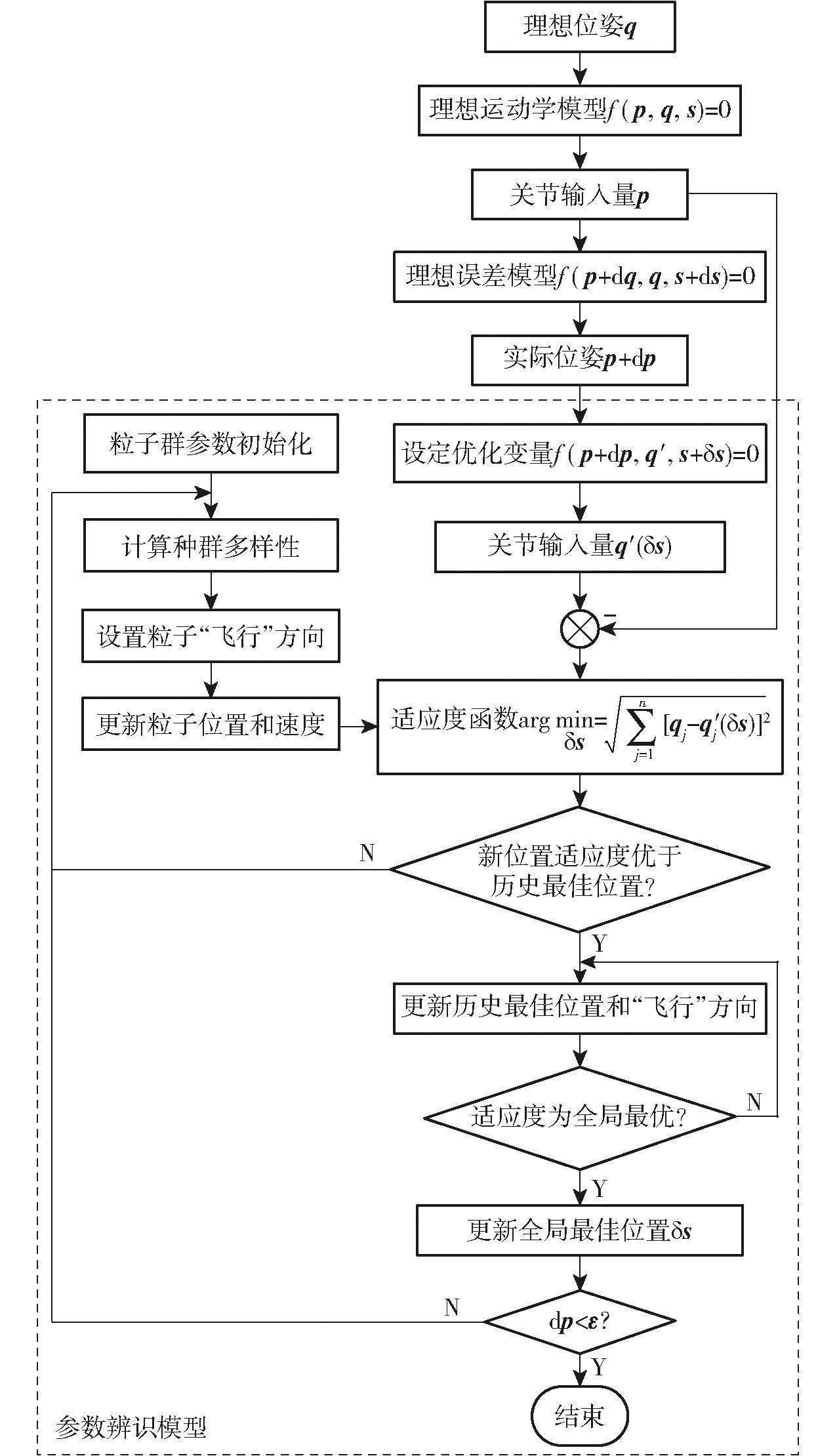
图2 参数辨识原理图
Fig.2 Principal diagram of parameter identification
2.3 误差模型验证
利用实际结构参数误差δs修正机器人结构参数得实际运动学模型
f(p,q′,s′)=0
(5)
其中
s′=s+δs
式中 q′——修正后关节输入量
s′——修正后结构参数
为验证误差模型正确性,在机器人工作空间中随机选取一定数量末端执行器位姿采样点,利用实际运动学模型逆解出相应关节输入量q′,并在得到实际运动学模型的基础上,以1.2节误差建模方式建立实际误差模型为
f(p+Δp,q′,s′+Δs)=0
(6)
式中 Δp——由设定的结构参数误差(Δs)造成的末端执行器位姿误差
Δs——结构参数误差设定值
由式(6)可知,通过设定不同结构参数误差,可分析各结构参数存在误差时对末端执行器位姿的影响关系,由末端执行器位姿误差Δp来表征,完成机器人误差分析。
为验证误差分析结果的合理性,利用实际运动学模型将各结构参数误差对末端执行器位姿的影响映射到关节输入量上,从而驱动机器人,并使用测量仪器获取误差模型验证实验中的末端执行器实际位姿p″。对比误差分析模型得到的理想位姿p+Δp与测量仪器采集到的实际位姿p″,若两者的变化趋势相同且两者间偏差很小,便能说明所建立的误差分析模型合理且正确。误差模型验证流程如图3所示。
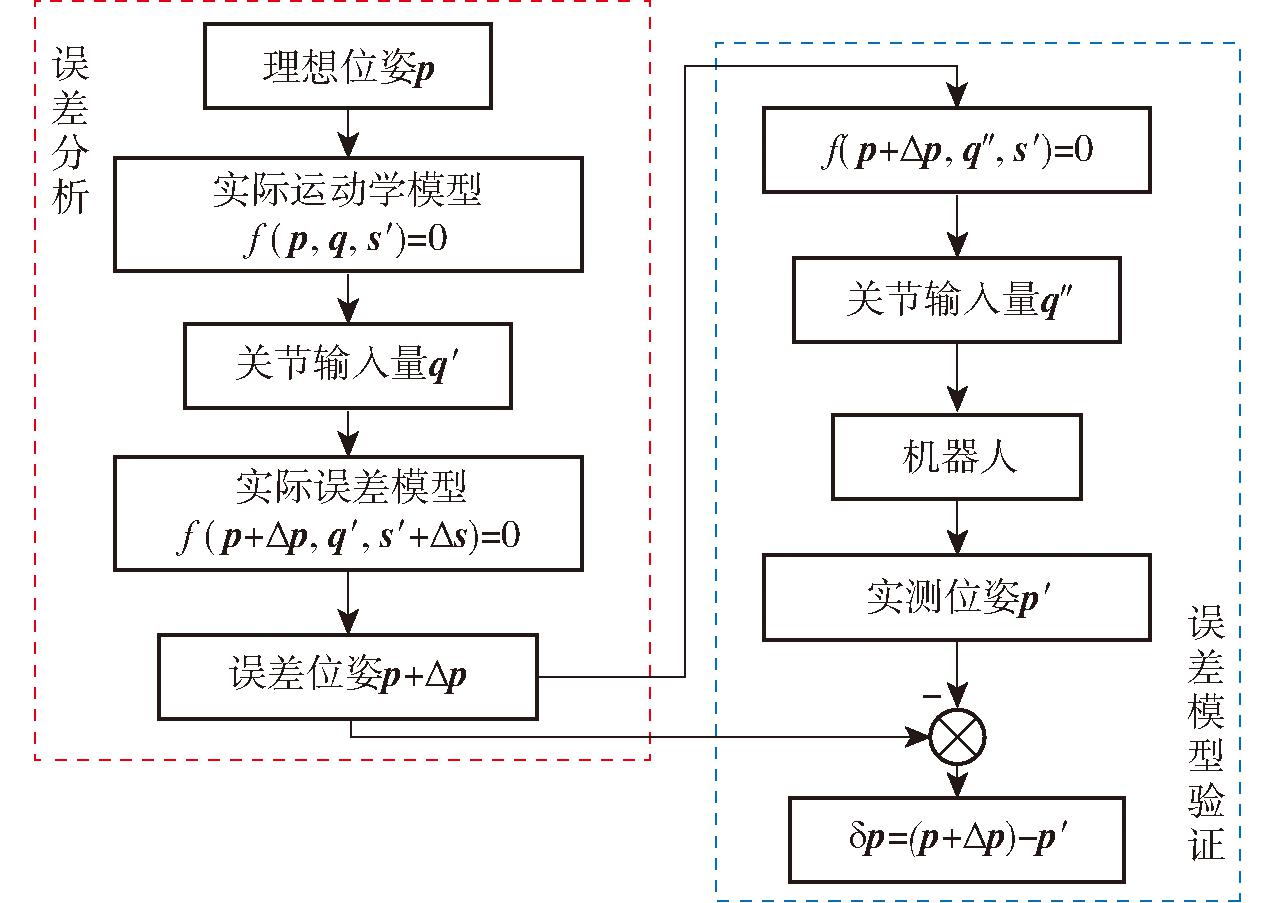
图3 误差模型验证流程图
Fig.3 Flowchart of error model verification
3 3-PUU并联机器人误差模型验证
以1台三自由度平移并联机器人为研究对象,进行基于参数辨识的并联机器人误差分析与验证。3-PUU并联机器人如图4所示,由3条完全相同的PUU支链、1个静平台以及1个动平台构成。其中P表示移动副(由丝杠、滑块组成),U表示虎克铰(由2个相互垂直的转动副R1和R2组成),3条支链呈120 °均布。将机器人简化为图5所示数学模型,其中,圆r所在平面为动平台,圆R所在平面为静平台。

图4 3-PUU并联机器人
Fig.4 3-PUU parallel robot
1.转动副 2.虎克铰 3.移动副 4.稳定杆 5.动平台 6.连杆 7.滑块 8.滚珠丝杠 9.静平台
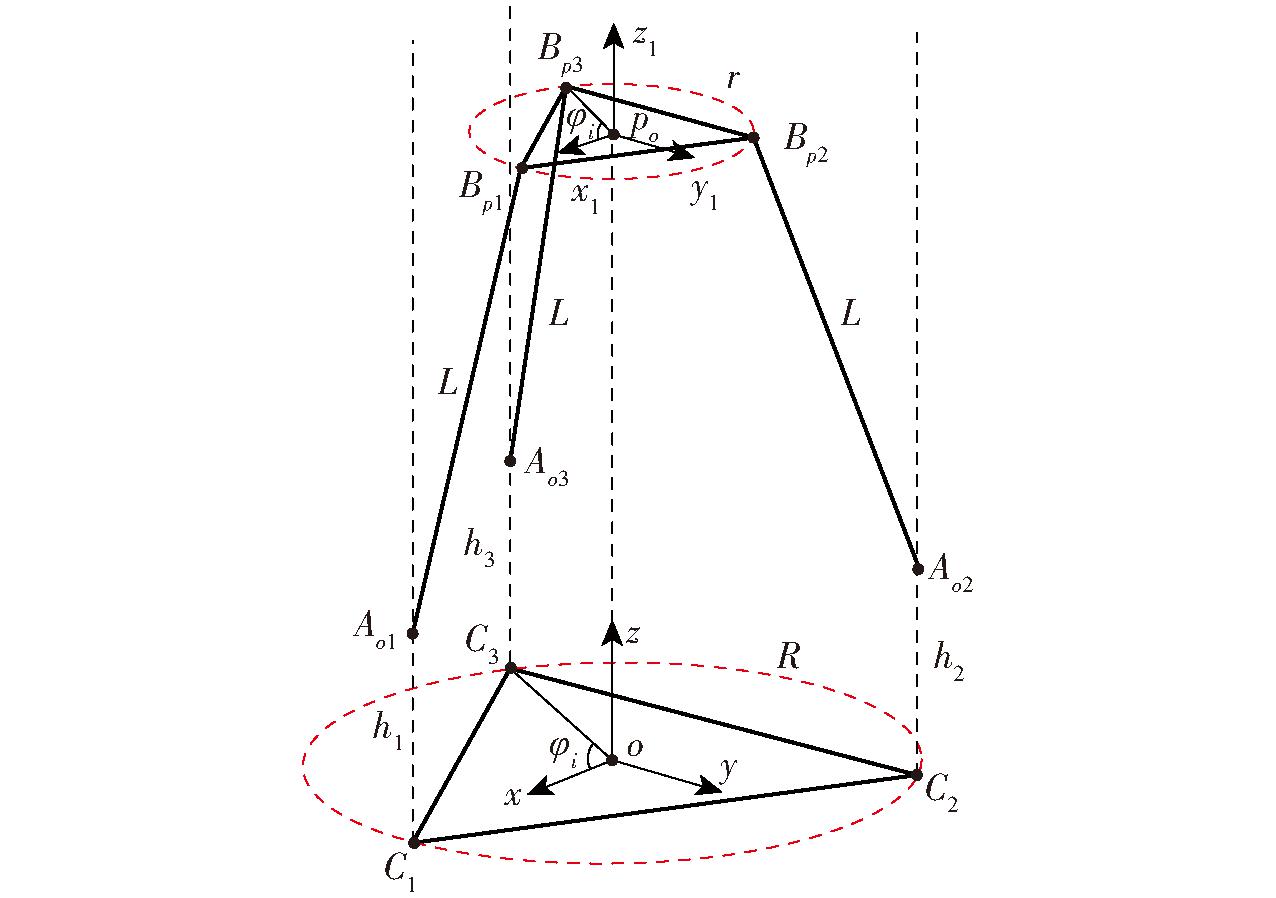
图5 简化数学模型
Fig.5 Simplified mathematical model
图5中,pox1y1z1为动坐标系,oxyz为固定坐标系。po=(X,Y,Z)为动坐标系原点在定坐标系中的表示,定义为3-PUU并联机器人末端执行器位置。3根平行四边形连杆铰接滑块连接点依次为Aoi (i=1,2,3),投影到xoy平面上为Ci,连接这3点的假想圆为静平台外接圆,半径为R=200 mm。连杆铰接动平台连接点分别为Bpi,连接这3点的假想圆为动平台外接圆,半径为r=100 mm。△C1C2C3和△Bp1Bp2Bp3为等边三角形,3条支链与x轴夹角为φi(φi=2(i-1)π/3)。hi表示在固定坐标系中滑块高度,由导轨行程以及机械结构限制有:hi∈(380,835)mm。3条支链连杆长度均为L (L=350 mm)。
3.1 运动学方程
根据图5所示的运动学坐标系,将铰链点Aoi、Bpi在固定坐标系中表示为
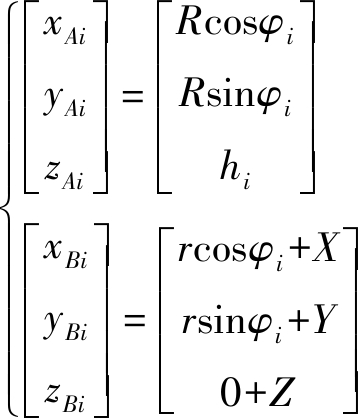
(7)
由于同一条支链上铰链点Aoi和Bpi之间的距离被连杆限制为固定值Li,由此可建立约束方程:Li=‖lAoiBoi‖,代入铰链点坐标并整理得3-PUU并联机器人理想运动学方程为
fi(p,q,s)=[X+(r-R)cosφi]2+[Y+(r-![]()
(8)
式中 X、Y、Z——3-PUU并联机器人末端执行器位置,对应式(1)中的p
hi——关节输入量,对应式(1)中的q
r、R、Li——机器人结构参数,对应式(1)中的s
3.2 误差建模
对式(8)微分得3-PUU并联机器人理想误差模型,简记为
(9)
其中

式中 diag(A)——取矩阵A的对角元素
J——机器人雅可比矩阵
N——末端执行器位置误差系数矩阵
由于本文重点研究结构参数误差对末端执行器位置的影响,故令误差模型中的滑块输入误差为零,即dhi=0。当机器人在工作空间中处于非奇异位置时,式(9)可表示为:dp=J-1N,可清晰地看出各误差参数与末端执行器位置误差间的映射关系。
3.3 参数辨识模型
3-PUU并联机器人的结构参数为r、R、L1、L2、L3,考虑对应的结构参数误差依次为dr、dR、dL1、dL2、dL3,即ds。但实际加工装配后,结构参数误差难以直接测量得到,故引入结构参数优化变量δs(δr,δR,δL1,δL2,δL3),含优化变量的运动学模型为
fi(p′,q,s+δs)={X′+[r+δr-(R+δR)]cosφi}2+{Y′+[r+δr-(R+δR)]sinφi}2+(Z′-hi)2-(Li+δLi)2=0
(10)
式中 p′(X′,Y′,Z′)——实测末端执行器位置
q(h1,h2,h3)——理想关节输入量
在仿真环境中按图2所示原理搭建3-PUU并联机器人参数辨识模型,其适应度函数为
![]()
![]()
(11)
在工作空间中随机选取30个采样点,并设置结构参数误差如表1所示。
表1 结构参数误差
Tab.1 Structural parametric errors mm
参数drdRdL1dL2dL3数值-1.02.53.4-2.82.2
如表2所示,设置参数辨识模型中粒子群优化算法各项初始参数,随后进行参数辨识仿真实验。对机器人工作空间中任取的30个末端执行器位置采样点进行结构参数误差辨识后,结果如表3所示。
表2 粒子群优化算法参数设置
Tab.2 PSO parameter setting

参数数值种群个数N500可行解维度d5惯性权重w0.8个体学习因子c10.5群体学习因子c21.2粒子位置限制-8^8粒子飞行速度限制-0.5^0.5
表3 参数辨识结果
Tab.3 Parameter identification results mm
参数δrδRδL1δL2δL3数值-0.832.673.40-2.802.20
对比表1和表3可知,本文所提参数辨识模型能准确辨识出机器人结构参数误差,其中,3条连杆长度误差辨识结果与设定值完全吻合,动平台和静平台外接圆半径误差辨识结果与设定值之间有一定偏差。原因在于3-PUU并联机器人运动学模型中,动平台和静平台外接圆半径参数总是成对出现,可将其归结为1个参数,只要辨识结果中两者差值与预设差值相同即可。
搭建如图6所示的实验平台,在工作空间中随机取30个末端执行器位置采样点进行参数辨识实验。辨识所得实际结构参数误差如表4所示。粒子群算法寻优适应度进化曲线如图7所示。
表4 机器人实际结构参数误差
Tab.4 Actual structural parametric errors of robot mm
参数δrδRδL1δL2δL3数值1.721.520.32-1.252.47

图6 实验平台
Fig.6 Experimental platform
1.激光靶标 2.激光跟踪仪 3.PC机 4. 3-PUU并联机器人
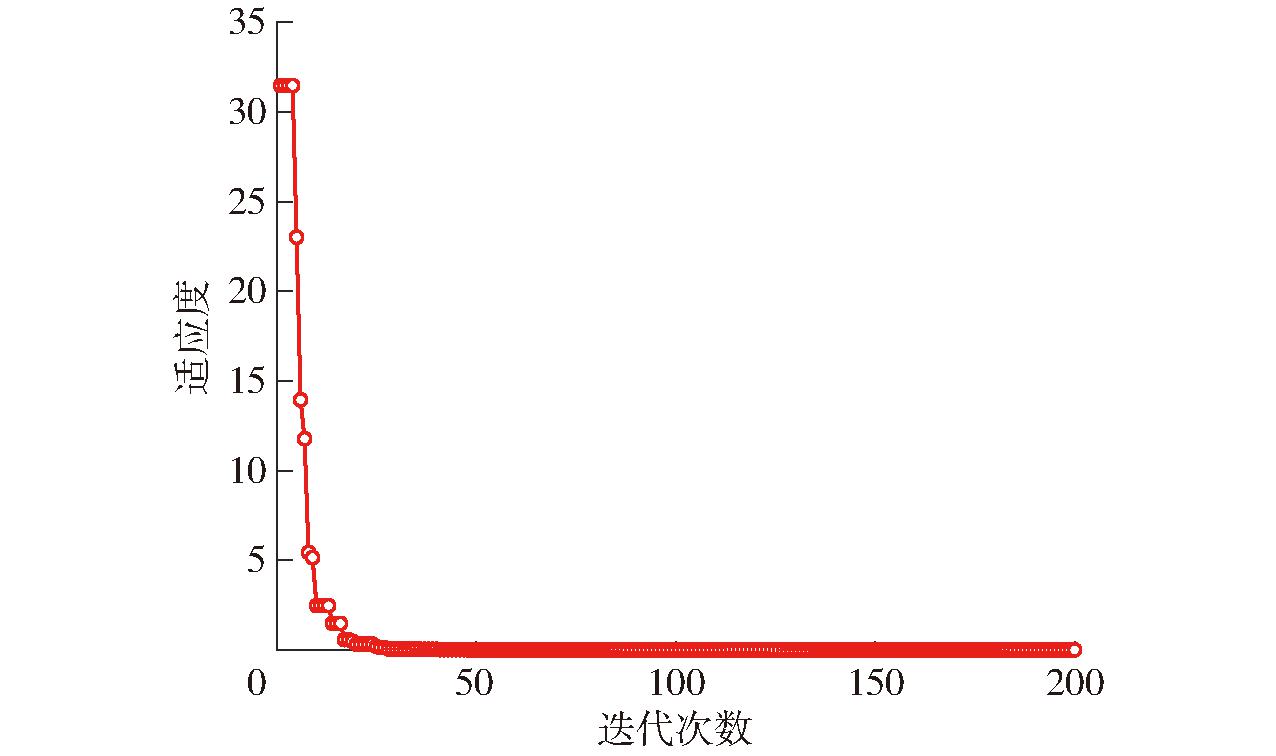
图7 适应度进化曲线
Fig.7 Fitness evolution curve
由图7可知,仅经过30次迭代,适应度由32迅速收敛到0,说明辨识算法已搜寻到一组结构参数优化变量,使实测位姿与理想值无限接近;当迭代次数达到200时,适应度为2.92×10-10,此时优化变量取值为3-PUU并联机器人实际结构参数误差。
3.4 误差建模与分析
利用表4中的实际结构参数误差修正机器人运动学方程得实际运动学模型,在此基础上建立误差模型进行误差分析与验证。该误差模型是基于参数辨识结果而建立的,故定义为实际误差模型。具体为
fi(p+Δp,q,s′+Δs)=[X+ΔX+(r′+Δr)cosφi-(R′+ΔR)cosφi]2+[Y+ΔY+(r′+Δr)sinφi-(R′+ΔR)sinφi]2+(Z+ΔZ-hi)2-(L′i+ΔLi)2=0
(12)
在滑块导轨导程内随机取10组滑块输入量h′i,对应3-PUU并联机器人工作空间的末端执行器10个位置点,作为误差分析采样点。在仿真环境中搭建实际误差模型,分Δr≠0、ΔR≠0、ΔL1≠0、ΔL2≠0、ΔL3≠0共5种情况向误差模型添加误差,因结构参数误差之间存在耦合关系,为得出各结构参数误差与末端执行器位置误差间的影响关系,在分析某误差参数的独立影响时,应确保其余误差参数的误差为零。随后将滑块输入量导入误差模型,得出误差分析结果。
3.4.1 动、静平台半径误差
在实际误差模型中分别设定动平台和静平台外接圆半径存在误差1 mm,即Δr=1 mm和ΔR=1 mm。并将10组滑块输入量导入误差模型,得出动平台、静平台外接圆半径存在误差时,10个随机位置点对应的末端执行器位置误差如图8所示。由图8可知,末端执行器在3个自由度方向上的位置误差均在1 mm内,动平台外接圆半径误差对末端执行器位置的影响与静平台相反,原因在于该机器人误差模型中,动平台、静平台半径误差参数总是成对出现(即Δr-ΔR)。
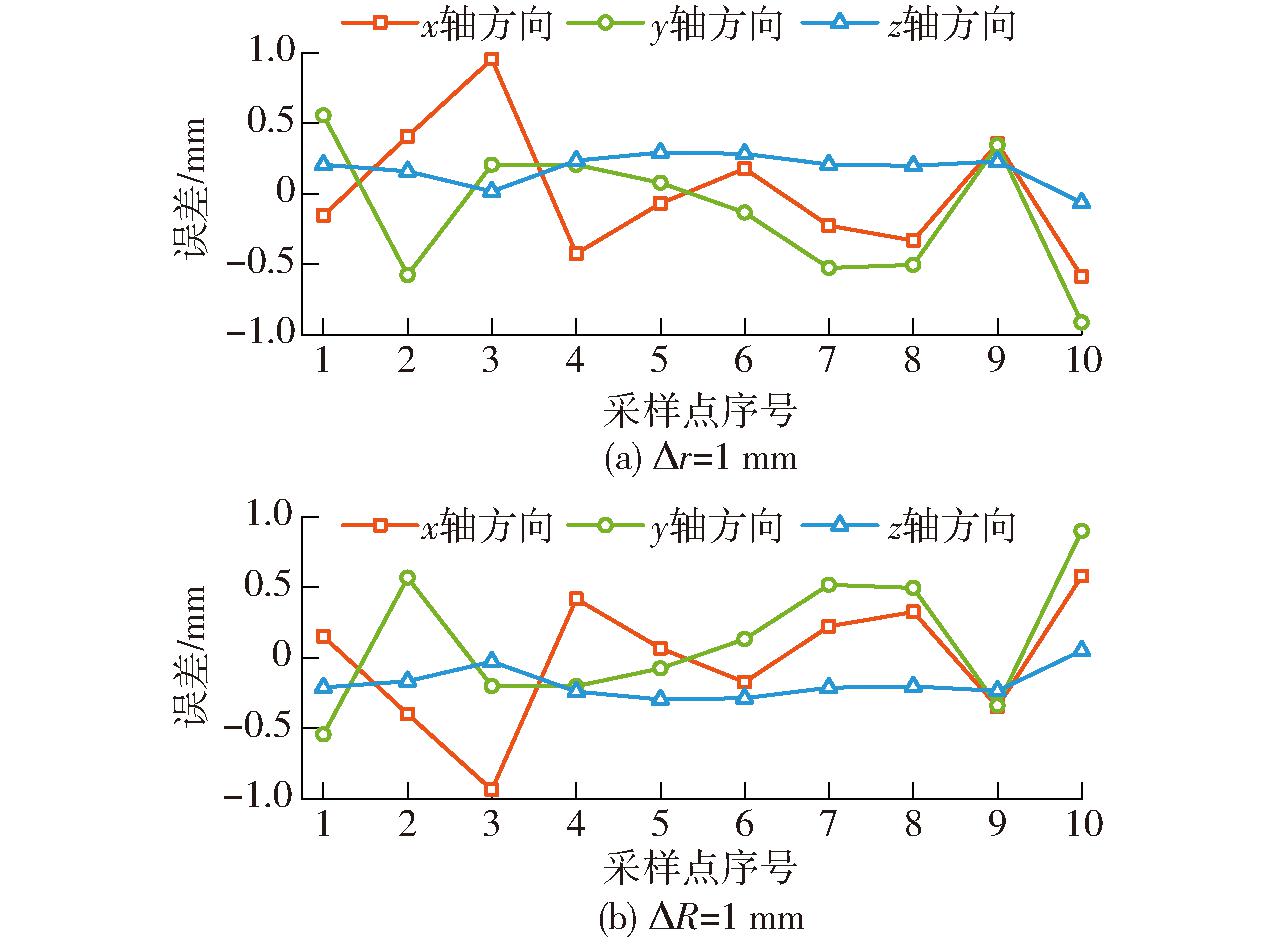
图8 动、静平台半径误差
Fig.8 Error existed in mobile and fixed platform radius
3.4.2 连杆长度误差
连杆长度存在误差可分为3种情况:ΔL1≠0、ΔL2≠0和ΔL3≠0。在仿真环境中分别设置每个误差参数误差为1 mm,导入10组滑块输入量后,可得3种情况下10个采样点对应的末端执行器位置误差如图9所示。
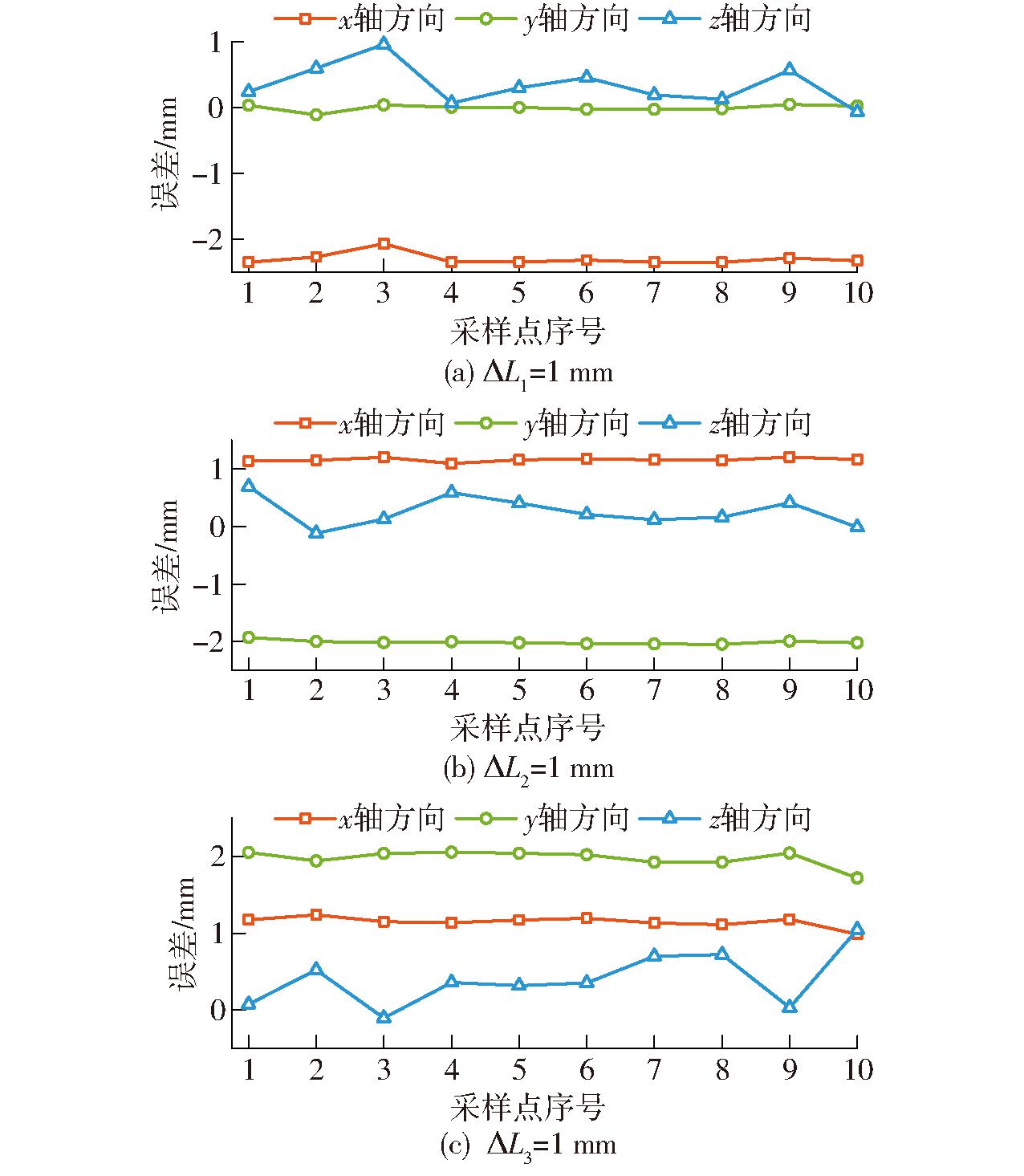
图9 连杆长度误差
Fig.9 Error existed in length of links
由图9可知,当第1条连杆长度存在误差1 mm时,末端执行器在y轴方向位置误差接近零,在z轴方向位置误差在0~1 mm内变动,x轴方向误差在-2.35 mm 附近波动;当第2条连杆长度存在误差时,末端执行器在x轴方向位置误差约为1.15 mm,在y轴方向误差约为-2.00 mm,z轴方向误差在-0.10~0.70 mm范围内变化;当第3条连杆长度存在误差时,末端执行器在x轴方向位置误差约为1.15 mm,y轴方向误差在2.00 mm附近波动,z轴方向误差在-0.10~1.05 mm范围内变动。总体来说:连杆长度存在误差时,对末端执行器在x、y轴方向的位置精度影响较大,且采样点选取对误差分析结果影响并不大,均在一个固定值附近小幅度波动。
3.5 误差模型验证
在实际操作过程中,通过加工或装配方式来精确满足误差模型中所设定的结构参数误差情况无法实现,或实现起来极其困难、成本极高。因此,本文考虑将误差模型中各误差参数对末端执行器位置的影响映射到滑块输入量上,最后通过相应的滑块输入量来驱动机器人,再使用激光跟踪仪采集末端执行器位置数据,从而验证误差模型正确性。
映射过程为:将误差分析得到的末端执行器位置数据代入机器人实际逆运动学模型中,得5种误差情况(Δr、ΔR、ΔL1、ΔL2、ΔL3)所映射的滑块输入量,最后用其控制机器人运动。使用激光跟踪仪测量此时末端执行器位置坐标,并依次计算出测量值与理想位置间的偏差,将实验得到的误差与误差模型得到的误差进行对比,以此通过实验的方式直观地验证误差模型正确性。在仿真环境中搭建模型进行仿真验证,在仿真环境中将映射的滑块输入量代入机器人实际正运动学模型,得末端执行器位置信息。图10为误差模型仿真验证结果。因3-PUU并联机器人的动平台和静平台外接圆半径误差对末端执行器位置误差的影响呈相反关系,故下文只对动平台外接圆半径存在误差情况进行分析与验证。
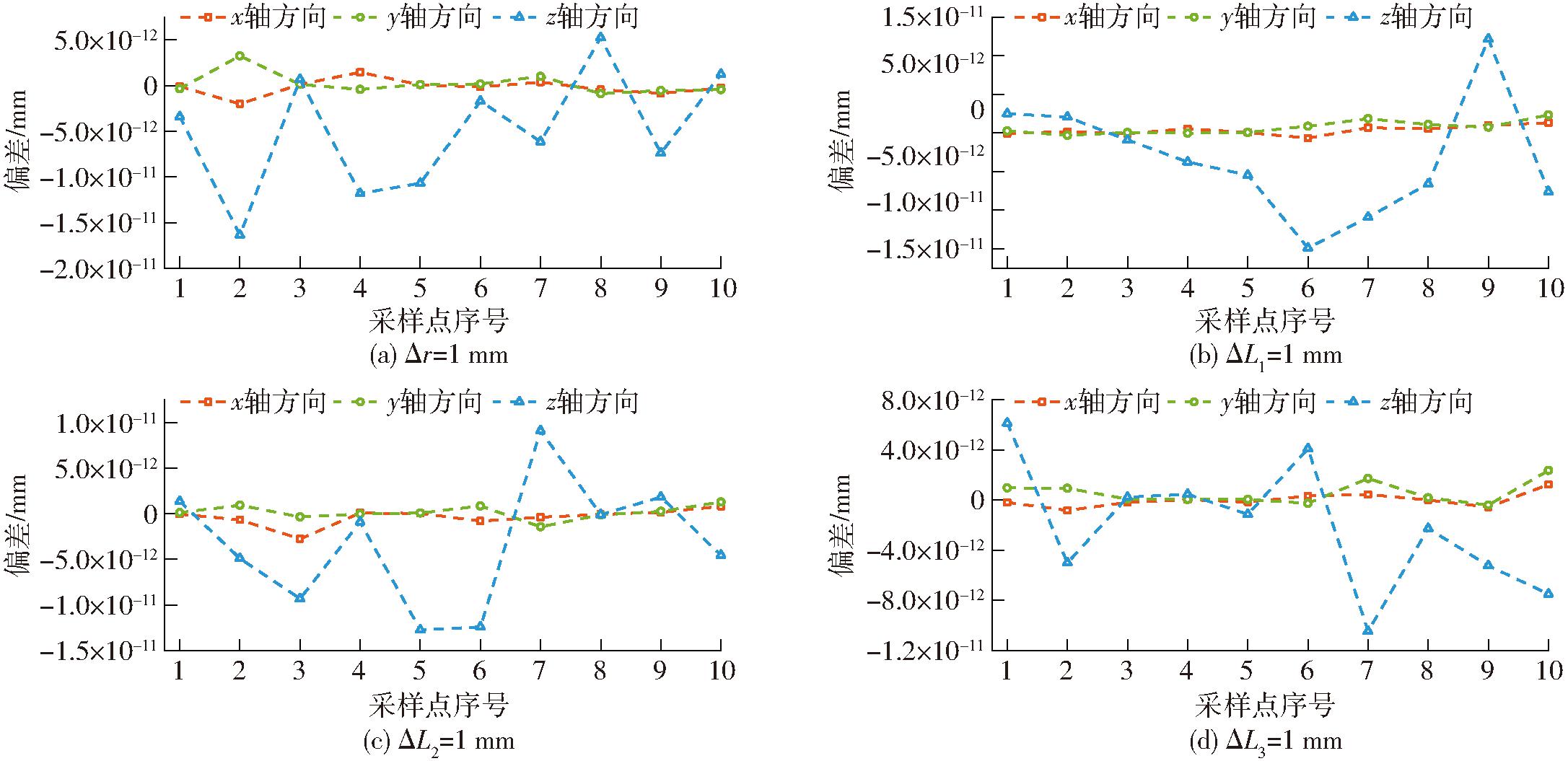
图10 误差模型验证仿真结果
Fig.10 Error model verification simulation results
由图10可知,不论是动平台外接圆半径参数存在误差的情况,还是机器人各连杆长度存在误差的情况,仿真验证结果与误差分析结果高度一致,两者之间偏差在2.0×10-11 mm以内,说明将各误差参数对末端执行器位置的影响映射到滑块输入量上,以驱动机器人直接验证误差模型正确性的方法合理。
在如图6所示的实验平台上开展误差模型验证实验,本次实验采样点在3-PUU并联机器人工作空间中随机选取,对应的理想滑块输入量如图11a所示,各误差情况下末端执行器位置映射到输入端后,滑块补偿量如图11b~11e所示。

图11 滑块输入量及映射后补偿量
Fig.11 Slider input and compensation after mapping
利用映射后的滑块输入量控制机器人运动,并使用激光跟踪仪采集末端执行器位置数据,实验结果如图12所示。由图可知,在机器人工作空间内任意位置上,实验验证结果与误差模型分析结果虽没完全重合,但两者高度拟合。为更清晰地了解误差模型分析结果与实验验证结果间的偏差,分别计算其与理想采样点位置之间各自由度方向上的误差,结果如图13所示。同时给出实验评价指标,如表5所示。
表5 实验偏差评价指标
Tab.5 Experimental deviation evaluation index mm
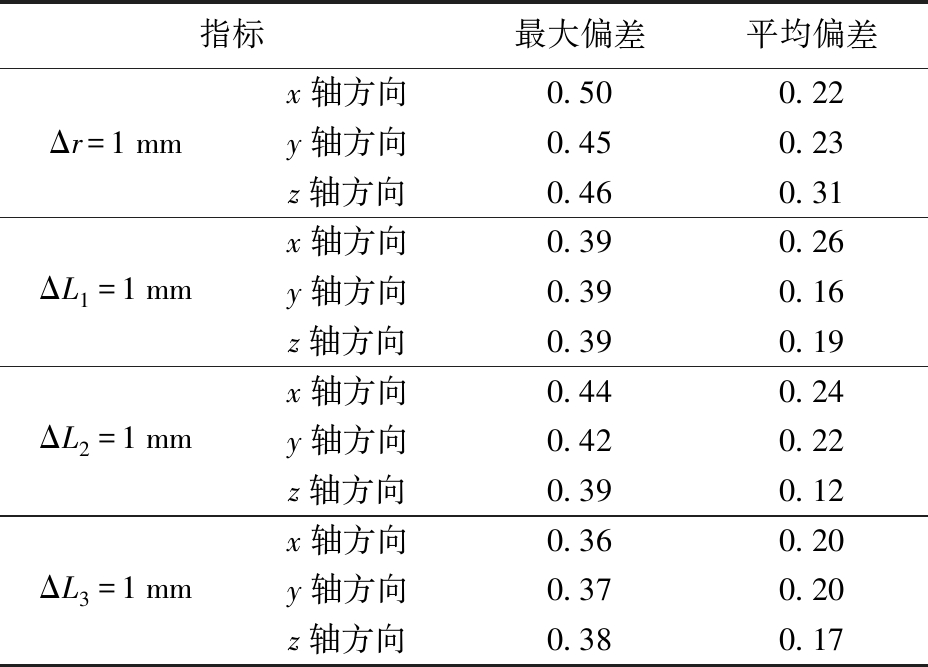
指标最大偏差平均偏差x轴方向0.500.22Δr=1mmy轴方向0.450.23z轴方向0.460.31x轴方向0.390.26ΔL1=1mmy轴方向0.390.16z轴方向0.390.19x轴方向0.440.24ΔL2=1mmy轴方向0.420.22z轴方向0.390.12x轴方向0.360.20ΔL3=1mmy轴方向0.370.20z轴方向0.380.17
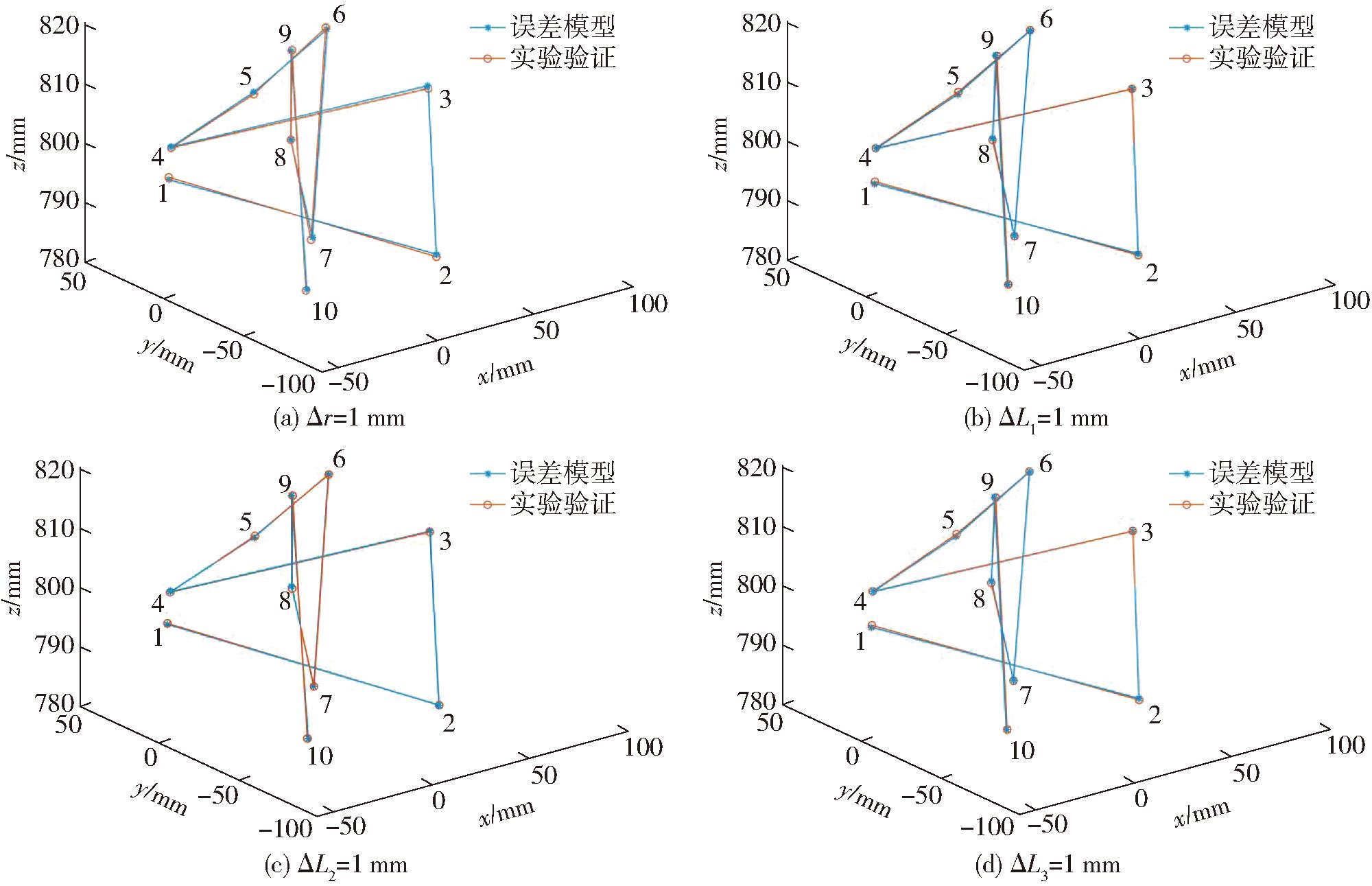
图12 误差模型验证实验结果
Fig.12 Error model verification experimental results
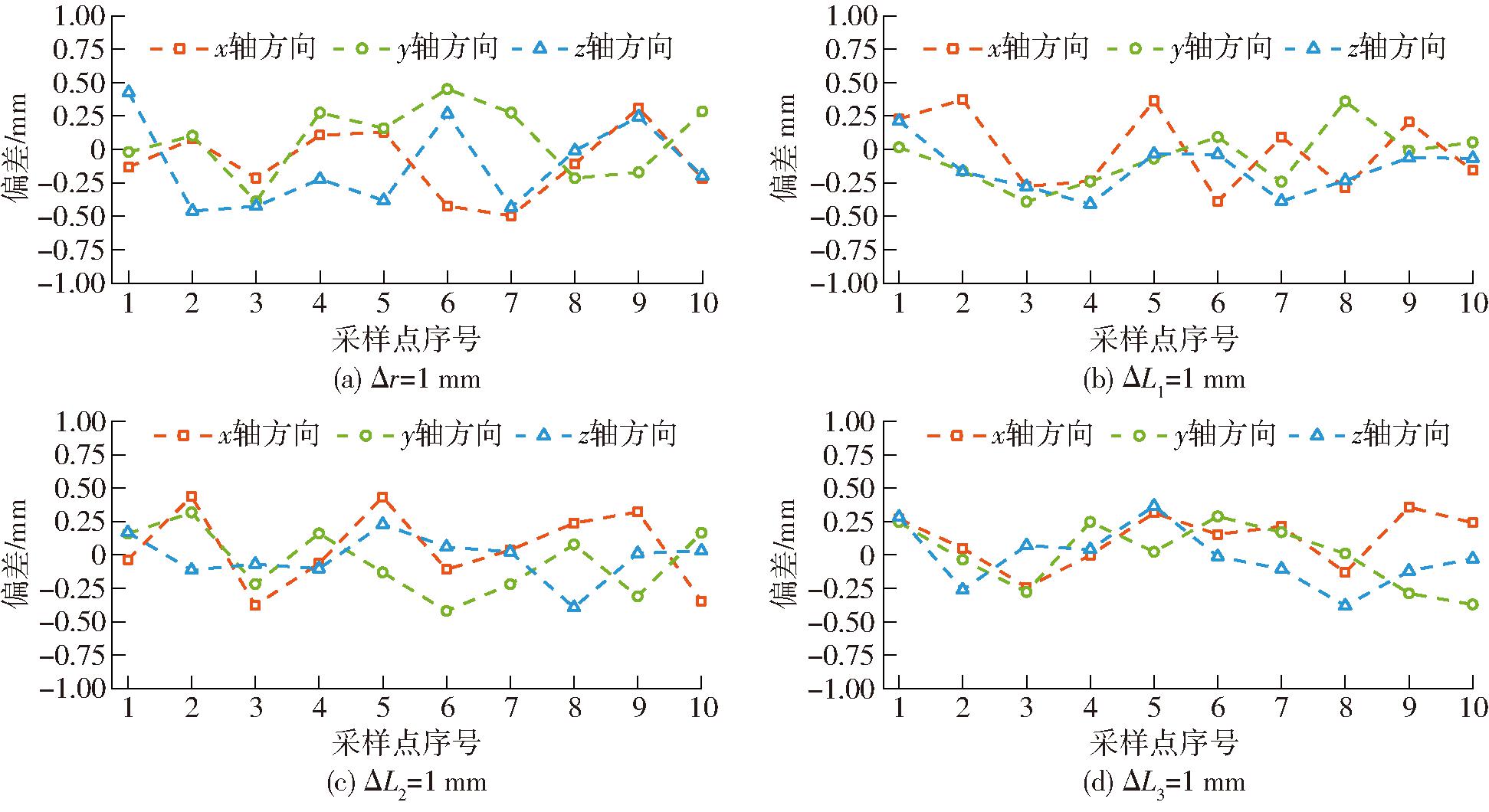
图13 实验结果与误差模型分析结果偏差
Fig.13 Deviation between experimental results and error model analysis results
由表5和图13可知,实验结果与误差模型分析结果之间存在一定的偏差,但偏差较小,这是由未考虑误差模型的机器人输入端误差、关节间隙误差等因素造成的。在实验验证中,最大偏差出现在 Δr=1 mm时的第7个采样点x轴方向,偏差为0.50 mm;其次当Δr=1 mm时的第2个采样点z轴方向,偏差为0.46 mm;其余最大偏差均保持在0.45 mm以内。此外,实验涉及到的随机采样点平均偏差,除Δr=1 mm时z轴方向偏差以及ΔL1=1mm时x轴方向偏差之外,其余平均偏差均小于0.25 mm。总体来说,实验结果与误差模型分析结果的误差趋势相同,且两者间的偏差基本保持在0.45 mm以内,说明将各误差参数对末端执行器位置的影响映射到滑块输入量上驱动机器人验证所建误差模型方法正确、可行。
4 结论
(1)在参数辨识基础上,提出了一种并联机器人误差模型验证方法。该方法将机器人几何结构参数误差对末端执行器位姿的影响关系映射到关节输入量上,从而可用关节输入量控制机器人运动,以开展误差模型验证实验。
(2)以3-PUU并联机器人为对象构建参数辨识模型,辨识出结构参数误差并修正运动学方程,得到了实际运动学模型。在此基础上,建立机器人实际误差模型并进行误差分析,随后将各误差参数对末端执行器位置的影响依次映射到滑块输入量上,用其控制机器人运动后使用激光跟踪仪采集末端位置数据。实验结果表明,激光跟踪仪采集到的末端执行器位置数据与误差模型分析结果之间最大偏差为0.50 mm,平均偏差在0.31 mm以内,验证了误差模型的正确性。
[1] LI Z B, LI S, LUO X. An overview of calibration technology of industrial robots[J]. IEEE/CAA Journal of Automatica Sinica, 2021, 8(1): 23-36.
[2] 齐飞,张恒,裴海珊,等. 基于力传递模型的连续体机器人驱动误差补偿研究[J]. 农业机械学报,2023,54(1):402-411.QI Fei, ZHANG Heng, PEI Haishan, et al. Drive error compensation of continuum manipulator based on force transfer model[J]. Transactions of the Chinese Society for Agricultural Machinery, 2023, 54(1): 402-411. (in Chinese)
[3] LI B, WEI T, ZHANG C, et al. Positioning error compensation of an industrial robot using neural networks and experimental study[J]. Chinese Journal of Aeronautics, 2022, 35(2): 346-360.
[4] TIAN W, HUO M, ZHANG X, et al. A general approach for robot poses error compensation based on an equivalent joint motion error model[J]. Measurement, 2022, 203: 111952.
[5] WANG W, TIAN W, LIAO W, et al. Error compensation of industrial robot based on deep belief network and error similarity[J]. Robotics and Computer-Integrated Manufacturing, 2022, 73: 102220.
[6] LI C, WU Y, LI Z. POE-based robot kinematic calibration using axis configuration space and the adjoint error model[J]. IEEE Transactions on Robotics, 2016, 32(5): 1264-1279.
[7] 夏纯,张海峰,李秦川,等. 基于等效运动链的并联机器人运动学标定方法[J]. 机械工程学报,2022,58(14):71-84.XIA Chun, ZHANG Haifeng, LI Qinchuan, et al. Novel kinematic calibration method of parallel mechanisms using the equivalent kinematic chains[J]. Journal of Mechanical Engineering, 2022, 58(14): 71-84. (in Chinese)
[8] LEE S, ZENG Q, EHMANN K F. Error modeling for sensitivity analysis and calibration of the tri-pyramid parallel robot[J]. The International Journal of Advanced Manufacturing Technology, 2017, 93(5):1319-1332.
[9] YANG C, LU W, XIA Y. Positioning accuracy analysis of industrial robots based on non-probabilistic time-dependent reliability[J]. IEEE Transactions on Reliability, 2024, 73(1): 608-621.
[10] 乔贵方,杜宝安,张颖,等. 基于POE模型的工业机器人运动学参数二次辨识方法研究[J]. 农业机械学报,2024,55(1): 419-425.QIAO Guifang, DU Baoan, ZHANG Ying, et al. Quadratic identification method of kinematic parameters of industrial robot based on POE model[J]. Transactions of the Chinese Society for Agricultural Machinery, 2024, 55(1): 419-425. (in Chinese)
[11] 徐卫良. 机器人机构误差建模的摄动法[J]. 机器人,1989, 11(6):39-44,48.XU Weiliang. A perturbation approach to error modeling of robot likage[J]. Robot, 1989, 11(6): 39-44,48. (in Chinese)
[12] LI B, WEI T, ZHANG C, et al. Positioning error compensation of an industrial robot using neural networks and experimental study[J]. Chinese Journal of Aeronautics, 2022, 35(2): 346-360.
[13] CHEN Y Z, LIU X Y, ZHOU Y, et al. Error modeling and sensitivity analysis of a parallel robot with SCARA (selective compliance assembly robot arm) motions[J]. Chinese Journal of Mechanical Engineering, 2014, 27(4): 693-702.
[14] MEI B, XIE F, LIU X J, et al. Elasto-geometrical error modeling and compensation of a five-axis parallel machining robot[J]. Precision Engineering, 2021, 69: 48-61.
[15] 毕松,王宇豪. 果园机器人视觉导航行间位姿估计与果树目标定位方法[J]. 农业机械学报,2021,52(8):16-26. BI Song, WANG Yuhao. Inter-line pose estimation and fruit tree location method for orchard robot[J]. Transactions of the Chinese Society for Agricultural Machinery, 2021, 52(8): 16-26. (in Chinese)
[16] PERRUSQUIA A, GARRIDO R, YU W. Stable robot manipulator parameter identification: a closed-loop input error approach[J]. Automatica, 2022, 141: 110294.
[17] LUO G, ZOU L, WANG Z, et al. A novel kinematic parameters calibration method for industrial robot based on Levenberg-Marquardt and differential evolution hybrid algorithm[J]. Robotics and Computer-Integrated Manufacturing, 2021, 71: 102165.
[18] 刘毅,金晖力,丰宗强,等. 基于点球约束的机器人误差建模与参数辨识[J]. 工程科学与技术,2023,55(6):222-235.LIU Yi, JIN Huili, FENG Zongqiang, et al. Error modeling and parameter identification for robots based on point-sphere constraints[J]. Advanced Engineering Sciences, 2023, 55(6): 222-235. (in Chinese)
[19] GROVER J, LIU C, SYCARA K. Parameter identification for multirobot systems using optimization-based controllers[C]∥2021 International Symposium on Multi-Robot and Multi-Agent Systems (MRS), 2021: 173-180.
[20] CAO H Q, NGUYEN H X, TRAN T N C, et al. A robot calibration method using a neural network based on a butterfly and flower pollination algorithm[J]. IEEE Transactions on Industrial Electronics, 2022, 69(4): 3865-3875.
[21] 陈明方,何朝银,张永霞,等. 2TPR&2TPS并联机器人结构参数辨识[J]. 农业机械学报,2023,54(10):421-431. CHEN Mingfang, HE Chaoyin, ZHANG Yongxia, et al. Structural parametric identification of 2TPR&2TPS parallel robot[J]. Transactions of the Chinese Society for Agricultural Machinery, 2023, 54(10): 421-431. (in Chinese)
[22] 赵磊,闫照方,栾倩倩,等. 大空间运动3-RRRU并联机器人运动学标定与误差分析[J]. 农业机械学报,2021,52(11):411-420.ZHAO Lei, YAN Zhaofang, LUAN Qianqian, et al. Kinematic calibration and error analysis of 3-RRRU parallel robot in large overall motion[J]. Transactions of the Chinese Society for Agricultural Machinery, 2021, 52(11): 411-420. (in Chinese)
[23] 刘伟,刘顺,邓朝晖,等. 工业机器人定位误差补偿技术研究进展[J]. 机械工程学报,2023,59(17):1-16.LIU Wei, LIU Shun, DENG Zhaohui, et al. Research progress of positioning error compensation technology for industrial robots[J]. Journal of Mechanical Engineering, 2023, 59(17): 1-16 (in Chinese)
[24] SHAMI T M, ELSALEH A A, ALSWAITTI M, et al. Particle swarm optimization: a comprehensive survey[J]. IEEE Access, 2022, 10: 10031-10061.
[25] WANG R, HAO K, CHEN L, et al. A novel hybrid particle swarm optimization using adaptive strategy[J]. Information Sciences, 2021, 579: 231-250.