0 引言
农业机械自动导航是智慧农业的关键技术之一,在农作物精准生产中起到重要作用[1-3]。在农机导航系统中,前轮转角检测装置和电动方向盘是其重要的动作执行部分[4-5],前轮转角是车辆状态反馈信息,通过控制电动方向盘,实现转向闭环控制[6]。前轮转角检测精度直接影响农机路径跟踪的精度和稳定性。
相关学者对转角检测方法进行了较多研究。最简单的方法是将传感器安装在一侧前轮来直接或间接测量前轮转角。何杰等[7]、NAGASAKA等[8]在插秧机前轮转向柱上安装角度传感器,直接测量插秧机的前轮转角;房素素等[9]、陈文良等[10]用角位移传感器测量液压油缸行程,通过标定传感器输出电压和角度的线性关系计算出前轮实际转角;胡书鹏等[11]结合前轮转向过程,提出了位移式间接转角测量法和四连杆式间接转角测量法;DONG等[12]用角度传感器测量前轮转角,根据阿克曼转向原理构建梯形转向模型,从而得到更准确的转角;但是角度传感器安装复杂,受转向机械间隙影响大[13-14],标定困难[15],并且随着机械支架老化,传感器零位测量不准确。针对零位不准确的问题,一些学者提出采用运动学转角对轮角测量修正的方法。Trimble公司提出基于前轮陀螺仪估计转角的方法,在拖拉机前轮安装陀螺仪测量前轮转角速度,根据拖拉机运动学模型获取运动学转角,卡尔曼滤波器实时融合计算出前轮转角[16];WANG等[17]、缪存孝等[18]在此基础上增加了陀螺仪偏置的在线估计和速度杆臂误差消除方法来提高陀螺仪估计前轮转角的精度。在转向机构上加装传感器的方法造成传感器及其线缆暴露在农机外壳上,在实际生产过程中容易受到作物的剐蹭、碰撞,从而导致传感器或其线束受损,因此一些学者开始研究无轮角传感器的转角估计方法。陈云等[19]设计了基于GNSS(Global navigation satellite system)模块和电动方向盘编码器的转角测量系统,对方向盘角速度和全液压转向阀建立线性模型,用方向盘角速度推算出转角速度,用卡尔曼滤波器融合解算出转角。HUANG等[20]提出方向盘和传动轴的间隙模型,通过递归优化辨识量化机械间隙,结合转向动力学模型推导出前轮转角。何杰等[21]建立了履带底盘的虚拟阿克曼转角和直线跟踪航向偏差的转向模型,用卡尔曼滤波器解算出履带花生收获机的等效转角。KHAN等[22]采用外控非线性自回归模型来拟合两轮转向机器人的动力学模型,模型根据两轮转速差直接获得等效转角和航向角。可见,无轮角传感器的转角估计难点集中在装备的转向系统模型建立上。
本文提出一种基于ARMAX-KF和速度补偿的无轮角传感器转角估计方法,用农机导航系统中双BDS-GNSS定位天线、车身姿态传感器和电动方向盘来测量农机的位置、速度、姿态、车身角速度以及方向盘角速度等信息,采用ARMAX时间序列分析方法对拖拉机转向系统进行建模,简化拖拉机转向系统建模难度,利用ARMAX模型预测转角速度,结合拖拉机的运动学转角,采用卡尔曼滤波器融合解算得到前轮实时转角。
1 转角估计系统与方法
1.1 试验平台和系统组成
选用雷沃欧豹M704-2H型拖拉机为试验平台,拖拉机转向传动比为10.5,平台搭载农机导航系统,试验平台实物如图1所示。其中,农机导航系统转向执行机构采用华测导航公司的CES-T型电动方向盘,内置编码器分辨率为0.035°,通过对编码器值微分获得方向盘角速度,输出频率为50 Hz;前轮转角速度测量IMU(Inertial measurement unit)采用Xsens公司的MTi-28A53G35型陀螺仪,分辨率为0.01(°)/s;左前轮转角测量采用世纪铭创公司的MCJSV05B型角度传感器,分辨率为0.022°;定位采用和芯星通公司的UB482型BDS-GNSS定位板卡,板卡输出频率为10 Hz,RTK固定解状态下平面定位精度为1 cm±1ppm(ppm为与基站距离每千米增加1 mm误差),对地运动速度测量精度为0.03 m/s,航向精度为0.2(°)/1 m基线;车身姿态传感器采用凌思科技公司的LINS16460型六轴惯性传感器,横滚俯仰姿态测量精度小于0.3°,三轴角速度测量精度为0.01(°)/s。前轮转角估计系统结构如图2所示。
图1 雷沃M704-2H型试验平台
Fig.1 LOVOL M704-2H test platform
1.电动方向盘 2.前轮转角速度测量IMU 3.前轮轮角角度传感器 4.双BDS-GNSS定位天线 5.导航控制器 6.车身姿态传感器
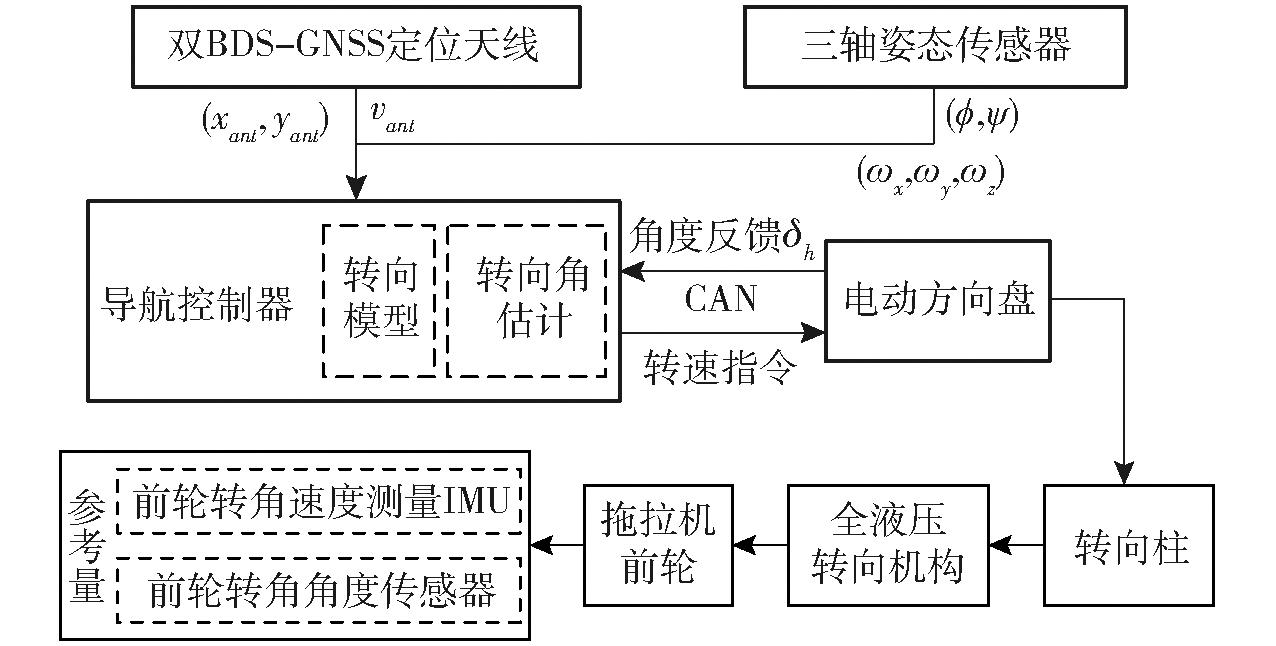
图2 前轮转角估计系统结构框图
Fig.2 System structure block diagram of steering angle estimation system
图2中,系统双BDS-GNSS定位天线获取主天线的运动速度vant、横摆角θ以及主天线的高斯-克吕格直角平面坐标系下的东向和北向坐标位置xant、yant;姿态传感器获取拖拉机横滚俯仰姿态角φ、ψ和三轴角速度ωx、ωy、ωz;电动方向盘获取方向盘角度δh。控制器完成转角估计并做出转向决策,向电动方向盘发送转向指令,方向盘带动转向柱,转动全液压转向机构,最后推动拖拉机前轮。拖拉机左前轮还安装角度传感器和IMU,用以测量前轮转角和测量转角速度,并作为本文方法估计精度评判的参考指标。
1.2 拖拉机运动学模型
根据阿克曼转向原理,拖拉机转向时,内侧轮转角和外侧轮转角存在差异,假设拖拉机作业地面平坦、行驶速度变化小、忽略轮胎侧向滑移,拖拉机可以被抽象为二轮车运动学模型,如图3所示。图3中,点C为拖拉机转向旋转中心;点P为后轮轴中心接地点;R为转弯半径,m;B为左右前轮轮距,m;L为前后轮轴距,m;vP为后轮轴接地点速度,m/s;α为左前轮相对于车头方向的角度,(°);δkin为简化二轮模型的虚拟转角,即阿克曼虚拟转角,(°);θ为拖拉机横摆角,(°)。
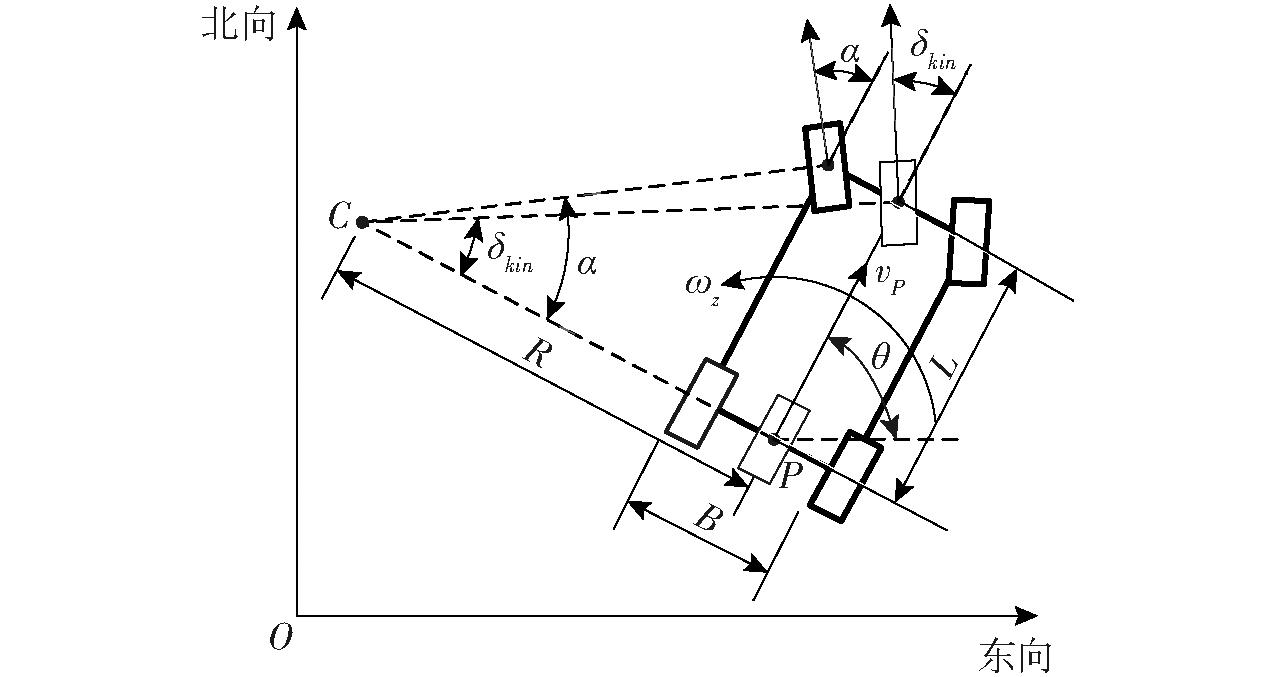
图3 拖拉机运动学模型示意图
Fig.3 Schematic of kinematic model of tractor
δkin为拖拉机阿克曼虚拟转角,即拖拉机运动学转角,本文规定转角中位为零位,左偏为正,右偏为负,根据角速度公式,利用横摆角速度和后轮轴中心接地点速度可以推导出运动学转角为
(1)
根据式(1),拖拉机横摆角速度ωz可以由姿态传感器测量获得,后轮轴中心接地点速度vP可以由双BDS-GNSS定位天线速度结合拖拉机的姿态和角速度获得,从而得到拖拉机运动学转角。但ωz和vP存在测量噪声,并且在速度较低时运动学转角计算误差大,所以直接用运动学转角来做转向控制精度较低。
其中,左前轮角度传感器直接测量的是左前轮相对于车头方向的角度,需转换成参考前轮转角δ*,计算公式为
(2)
1.3 算法框架
本文提出了一种结合ARMAX模型和卡尔曼滤波器的转角估计方法,即ARMAX-KF。首先用ARMAX模型作为辨识模型,辨识出拖拉机方向盘角速度-转角速度转向系统; ARMAX模型可以预测出转角速度预测值ωh,δ,ωh,δ积分后获得转角,但其积分结果存在建模误差;式(1)的运动学转角为绝对角度,二者可以进行互补,故依靠卡尔曼滤波器的校正特性,以运动学转角作为观测值,修正积分中的误差,提高估计精度,本文算法框架如图4所示。图4中,k为采样时刻;ωh为电动方向盘角速度,(°)/s;z-1为延迟算子;ωδ,h为ARMAX模型预测转角速度,(°)/s;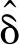
-为转角估计先验估计值,(°);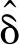为转角估计值,
为卡尔曼滤波器测量值,(°)。
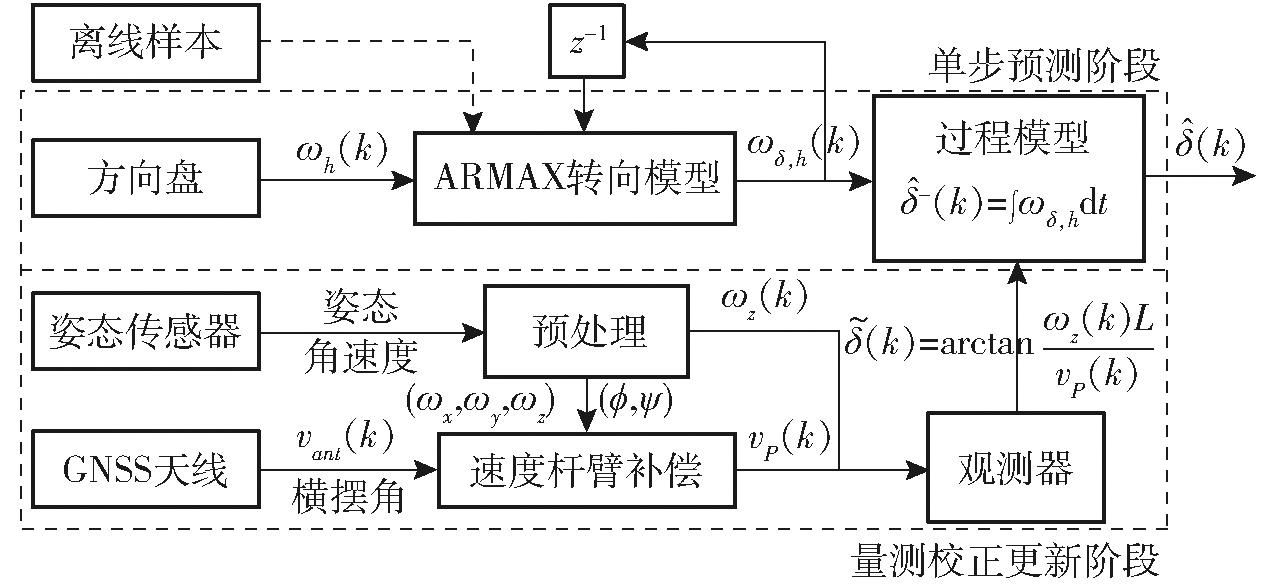
图4 算法框架
Fig.4 Algorithm framework
2 转向模型辨识
2.1 拖拉机转向模型
拖拉机转向模型输入为方向盘角速度,输出为转角速度。方向盘角速度输入到传动轴,经过全液压转向器后,液压推杆推动拖拉机前轮,实现转向。而拖拉机全液压转向器[23]、液压缸[24]等液压元件中存在着油隙、内泄、迟滞和死区等特性;拖拉机方向盘和前轮转角转向系统可以看作为典型单输入Hammerstein非线性模型[25],如图5所示。图5中,F(z)为有源非线性函数,包括滞后、间隙、死区等;G(z)为模型中线性环节的传递函数;N(z)为噪声模型传递函数;u为方向盘角速度;
为内部输入,不可测量;x为真实输出;y为转角速度;ε为系统随机扰动,属于零均值标准化白噪声序列;ξ为有色噪声。
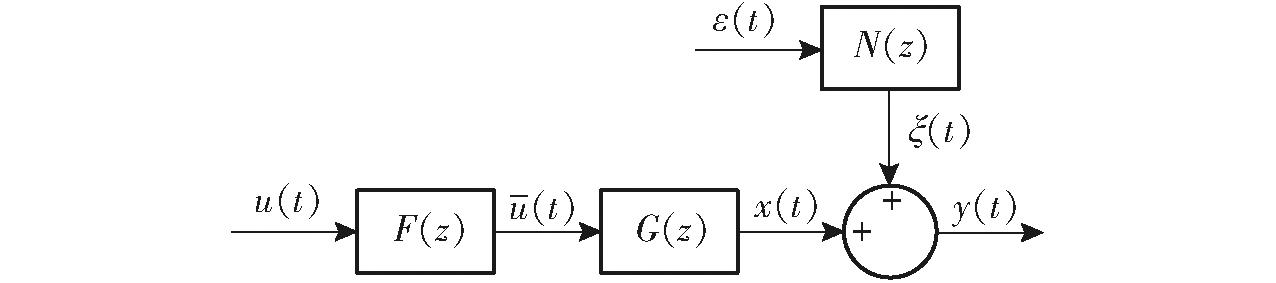
图5 转向系统一般模型
Fig.5 General model of steering system
拖拉机转向系统可用一个n阶的定常数函数表示为
(3)
其中
(4)
(5)
(6)
式中 A(z)、Bm(z)、C(z)——单位延迟定常时不变多项式
F(z)非线性部分不易直接测量,一般采用满足要求精度的近似函数来表示,采用n阶泛函级数表示为
(7)
式中 Bμ——泛函级数
μ——泛函级数系数
令B(z)=Bm(z)Bμ(z),拖拉机转向系统可近似表示为
A(z)y(t)=Bm(z)Bu(z)u(t)+C(z)ε(t)=B(z)u(t)+C(z)ε(t)
(8)
由于方向盘角速度-转角速度的转向系统属于定常系统,并且考虑到转角受方向盘角速度驱动,转角速度具有时序特性,本文采用ARMAX模型来表示拖拉机转向模型,模型参数可以通过转向样本进行拟合获得。
2.2 基于ARMAX模型的转向模型建立
时间序列分析的基本思想为,建立能够比较精确地反映时间序列中所包含动态依存关系的数学模型,根据观察历史数据来评价事件现状和估计事件未来变化,并对系统未来行为进行预测。ARMAX是时间序列分析中应用非常广泛的线性系统模型之一,通过将时间序列过程拟合成一组多项式,这组多项式可用来预测时间序列未来状态,常用于时序预测、系统辨识和滤波器设计[26-27]。
ARMAX模型中包括AR(自回归模型)、MA(滑动平均模型)和X(外生输入模型)[28],分别表示输出、随机扰动和输入样本的回归项。ARMAX输出结果与历史输出、随机扰动和外部输入的当前值及过去值有关,其ARMAX模型推广形式为
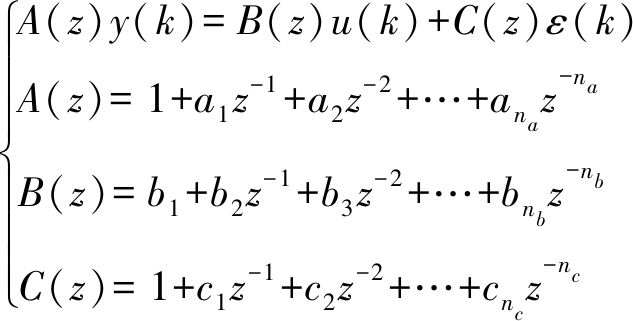
(9)
式中 na、nb、nc——自回归模型、外生输入模型和滑动平均模型滞后阶数
ai、bi、ci——对应序列的模型参数
y(k)——输出序列第k时刻输出
u(k)——输入序列第k时刻输入
ε(k)——零均值标准化白噪声干扰序列第k时刻实时噪声
在拖拉机转向系统中ARMAX模型表示为
(10)
式中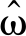 
δ,h——模型期望输出,即ARMAX模型预测转角速度,(°)/s
在实际过程中,模型的随机噪声序列无法测量,实际使用时忽略掉噪声回归项,记e(k)=C(z-1)ε(k),通过ARMAX模型计算出的转角速度ωδ,h为
ωδ,h(k)=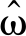δ,h(k)-e(k)=
(11)
2.3 ARMAX模型参数拟合辨识
转向系统属于常系数系统,所以在实际应用中,通过首次的离线样本(方向盘角速度和转角速度)对其模型参数进行拟合后便能获得转向系统的近似模型。方向盘角速度和转角速度可以分别通过对电动方向盘角度、运动学转角进行微分获得,计算式为
(12)
(13)
式中 Δt——计算周期,取0.02 s
测量转角速度
本文采用RLS法来进行ARMAX模型的参数拟合[29-30],定义测量数据向量和需拟合的参数向量为
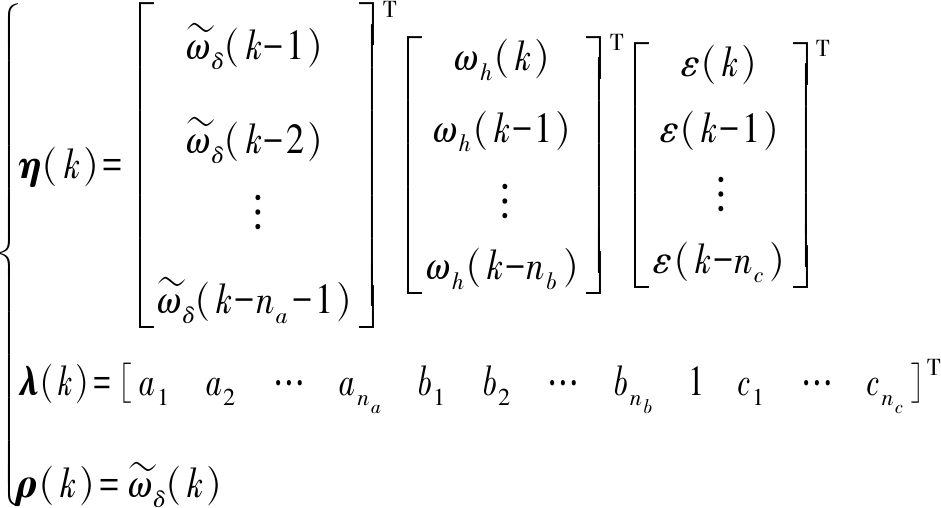
(14)
式中 η(k)——目标数据向量
λ(k)——需要被拟合的参数向量
ρ(k)——测量数据向量
拟合η(k)时需要计算模型建模产生的随机噪声ε(k),但随机噪声不容易被测量,所以在拟合过程中计算出ARMAX模型推算的转角速度估计值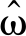h,δ和实际测量转角速度
之间的误差作为随机噪声,即
Erls(k)=ρ(k)-η(k-1)λ(k-1)
(15)
式中 Erls——建模数据中噪声
η(k-1)λ(k-1)——第k-1时刻转角速度预测值
ARMAX模型阶数过低时不能准确描述转向系统;阶数过高时会产生过拟合,导致预测值失真。本文采用贝叶斯信息准则(Bayesian information criterions, BIC)对模型进行定阶[29],BIC计算公式为
BIC=-2lnLsr+k1lnn1
(16)
式中 Lsr——似然函数
n1——样本数量
k1——需要估计的参数数量
用递归最小二乘法对ARMAX模型参数进行拟合辨识的算法伪代码为:
输入:转角速度序列
方向盘角速度序列ωh,样本数量n1
输出:ARMAX模型参数A(z)、B(z)、C(z)
(1)λout←0,BICmax←∞
(2)For na=1→8
(3)For nb=1→8
(4)For nc=1→8
(5)Krls=0,Γrls=0,k1=max([na nb nc])
/* 增益矩阵、协方差矩阵初始化 */
(6)While ‖λ(k1)-λ(k1-1)‖∞>ε
(7)计算Erls(k)、η(k)、ρ(k)
(9)λ(k1)=λ(k1-1)+Krls(k1)Erls(k1)
(10)Γrls(k1)=(I+Krls(k1)ηT(k1-1))Γrls(k1-1)
(11)k1=k1+1
(12)End while
(13)计算ωδ,h
(14)Lsr=σ2(ωδ,h-ρ) /* 计算似然函数 */
(15)计算BIC
(16)If BIC<BICmax
(17)BICmax=BIC,λout=λ(k1)
(18)End if
(19)End for
(20)End for
(21)End for
(22)Return λout
其中 Krls——RLS增益矩阵
Γrls——RLS协方差矩阵
λout——ARMAX模型参数
I——单位矩阵
拟合中需要用到测量转角速度和方向盘角速度,通过运动学转角对时间进行微分可以获得转角速度,但是角速度微分后存在较大的微分噪声,而ARMAX模型中的随机噪声项能够很好地将噪声进行拟合,从而达到无轮角传感器也能建立转向模型。通过前期试验,建立转向系统ARMAX模型参数为
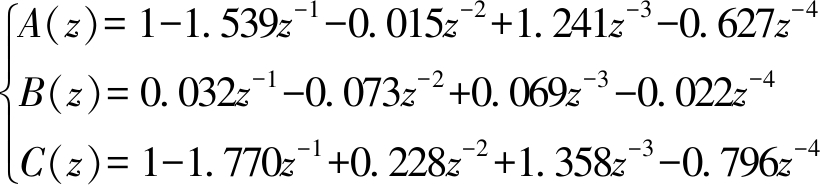
(17)
3 后轮轴中心接地点速度获取方法
双BDS-GNSS定位天线相对后轮轴中心接地点安装位置如图6所示。图6中,点A1为BDS-GNSS主天线位置;点A2为BDS-GNSS从天线位置;车辆载体坐标系Pxyz原点在点P(农机后轮轴中心接地点)上;l为点P和BDS-GNSS主天线之间的外形尺寸。后轮轴中心接地点和BDS-GNSS主天线存在杆臂矢量,在农机运动过程中,二者之间存在相对角运动,这两点观测速度存在杆臂效应误差[18-19]。本文通过对BDS-GNSS主天线测量的速度进行杆臂效应补偿得到后轮轴接地中心点速度。
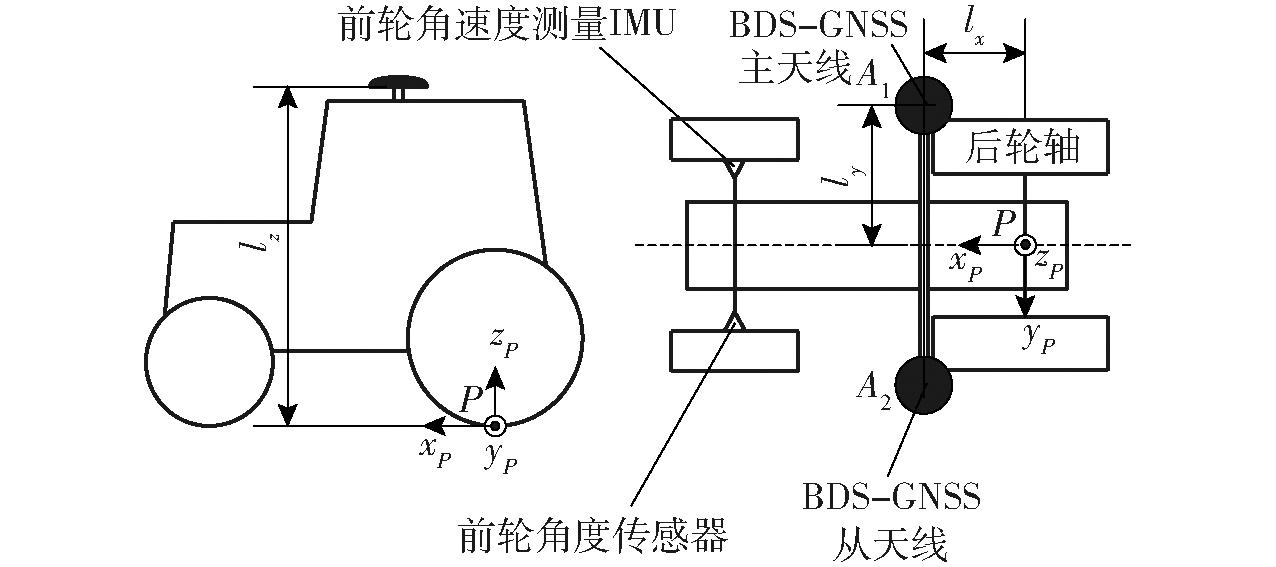
图6 GNSS天线杆臂示意图
Fig.6 Schematic of bar arm between GNSS antenna and center of rear bridge
车辆载体坐标系Pxyz原点在点P上,x轴沿车体纵轴指向前,y轴沿车体横轴指向左,z轴沿车体竖轴指向上,导航坐标系Nxyz符合东北天地理坐标系,从载体坐标系转到导航坐标系的旋转余弦矩阵
为
(18)
其中
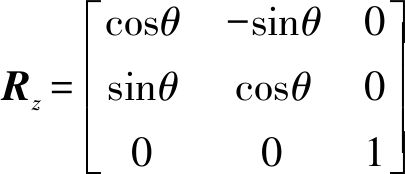
(19)
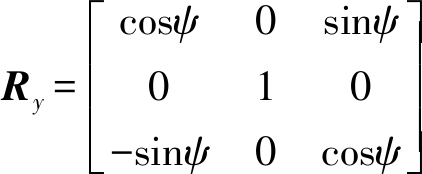
(20)
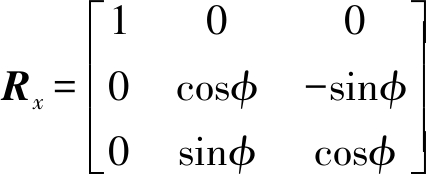
(21)
再根据哥氏定理可得
(22)
其中
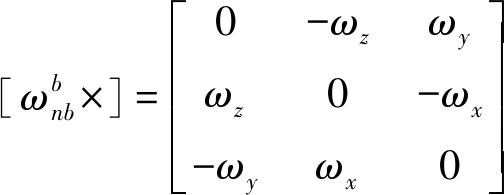
(23)
r=[lx ly lz]T
(24)
式中 
——BDS-GNSS主天线点A1相对于导航坐标系的三维速度
后轮轴中心接地点P相对于导航坐标系的三维速度
r——BDS-GNSS主天线点A1相对于后轮轴中心点P的杆臂矢量
拖拉机三轴角速度反对称矩阵
BDS-GNSS主天线点A1速度可以按照横摆角分解到正东和正北两个方向,即
=[vant,e vant,n vant,u]T≈
[vantcosθ vantsinθ 0]T
(25)
式中 vant,e、vant,n、vant,u——BDS-GNSS主天线东向、北向和天向运动速度
补偿后后轮轴中心接地点速度为
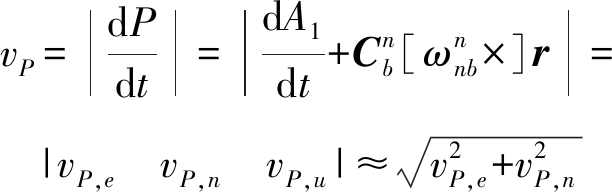
(26)
4 卡尔曼滤波器设计
设计一维的卡尔曼滤波器,定义滤波器的被估计状态量为前轮转角。方向盘角速度结合ARMAX模型预测出转角速度,前轮转角受方向盘角速度序列驱动,驱动激励状态方程为
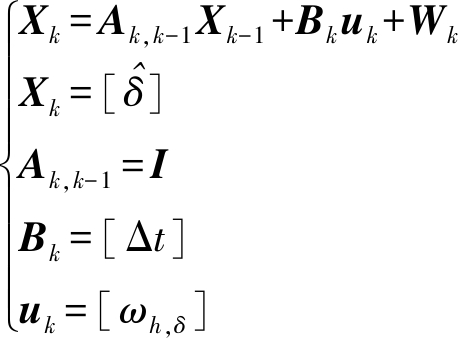
(27)
式中 Xk——第k时刻被估计状态
Ak,k-1——tk-1至tk时刻一步转移矩阵
Bk——控制驱动矩阵
Wk——方向盘角速度-转角速度系统模型噪声,服从正态分布
将式(26)的结果代入式(27)后获得运动学转角,以运动学转角作为量测更新,对状态向量估计进行修正,从而得到最优估计,提高模型估计精度。卡尔曼滤波器量测方程为
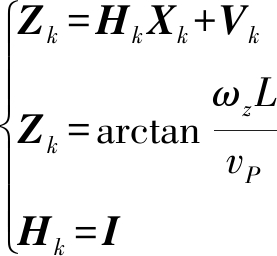
(28)
式中 Zk——可观测状态
Hk——量测矩阵
Vk——转角量测噪声,服从正态分布
由于拖拉机速度较低时运动学转角计算误差大,影响滤波器收敛,故对滤波器添加约束,当速度小于0.3 km/h时,滤波器不运作,估计值为0°;当速度大于0.3 km/h时,滤波器开始运作,卡尔曼增益和协方差矩阵开始收敛,估计结果趋于稳定。
针对本系统卡尔曼滤波器参数选取,CES-T型电动方向盘内置编码器分辨率为0.035°,试验拖拉机传动比为10.5,可以估算过程噪声为0.035°/10.5=0.003°。设计量测噪声标定试验,将方向盘分别打到左右极限并保持以车速1 km/h向前行驶,并以频率50 Hz记录拖拉机的运动学转角,求出2次平稳过程的运动学转角均值以及方差,标定试验场景如图7所示。标定试验结果如图8所示,试验得出,运动学转角左右标准差平均值为2.066°和2.216°,且运动学转角左右极限值为35.62°和-36.705°,求其两次结果平均值,可以估算运动学转角可观测时的观测噪声为2.143°,最后将状态方程和量测方程代入卡尔曼滤波器中进行估计。
图7 卡尔曼滤波器噪声误差标定试验
Fig.7 Calibration test of noise error of Kalman filter
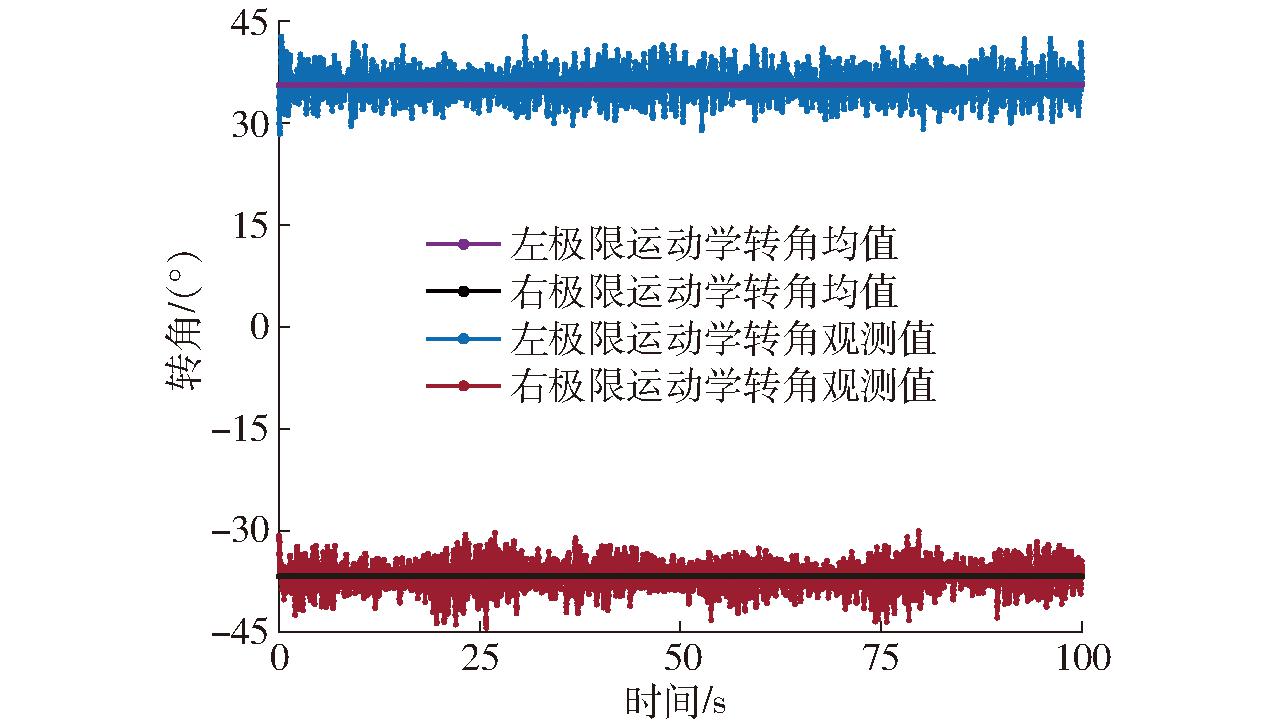
图8 卡尔曼滤波器噪声误差标定结果
Fig.8 Calibration result of noise error of Kalman filter
5 前轮转角估计测试试验
5.1 试验方法
为了评估拖拉机前轮转角估计方法性能和实用性,设计了速度测量方法验证试验、前轮转角动态测试试验和直线跟踪3组试验,对比不使用速度补偿或不使用ARMAX模型(取方向盘固定传动比为10.5)的结果。试验地点在华南农业大学增城试验基地的田块上,试验场地如图9所示。
图9 测试试验场地与测试中的拖拉机
Fig.9 Tractor under test and test site
5.2 速度测量方法验证试验
试验设计:保持固定的油门和挡位驾驶拖拉机,前轮角度传感器跟踪幅值为20°的方波信号,人工切换前轮转角方向,导航控制器以频率50 Hz保存带速度杆臂补偿与无速度杆臂补偿的运动学转角,和实际转角对比测量效果。
试验指标:BDS-GNSS主天线位置速度和拖拉机后轮轴中心接地点速度的标准差;带速度杆臂补偿与无速度杆臂补偿的运动学转角的绝对误差和标准差。
试验分析:速度测量方法验证试验结果如图10所示。试验结果表明,速度杆臂补偿前的运动学转角测量平均绝对误差为2.856°,标准差为2.523°;速度杆臂补偿后的运动学转角测量平均绝对误差为1.110°,标准差为1.727°,相比补偿前分别减少61.13%和31.55%;速度补偿前标准差为0.147 m/s,补偿后标准差为0.042 m/s,减少71.43%。
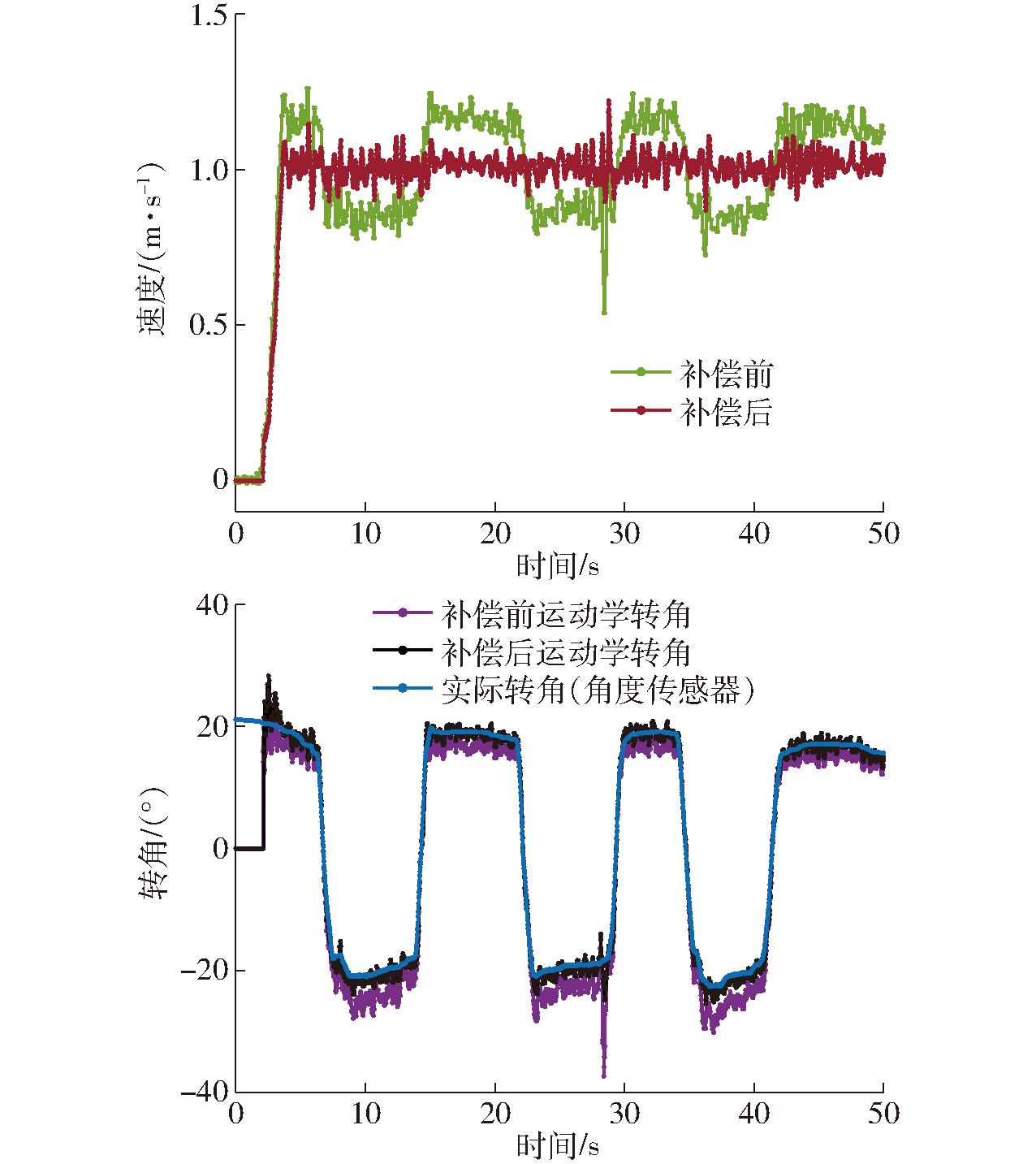
图10 速度补偿前后对比结果
Fig.10 Comparing results before and after compensation of velocity
5.3 前轮转角动态测试试验
试验设计:拖拉机保持固定油门和挡位(直线行驶速度为1 m/s),设定电动方向盘角速度以60、90、120、150°/s使前轮转角左右转向10°,控制器以频率50 Hz记录用ARMAX模型计算的转角速度预测值和基于ARMAX-KF的转角估计值、固定传动比计算的转角速度以及基于固定传动比和卡尔曼滤波器的转角估计值和运动学转角。
试验指标:前轮角度传感器测量的转角、前轮IMU测量的转角速度作为参考,对比在转角10°范围内的转角估计平均绝对误差、标准差,转角速度预测值的标准差。
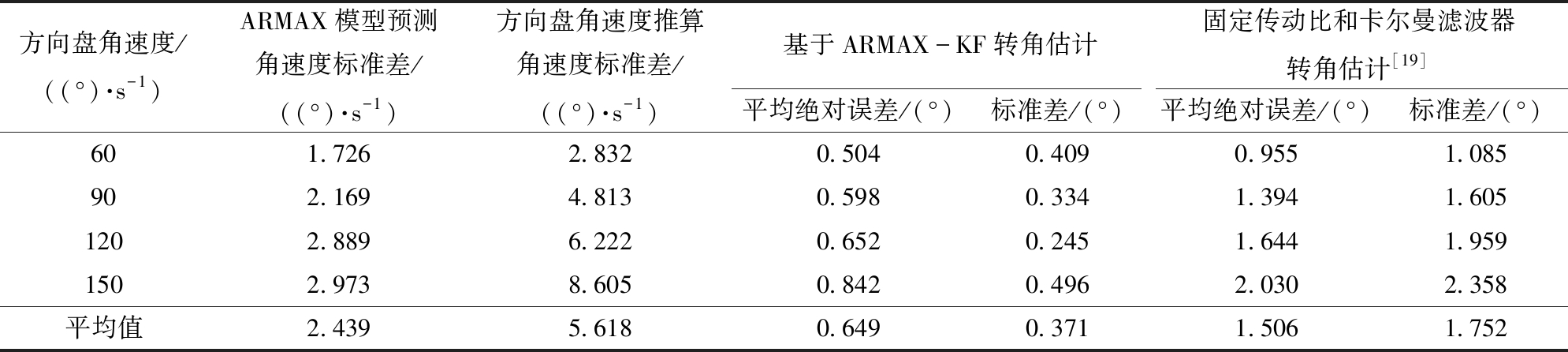
试验分析:方向盘不同角速度下的转角估计结果如图11所示;电动方向盘换向过程的转角速度预测结果如图12所示;性能对比如表1所示。由图11可知,当拖拉机刚启动时,运动学转角约束成0°,拖拉机达到设定速度阈值后,滤波器开始运作,估计误差开始减小;4组试验的性能对比结果表明,拖拉机在行驶过程中,方向盘在不同角速度下,通过ARMAX模型预测的转角速度标准差为2.439(°)/s,相比通过方向盘用固定传动比计算的转角速度标准差减少56.58%,基于ARMAX-KF的转角估计的平均绝对误差为0.649°,标准差为0.371°,相比采用固定传动比和卡尔曼滤波器的转角估计分别减少56.9%和78.82%。
表1 动态转角测试试验性能对比
Tab.1 Performance comparison of dynamic steering angle test
方向盘角速度/((°)·s-1)ARMAX模型预测角速度标准差/((°)·s-1)方向盘角速度推算角速度标准差/((°)·s-1)基于ARMAXKF转角估计固定传动比和卡尔曼滤波器转角估计[19]平均绝对误差/(°)标准差/(°)平均绝对误差/(°)标准差/(°)601.7262.8320.5040.4090.9551.085902.1694.8130.5980.3341.3941.6051202.8896.2220.6520.2451.6441.9591502.9738.6050.8420.4962.0302.358平均值2.4395.6180.6490.3711.5061.752
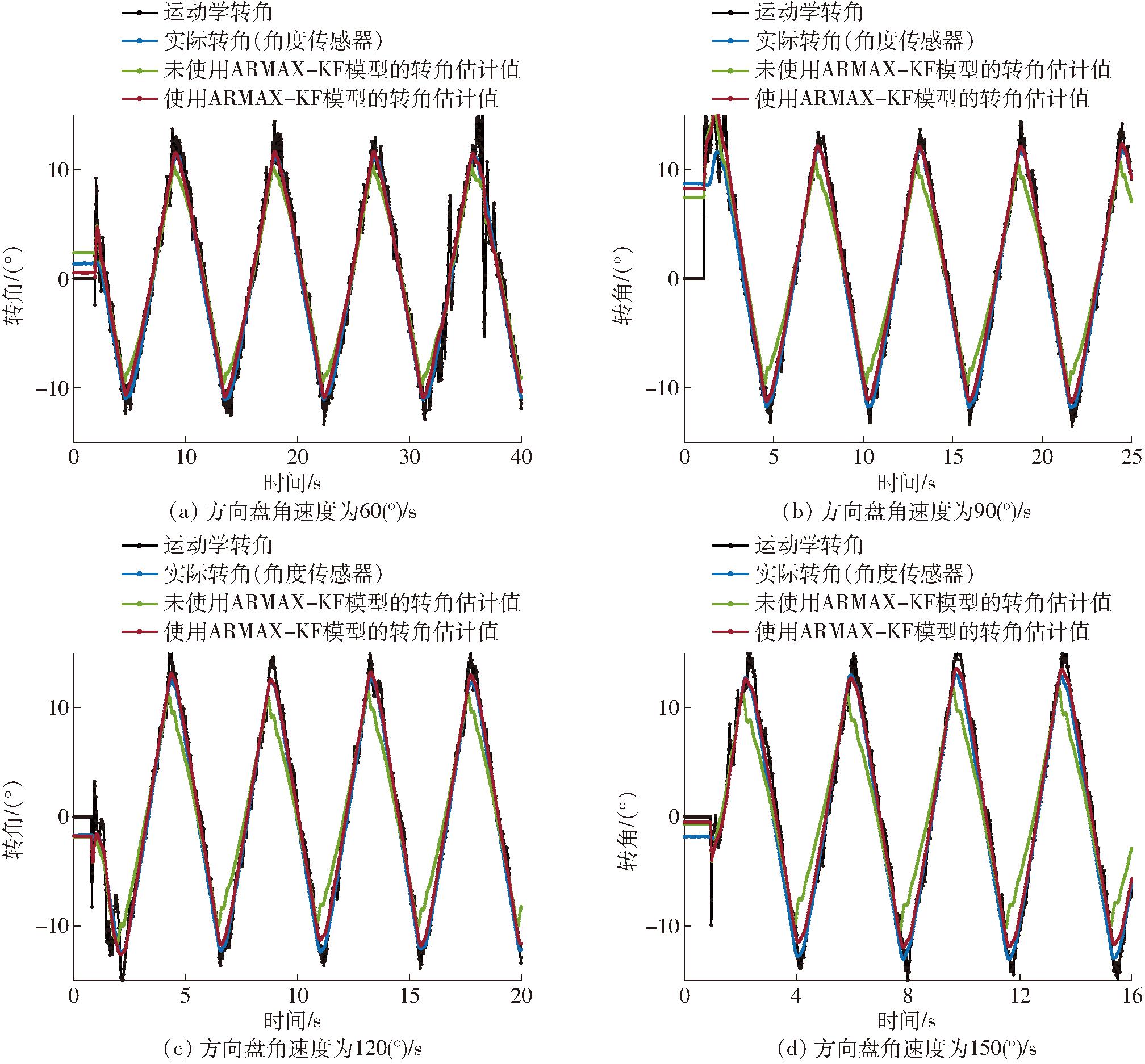
图11 前轮转角动态测试试验转角估计结果
Fig.11 Dynamic steering angle test results of steering angle estimation
图12 前轮转角动态测试试验角速度预测结果
Fig.12 Dynamic steering angle test results of angular velocity prediction of steering angle
由此看出采用固定传动比的转角估计结果在换向时会产生较大的估计误差,这是由于不考虑拖拉机转向系统的非线性部分导致的,由图12可以看出,实际转角速度相对于方向盘角速度存在相位滞后和阻尼,通过ARMAX模型可以辨识这个过程。
5.4 颠簸路面测试试验
试验设计:在水泥路面上规划直线路径,并在路径上铺设2种高度的减速带,减速带长、宽、高分别为500 mm×320 mm×50 mm、500 mm×320 mm×100 mm,拖拉机单边跨过减速带的过程中,横滚角产生的最大变化角度大于5°,试验场景如图13所示。拖拉机保持固定油门和挡位,拖拉机以行驶速度5 km/h进行直线跟踪,并采用ARMAX-KF和固定传动比估计的两种方法估计转角,试验进行 4组。
图13 减速带铺设的试验场景
Fig.13 Test scene of laying speed bumps
试验指标:前轮角度传感器测量的转角作为参考,对比基于ARMAX-KF以及采用固定传动比和卡尔曼滤波器的转角估计标准差。
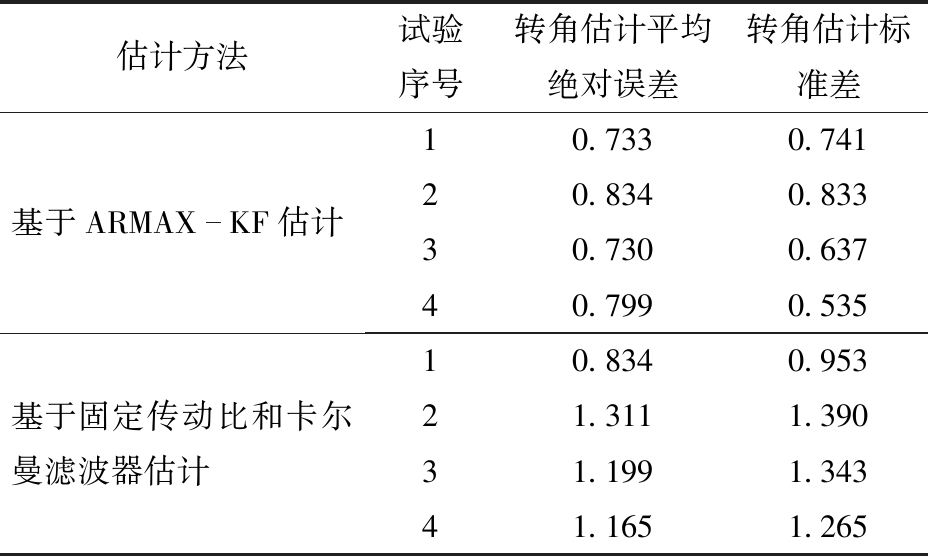
试验分析:其中第1组过减速带横滚角变化和转角估计结果如图14所示,4组的±5°颠簸路面试验结果统计如表2所示。试验结果表明,基于ARMAX-KF的转角估计平均标准差为0.687°,相比基于固定传动比和卡尔曼滤波器的转角估计平均标准差减少44.51%。
表2 颠簸路面测试试验结果
Tab.2 Results of bumpy road test (°)
估计方法试验序号转角估计平均绝对误差转角估计标准差基于ARMAXKF估计10.7330.74120.8340.83330.7300.63740.7990.535基于固定传动比和卡尔曼滤波器估计10.8340.95321.3111.39031.1991.34341.1651.265
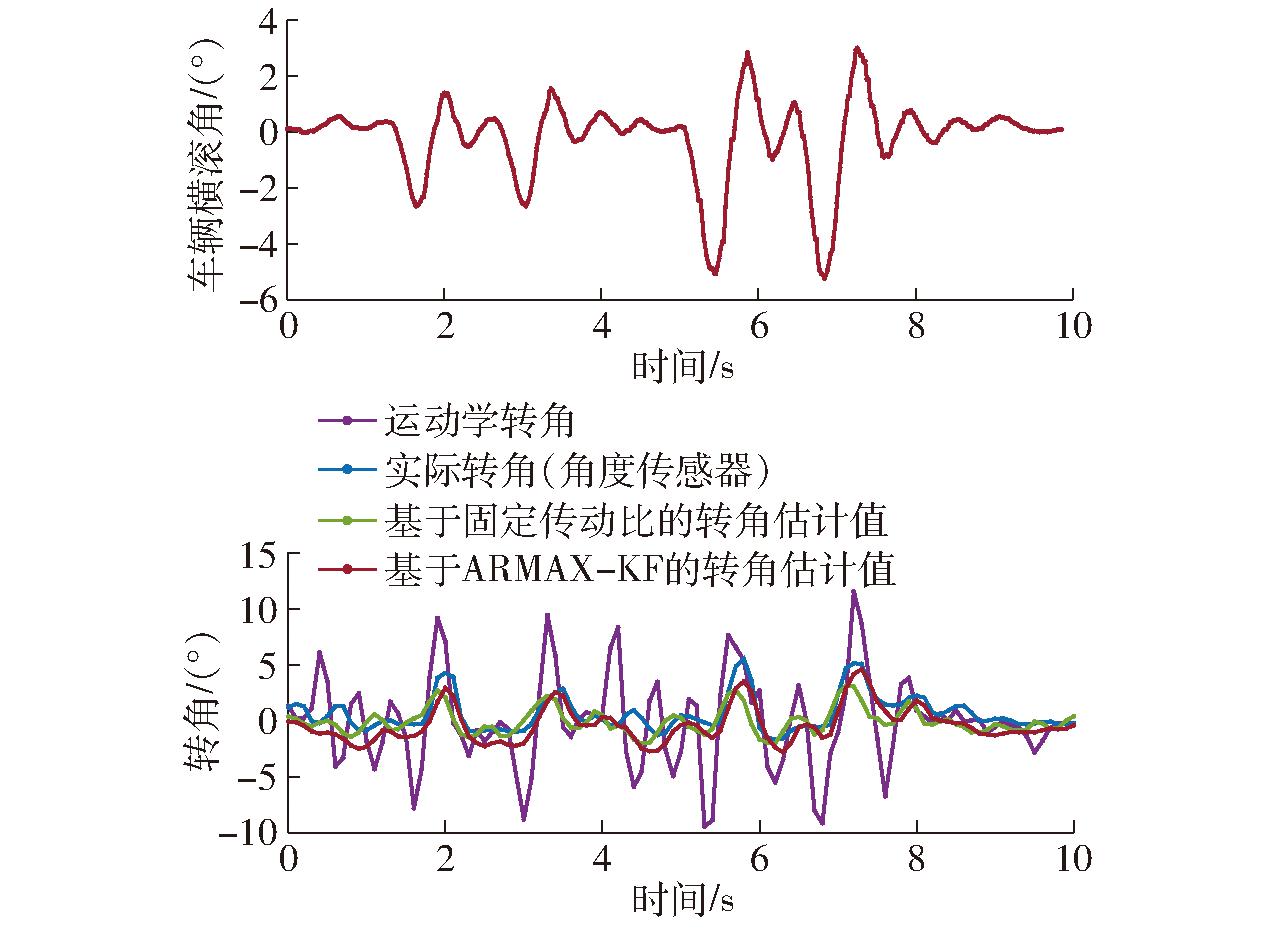
图14 第1组颠簸路面试验结果
Fig.14 Test results of the first set of bumpy road tests
5.5 直线导航跟踪测试试验
试验设计:规划直线路径后,保持固定油门和挡位使拖拉机直线行驶速度为3、5、7 km/h,试验时采用基于ARMAX-KF估计、基于固定传动比和卡尔曼滤波器估计和角度传感器的3种结果作为转角反馈用于转向控制,共进行9组直线导航跟踪测试试验,为对比不同转角估计方法的性能,采用ARMAX-KF估计的试验中,同时运行2种估计方法。控制器以频率10 Hz记录数据。
试验指标:前轮角度传感器测量的转角作为参考,对比基于ARMAX-KF以及采用固定传动比和卡尔曼滤波器的转角估计标准差;直线跟踪平均绝对横向偏差和横向偏差标准差。
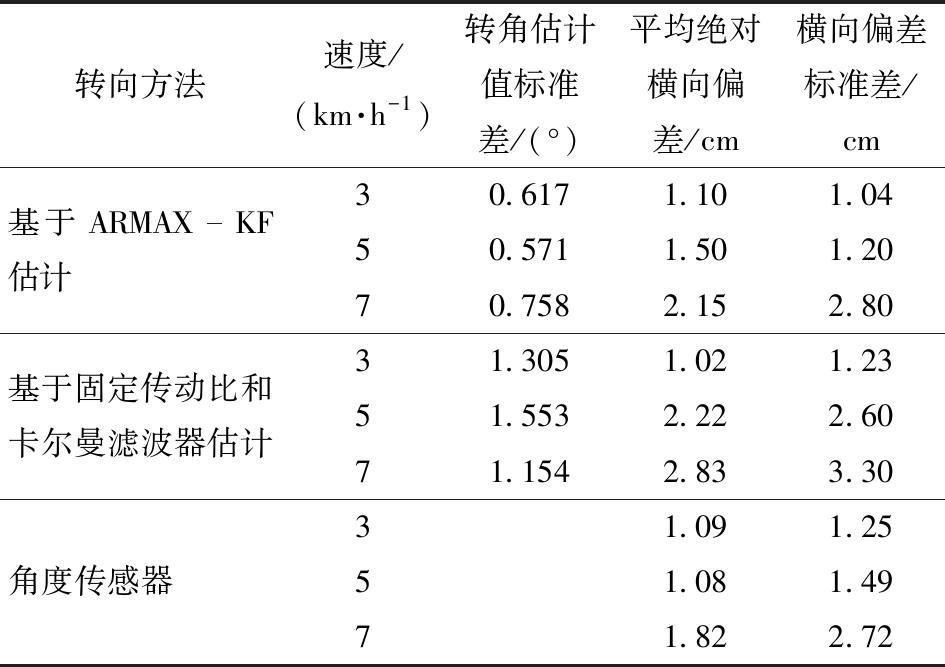
试验分析:试验统计结果如表3所示,其中拖拉机在速度5 km/h下的横向偏差结果如图15所示,拖拉机基于ARMAX-KF估计的直线跟踪转角估计结果如图16所示。基于ARMAX-KF估计和角度传感器试验的位置偏差标准差基本小于2.5 cm,满足拖拉机直线导航作业要求。其中采用固定传动比和卡尔曼滤波器的导航跟踪位置偏差较大,因为转角估计偏差存在滞后,导致控制效果差。
表3 直线导航跟踪测试横向偏差
Tab.3 Lateral error of linear navigation tracking test
转向方法速度/(km·h-1)转角估计值标准差/(°)平均绝对横向偏差/cm横向偏差标准差/cm基于ARMAXKF估计30.6171.101.0450.5711.501.2070.7582.152.80基于固定传动比和卡尔曼滤波器估计31.3051.021.2351.5532.222.6071.1542.833.30角度传感器31.091.2551.081.4971.822.72
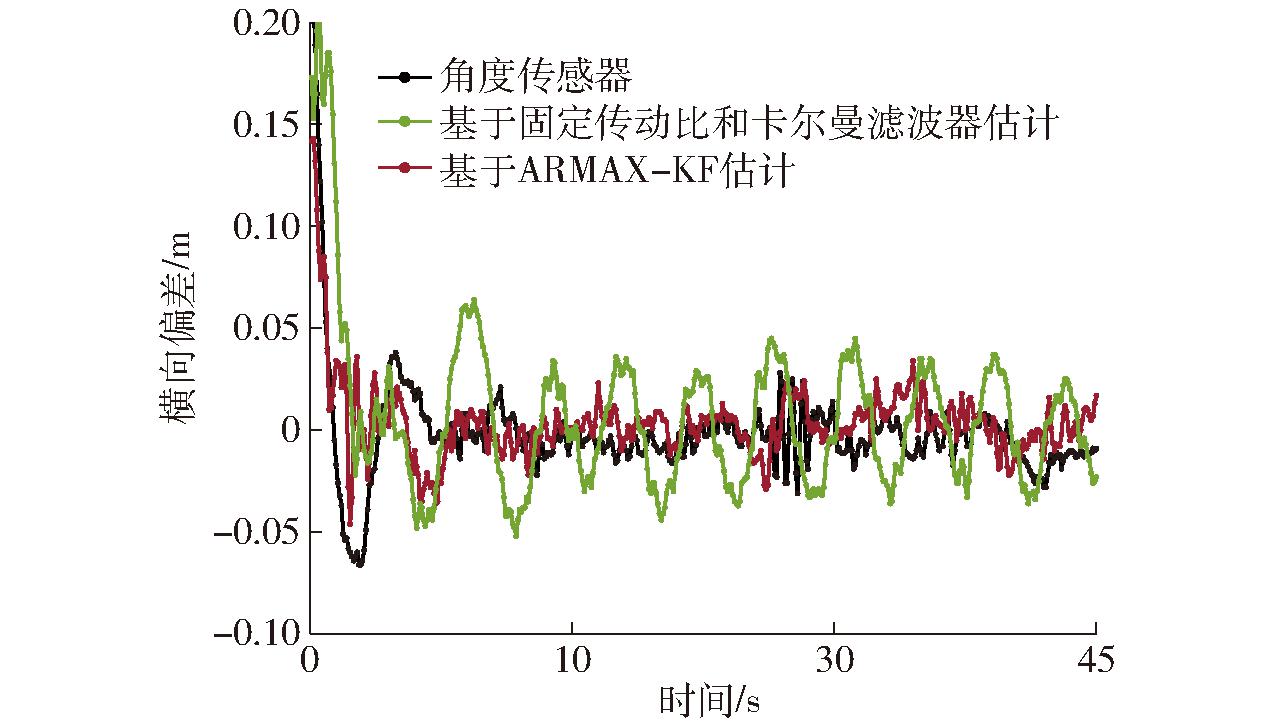
图15 5 km/h下直线导航跟踪的横向偏差变化曲线
Fig.15 Lateral error curves of linear navigation tracking at 5 km/h
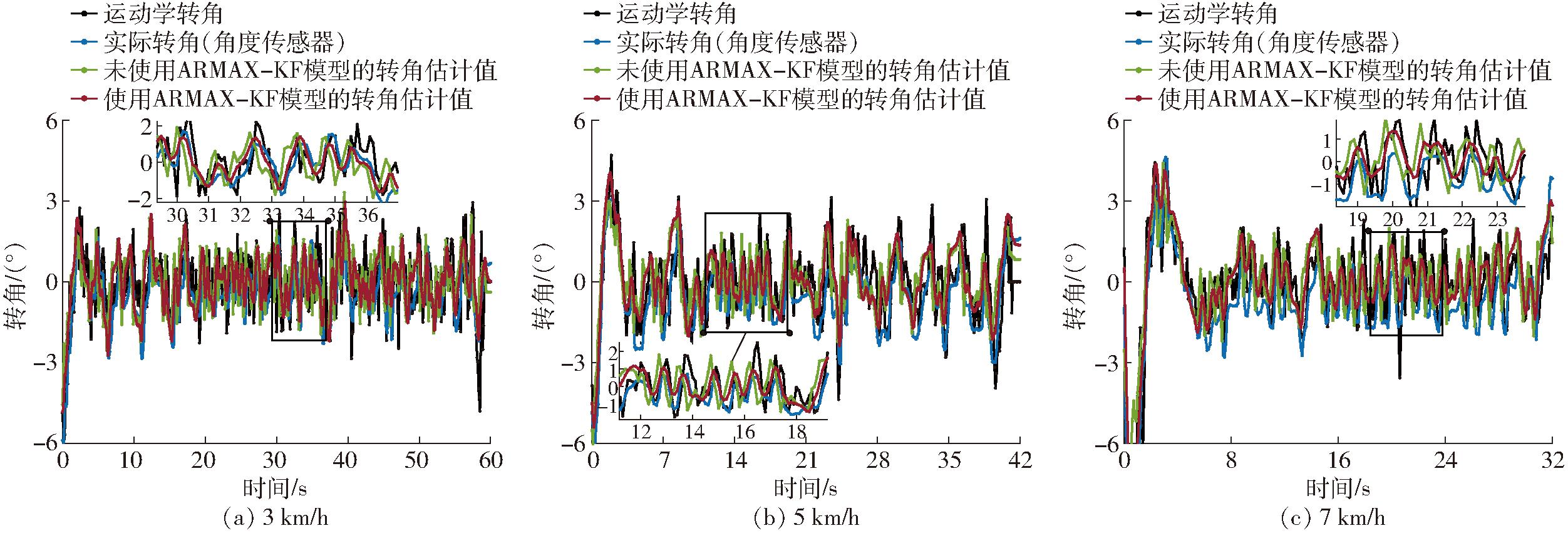
图16 基于ARMAX-KF的直线导航跟踪测试的转角估计结果
Fig.16 Angle estimation results of linear navigation tracking test based on ARMAX-KF
由表3可知,采用ARMAX-KF模型,速度3、5、7 km/h下的转角估计平均标准差为0.649°;相比采用固定传动比和卡尔曼滤波器的转角估计平均标准差减少42.97%,试验结果表明,采用ARMAX-KF模型显著提高了转角估计精度。
6 结论
(1)针对拖拉机的转向系统存在油隙、内泄、迟滞和死区等非线性特性,采用ARMAX模型对拖拉机的转向系统进行了系统辨识。通过动态转角测试试验,ARMAX模型预测的转角速度标准差为 2.439(°)/s,相比通过方向盘用固定传动比计算的转角速度标准差减少56.58%。
(2)根据拖拉机的运动学模型,提出了后轮轴中心接地点速度精确测量方法,试验结果表明,速度杆臂补偿后的运动学转角测量平均绝对误差为1.110°,标准差为1.727°,相比速度杆臂补偿前分别减少61.13%和31.55%。
(3)以运动学转角作为量测,设计了卡尔曼滤波器融合解算出转角估计值,动态测试试验的平均绝对误差为0.649°,标准差为0.371°,相比不采用ARMAX模型分别减少56.9%和78.82%;3种速度3、5、7 km/h下的直线导航跟踪试验结果平均标准差为0.649°,相比不采用ARMAX模型标准差减少42.97%。
[1] YAO Z, ZHAO C, ZHANG T. Agricultural machinery automatic navigation technology[J]. iScience, 2023, 27(2): 108714.
[2] 沈跃,张亚飞,刘慧,等.农业装备自动控制技术研究综述[J].农业机械学报,2023,54(8):1-18.SHEN Yue,ZHANG Yafei,LIU Hui,et al. Research review of agricultural equipment automatic control technology[J]. Transactions of the Chinese Society for Agricultural Machinery,2023,54(8):1-18.(in Chinese)
[3] 白学峰,常江雪,滕兆丽,等. 我国智能农业拖拉机关键技术研究进展[J]. 智能化农业装备学报(中英文), 2022,3(2):10-21.BAI Xuefeng,CHANG Jiangxue,TENG Zhaoli,et al. Research progress on key technologies of intelligent agricultural tractors in China[J]. Journal of Intelligent Agricultural Mechanization,2022,3(2):10-21. (in Chinese)
[4] 杨洋,张刚,查家翼,等.基于直流电机与全液压转向器直联的自动转向系统研究[J]. 农业机械学报,2020,51(8):44-54,61.YANG Yang, ZHANG Gang, ZHA Jiayi, et al. Design of automatic steering system based on direct connection of DC motor and full hydraulic steering gear[J]. Transactions of the Chinese Society for Agricultural Machinery, 2020,51(8):44-54,61. (in Chinese)
[5] 孟志军,王昊,付卫强,等. 农业装备自动驾驶技术研究现状与展望[J]. 农业机械学报, 2023,54(10):1-24.MENG Zhijun,WANG Hao,FU Weiqiang,et al. Research status and prospects of agricultural machinery autonomous driving[J]. Transactions of the Chinese Society for Agricultural Machinery,2023,54(10):1-24. (in Chinese)
[6] WANG L, ZHU S, LIU Y, et al. A novel path tracking method of tractor based on improved second-order sliding mode considering front wheel steering angle compensation[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2023, 237(9): 2205-2216.
[7] 何杰,朱金光,罗锡文,等. 电动方向盘插秧机转向控制系统设计[J]. 农业工程学报, 2019,35(6):10-17.HE Jie,ZHU Jingguang,LUO Xiwen,et al. Design of steering control system for rice transplanter equipped with steering wheel-like motor[J]. Transactions of the CSAE,2019,35(6):10-17. (in Chinese)
[8] NAGASAKA N, TAMAKI K, NISHIWAKI K, et al. A global positioning system guided automated rice transplanter[J]. IFAC Proceedings Volumes, 2013, 46(18): 41-46.
[9] 房素素,鲁植雄,王增才,等. 拖拉机线控液压转向系统设计及样车性能试验[J]. 农业工程学报, 2017,33(10):86-93.FANG Susu,LU Zhixiong,WANG Zengcai,et al. Design and prototype performance experiments of steering-by-wire hydraulic pressure system of tractor[J]. Transactions of the CSAE,2017,33(10):86-93. (in Chinese)
[10] 陈文良,谢斌,宋正河,等. 拖拉机电控液压动力转向系统的研究[J]. 农业工程学报, 2006,22(10):122-125.CHEN Wenliang,XIE Bin,SONG Zhenghe,et al. Electro-hydraulic power steering system for tractors[J]. Transactions of the CSAE,2006,22(10):122-125. (in Chinese)
[11] 胡书鹏,尚业华,刘卉,等. 拖拉机转向轮转角位移式和四连杆式间接测量方法对比试验[J]. 农业工程学报, 2017,33(4):76-82.HU Shupeng,SHANG Yehua,LIU Hui,et al. Comparative test between displacement and four-bar indirect measurement methods for tractor guide wheel angle[J]. Transactions of the CSAE,2017,33(4):76-82. (in Chinese)
[12] DONG Z, SONG Q, ZHANG W. Parameter optimization of tractor’s steering trapezoid mechanism based on improved adaptive direction strategy teaching-learning-based optimization[J]. Engenharia Agrícola, 2022, 42(4):e20220085.
[13] WU D, ZHANG Q, REID J F. Adaptive steering controller using a Kalman estimator for wheel-type agricultural tractors[J]. Robotica, 2001, 19(5): 527-533.
[14] 张智刚,黄海翔,罗锡文,等. 基于电动方向盘的拖拉机自动导航转向控制方法[J]. 农业工程学报, 2024,40(1):48-57.ZHANG Zhigang,HUANG Haixiang,LUO Xiwen,et al. Steering control system for a tractor using electric steering wheel[J]. Transactions of the CSAE,2024,40(1):48-57. (in Chinese)
[15] 张智刚,王桂民,罗锡文,等. 拖拉机自动驾驶转向轮角检测方法[J]. 农业机械学报, 2019,50(3):352-357.ZHANG Zhigang,WANG Guimin,LUO Xiwen,et al. Detection method of steering wheel angle for tractor automatic driving[J].Transactions of the Chinese Society for Agricultural Machinery,2019,50(3):352-357. (in Chinese)
[16] BREWER D E, WHITE G W, PEAKE J W. Vehicle gyro based steering assembly angle and angular rate sensor: US7477973B2[P]. 2009-01-13.
[17] WANG P, HU L, HE J, et al. Method for measuring the steering wheel angle of paddy field agricultural machinery by integrating RTK-GNSS and dual-MEMS gyroscope[J]. International Journal of Agricultural and Biological Engineering, 2022, 15(6): 197-205.
[18] 缪存孝,楚焕鑫,孙志辉,等.基于双GNSS天线及单陀螺的车轮转角测量系统[J].农业机械学报,2017,48(9):17-23.MIAO Cunxiao,CHU Huanxin,SUN Zhihui,et al. Wheel turning angle measurement system based on double GNSS antennas and single gyro[J]. Transactions of the Chinese Society for Agricultural Machinery,2017,48(9):17-23. (in Chinese)
[19] 陈云,何艳. 基于GNSS姿态与电机编码器的农机转向角度测量系统研制[J]. 农业工程学报, 2021,37(10):10-17.CHEN Yun, HE Yan. Development of agricultural machinery steering wheel angle measuring system based on GNSS attitude and motor encoder[J]. Transactions of the CSAE,2021,37(10):10-17.(in Chinese)
[20] HUANG X, WANG J. Identification of ground vehicle steering system backlash[J]. Journal of Dynamic Systems, Measurement, and Control, 2013, 135(1): 11014-11022.
[21] 何杰,满忠贤,胡炼,等. 履带式花生联合收获机路径跟踪控制方法与试验[J]. 农业工程学报, 2023,39(1):9-17.HE Jie,MAN Zhongxian,HU Lian,et al. Path tracking control method and experiments for the crawler-mounted peanut combine harvester[J]. Transactions of the CSAE,2023,39(1):9-17.(in Chinese)
[22] KHAN M A, BAIG D Z, ASHRAF B, et al. Dynamic modeling of a nonlinear two-wheeled robot using data-driven approach[J]. Processes, 2022, 10(3): 524.
[23] ZARDIN B, BORGHI M, GHERARDINI F, et al. Modelling and simulation of a hydrostatic steering system for agricultural tractors[J]. Energies, 2018, 11(1): 230.
[24] 王成志, 王云超. 运动副间隙及受力状态对空间转向机构转向误差的影响[J]. 机械工程学报, 2022, 58(4): 240-249.WANG Chengzhi, WANG Yunchao. Influence of clearances and force state of joints on steering error of spatial steering mechanism[J]. Journal of Mechanical Engineering, 2022, 58(4): 240-249.(in Chinese)
[25] KAYACAN E, KAYACAN E, RAMON H, et al. Nonlinear modeling and identification of an autonomous tractor-trailer system[J]. Computers and Electronics in Agriculture, 2014, 106: 1-10.
[26] MA L, LIU X. Recursive maximum likelihood method for the identification of Hammerstein ARMAX system[J]. Applied Mathematical Modelling, 2016, 40(13): 6523-6535.
[27] INOUE K, KUMAMARU K, INOUE H, et al. Identification and adaptive control of super heater system based on quasi-ARMAX model[J]. IFAC Proceedings Volumes, 2002, 35(1): 203-208.
[28] LUGNANI L, DOTTA D, LACKNER C, et al. ARMAX-based method for inertial constant estimation of generation units using synchrophasors[J]. Electric Power Systems Research, 2020, 180: 106097.
[29] 周平,刘记平. 基于数据驱动多输出ARMAX建模的高炉十字测温中心温度在线估计[J]. 自动化学报, 2018,44(3):552-561.ZHOU Ping,LIU Jiping. Data-driven multi-output ARMAX modeling for online estimation of central temperatures for cross temperature measuring in blast furnace ironmaking[J]. Acta Automatica Sinica,2018,44(3):552-561. (in Chinese)
[30] 李妍,毛志忠,王琰,等. 基于偏差补偿递推最小二乘的Hammerstein-Wiener模型辨识[J]. 自动化学报, 2010,36(1):163-168.LI Yan, MAO Zhizhong, WANG Yan,et al. Identification of Hammerstein-Wiener models based on bias compensation recursive least squares[J]. Acta Automatica Sinica,2010,36(1):163-168.(in Chinese)
