0 引言
中国是全球最大的棉籽生产国和消费国之一,棉籽产量和消费量均居世界前列[1]。棉籽主要下游产品为棉短绒、棉籽粕、棉壳、棉油等[2],在加工过程中需要使用齿辊式剥壳机对棉籽进行压缩破碎[3]。棉籽破碎过程对加工产品的品质有很大影响[4]:剥壳过程中,机构剪切力过大,导致棉仁粉碎破坏率增加,造成油脂分解和棉酚色素变性;加热过程中,由于棉籽破碎不全,造成棉籽粕粗蛋白含量较低,降低了其利用价值,且对人畜有害[5]。采用常规手段研究棉籽加工过程其物料特性的关键指标变化规律难度较大,采用数值模拟技术,可以对棉籽破碎过程进行深入研究,从而为优化现有棉籽剥壳机核心结构和关键工作参数提供依据。
离散元法作为用于分析颗粒破碎的重要方法,能够实现对不同材料类型、尺寸形状、负载条件以及设备结构的颗粒破碎模拟,已广泛应用于玉米[7-8]、颗粒饲料[9]、秸秆[10-11]、肥料[12]等农业物料中,但使用离散元法对棉籽物料破碎过程进行研究鲜见报道。
目前在研究农业物料的破碎过程中,常使用粘结模型,子颗粒形状为球形颗粒聚合体[13],与实际情况相差较大。Tavares破碎模型是一种颗粒替换模型,目前在矿石破碎领域有着广泛应用[14]。与粘结模型相比Tavares破碎模型在模拟颗粒破碎过程时,子颗粒形状均为多面体,可以较好地描述颗粒破碎情况[15]。因此, Tavares破碎模型对剥壳机粉碎过程的模拟更为适合,可用于解析农业物料破碎过程和粉碎机理等问题。
为保证离散元标定的准确性,需要建立精确的颗粒模型,但目前对颗粒建模常常将真实颗粒简化为简单几何体[16],或者使用三维扫描技术获取颗粒轮廓,然后使用微粒填充轮廓,完成颗粒建模[17]。然而,棉籽颗粒形状较为复杂无法简化为简单几何体,使用颗粒填充法往往会导致计算时间过长。考虑到棉籽实际形状,将棉籽简化为凸多面体颗粒能够较好体现其特征。但由于多面体颗粒模型和多球聚合模型之间的几何形状差异,有必要在模拟中对其种间接触参数进行重新标定。
本文以棉籽为研究对象,通过三维扫描技术,运用网格简化法构建多面体棉籽模型;通过堆积角试验,完成多面体棉籽模型接触参数标定并进行验证;通过单颗粒压缩试验,完成Tavares模型参数标定,对比破碎力和破碎能实际值与仿真值,以验证参数准确性。
1 材料与模型
1.1 试验样品
选用新陆早84号脱绒棉籽为试验材料,原料来源为新疆维吾尔自治区石河子市北泉镇轧花厂。随机选取1 000粒棉籽,将其平均分为5组,通过排水法测得棉籽平均密度为954 kg/m3。随机选取500粒棉籽,将其平均分为5组,通过干燥法测得棉籽平均含水率为8.1%。
选取200粒棉籽,确定颗粒尺寸分布情况,使用数显游标卡尺(精度0.01 mm)测量棉籽长度、宽度和厚度(图1)。统计测量结果显示棉籽长度、宽度和厚度均符合正态分布,其标准值和标准差分别为(9.32±0.48) mm、(5.01±0.27) mm、(4.56±0.33) mm。
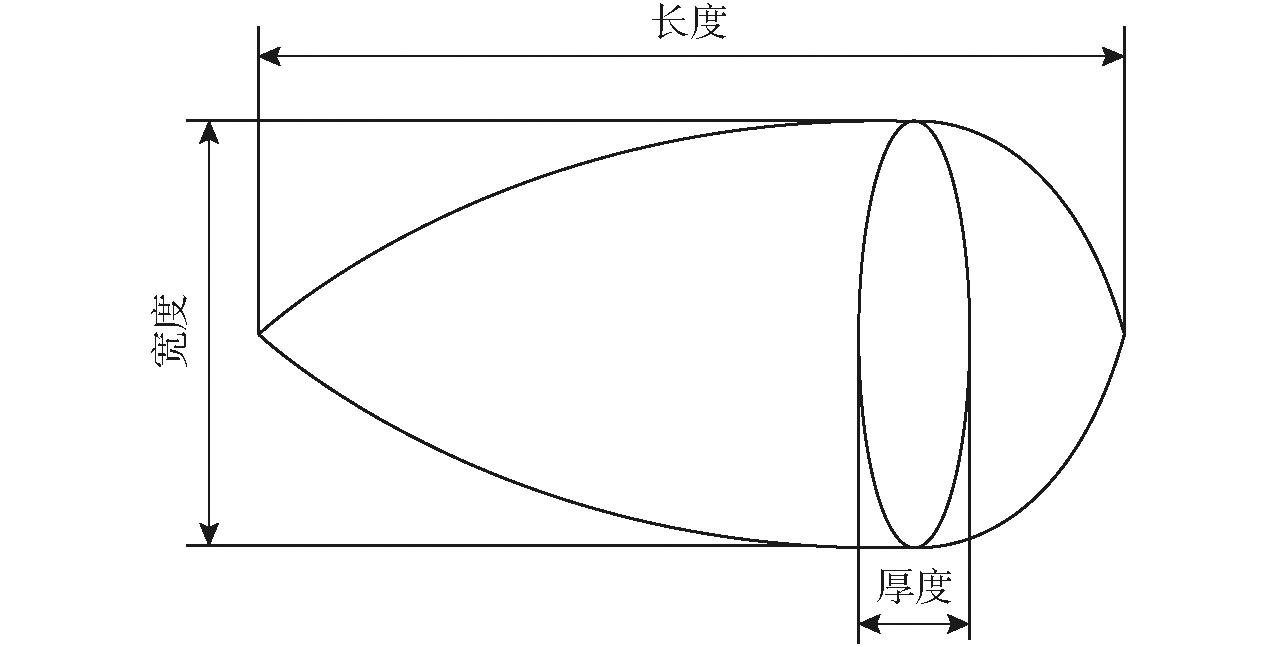
图1 棉籽三轴尺寸
Fig.1 Cottonseed triaxial dimensions
借助棉籽三维模型建立其离散元模型后,还需设置棉籽体积分布规律。实际棉籽体积测量困难,可借助棉籽三轴尺寸计算分析出棉籽体积[18]。棉籽体积计算公式为
(1)
式中 V——棉籽体积,mm3
L——棉籽长度,mm
W——棉籽宽度,mm
T——棉籽厚度,mm
由于测量得到的棉籽宽度与厚度较为相近,因此通过垂直长度方向的平均粒度G来计算棉籽体积,其计算公式为
(2)
其中
(3)
计算得到棉籽体积分布规律如图2所示,棉籽体积服从正态分布,由式(1)和式(2)计算的体积标准值和标准差分别为(75.15±9.43) mm3、(75.48±9.34) mm3。两者误差较小,证明使用平均粒度G来表示棉籽垂直长度方向的尺寸可靠。统计平均粒度G尺寸分布情况,将棉籽分为4.1～4.4 mm、4.4～4.7 mm、4.7～5.0 mm、5.0～5.3 mm 4个范围,为后续试验做准备。
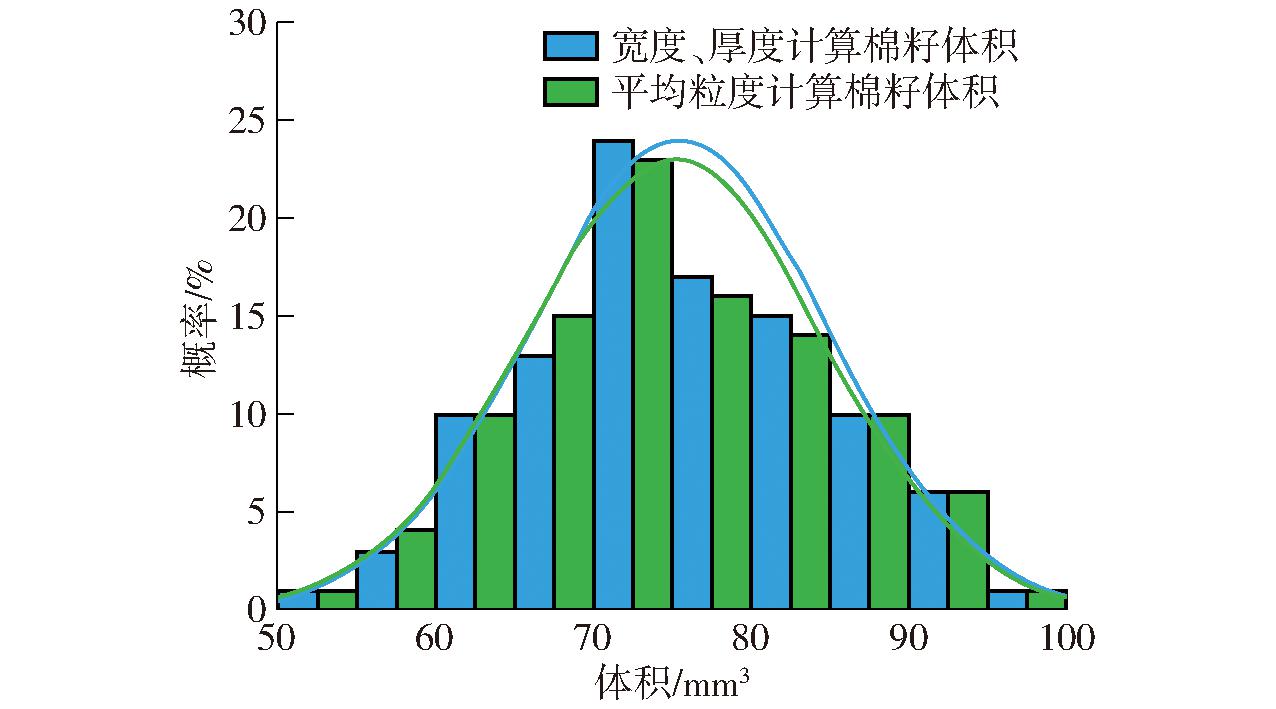
图2 棉籽体积分布
Fig.2 Volume distribution of cottonseed
1.2 Tavares模型
针对棉籽破碎过程,选用Rocky DEM中的Tavares 破碎模型进行仿真。Tavares破碎模型是一种颗粒替换模型,能够模拟颗粒在不同强度的应力作用下的瞬时破碎[19]。如图3所示,在对母颗粒施加外力达到破碎临界点时,母颗粒将被多个不同尺寸的子颗粒替换,随后破碎。
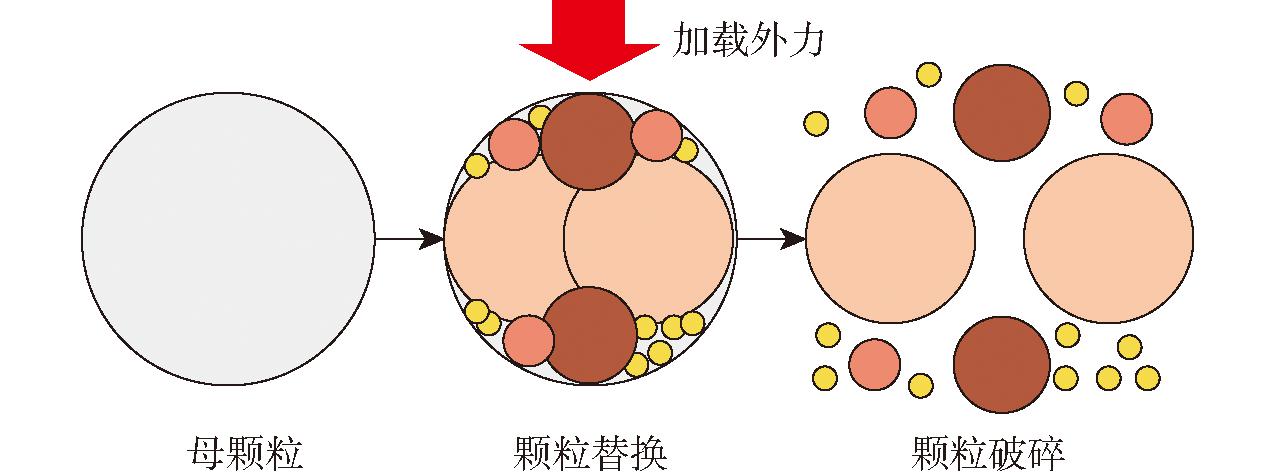
图3 Tavares模型破碎过程
Fig.3 Tavares model crushing process
在数量有限的试验样本中,棉籽颗粒破碎概率P可以通过样本中破碎比能E的排序,使用概率估算因子来进行计算。其计算公式为
(4)
式中 i——任意颗粒在试验样本中颗粒破碎比能升序排列中的序号
N——试验样本数量
Tavares破碎模型中,破碎概率P基于破碎比能E对数正态分布[20]。其计算公式为
(5)
其中
(6)
式中 E——棉籽颗粒破碎比能,J/kg
E50——棉籽颗粒破碎比能中值(50%概率发生破碎对应的破碎比能),J/kg
σ——棉籽颗粒破碎概率对数正态分布标准差
Emax——棉籽颗粒最大颗粒破碎比能,J/kg
棉籽颗粒最大颗粒破碎比能Emax通常被认为是棉籽颗粒破碎比能中值E50的10倍。棉籽颗粒破碎比能E与颗粒尺寸密切相关,其中破碎比能中值E50与颗粒尺寸之间关系式为
(7)
式中 E∞——棉籽颗粒剩余破碎比能,J/kg
d0——材料微观结构特征尺寸,mm
φ——破碎比能中值对粒度的幂律函数
式(7)中的E∞、d0、φ为试验数据进行仿真拟合出的模型参数。Tavares破碎模型认为,在颗粒尚未破碎的加载过程中,由于加载时产生的能量在颗粒中累积,导致颗粒损伤,从而使颗粒破碎比能E减小[21]。加载过程中,颗粒损伤率与接触表面刚度、颗粒体积、瞬时冲击比能有关。每进行一次未导致颗粒破碎加载,新的颗粒破碎比能需通过上一次的颗粒破碎比能和损伤率来计算,其表达式为
En=En-1(1-Dn)
(8)
其中
(9)
式中 En——第n次未导致棉籽颗粒破碎的加载后颗粒破碎比能,J/kg
Dn——第n次未导致棉籽颗粒破碎的加载过程中颗粒损伤率
γ——损伤累计系数
Et——第n次未导致棉籽颗粒破碎的加载过程中产生的瞬时破碎比能,J/kg
当Et大于En-1时,棉籽颗粒将根据Laguerre-Voronoi算法破碎并生成子颗粒[21]。将此时Et记为EB,子颗粒尺寸与EB的关系为
(10)
式中 t10——粒径小于棉籽1/10的子颗粒质量之和占棉籽质量的百分比
EBt——颗粒破碎比能量度,J/kg
A和b′是由试验拟合的模型参数,两者的乘积可表示颗粒破碎适应性,乘积越大,颗粒越软[19]。在Tavares破碎模型中,EBt通常由EB或E50来表示,Rocky DEM内默认选择为EB。
子颗粒尺寸和数量由子颗粒最小尺寸dmin和最小尺寸比
来决定。当子颗粒尺寸小于dmin和与子颗粒尺寸乘积两者中的最大值时,为保证仿真效率、提高准确率,将限制子颗粒进入计算域。通常在颗粒破碎仿真中需根据实际情况定义dmin,其余参数保持默认值。本文将通过棉籽单颗粒压缩试验对上述参数进行标定。
2 多面体棉籽模型构建与接触参数标定
2.1 多面体棉籽模型构建
离散元模型构建是离散元仿真的重要部分,离散元模型与实际物料模型近似程度越高,仿真准确性也越好。目前常使用三维扫描技术以准确获取物料表面特征[22],将其转换为由多个球体或平面组成的几何体。但棉籽颗粒形状较为复杂无法简化为简单几何体,使用颗粒填充法会导致计算时间过长。考虑到棉籽实际形状,将棉籽简化为由多个三角形平面组成的凸多面体颗粒能够较好体现其特征。
通过三维扫描技术获取棉籽轮廓模型,使用软件缩减模型分面数量,构建多面体棉籽离散元模型。具体步骤为:①选取尺寸接近平均值的棉籽,使用扫描仪扫描棉籽轮廓,获取棉籽点云数据。②使用软件对点云数据进行处理后得到棉籽轮廓模型。③将棉籽轮廓模型导入Solidworks 2022软件,使用网格建模功能对棉籽模型进行分面缩减,导出STL格式的多面体棉籽模型文件。
将多面体棉籽模型导入Rocky DEM中进行预试验时发现,不同分面数量的棉籽离散元模型在体积和仿真时间上存在差异。考虑到建模准确性和仿真效率,如图4所示,将模型分面数量分别设定为1 830、1 464、1 098、732、366,探究不同分面数量对模型准确性和仿真效率的影响,在保证模型准确的条件下提高仿真效率。
图4 棉籽轮廓模型及不同分面数棉籽模型
Fig.4 Cottonseed contour model and cottonseed models with different numbers of facets
将棉籽模型导入Rocky DEM软件中,利用文献[23]中参数进行堆积角预试验,工作站处理器型号Intel(R)Xeon(R) Gold 623,数值软化因子选择0.05,步长为1.5×10-5 s,根据前期试验,棉籽在3 s内静止,形成堆积角,故将时长设定为3 s。将试验结果导入Origin软件中绘制图像,如图5所示,随着棉籽模型分面数量增加,体积相对误差减小,且折线斜率不断减小;仿真时间随分面数量增加而增加,但其折线斜率较稳定。综合考虑仿真效率和准确性,选择分面数量为1 098的多面体棉籽模型用于后续仿真研究,对应的仿真时间为171 min,体积相对误差为0.46%。
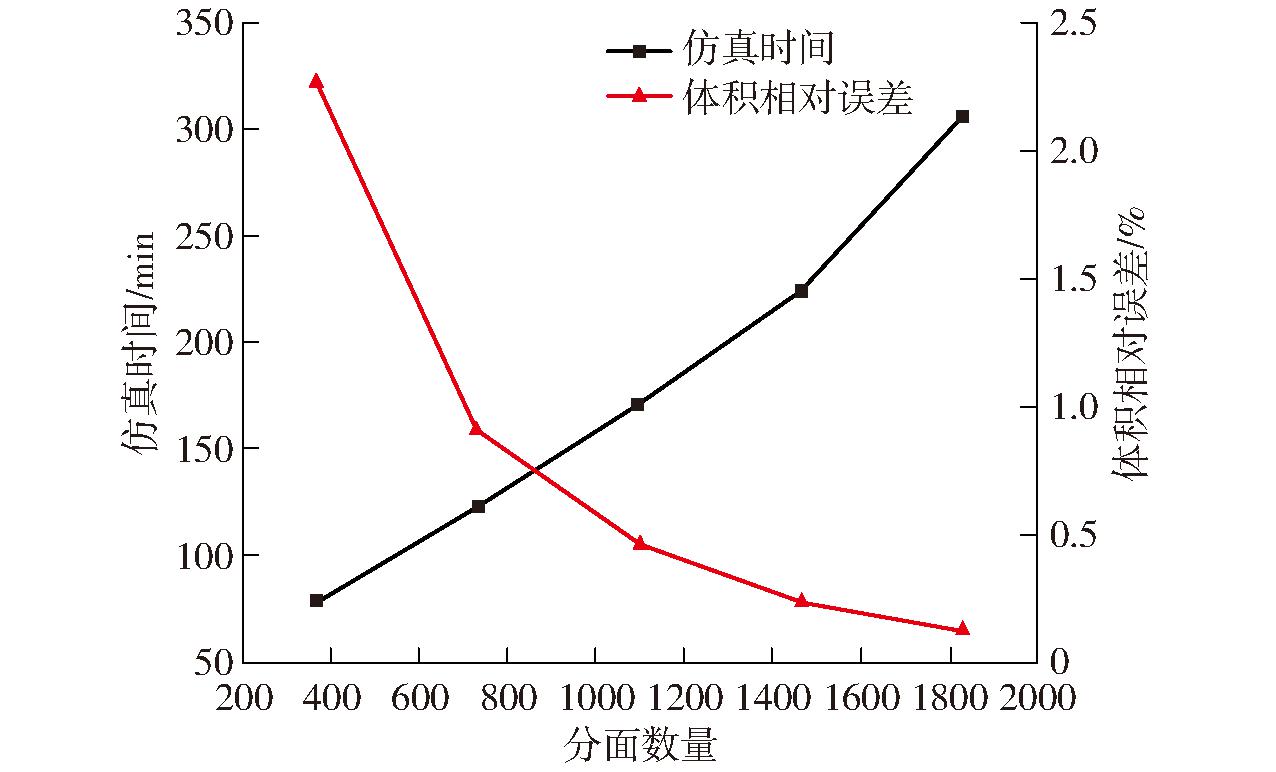
图5 不同分面数量时的棉籽模型体积相对误差及仿真时间
Fig.5 Comparison of simulation time, relative error, and number of facets for cottonseed model
2.2 棉籽接触参数标定
2.2.1 实际堆积角试验
通过物理试验与仿真试验结合的方式,使用圆筒提升法对棉籽种间参数进行标定。试验时将100 g棉籽放入内径50 mm的空心圆柱体中,以恒定速度0.05 m/s将圆筒提起,形成堆积角。使用相机获取堆积角图像,导入Matlab进行去噪、灰度、二值化等处理后提取图像边界进行线性拟合[24],拟合直线与水平面夹角即为实际堆积角(图6)。由于棉籽实际堆积角在两侧存在不同,为减少误差试验时分别测定两侧堆积角,取其平均值作为棉籽实际堆积角。进行10次重复试验获取平均值,得到圆筒提升法形成堆积角为24.73°。
图6 棉籽堆积角图像处理结果
Fig.6 Image processing results of cottonseed stacking angle
2.2.2 Rocky DEM堆积角仿真试验
棉籽种间参数难以通过实际试验获取准确值,因此需通过仿真标定来确定,其余参数参照文献[25],如表1所示。
表1 堆积角仿真参数设置
Tab.1 Stacking angle simulation parameters settings
参数数值棉籽泊松比0.19棉籽弹性模量/MPa33.796棉籽与钢板碰撞恢复系数0.46棉籽与钢板静摩擦因数0.51棉籽与钢板滚动摩擦因数0.21
取棉籽-棉籽碰撞恢复系数F1、棉籽-棉籽静摩擦因数F2、棉籽-棉籽滚动摩擦因数F3初始值为0.05、0.15、0.05,步长设置为0.05、0.05、0.05进行最陡爬坡试验。试验设计与结果如表2所示。根据最陡爬坡试验结果,选取2号、3号水平为低、高水平进行响应面试验,F1、F2、F3零水平为0.125、0.225、0.125。
表2 最陡爬坡试验设计方案及仿真结果
Tab.2 Design scheme and simulation test results of the steepest climbing test
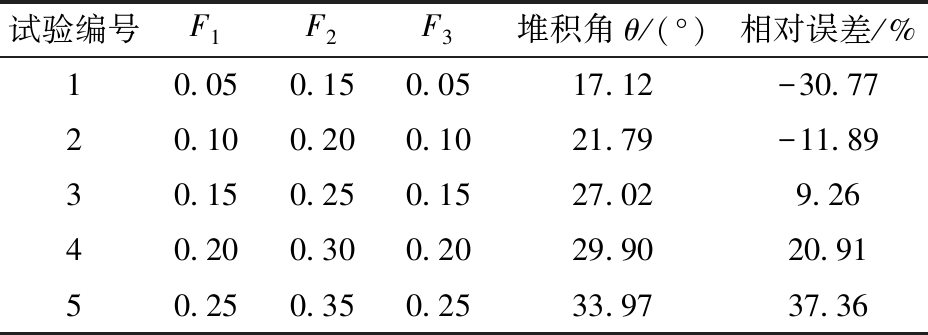
试验编号F1F2F3堆积角θ/(°)相对误差/%10.050.150.0517.12-30.7720.100.200.1021.79-11.8930.150.250.1527.029.2640.200.300.2029.9020.9150.250.350.2533.9737.36
通过Design-Expert软件进行三因素三水平响应面试验设计,中心水平设置5组重复试验,共进行17组棉籽堆积角仿真试验。试验设计与结果如表3所示,方差分析结果如表4所示。
表3 响应面试验设计方案及仿真结果
Tab.3 Response surface experimental design scheme and simulation results
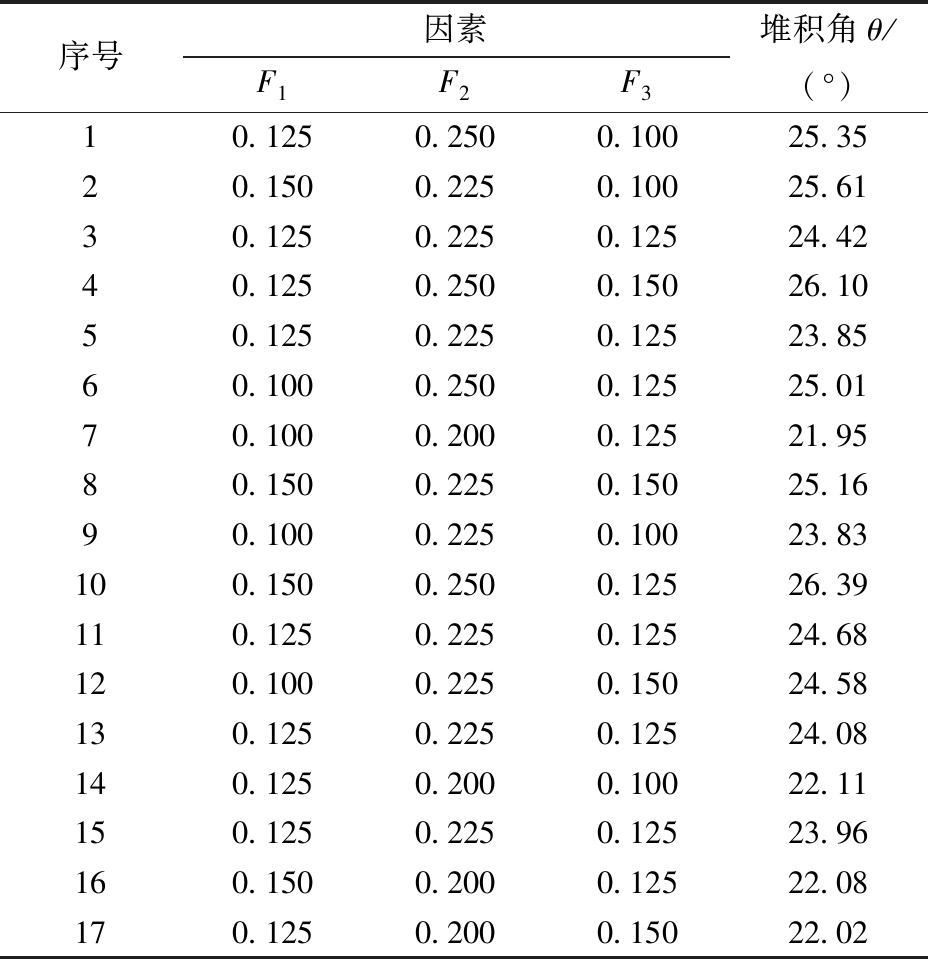
序号因素F1F2F3堆积角θ/(°)10.1250.2500.10025.3520.1500.2250.10025.6130.1250.2250.12524.4240.1250.2500.15026.1050.1250.2250.12523.8560.1000.2500.12525.0170.1000.2000.12521.9580.1500.2250.15025.1690.1000.2250.10023.83100.1500.2500.12526.39110.1250.2250.12524.68120.1000.2250.15024.58130.1250.2250.12524.08140.1250.2000.10022.11150.1250.2250.12523.96160.1500.2000.12522.08170.1250.2000.15022.02
表4 响应面试验方差分析
Tab.4 Analysis of variance in response surface methodology
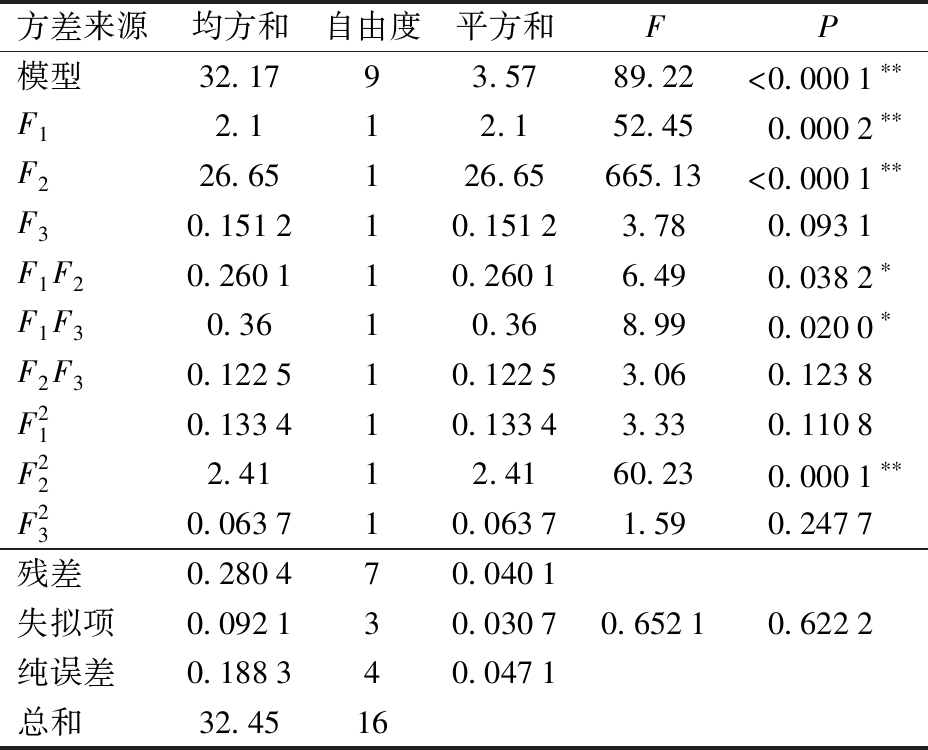
注:**表示影响极显著(P<0.01);*表示影响显著(P<0.05)。
方差来源均方和自由度平方和FP模型32.1793.5789.22<0.0001∗∗F12.112.152.450.0002∗∗F226.65126.65665.13<0.0001∗∗F30.151210.15123.780.0931F1F20.260110.26016.490.0382∗F1F30.3610.368.990.0200∗F2F30.122510.12253.060.1238F210.133410.13343.330.1108F222.4112.4160.230.0001∗∗F230.063710.06371.590.2477残差0.280470.0401失拟项0.092130.03070.65210.6222纯误差0.188340.0471总和32.4516
由表4可知,在棉籽堆积角试验中,F1、F2对棉籽堆积角影响极显著,F3对棉籽堆积角影响不显著;交互项中,F1F2、F1F3对棉籽堆积角影响显著,F2F3对棉籽堆积角影响不显著;二次项中,
对棉籽堆积角影响极显著,
对棉籽堆积角影响不显著。回归模型P值小于0.05,回归模型显著且失拟项P值大于0.05,失拟项不显著,回归有效。方差分析显示,棉籽多面体模型与多球聚合模型的显著影响因素较为相似[23],F1、F2均对其堆积角有显著影响。
为准确求得各因素最优参数组合,根据方差分析结果,建立棉籽堆积角二阶回归方程为
θ=-37.123-82.5F1+532.4F2-46.7F3+
(11)
利用Design-Expert软件进行优化求解,得到F1、F2、F3分别为0.106、0.248、0.105时,棉籽堆积角为24.73°。对优化求解得到的参数组合进行仿真验证,如图7所示,得到仿真堆积角为24.66°,与真实值的相对误差为0.28%,表明接触参数真实有效,可用于后续Tavares模型破碎试验中。
图7 棉籽实际堆积角与仿真堆积角对比
Fig.7 Comparison of actual and simulated stacking angles of cottonseed
3 Tavares破碎参数标定与验证
3.1 单颗粒压缩试验
在Tavares模型中,可以通过压缩颗粒进行单颗粒破碎试验,获取物料压力-位移曲线、破碎力及破碎比能,对各破碎参数进行拟合标定。
为使破碎参数具有代表性,选取平均粒度为4.1～4.4 mm、4.4～4.7 mm、4.7～5.0 mm、5.0～5.3 mm的4组棉籽颗粒进行单颗粒压缩试验(图8)。每组选取20个表面完整的棉籽颗粒,使用万能试验机进行单颗粒压缩试验,以获取棉籽颗粒加载后压力-位移曲线。试验时,使用电子天平称量棉籽质量,随后将棉籽置于万能试验机的承压板上,沿垂直长度方向进行加载,压缩头加载速率设为1 cm/min,触发力为0.3 N,实现准静态压缩。
图8 棉籽压缩试验
Fig.8 Cottonseed compression test
试验过程中发现,有73%的棉籽沿垂直长度方向产生裂纹并破碎为两个质量相近的碎片,27%的棉籽沿长度方向产生裂纹。不同尺寸棉籽破碎力F、破碎能E′存在较强的离散性,与玉米情况类似[26],表明同一种农业物料之间的力学特性差异较大。
3.2 Tavares模型破碎参数拟合标定
通过棉籽压力-位移曲线,能够计算颗粒破碎比能。颗粒破碎比能等于初始接触点和破碎点之间的压力-位移曲线下的面积除以相应颗粒质量。其计算公式为
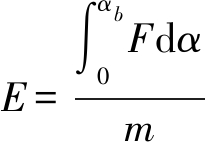
(12)
式中 F——棉籽加载过程中破碎力,N
α——棉籽加载过程中压头位移,mm
αb——棉籽达到破碎点时压头位移,mm
m——棉籽颗粒质量,g
将数据导入Origin软件,计算得到各组有效试验中棉籽颗粒破碎比能E,对其进行统计得到棉籽颗粒破碎比能排列顺序。将上述数据代入式(4)计算棉籽破碎概率,通过式(5)和式(6)拟合标定,使用Origin软件绘制出破碎概率-破碎比能曲线(图9)。
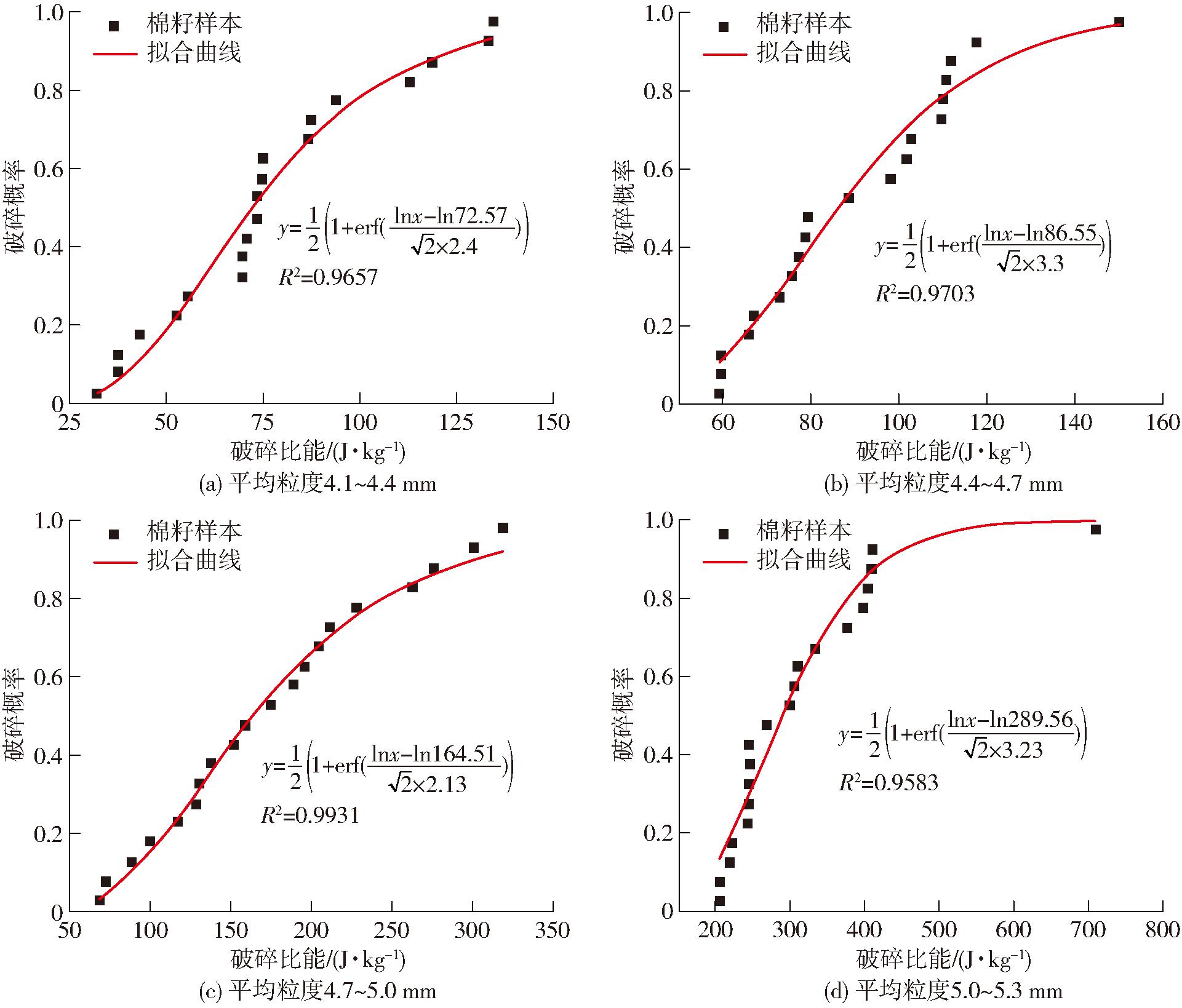
图9 棉籽破碎概率-破碎比能拟合曲线
Fig.9 Cottonseed crushing probability-crushing specific energy fitting curves
曲线拟合得到4组棉籽颗粒破碎比能中值E50和棉籽颗粒破碎概率对数正态分布标准差σ依次为72.57、86.55、164.51、289.56 J/kg与2.40、3.30、2.13、3.23。样本标准差σ较大,表明样本数据离散程度较大,这是由于棉籽外形不规则以及力学性能差异导致的。随着平均粒度减小,棉籽破碎比能E呈下降趋势,与矿石趋势相反[27]。分析棉籽与矿石的结构差异,可能是由于棉籽壳与棉籽仁之间的空隙随棉籽平均粒度增加而增大。在到达破碎点时,平均粒度越大的棉籽所需的压缩位移越长,由式(12)可得,其破碎比能E也会随之增加。
在标定时通过重复测定不同粒径范围的颗粒破碎比能中值E50,对式(7)中的参数进行拟合,但由于棉籽平均粒度变化范围较小,无法直接进行拟合。根据棉籽平均粒度的实际分布情况,取各组样本破碎比能中值E50加权平均值159.39 J/kg;参照Rocky DEM用户手册,将d0和φ设为默认值,对式(7)进行求解,得到棉籽颗粒剩余破碎比能E∞为61.28 J/kg。
由于在压缩试验中对棉籽只进行了单次加载,不存在循环加载过程,因此将相关参数设定为默认值。参照文献[28],在Rocky DEM中进行压缩仿真,对参数进行拟合。试验时将颗粒生成于承压平板上,圆柱压头以速度1 cm/min对颗粒加载,直到颗粒破碎生成子颗粒,调整参数范围,完成其余参数的设定。
3.3 仿真压缩试验验证
在完成棉籽破碎参数标定后,进行5次仿真压缩试验,通过统计破碎力F和破碎能E′的平均值,与实际试验结果比较,完成对Tavares模型验证,参数设置如表5所示。
表5 Tavares模型破碎参数设置
Tab.5 Tavares model crushing parameter setting
参数数值σ2.72E∞/(J·kg-1)61.28d0/mm400φ0.45γ5A0.633b′0.02dmin/mm2.3d∗min33.97
仿真时将颗粒生成于承压平板上,圆柱压头以速度1 cm/min对颗粒加载,待颗粒破碎后从后处理界面导出压缩力随时间变化曲线,导入Origin软件绘制压力-位移曲线。
图10a展示了试验压力-位移曲线,其主要分为3部分:塑性变形区、弹性变形区和破碎区。在塑性变形区,由于棉籽表面不规则,在加载的作用下首先产生塑性变形,此时压力随位移缓慢增加,压力-位移曲线斜率较小且斜率不断增大;在弹性变形区,在加载作用下棉籽产生弹性变形,此时压力随位移迅速增加,压力-位移曲线的斜率近似恒定;在破碎区,棉籽达到压缩强度极限,此时曲线斜率急剧下降,随后迅速上升。
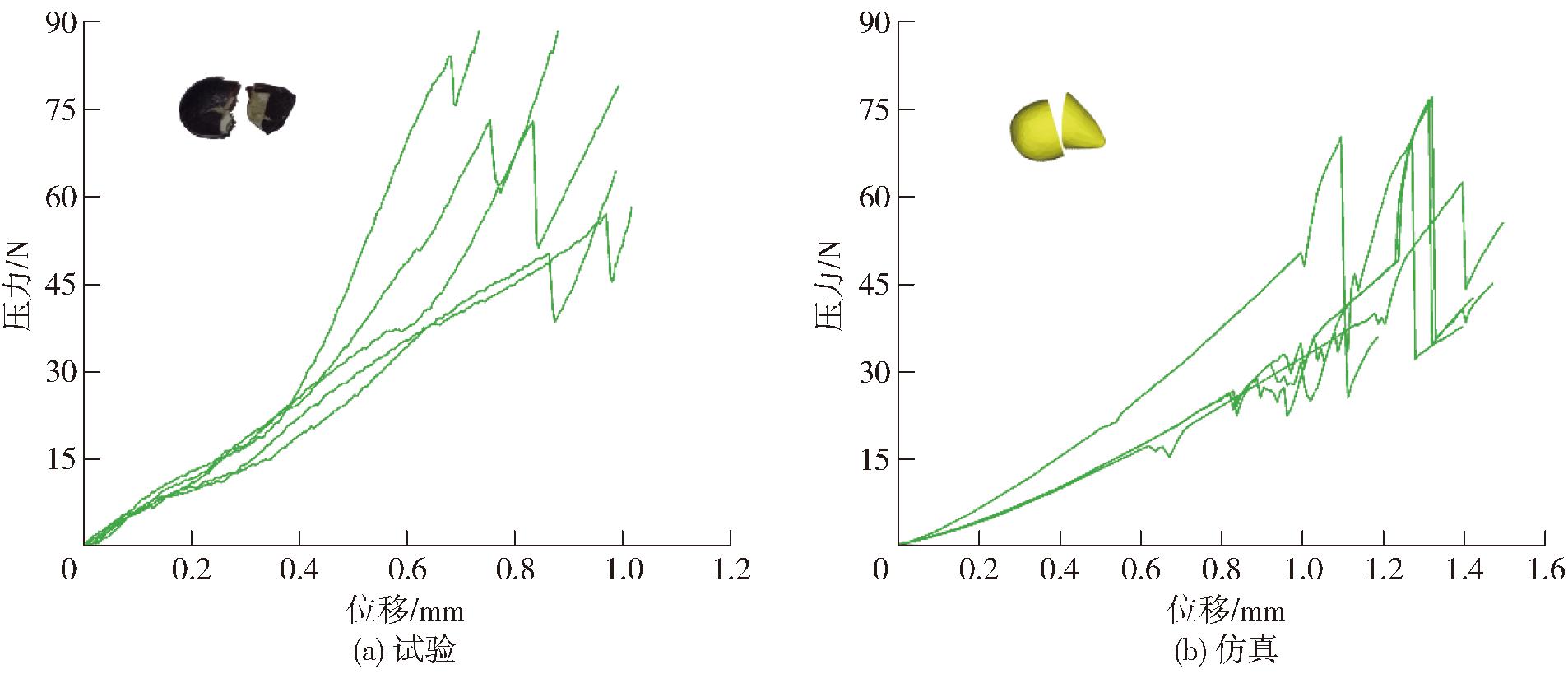
图10 棉籽试验压力-位移曲线与仿真压力-位移曲线对比
Fig.10 Comparisons of cottonseed test pressure-displacement curves and simulation pressure-displacement curves
图10b展示了仿真压力-位移曲线,与实际情况相似,仿真压力-位移曲线整体呈增长趋势。仿真曲线塑性变形阶段较长,且斜率在塑性变形阶段变化较小;在破碎点前,压力短暂下降随后迅速上升,可能是由于压缩时棉籽模型发生微小滚动引起。由于仿真中只考虑颗粒单次压缩破碎,破碎后尺寸较小的子颗粒被移出计算域,因此压力-位移曲线斜率未急速上升,与实际情况存在一定差异。
根据压力-位移曲线统计破碎力F和破碎能E′平均值如表6所示,两者相对误差均小于3%,表明Tavares模型参数准确,能够较好地描述棉籽破碎过程。
表6 破碎试验结果对比
Tab.6 Comparison of crushing test results
指标参数破碎力F/N破碎能E′/(N·mm)试验值73.0128.52仿真值71.2829.34相对误差/%2.372.87
4 结论
(1)基于三维扫描技术,通过Solidworks 2022的网格建模功能,提出了一种多面体离散元物料模型的快捷建模方式,并分析体积相对误差及仿真时间与模型分面数量的关系,最终选择多面体棉籽模型分面数量为1 098。
(2)通过堆积角试验,对棉籽间接触参数进行响应面分析,得到棉籽-棉籽碰撞恢复系数F1、棉籽-棉籽静摩擦因数F2对堆积角影响显著,棉籽-棉籽滚动摩擦因数F3对堆积角影响不显著,其最优参数组合为0.106、0.248、0.105。在最优参数组合下仿真堆积角与实际堆积角相对误差为0.28%。
(3)根据单颗粒压缩试验结果,通过方程拟合标定Tavares模型参数,并与仿真压缩试验结果进行对比,棉籽破碎力F与破碎能E′相对误差分别为2.37%和2.87%,验证了棉籽模型及Tavares模型参数标定的准确性。
[1] 刘君,王如南,邵会,等.棉籽粕生产棉籽蛋白及棉子糖工艺优化[J].中国油脂, 2024, 49(2): 101-103, 136.LIU Jun, WANG Ru’nan, SHAO Hui, et al. Process optimization of cottonseed protein and raffinose production from cottonseed meal[J]. China Oils and Fats, 2024, 49(2): 101-103,136. (in Chinese)
[2] 刘永明,关淑仙,王文静,等.棉籽作畜禽饲料的营养价值、脱毒方法及应用研究进展[J].中国棉花,2023,50(9):35-41.LIU Yongming, GUAN Shuxian, WANG Wenjing, et al. Nutritional value, detoxification methods, and application research of cottonseed as animal feed[J]. China Cotton, 2023,50(9):35-41. (in Chinese)
[3] 张军,王沙沙,韩建峰,等.齿辊剥壳机不同拉丝辊角度对光棉籽破碎的研究[J/OL].中国油脂:1-5.https:∥doi.org/10.19902/j.cnki.zgyz.1003-7969.220804.
[4] 柏云爱,张春辉.我国油料预处理技术的现状及发展趋势[J].中国油脂,2005,(7):12-17.
[5] 赵金标,孙志强,刘岭.棉籽蛋白营养价值及其在仔猪饲粮中的应用前景[J].动物营养学报,2023,35(10):6121-6128. ZHAO Jinbiao, SUN Zhiqiang, LIU Ling. Nutritive value of cottonseed protein and its application prospect in piglets’ diet[J]. Chinese Journal of Animal Nutrition, 2023,35(10):6121-6128. (in Chinese)
[6] RODNIANSKI V, LEVY A, KALMAN H, et al. A new method for simulation of comminution process in jet mills[J]. Powder Technology, 2019, 343:867-879.
[7] SU Yuan, XU Yang, CUI Tao, et al. Determination and interpretation of bonded-particle model parameters for simulation of maize kernels[J]. Biosystems Engineering, 2021, 210:193-205.
[8] 刘磊,杜岳峰,栗晓宇,等. 基于离散元法的种子玉米剥皮过程籽粒损失分析与试验[J]. 农业机械学报, 2022, 53(增刊2): 28-38.LIU Lei, DU Yuefeng, LI Xiaoyu, et al. Analysis and experiment on kernel loss of seed corn during peeling based on DEM[J]. Transactions of the Chinese Society for Agricultural Machinery, 2022, 53(Supp.2): 28-38. (in Chinese)
[9] 牛智有,江善晨,孔宪锐,等. 膨化颗粒饲料碰撞破碎特性分析与离散元模拟仿真[J]. 农业机械学报, 2023, 54(8): 371-380.NIU Zhiyou, JIANG Shanchen, KONG Xianrui, et al. Impact breakage characteristics and discrete element simulation of extruded pellet feed[J]. Transactions of the Chinese Society for Agricultural Machinery, 2023, 54(8): 371-380. (in Chinese)
[10] 张喜瑞,胡旭航,刘俊孝,等. 香蕉秸秆离散元仿真粘结模型参数标定与试验[J]. 农业机械学报, 2023, 54(5): 121-130.ZHANG Xirui, HU Xuhang, LIU Junxiao, et al. Calibration and verification of bonding parameters of banana straw simulation model based on discrete element method[J]. Transactions of the Chinese Society for Agricultural Machinery, 2023, 54(5): 121-130. (in Chinese)
[11] 张佳喜,张彭,张虎,等. 新疆棉花秸秆离散元仿真参数标定研究[J]. 农业机械学报, 2024, 55(1): 76-84, 108.ZHANG Jiaxi, ZHANG Peng, ZHANG Hu, et al. Discrete element simulation parameters calibration for Xinjiang cotton straw[J]. Transactions of the Chinese Society for Agricultural Machinery, 2024, 55(1): 76-84, 108. (in Chinese)
[12] 都鑫,刘彩玲,姜萌,等.基于离散元的包膜肥料Bonding模型参数标定[J].农业机械学报,2022,53(7):141-149.DU Xin, LIU Cailing, JIANG Meng, et al. Calibration of Bonding model parameters for coated fertilizers based on discrete element method[J].Transactions of the Chinese Society for Agricultural Machinery, 2022,53(7):141-149. (in Chinese)
[13] WEERASEKARA N S, POWELL M S, CLEARY P W, et al. The contribution of DEM to the science of comminution[J]. Powder Technology, 2013, 248:3-24.
[14] TAVARES L M, CHAGAS A S. A stochastic particle replacement strategy for simulating breakage in DEM[J]. Powder Technology, 2021, 377:222-232.
[15] BARRIOS G K, JIMÉNEZ-HERRERA N, FUENTES-TORRES S N, et al. DEM simulation of laboratory-scale jaw crushing of a gold-bearing ore using a particle replacement model[J]. Minerals, 2020, 10(8):1-16.
[16] 田辛亮,丛旭,齐江涛,等.黑土区玉米秸秆-土壤混料离散元模型参数标定[J].农业机械学报, 2021, 52(10): 100-108, 242.TIAN Xinliang, CONG Xu, QI Jiangtao, et al. Parameter calibration of discrete element model for corn straw-soil mixture in black soil areas[J]. Transactions of the Chinese Society for Agricultural Machinery, 2021, 52(10): 100-108, 242. (in Chinese)
[17] 陈永,高晓勋,金鑫,等.油莎豆排种离散元仿真参数标定与试验[J].农业机械学报,2023,54(12):58-69.CHEN Yong, GAO Xiaoxun, JIN Xin, et al. Calibration and analysis of seeding parameters of Cyperus esculentus seeds based on discrete element simulation[J]. Transactions of the Chinese Society for Agricultural Machinery, 2023,54(12):58-69. (in Chinese)
[18] 胡梦杰,周勇,汤智超,等.脱绒包衣棉花种子的力学特性[J].安徽农业大学学报, 2018, 45(1): 175-180.HU Mengjie, ZHOU Yong, TANG Zhichao, et al. Mechanical properties of the delinted and coated cottonseed[J]. Journal of Anhui Agricultural University, 2018, 45(1): 175-180. (in Chinese)
[19] TAVARES L M. Review and further validation of a practical single-particle breakage model:review papers[J]. KONA Powder and Particle Journal, 2022, 39:62-83.
[20] TAVARES L M, KING R P. Single-particle fracture under impact loading[J]. International Journal of Mineral Processing, 1998, 54(1):1-28.
[21] TAVARES L M, ANDRÉ F P, POTAPOV A, et al. Adapting a breakage model to discrete elements using polyhedral particles[J]. Powder Technology, 2020, 362:208-220.
[22] 郝建军,魏文波,黄鹏程,等.油葵籽粒离散元参数标定与试验验证[J].农业工程学报,2021,37(12):36-44.HAO Jianjun, WEI Wenbo, HUANG Pengcheng, et al. Calibration and experimental verification of discrete element parameters of oil sunflower seeds[J]. Transactions of the CSAE,2021,37(12):36-44. (in Chinese)
[23] 王龙,贺小伟,胡灿,等.包衣棉种物性参数测定与离散元仿真参数标定[J].中国农业大学学报, 2022, 27(6): 71-82.WANG Long, HE Xiaowei, HU Can, et al. Measurement of the physical parameters and calibration of discrete element simulation parameter of coated cottonseed[J]. Journal of China Agricultural University, 2022, 27(6): 71-82. (in Chinese)
[24] YAN Dongxu, YU Jianqun, LIANG Liusuo, et al. A comparative study on the modelling of soybean particles based on the discrete element method[J]. Processes, 2021, 9(2):286.
[25] JYOTIRMAY M, SHANKER T P, PRATAP S K, et al. Analysis of cotton (Gossypium hirsutum) seed properties for engineering applications[J]. Current Advances in Agricultural Sciences(An International Journal), 2022, 14(1):27-33.
[26] CHEN Zhengpu, CARL W, KINGSLY A, et al. Development and validation of a DEM model for predicting compression damage of maize kernels[J]. Biosystems Engineering, 2023, 230:480-496.
[27] 谢浩松.北衙金矿半自磨钢球运动能量与矿石断裂能的匹配机制[D].昆明:昆明理工大学,2023.
[28] GABRIEL C A, MAR
A C I, JULIANA P, et al. DEM breakage calibration for single particle fracture of maize kernels under a particle replacement approach[J]. Chemical Engineering Research and Design, 2023, 195:151-165.
