0 引言
随着智能农业装备的推广,智能导航技术在农机领域受到了广泛关注,局部路径规划是智能导航控制的核心技术之一。针对不同的农业机械和作业场景优化局部路径规划,提高作业机具跟踪精度,有助于提高作业质量,对农业无人化生产有重要意义[1-4]。
履带底盘因具有通过性好、土壤压实小的优点,在农业机械中得到大量应用[5-9]。单侧制动式履带底盘通过切断单侧履带动力的方式实现转向[10-11],主要分为比例控制和点动控制两种,其中比例控制转弯半径与控制力度相关,常用于人工驾驶,而点动控制因其结构简单、便于操作的优点常用于遥控电动作业农机[12-16],但是点动控制转弯半径与行驶速度、液压压力等因素相关[17-18],很难实现精准控制,因此有必要针对其特性进行局部路径规划研究。
基于几何原理的局部路径规划算法在农机领域应用较多[19],其中最经典的是纯追踪模型。纯追踪模型通过车辆当前横向偏差、航向偏差和前视距离来规划弧形行驶轨迹,根据几何关系计算当前状态转弯半径,从而得出两侧履带目标转速[20-21],这种方法需要明确控制参数与转弯半径之间的关系,适用于两侧履带速度可测可控的底盘,不能直接应用于通过液压阀控制转向的单侧制动式履带底盘。近年来,众多学者针对单侧制动式履带底盘局部路径规划展开了研究,吴明阳等[22]针对纯追踪算法导致电磁阀频繁切换问题,引入bang-bang控制算法,通过借鉴滑膜控制原理增加边界层修改控制规律,降低电磁阀切换频率以保护控制系统,但随着边界层厚度的增加,跟踪精度也随之下降;何永强等[23]基于履带收获机转向特性提出了预瞄-切线法动态规划方法,该方法由两段相切圆弧组成,第1段圆弧在1/2横向偏差线上通过前视距离设置预瞄点,根据纯追踪模型得出转弯半径,第2段圆弧根据到达预瞄点后的位姿和期望路径的切线确定,通过构建转向控制模型获得转向控制参数与转弯半径之间的关系,实现局部路径规划,此算法通过构建转向控制模型得出速度、转向控制参数与转弯半径的关系,能够通过改变控制参数修正两段圆弧的转弯半径,不适用于单侧点动制动式履带底盘,在计算转弯半径时相比纯追踪算法需要额外获得车辆纵向坐标,适用范围受限,且其未考虑在2个圆弧转向切换时系统响应延时带来的影响。
综上所述,基于单侧制动式履带底盘局部路径规划算法基本上通过2个步骤实现:第1步农机趋向目标航线转向,以减小横向偏差,第2步农机向远离目标航线转向,以减小航向偏差、避免过调。在实际应用过程受液压转向响应延迟的影响,两次相反的转向会有一定的时间间隔,在此时间内农机沿直线行驶,会对路径规划和转向效果产生一定影响;并且在第1次转向结束时,农机处于较大的航向偏差,农机作业过程中航向偏差变化会对作业机具的作业效果产生较大的影响。
针对单侧点动制动式履带底盘局部路径规划的上述问题,本文提出一种基于单侧制动转向履带底盘的三切线局部路径动态规划算法,根据履带底盘转向制动力矩不可控特性,设计 “转向-直行-转向”的局部路径规划方式,根据车辆当前状态实时调整控制策略,通过搭建温室用履带式电动作业平台进行田间试验,对本文方法进行验证。
1 材料与方法
1.1 履带底盘平台
为了验证三切线局部路径规划的实际效果,针对点动式单侧制动转向履带底盘搭建了EWT10型温室用智能电动动力平台,如图1所示。作业平台采用磷酸铁锂电池供电,行走电机通过前桥驱动履带底盘行驶,前桥轮毂通过微型液压缸推动制动器动作,实现履带底盘转向与制动,作业平台装配液压系统,为悬挂系统和制动油缸提供动力,作业平台主要技术参数如表1所示。
表1 EWT10型温室用智能电动动力平台参数
Tab.1 Parameter of EWT10 intelligent electric power platform for greenhouse
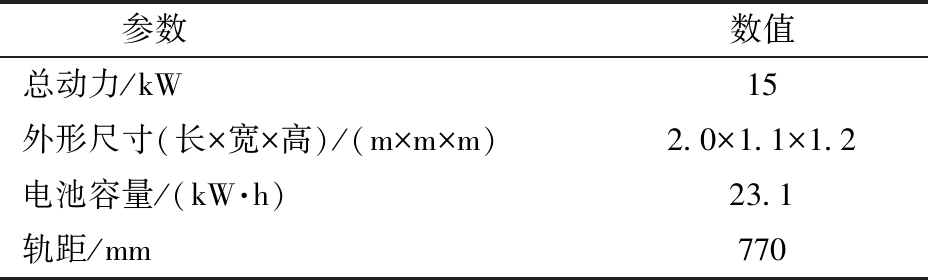
参数数值总动力/kW15外形尺寸(长×宽×高)/(m×m×m)2.0×1.1×1.2电池容量/(kW·h)23.1轨距/mm770

图1 EWT10型温室用智能电动动力平台
Fig.1 EWT10 intelligent electric power platform for greenhouse
作业平台导航系统搭载1台Velodyne-16多线激光雷达,其垂直视场角为±15°,水平扫描视场角为360°,水平方向角度分辨率为0.2°,测量量程为100 m,扫描测量频率为10 Hz。配套研华工控机,可高效获取环境信息,为系统提供作业平台实时横向偏差de和航向偏差θ,导航系统测量的横向偏差精度为±15 mm,航向偏差精度为±0.3°。控制系统以西门子S7-200PLC作为底层控制器,与工控机通过RS485协议通讯,能够接收遥控器信号和工控机指令,对作业平台电机与电磁阀进行控制,以实现作业平台行驶与转向。
1.2 三切线局部路径规划算法
局部路径规划为农机导航提供当前位置到目标航线之间的转向控制决策,符合农机底盘转向特性的局部路径规划方案可以提高农机导航精度。三切线局部路径规划算法主要针对单边制动转向的履带底盘,该底盘通过液压油缸动作使单侧驱动轮制动以实现转向功能,具有结构简单、控制方便等优点,但其转弯半径受行驶速度、液压压力等影响,具有不可控性。本文中假设在短时间内两次转弯期间转弯半径不产生突变。
三切线局部路径规划算法由2条半径相等的圆弧和1条切线组成,如图2所示,圆弧BC和圆弧DE半径相等,均为R,直线CD与2个圆弧相切,直线AE为目标航线,直线AB长度为作业平台当前位置与目标航线的横向偏差,θ为当前航向偏差,Oc为作业平台当前坐标位置,O1和O2分别为2次转向圆弧的圆心,Ld为前视距离。
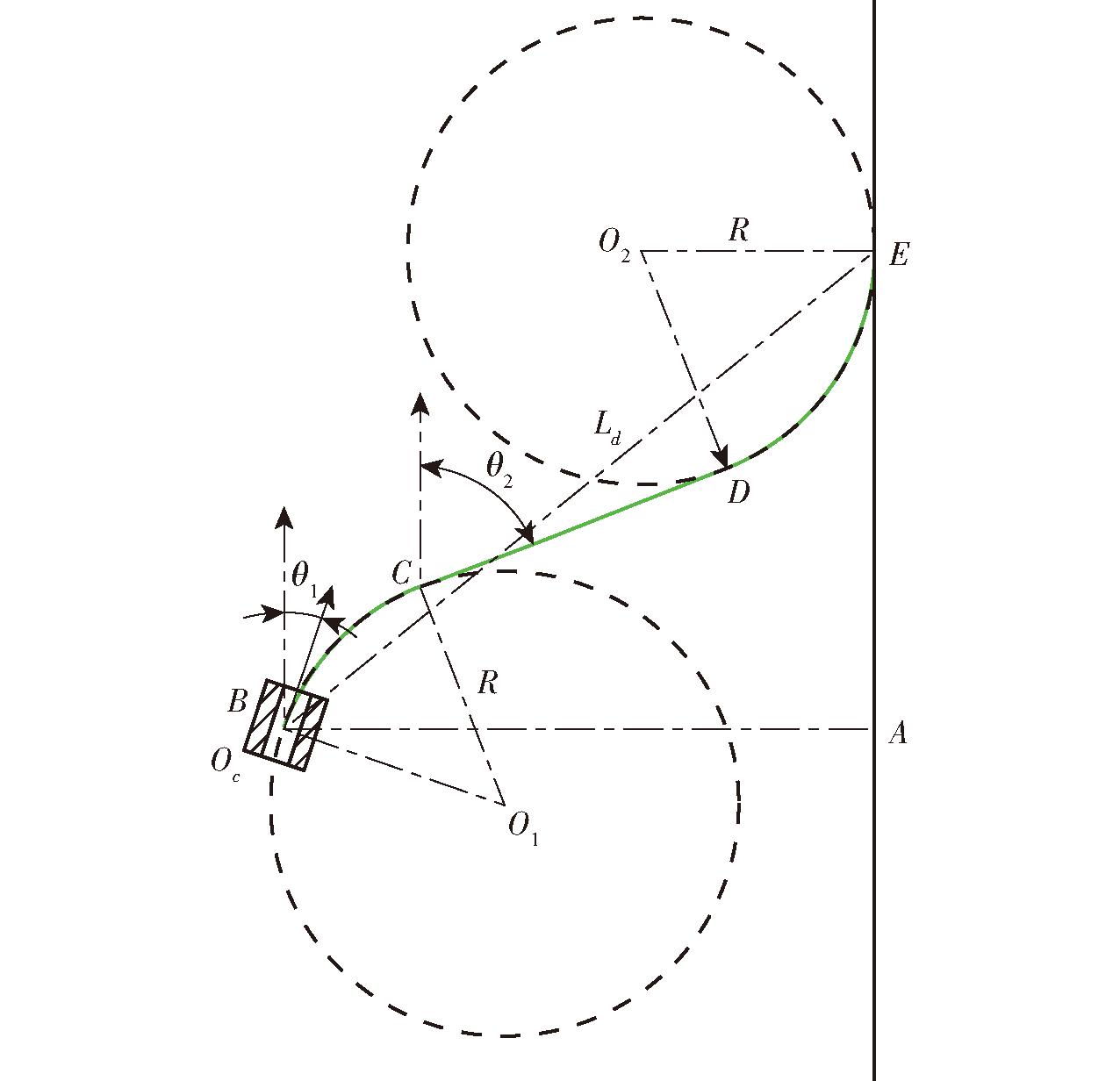
图2 三切线局部路径规划示意图
Fig.2 Three-tangent local path planning
在第1阶段,作业平台沿圆弧BC进行转向,调整作业平台航向偏差,并且根据横向偏差和航向偏差计算转弯半径R;第2阶段,作业平台沿直线CD行驶,调整横向偏差,直至作业平台的横向偏差和航向偏差满足下一阶段转向要求;第3阶段作业平台沿圆弧DE进行转向,调整航向偏差,直至作业平台横向偏差和航向偏差达到阈值即完成局部路径调节。三切线局部路径规划算法通过2次转向和1段直线行驶完成对作业平台的调节,在调节过程中根据作业平台的横向偏差和航向偏差实时判断所处阶段并动态调整转向时机,逐步逼近目标航线,最终达到横向偏差和航向偏差均处于设定阈值内状态,直线段的引入能够降低控制频率,减小第1阶段转向时的航向偏差,提高局部路径规划稳定性。
1.3 转向半径确定方法
在一定时间内,作业平台液压系统的压力和行驶速度相对稳定,可视为在2次转向期间转弯半径不变。当前的转弯半径可根据作业平台一定时间内的横向偏差和航向偏差进行计算,当前转向阶段的转弯半径可为下一阶段转向决策提供参考。
在转弯状态下,如图3所示,Oc(t)、θ(t)、R(t)和de(t)分别为t时刻作业平台的坐标位置、航向偏差、转弯半径和横向偏差,根据作业平台移动的几何关系,可通过t时刻和t-1时刻的横向偏差和航向偏差计算出当前位置转弯半径,计算式为
(1)
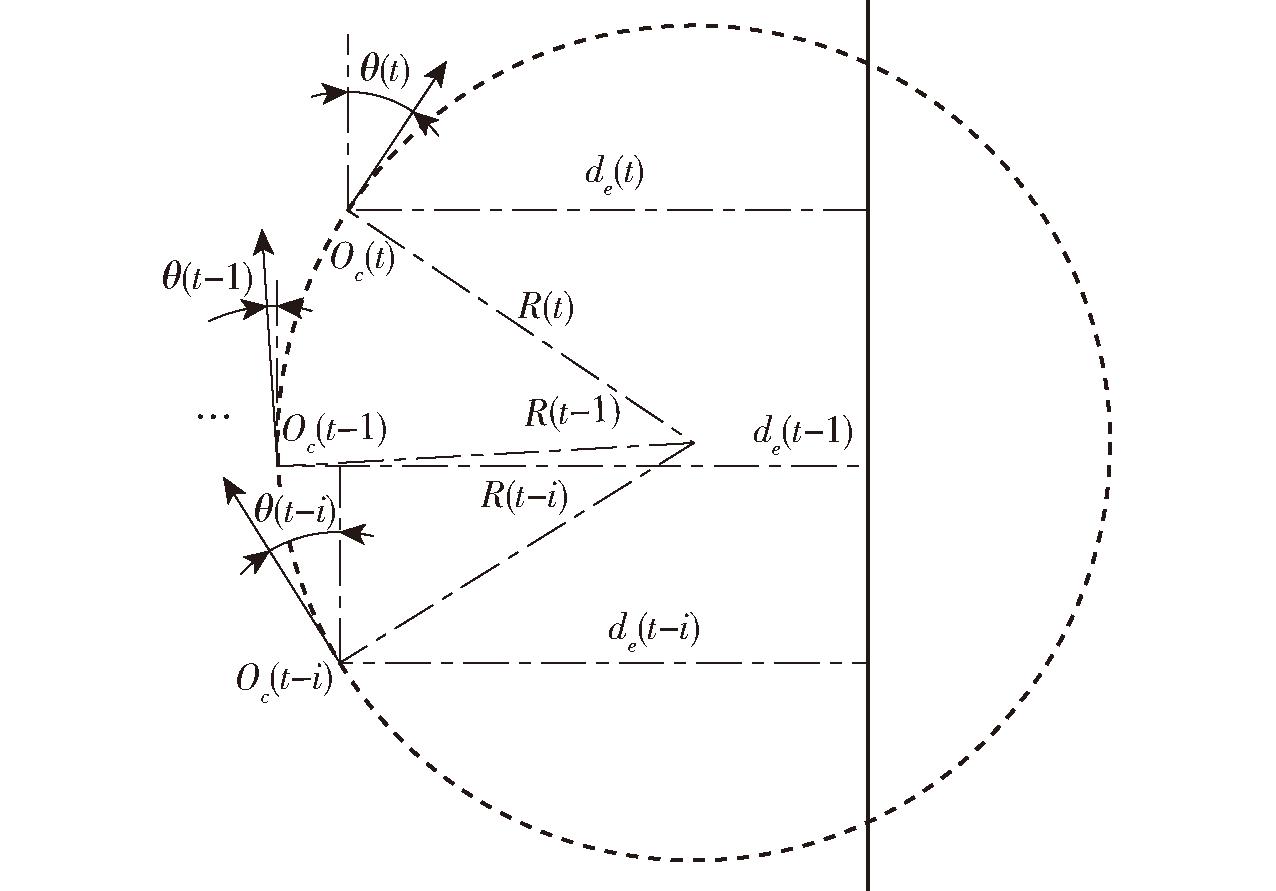
图3 转弯半径求解示意图
Fig.3 Turning radius solution
在转弯过程中,考虑到横向偏差和航向偏差测量误差对转弯半径计算精度有较大的影响,为了提高转弯半径计算稳定性,减少测量误差带来的波动,采用加权递推平均滤波算法[24]对转弯半径进行计算,加权递推平均滤波算法适用于作业平台转弯过程中转弯半径变化不大的场景。转弯半径计算式为
(2)
式中 n——加权半径数量
1.4 基于模糊推理的前视距离求解方法
前视距离是局部路径规划中的一个关键参数,合理地设置前视距离能提高作业平台跟踪效果[25],前视距离偏大,作业平台能很好地调整到位,但会导致作业平台调整缓慢,前视距离偏小,作业平台会有较大的转动幅度,出现超调现象,从而导致作业平台在行驶过程中走“S弯”。模糊控制采用模糊逻辑和近似推理的方法,对专家经验知识进行模型化,适用于前视距离求解这样的非线性控制场景[26]。
在作业平台行驶过程中,影响其跟踪精度的主要因素有行驶速度v、横向偏差de和航向偏差θ,通常情况下行驶速度不会有较大的变化,横向偏差de和航向偏差θ是对跟踪进度影响最为敏感的参数,且局部路径规划的目的是使横向偏差de和航向偏差θ均趋近于零。本文以横向偏差de和航向偏差θ为模糊控制器输入,前视距离为输出,横向偏差de基本论域为[-0.3 m,0.3 m],偏左为正,偏右为负,量化等级为{-1,-0.5,0,0.5,1}={NB,NS,ZO,PS,PB},量化因子为10/3;航向偏差θ基本论域为[-30°,30°],偏左为正,偏右为负,量化等级为{-1,-0.5,0,0.5,1}={NB,NS,ZO,PS,PB},量化因子为1/30;前视距离基本论域为[1 m,3 m], 量化等级为{0.2,0.4,0.6,0.8,1}={S,M,Z,L,BL},量化因子为2/5。3个参数均采用三角隶属度函数对其模糊化,采用加权平均法对其反模糊化。模糊控制规则如表2所示,模糊控制曲面如图4所示。
表2 模糊控制规则
Tab.2 Fuzzy control rule
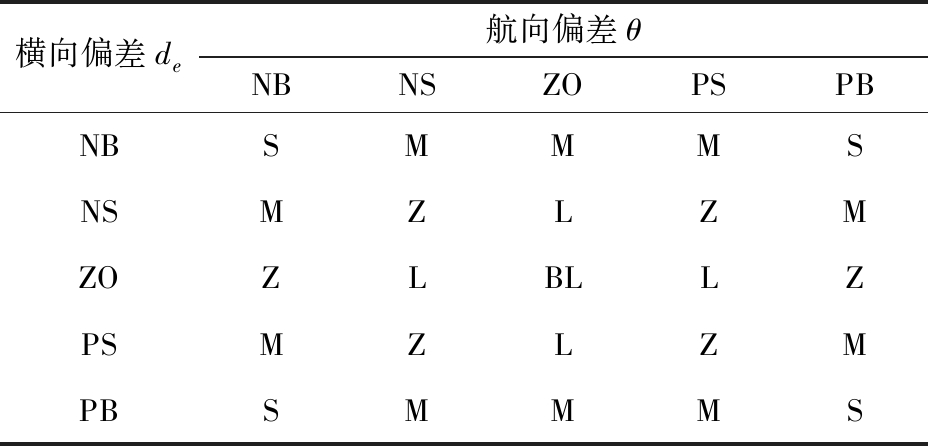
横向偏差de航向偏差θNBNSZOPSPBNBSMMMSNSMZLZMZOZLBLLZPSMZLZMPBSMMMS
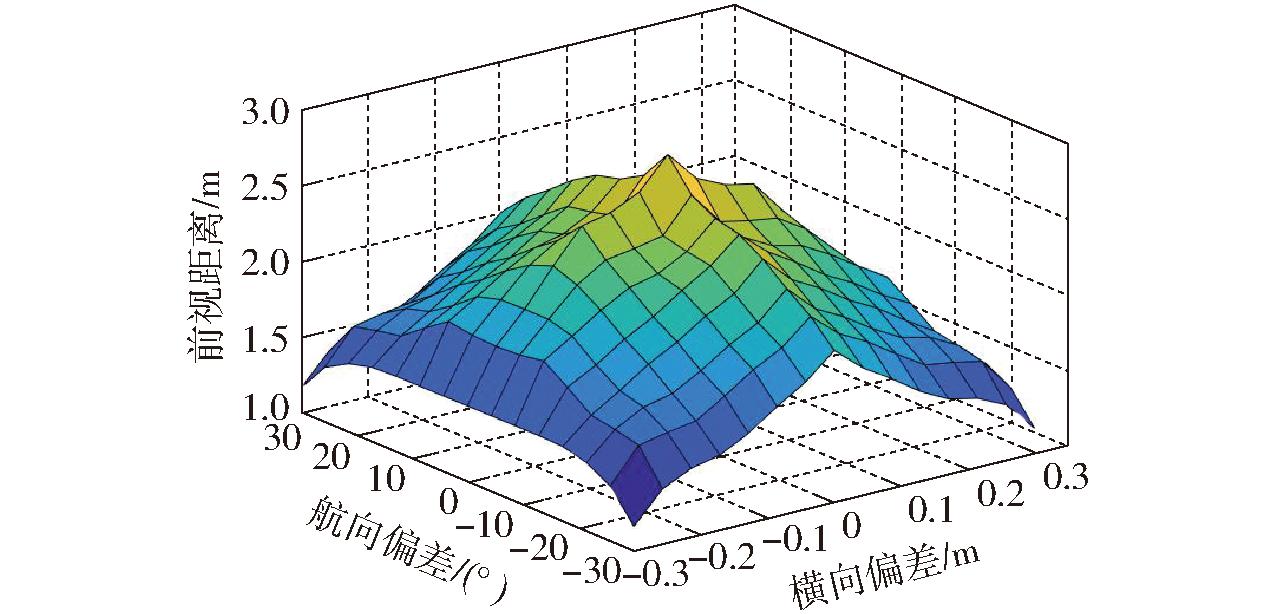
图4 模糊控制曲面
Fig.4 Surface of fuzzy model
1.5 局部路径规划算法
在局部路径规划过程中,针对作业平台当前横向偏差和航向偏差进行实时规划和调整,当前状态的评估和转向节点的规划对局部路径规划过程尤为重要。
三切线局部路径规划过程中作业平台会处于3个阶段中的任意一段,需要根据当前状态进行实时判断。如图5所示,首先判断作业平台是否处于第3阶段,第3阶段作为最后姿态调整阶段,调节距离较短,不需要考虑前视距离,当deθ<0时,作业平台转向后是否达到目标航线附近的判断公式为
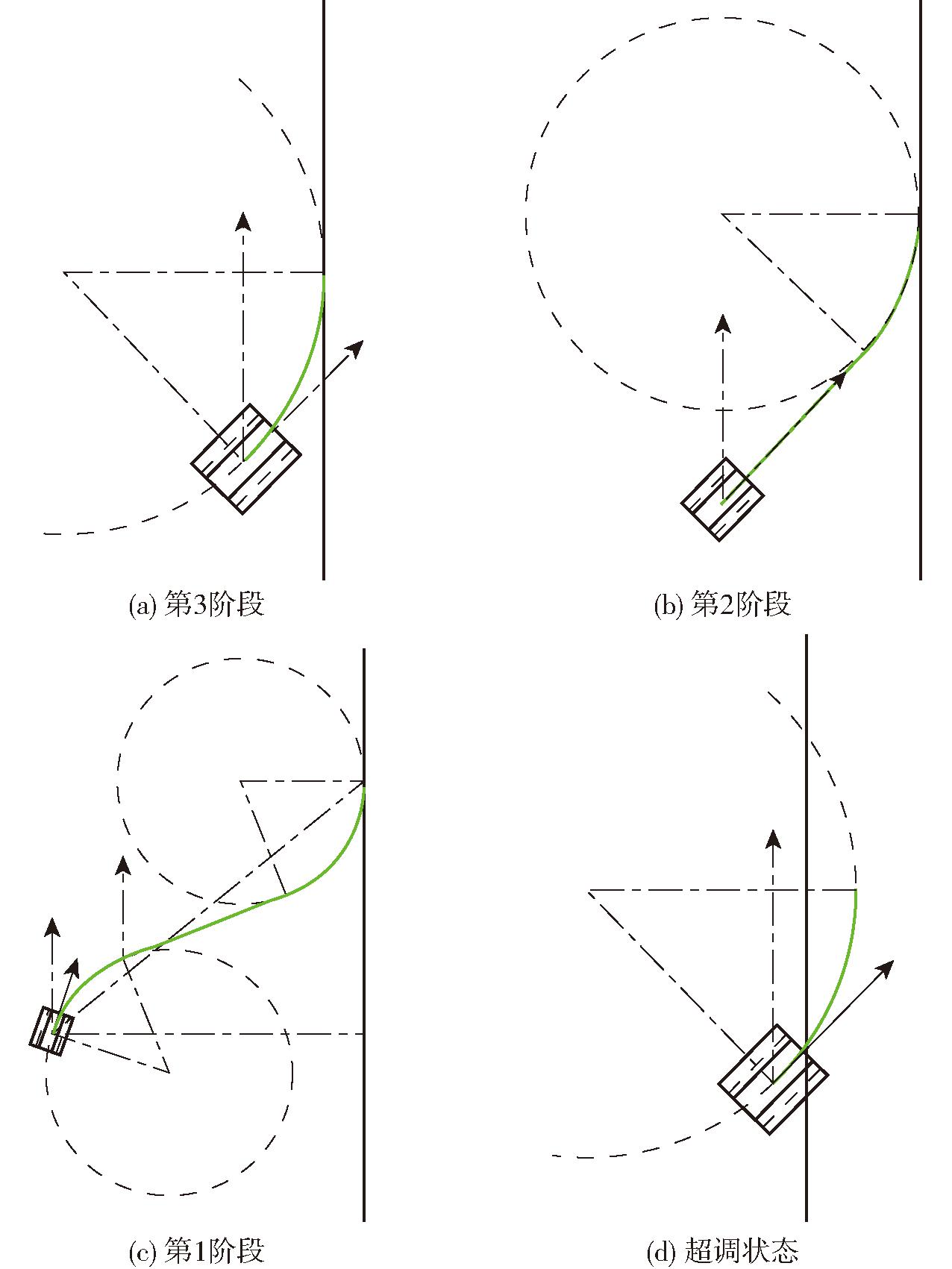
图5 不同阶段转向示意图
Fig.5 Diagrams of different stages of turning
de≤R-Rcosθ
(3)
当满足式(3)时为第3阶段,不满足时进入第2阶段的判断;第2阶段包含直线CD段直行过程,理论上直线CD段一定可以和圆弧DE段相切,但是航向偏差越小前视距离越大,所以将前视距离作为判断依据,判断公式为
(4)
当满足式(4)时,即按照第2阶段状态行驶的前视距离小于设定前视距离时,作业平台处于第2阶段;当不满足式(4)或者deθ>0时,作业平台处于第1阶段。
如图5所示,在第1阶段时,当de<0时向右转,否则向左转;在第2阶段作业平台保持直行;在第3阶段,当de<0时向左转,否则向右转。在一定条件下,作业平台按照第3阶段行驶至de=0后会出现反向超调,作业平台越过目标航线后会判断当前状态为第1状态,根据转向规则,转弯方向不会变化。
局部路径规划流程如图6所示,在路径规划过程中,只需要根据当前状态进行简单计算与判断,就能获得车辆所处控制阶段,根据每个控制阶段的转向规则进行转向即可,在计算和实现上相对更容易。
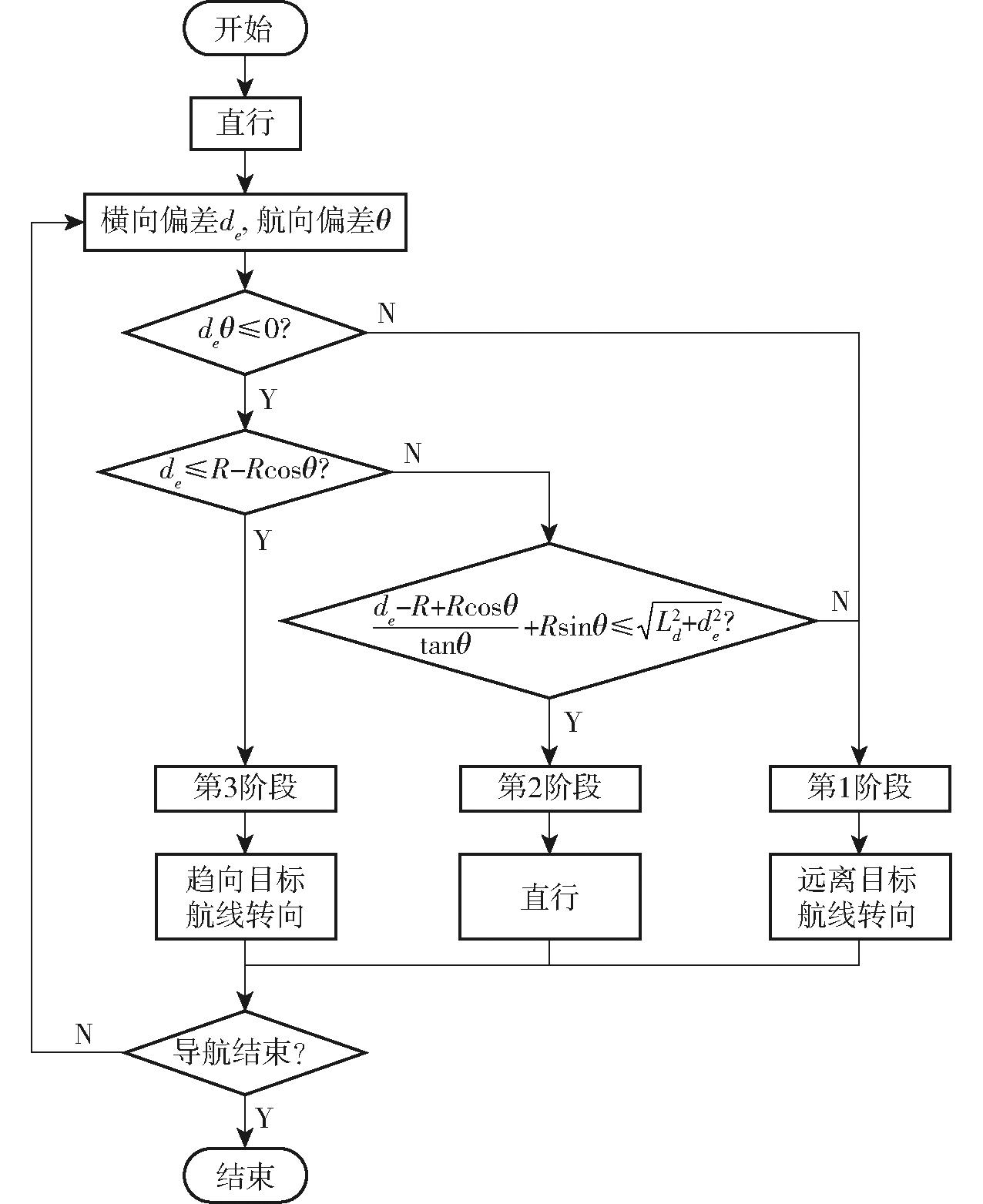
图6 局部路径规划流程图
Fig.6 Flowchart of local path planning
2 试验结果与分析
2.1 转弯半径测算试验
转弯半径的测算精度直接影响局部路径规划的状态评估和控制节点,针对单侧制动转向的作业平台转弯半径测算进行试验。由于在温室内测量转弯半径较为困难且测量精度低,故在露天环境采用高精度GNSS测量作业平台的转弯半径。如图7所示,在清除种植作物后的泥土路面,作业平台靠近墙面一侧行驶,以速度0.4 m/s进行转向,以墙面所在直线作为基准,激光雷达通过检测墙面反馈作业平台的横向坐标和航向偏差,计算理论转弯半径。作业平台上额外加装P3-DT型北斗高精度GNSS,用以获取作业平台的坐标位置,通过转向过程中坐标位置拟合圆形,获取作业平台实际转弯半径,试验结果如图8所示。

图7 转弯半径测算试验
Fig.7 Turning radius measurement test
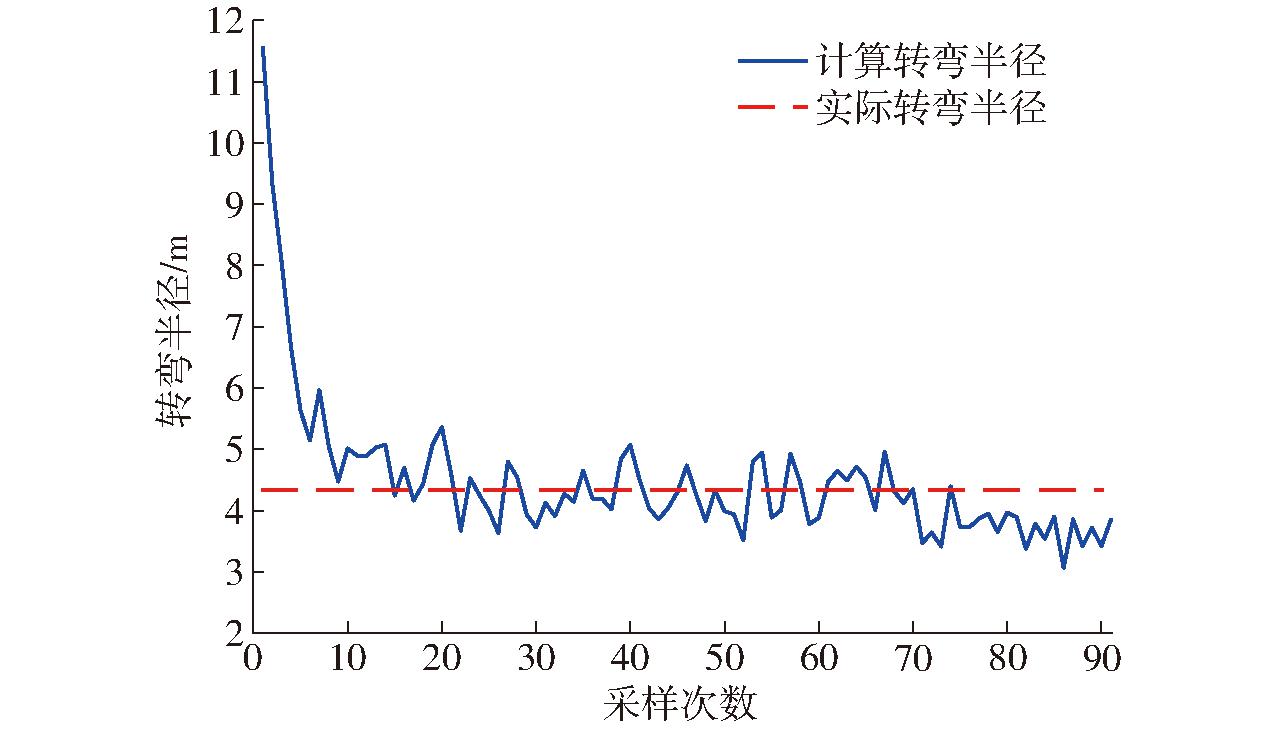
图8 转弯半径测算试验结果
Fig.8 Test results of turning radius measurement
通过GNSS数据拟合出的实际转弯半径为4.352 m,在转弯初期,计算得出的转弯半径较大,是由于此时加权递推平均滤波算法中部分数据仍是处于直线行驶状态的值,随着采样次数的增加会快速接近真实值。转弯后期的转弯半径较前期小,主要是随着制动时间的增加,车辆行驶速度会因制动力逐渐减小,转弯半径也随之变小。试验结果表明,本文计算方法能够有效地计算出转弯时车辆的转弯半径,且更贴近实际情况。
2.2 直线导航跟踪对比试验
为了进一步验证三切线局部路径规划方法的可靠性,分别采用bang-bang控制算法和三切线局部路径动态规划算法进行直线导航跟踪试验。bang-bang控制算法是基于纯追踪算法的思想所提出的路径跟踪控制算法,具有一定的代表性,其主要应用场景为开关阀控的单侧制动式履带,与本文应用场景一致。如图9所示,试验在温室大棚内进行,温室大棚为标准拱棚,大棚宽8 m,长约80 m,作业平台的横向坐标和航向偏差由激光雷达提供,设置初始位置横向偏差为0.25 m,航向偏差为0°,行驶速度为0.4 m/s。直线导航跟踪试验结果如图10所示。

图9 直线导航跟踪试验
Fig.9 Linear navigation tracking test
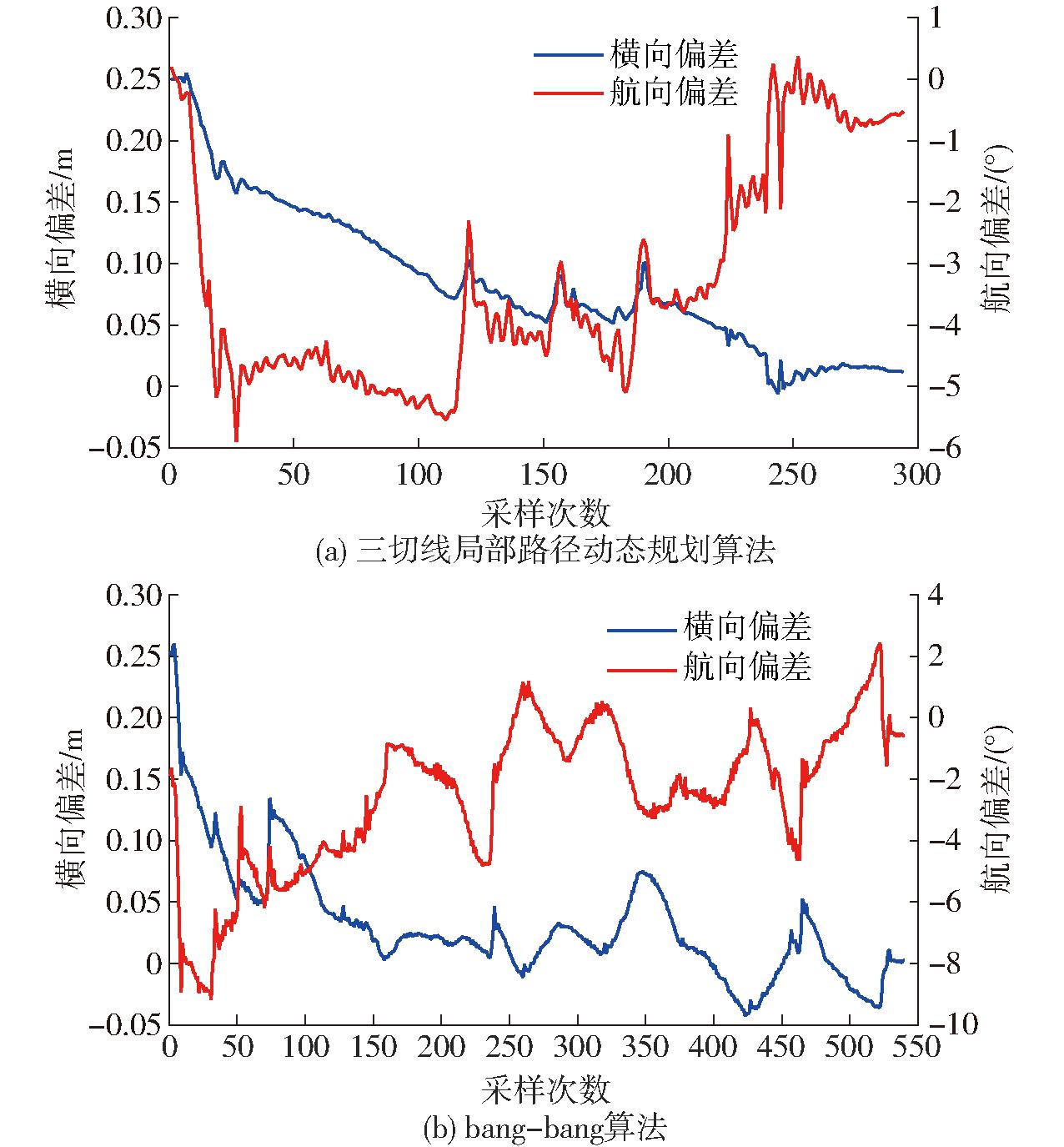
图10 直线导航跟踪试验对比
Fig.10 Comparison results of linear navigation tracking test
由图10可知,路径跟踪过程符合预期的3个阶段,在第1阶段,横向偏差较大,航向角快速增加以加快作业平台趋向目标航线行驶,两种算法航向角的变化幅度均比较大,三切线局部路径动态规划算法在达到一定航向角后进入直行状态,行驶较为平稳,而bang-bang算法出现多次的航向角调整;在第2阶段,航向角减小且变化较小,横向偏差进一步减小,三切线局部路径动态规划算法在这一阶段调整次数较少,处于直行和反向转向两种状态相互切换的阶段,航向角相对保持在较高的角度,而bang-bang算法由于横向偏差的减小而高频次地调整航向角,航向角在逐步减小;在第3阶段,横向偏差基本达到预设值,主要对航向角进行调整,三切线局部路径动态规划算法处于反向转向阶段,对航向角的调整时机较早,不断地快速减小航向角,使得航向与目标直线基本平行,最终达到航向偏差和横向偏差均在预期值内,而bang-bang算法在这一阶段由于转向阈值的设置导致出现超调现象,在最后阶段需要多次调整才能达到预期值。在整个过程中,本文算法航向角最大偏差相对较小,控制算法中直行阶段的加入能够使得整个调节过程更平稳,有利于农机挂载机具作业,bang-bang算法上线距离相对较短,但上线后出现超调导致需要多次调整,本文算法能够快速进入稳定状态,在距离目标航线较近的位置转向较为温和。
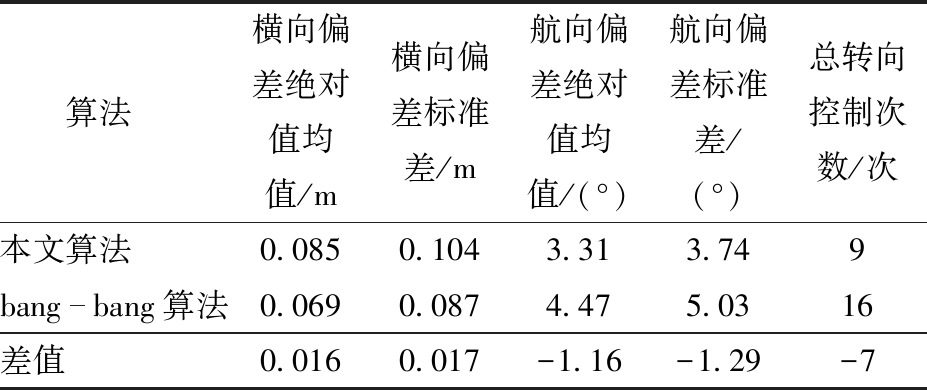
对两种算法在直线路径跟踪过程中的参数进行对比,结果如表3所示,主要包括横向偏差绝对值均值、横向偏差标准差、航向偏差绝对值均值、航向偏差标准差以及转向控制次数。其中偏差绝对值均值反映路径跟踪精度,偏差标准差和转向控制次数反映路径跟踪稳定性。为了更加清晰地进行对比,偏差绝对值均值和偏差标准差均采用从出发点到上线点间的数据进行计算。由表3可知,当前进速度为0.4 m/s时,本文算法的横向偏差绝对值均值和横向偏差标准差分别为0.085、0.104 m,分别比bang-bang算法增加23.19%、19.54%,航向偏差绝对值均值和航向偏差标准差分别为3.31°、3.74°,分别比bang-bang算法减少25.95%、25.64%,总转向控制次数为9次,比bang-bang算法减少43.75%。结合图10,在起点到上线阶段,航向偏差相对较小,能降低对作业机具的影响,由此导致横向偏差有所增加。试验结果表明,三切线局部路径动态规划算法在路径跟踪精度和稳定性上均优于传统算法,点动式单侧制动式转向履带底盘转向控制次数明显降低,减小电磁阀工作频率,能有效减少制动部件磨损,增加农机使用寿命。
表3 路径跟踪试验结果对比
Tab.3 Comparison of path tracking test results
算法横向偏差绝对值均值/m横向偏差标准差/m航向偏差绝对值均值/(°)航向偏差标准差/(°)总转向控制次数/次本文算法0.0850.1043.313.749bangbang算法0.0690.0874.475.0316差值0.0160.017-1.16-1.29-7
3 结论
(1)针对点动控制的单侧制动式转向履带底盘在自动行走中控制精度低、转向切换频繁的问题,提出了一种基于单侧制动转向履带底盘的三切线局部路径动态规划算法,根据履带底盘转向制动力矩不可控特性,设计了“转向-直行-转向”的局部路径规划方式。该算法简单明了,易于实现。
(2)通过分析履带底盘在转向过程中一定时间内转弯半径不变的特性,结合一定时间内的横向偏差和航向偏差,根据转向过程的几何关系,采用加权递推平均滤波算法减少测量误差带来的影响,解析当前转弯半径。
(3)基于本团队搭建的智能电动动力平台,进行转弯半径测算试验和直线导航跟踪对比试验,试验结果表明:三切线局部路径动态规划算法在路径跟踪精度和稳定性上均优于传统算法,在转向调节过程中有较小的航向偏差,能够有效地降低对作业机具的影响;针对点动式单侧制动式转向履带底盘转向控制次数明显降低,减小电磁阀工作频率,能有效减少制动部件磨损,增加农机使用寿命。可为农机自动导航路径跟踪控制提供参考。
[1] 刘成良, 林洪振, 李彦明, 等. 农业装备智能控制技术研究现状与发展趋势分析[J]. 农业机械学报, 2020, 51(1): 1-18.LIU Chengliang, LIN Hongzhen, LI Yanming, et al. Analysis on status and development trend of intelligent control technology for agricultural equipment[J]. Transactions of the Chinese Society for Agricultural Machinery, 2020, 51(1): 1-18.(in Chinese)
[2] 罗锡文, 廖娟, 臧英, 等. 我国农业生产的发展方向:从机械化到智慧化[J]. 中国工程科学, 2022, 24(1): 46-54.LUO Xiwen, LIAO Juan, ZANG Ying, et al. Developing from mechanized to smart agricultural production in China[J]. Strategic Study of CAE, 2022, 24(1): 46-54. (in Chinese)
[3] 张漫, 季宇寒, 李世超, 等. 农业机械导航技术研究进展[J]. 农业机械学报, 2020, 51(4): 1-18.ZHANG Man, JI Yuhan, LI Shichao, et al. Research progress of agricultural machinery navigation technology[J]. Transactions of the Chinese Society for Agricultural Machinery, 2020, 51(4) : 1-18. (in Chinese)
[4] ROSHANIANFARD A, NOGUCHI N, OKAMOTO H, et al. A review of autonomous agricultural vehicles (the experience of Hokkaido University)[J]. Journal of Terramechanics, 2020, 91: 155-183.
[5] 张拓, 岳高峰, 刘妤. 橡胶履带底盘的研究进展[J]. 重庆理工大学学报(自然科学版), 2018, 32(5): 82-88.ZHANG Tuo, YUE Gaofeng, LIU Yu. Research progress of rubber tracked chassis[J]. Journal of Chongqing University of Technology(Natural Science Edition), 2018, 32(5): 82-88. (in Chinese)
[6] WU L, WU Y. Simulation of transmission system of crawler self-propelled rotary tiller based on deep learning[J]. Computational Intelligence and Neuroscience, 2022, 2022: 6078223.
[7] LIU Z, ZHANG G, CHU G, et al. Design matching and dynamic performance test for an HST-based drive system of a hillside crawler tractor[J]. Agriculture, 2021, 11(5): 466.
[8] LIU J, XIA C, JIANG D, et al. Development and testing of the power transmission system of a crawler electric tractor for greenhouses[J]. Applied Engineering in Agriculture, 2020, 36(5): 797-805.
[9] NASTASOIU M, ISPAS N. Potential performance characteristics for different types of tractors: two-wheel-drive tractor, four-wheel-drive tractors and crawler tractors[C]∥The 4th International Congress of Automotive and Transport Engineering (AMMA 2018), 2018: 521-526.
[10] 匡文龙. 设施农业用遥控电动履带拖拉机的研发[D]. 南京:南京农业大学, 2020.KUANG Wenlong. Research and development of the remote-controlled electric crawler tractor for facility agriculture[D]. Nanjing: Nanjing Agricultural University, 2020. (in Chinese)
[11] 王元杰, 刘永成, 杨福增, 等. 温室微型遥控电动拖拉机的研制与试验[J]. 农业工程学报, 2012, 28(22): 23-29.WANG Yuanjie, LIU Yongcheng, YANG Fuzeng, et al. Development and test of tiny remotely controlled electric tractor for greenhouses[J]. Transactions of the CSAE, 2012, 28(22): 23-29. (in Chinese)
[12] 管春松, 胡桧, 陈永生, 等. 温室用小型电动拖拉机研究[J]. 中国农机化学报, 2015, 36(2): 67-69.GUANG Chunsong, HU Hui, CHEN Yongsheng, et al. Study on small electric tractors for greenhouse[J]. Journal of Chinese Agricultural Mechanization, 2015, 36(2): 67-69. (in Chinese)
[13] 吴腾飞. 小型遥控式履带拖拉机转向性能测试系统设计与试验[D]. 雅安:四川农业大学, 2019.WU Tengfei. Steering performance test system for small remote-controlled tracked tractor design and test[D]. Ya’an: Sichuan Agricultural University, 2019. (in Chinese)
[14] 王猛, 赵博, 王长伟, 等. 基于高斯混合模型的履带拖拉机转弯半径控制方法[J]. 农业机械学报, 2020, 51(增刊1): 557-563.WANG Meng, ZHAO Bo, WANG Changwei, et al. Method for controlling turning radius of crawler-type tractors based on GMM[J]. Transactions of the Chinese Society for Agricultural Machinery, 2020, 51(Supp.1): 557-563. (in Chinese)
[15] 杨福增, 牛瀚麟, 孙景彬, 等. 山地履带拖拉机与农具姿态协同控制系统设计与试验[J]. 农业机械学报, 2022, 53(1): 414-422.YANG Fuzeng, NIU Hanlin, SUN Jingbin, et al. Design and experiment of attitude cooperative control system of mountain crawler tractor and farm tools[J]. Transactions of the Chinese Society for Agricultural Machinery, 2022, 53(1): 414-422. (in Chinese)
[16] 毛智琳, 蒋建东, 章沈强, 等. 履带拖拉机液压控制差速转向系统设计与试验[J]. 农机化研究, 2022, 44(2): 253-258.MAO Zhilin, JIANG Jiandong, ZHANG Shenqiang, et al. Design and test of hydraulic control differential steering system for crawler tractor[J]. Journal of Agricultural Mechanization Research, 2022, 44(2): 253-258. (in Chinese)
[17] 孙景彬, 楚国评, 潘冠廷, 等. 遥控全向调平山地履带拖拉机设计与性能试验[J]. 农业机械学报, 2021, 52(5): 358-369.SUN Jingbin, CHU Guoping, PAN Guanting, et al. Design and performance test of remote control omnidirectional leveling hillside crawler tractor[J]. Transactions of the Chinese Society for Agricultural Machinery, 2021, 52(5): 358-369. (in Chinese)
[18] 王宝超, 乔明睿, 初香港, 等. 增程式电动履带拖拉机设计与试验[J]. 农业机械学报, 2023, 54(3): 431-439.WANG Baochao, QIAO Mingrui, CHU Xianggang, et al. Design and experiment on extended-range electric caterpillar tractor[J]. Transactions of the Chinese Society for Agricultural Machinery, 2023, 54(3): 431-439. (in Chinese)
[19] GUAN Z, LI Y, MU S, et al. Tracing algorithm and control strategy for crawler rice combine harvester auxiliary navigation system[J]. Biosystems Engineering, 2021, 211: 50-62.
[20] WU G, WANG G, BI Q, et al. Research on unmanned electric shovel autonomous driving path tracking control based on improved pure tracking and fuzzy control[J]. Journal of Field Robotic,2023, 40(7):1739-1753.
[21] HE Y, ZHOU J, SUN J, et al. An adaptive control system for path tracking of crawler combine harvester based on paddy ground conditions identification[J]. Computers and Electronics in Agriculture, 2023, 210: 107948.
[22] 吴明阳, 李小波, 代嘉惠, 等. 履带移动平台带边界层bang-bang路径跟踪控制[J]. 工矿自动化, 2021, 47(5): 88-94.WU Mingyang, LI Xiaobo, DAI Jiahui, et al. Path tracking control of crawler mobile platform based on bang-bang control with boundary layer[J]. Journal of Mine Automation, 2021, 47(5): 88-94. (in Chinese)
[23] 何永强, 周俊, 袁立存, 等. 基于履带式联合收获机转向特性的局部跟踪路径规划[J]. 农业机械学报, 2022,53(11): 13-21.HE Yongqiang, ZHOU Jun, YUAN Licun, et al. Local tracking path planning based on steering characteristics of crawler-type combine harvester[J]. Transactions of the Chinese Society for Agricultural Machinery, 2022,53(11): 13-21. (in Chinese)
[24] 董晓璇, 程嗣怡, 罗朝义, 等. 一种基于加权递推滤波的门限优化检测方法[J]. 现代雷达, 2019, 41(1): 19-25.DONG Xiaoxuan, CHENG Siyi, LUO Chaoyi, et al. A threshold optimization detection algorithm based on weighted recursive filter[J]. Modern Radar, 2019, 41(1): 19-25. (in Chinese)
[25] 李逃昌, 胡静涛, 高雷, 等. 基于模糊自适应纯追踪模型的农业机械路径跟踪方法[J]. 农业机械学报, 2013, 44(1): 205-210.LI Taochang, HU Jingtao, GAO Lei, et al. Agricultural machine path tracking method based on fuzzy adaptive pure pursuit model[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(1): 205-210. (in Chinese)
[26] 吕文杰, 马戎, 李岁劳, 等. 基于纯追踪模型的路径跟踪改进算法[J]. 测控技术, 2011, 30(7): 93-96.LÜ Wenjie, MA Rong, LI Suilao, et al. An improved algorithm based on pure pursuit model for path tracking[J]. Measurement &Control Technology, 2011, 30(7): 93-96. (in Chinese)