旋涡泵是一种依赖泵内的纵向旋涡进行能量传递的特殊类型叶片泵,因其小流量、高扬程、强自吸性能、气液混输等优点,被广泛应用于石化、航空航天、船舶及汽车等重要领域[1-2]。
旋涡泵内部流体以复杂的螺旋形轨迹运动,其主要依赖纵向旋涡进行叶轮与壳体流道之间流体的能量传递,纵向旋涡、轴向旋涡和径向旋涡联合作用,形成复杂的旋涡结构,复杂的旋涡结构在进行能量传递的同时引起大量的能量损失。纵向旋涡越强,叶轮内高能流体和侧流道内低能流体之间的动量交换越强烈,旋涡泵扬程越高。文献[3]研究发现M形流道可以诱导旋涡形成的同时缓解旋涡分离,使旋涡泵扬程和效率均有所提升。文献[4]研究发现泵内线性区纵向旋涡周期性的产生与消失使线性区压升占总压升的85.7%。文献[5]采用不同的涡识别方法对泵内的非定常涡流动进行对比,识别到纵向旋涡、轴向旋涡和径向旋涡3种典型的旋涡结构,认为叶轮内较多的轴向旋涡是导致旋涡泵低效率的原因。文献[6]对具有不同叶片角的旋涡泵进行研究,发现增加叶片角可以减少轴向旋涡,提升泵的性能。文献[7]对带有凸叶片的旋涡泵进行非定常流动特性研究,发现增加凸形叶片可以扩大泵的高效区,拓宽泵的应用范围。文献[8]通过λ2准则识别不同湍流模型下旋涡泵内的瞬态旋涡结构,认为旋涡结构在圆周方向上的演变是流体发生动量交换过程的原因。文献[9]将叶轮与泵壳流道的交界面和纵向旋涡中心之间的轴向距离以叶轮高度的1/2作为无量纲参考,认为无量纲化的轴向距离越小,叶轮与泵壳间的循环交换流动越剧烈,纵向旋涡强度越大,其性能也越优。文献[10]比较了不同平面涡量强度与熵损失和压力脉动的关系,认为动量交换速率受到叶轮中轴向和径向涡流的阻碍,叶轮产生最高的熵损失和压力脉动强度,导致了泵效率的降低。
现有研究虽然对旋涡泵内复杂旋涡结构的动态演化及能量损失进行了初步研究,但对泵内旋涡结构的量化统计及其引起的能量转换和能量损失研究存在不足。
本文综合使用Ω方法和Liutex方法对不同工况下旋涡泵叶轮和侧流道内的旋涡结构进行识别和强度表征,从而进行定性分析,然后通过旋涡体积比和平均旋涡强度对旋涡的体积和强度进行量化,最后通过动能方程的涡动力学分解式和涡量分解理论对旋涡结构引起的能量转换和能量损失的影响规律进行分析。
以CLDB240-768型旋涡泵为研究对象,设计流量Q0为20 m3/h,额定扬程H0为50 m,额定转速n0为1 450 r/min,其叶轮和侧流道的几何结构如图1所示。旋涡泵的叶轮为开式叶轮,叶轮外径d2为240 mm,叶轮内径d1为150 mm,叶片宽度b为18 mm,叶片厚度b1为7.36 mm,叶片数z为24,轴向间隙S1和径向间隙S2均为0.2 mm,侧流道为闭式向心流道,侧流道外径d4为258 mm,侧流道内径d3为168 mm,侧流道高度t0为17.8 mm,包角φ为30°。
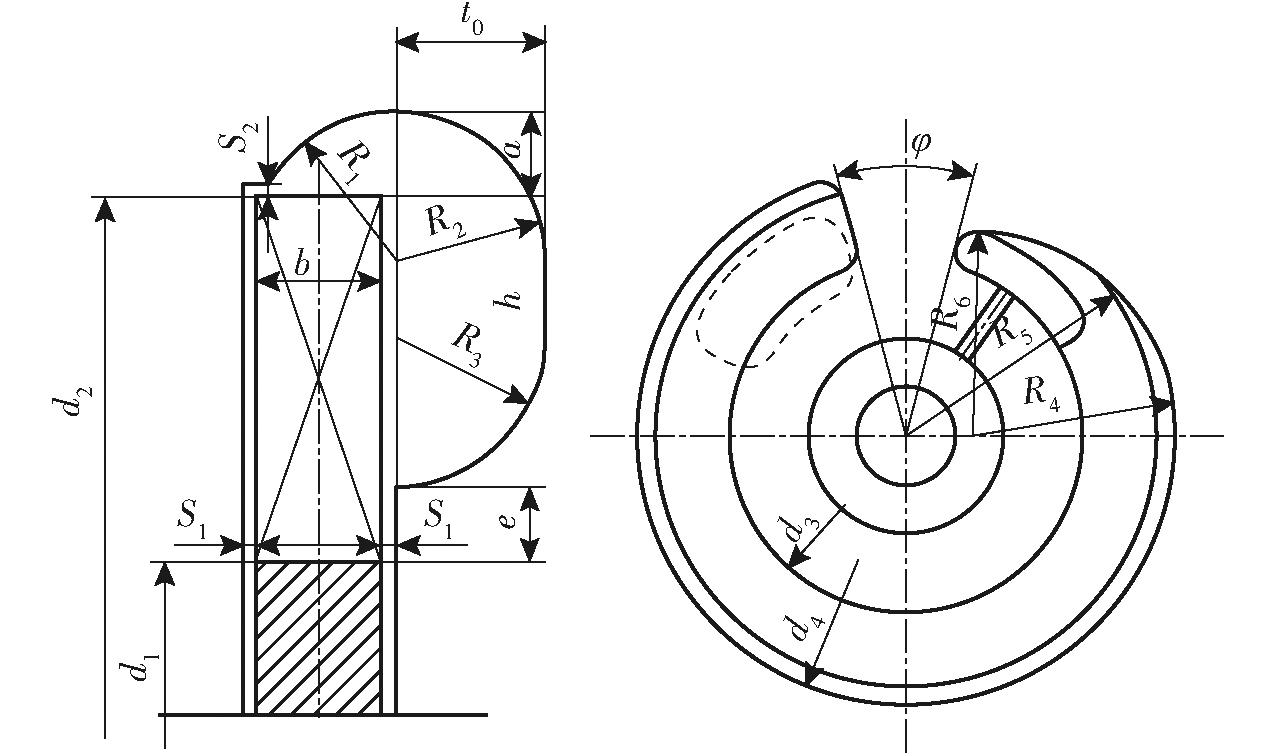
图1 旋涡泵叶片和侧流道轴面图
Fig.1 Axial projection draw of impeller and side channel
旋涡泵整体计算域由进口管、吸入口、叶轮及间隙、侧流道、出水段和出口管6部分组成,如图2所示。
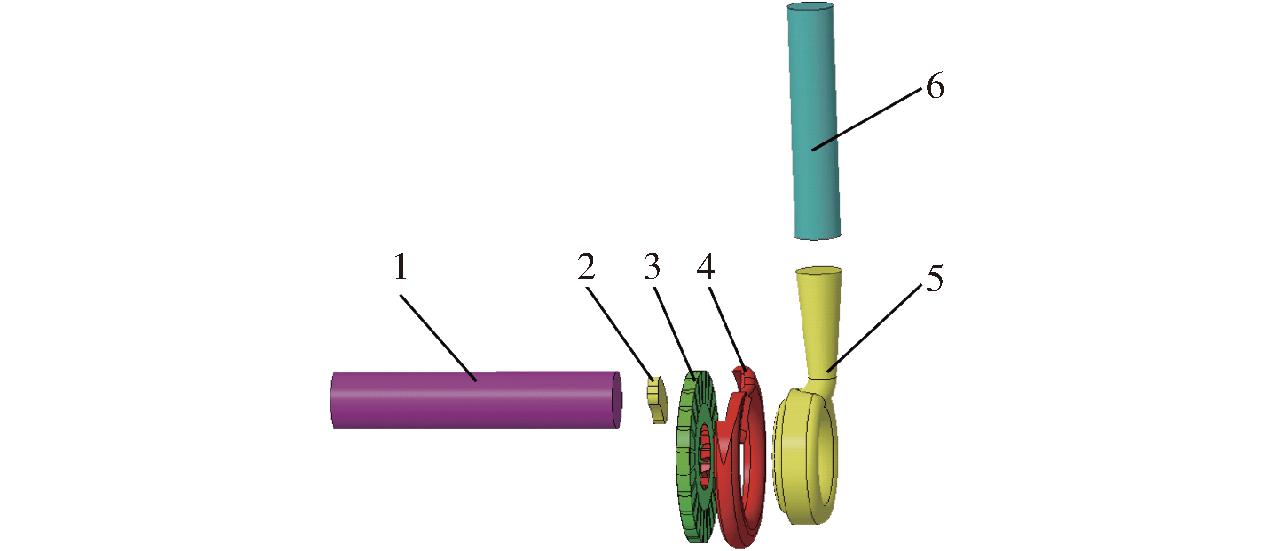
图2 旋涡泵各流体域示意图
Fig.2 All fluid domains of vortex pump
1.进口管 2.吸入口 3.叶轮及间隙 4.侧流道 5.出水段 6.出口管
计算域全部采用六面体结构化网格,壁面区域进行边界层网格处理,对叶顶间隙和侧流道尖角的部分区域进行局部加密,如图3所示。
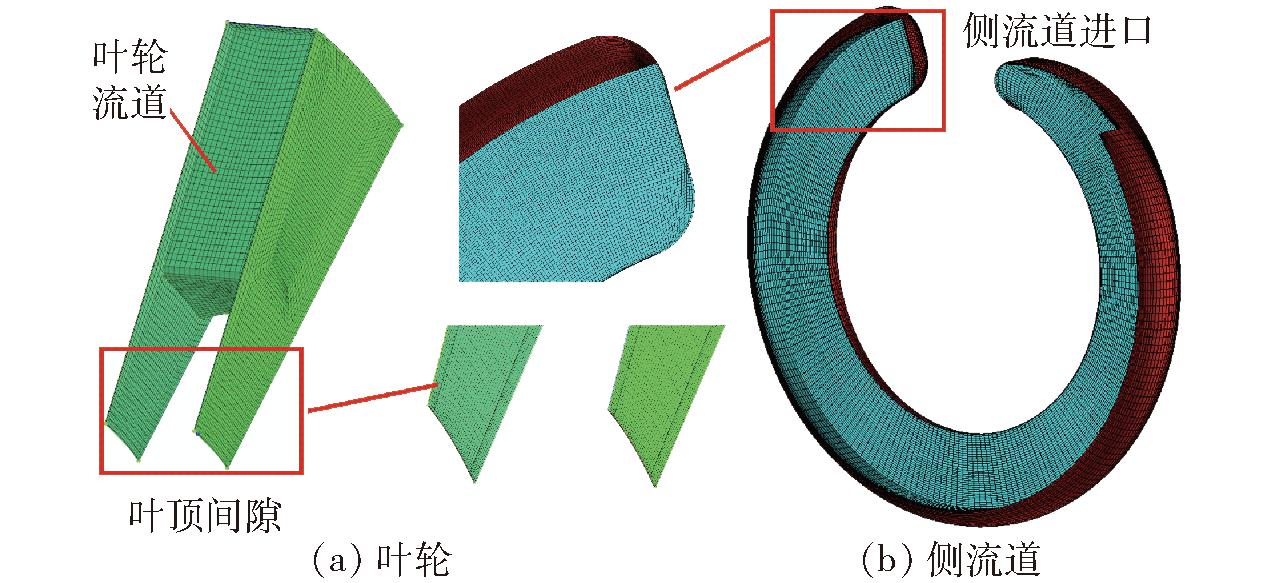
图3 叶轮和侧流道网格划分细节
Fig.3 Grid details of impeller and side channel
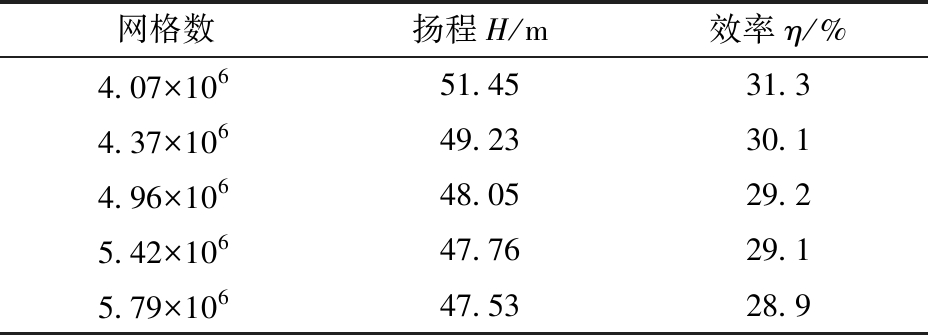
在额定工况下对该旋涡泵进行网格无关性检查,如表1所示,当网格数大于4.96×106时,旋涡泵扬程和效率趋于稳定,此时获得最经济的网格数。
表1 网格无关性检查
Tab.1 Grid independence check
网格数扬程H/m效率η/% 4.07×10651.4531.34.37×10649.2330.14.96×10648.0529.25.42×10647.7629.15.79×10647.5328.9
研究表明SST k-ω模型对旋涡泵内流动的数值模拟具有较好的适应性[11],本研究采用SST k-ω湍流模型。在定常计算结果的基础上进行非定常数值模拟迭代求解,非定常计算的时间步长Δt为0.000 114 9 s(叶轮旋转1°),叶轮共计旋转6圈后计算结果趋于稳定,总时间T为0.248 s,取稳定后的最后一圈结果进行分析。进口边界条件设为质量流量进口,出口设为压力出口。采用无滑移壁面边界条件,近壁面采用标准壁面函数。压力与速度耦合采用SIMPLEC算法,采用二阶迎风格式离散基本方程组进行迭代求解,收敛精度设定为10-5。
旋涡泵性能实验台如图4所示,由储水罐、管路、被试泵、动力及控制系统组成。进口管路上依次安装有调节阀、真空表,出口管路上依次安装有压力表、涡轮流量计、调节阀等。

图4 旋涡泵实验系统
Fig.4 Experimental system of vortex pump
1.储水罐 2.进口阀 3.进口真空表 4.电机 5.旋涡泵 6.出口压力表 7.流量计 8.出口阀
数值模拟和实验结果对比如图5所示,数值模拟值与实验值比较接近,额定工况点实验效率有最大值,与数值模拟值的误差为0.65%。实验过程中,流量偏大时,旋涡泵进口存在一定的空化,轴功率波动增大,且数值模拟未考虑轴向力平衡装置的流量泄漏,导致数值模拟的泵效率与实验值误差在大流量时较大。
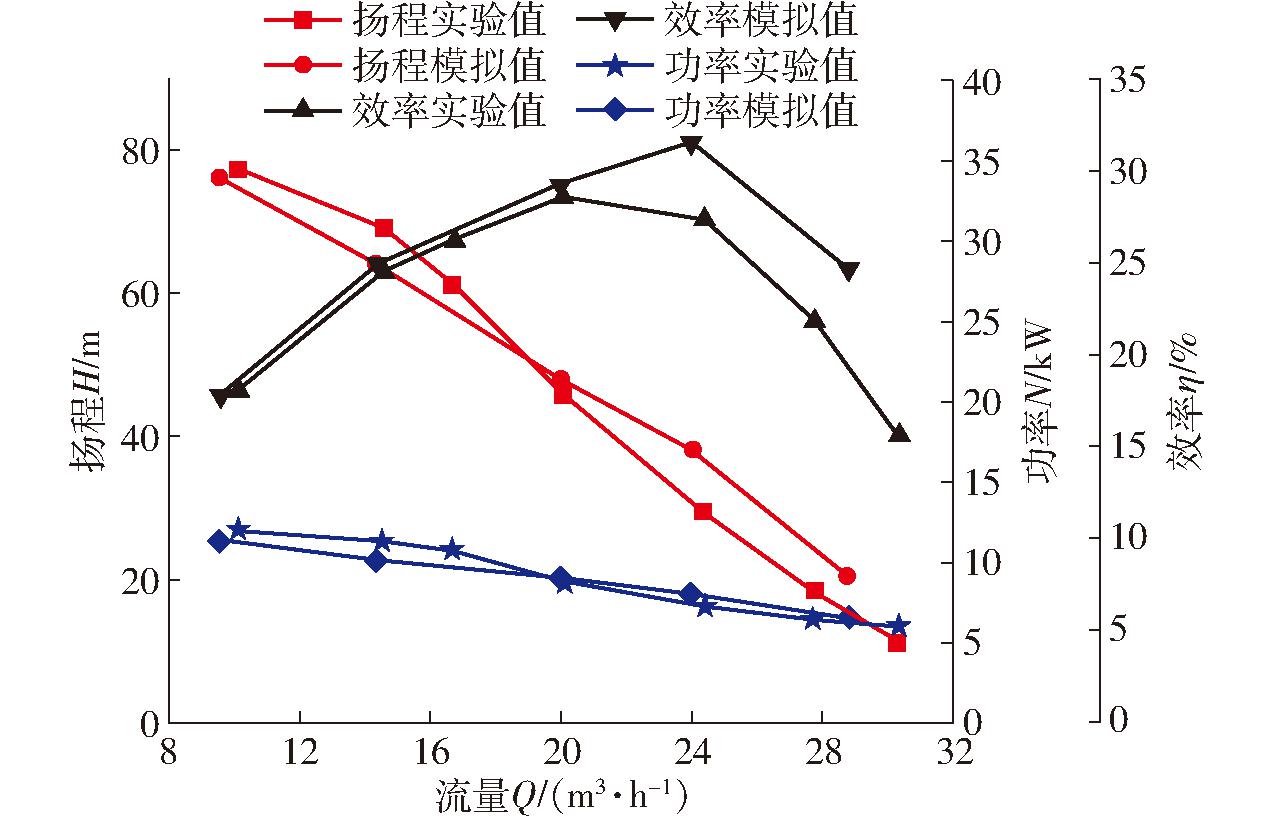
图5 旋涡泵数值模拟及实验性能对比
Fig.5 Numerical simulation and experimental performance comparison of vortex pump
Ω方法[12]将Ω定义为旋转部分的涡量占总涡量的比值,相当于涡浓度的概念,其表达式为Ω=(‖B‖F)2/((‖A‖F)2 +(‖B‖F)2+ε),其中‖·‖F表示矩阵的Frobenius范数,A和B分别为速度梯度张量![]() 的对称张量和反对称张量。ε=δ((‖B‖F)2 -(‖A‖F)2)max,为趋于0的正数,确保分母非零,本研究δ取值为10-6。
的对称张量和反对称张量。ε=δ((‖B‖F)2 -(‖A‖F)2)max,为趋于0的正数,确保分母非零,本研究δ取值为10-6。
Ω作为无量纲数,对阈值不敏感,当Ω大于0.5时表示旋转部分的涡量占优,即当旋转力强于应变力时将形成旋涡,一般选择Ω=0.52可以同时捕捉到流场中的强弱涡结构,为了避免剪切层干扰,本研究选定Ω=0.56进行涡识别。
Liutex涡矢量方法[13]提出了一个基于特征向量的旋涡矢量R。该方法将涡量ω分解为刚体转动部分和非转动部分,即![]() 其中R为旋涡矢量,
其中R为旋涡矢量,![]() 式中ω是涡量,r是
式中ω是涡量,r是![]() 的实特征向量,λci表示
的实特征向量,λci表示![]() 的复特征值的虚部。R的大小是当地流体旋转角速度的两倍,即流体旋转强度,其方向由速度梯度矩阵实特征向量确定,可以同时表示旋涡旋转强度和旋转方向。
的复特征值的虚部。R的大小是当地流体旋转角速度的两倍,即流体旋转强度,其方向由速度梯度矩阵实特征向量确定,可以同时表示旋涡旋转强度和旋转方向。
为了同时表示旋涡结构的位置和旋涡强度的大小,通过Liutex方法中R对不同工况下Ω方法识别的叶轮和侧流道内旋涡结构等值面进行着色,其中小流量为0.7Q0 工况,大流量为1.4Q0工况。
从图6可以看出,叶轮流道和叶顶间隙充满了复杂的旋涡结构,这些复杂流动结构与叶片正反面压差的存在有关,将会对泵内流动损失和流动稳定性产生较大影响[14-15]。随着流量的增大,叶轮流道内的旋涡结构体积明显减小,占据流道中部和根部的旋涡结构逐渐向叶片吸力面运动,靠近轮缘处的旋涡结构变化较小,间隙内旋涡结构分布区域明显变大。
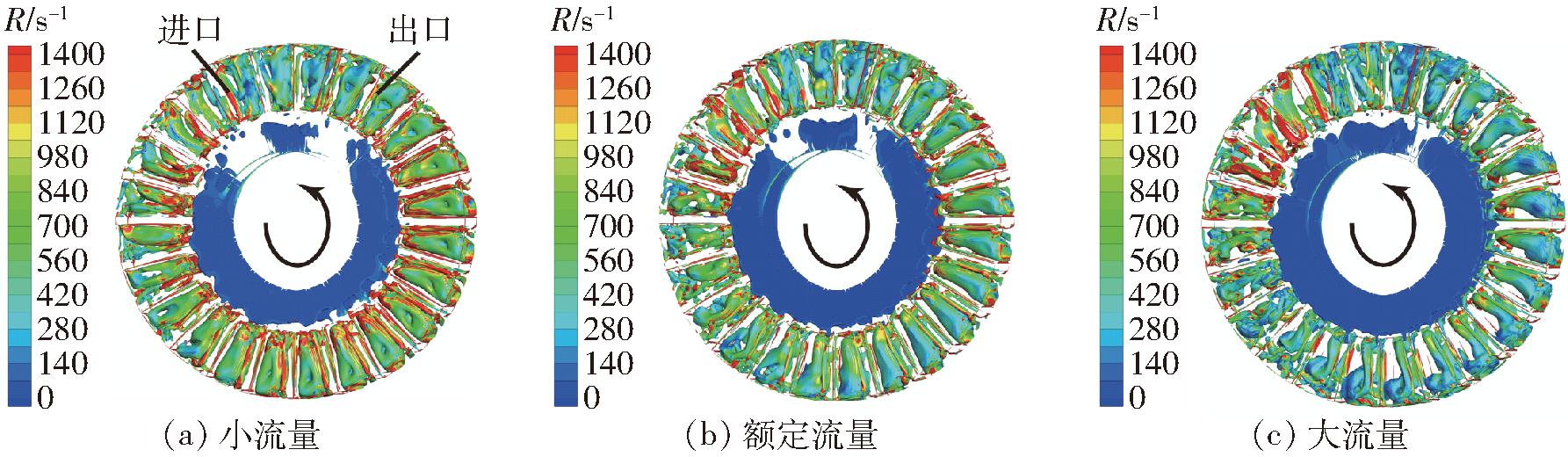
图6 不同工况下Ω方法识别的叶轮内旋涡结构
Fig.6 Vortex structure in impeller identified by Ω method under different working conditions
旋涡强度方面,高强度旋涡结构分布在叶轮进出口位置、叶轮根部和旋涡充分发展区域。随着流量的增大,进出口速度增大,旋涡强度增大;随着流量的增大,叶轮与流道壳体间的流速差降低,旋涡充分发展区域旋涡强度减小。
从图7可以看出,流量越小,侧流道内清晰且稳定的涡管结构形成得越早,数量也越多,这些涡管结构主要分布在旋涡充分发展区域,近似呈螺旋结构。这些螺旋的管状旋涡从轮缘处流出,沿侧流道圆周方向和纵向运动的同时不断向后拉伸至其他叶轮流道对应的侧流道内径处,最终与其他旋涡结构相互作用之后再次进入叶轮流道内。
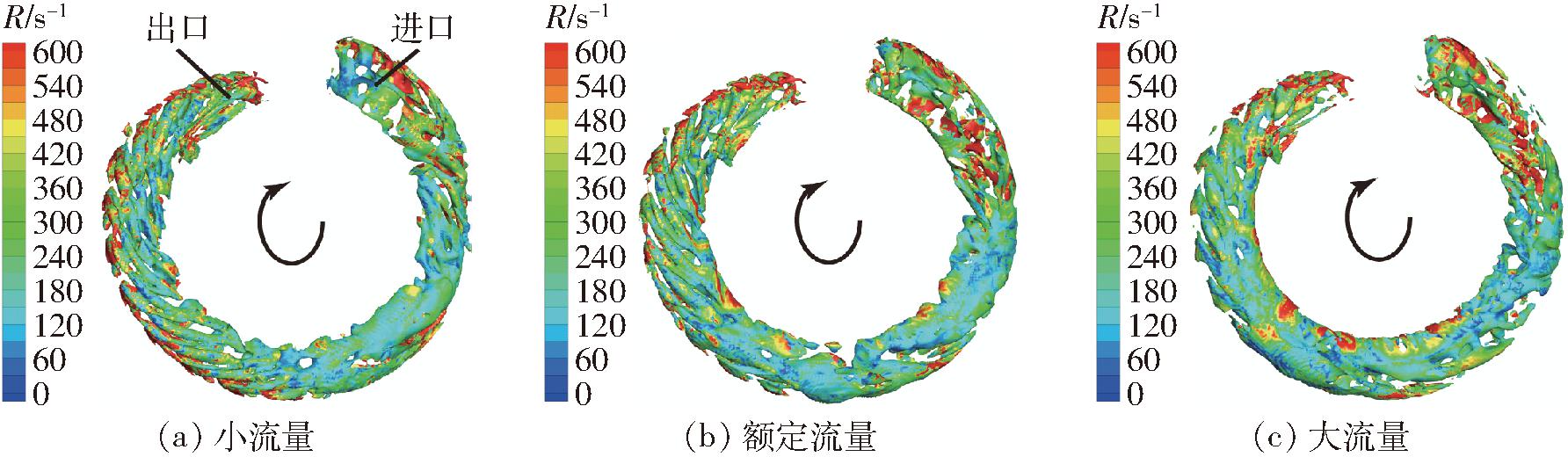
图7 不同工况下Ω方法识别的侧流道内旋涡结构
Fig.7 Vortex structure in side channel identified by Ω method under different working conditions
旋涡强度方面,高强度旋涡结构主要分布在侧流道进出口和旋涡充分发展区域。随着流量的增大,进出口速度增大,旋涡强度增大;随着流量的增大,叶轮与流道壳体间的流速差降低,纵向旋涡强度减弱,旋涡充分发展区域的旋涡强度减小。对比图6可以看出,叶轮内旋涡强度明显大于相同工况下的侧流道内。
通过将Ω方法投影到轴向[16]来识别叶轮流道内的轴向旋涡结构,如图8所示。从图8可以看出,叶轮内轴向旋涡主要分布在叶片根部和靠近轮缘处,随着流量的增大,轮缘处旋涡体积增大。
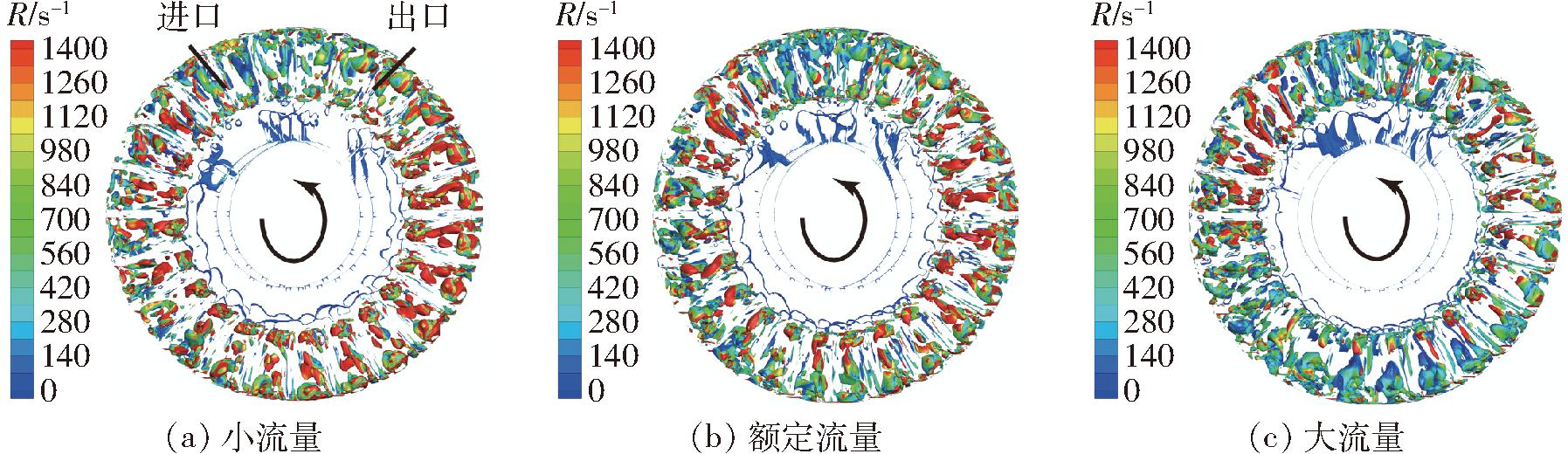
图8 不同工况下Ω方法识别的叶轮内轴向旋涡结构
Fig.8 Axial vortex structure in impeller identified by Ω method under different working conditions
旋涡强度方面,高强度旋涡主要分布在叶轮进出口位置,叶片根部和旋涡充分发展区域。随着流量的增大,旋涡充分发展区域的旋涡强度从轮缘至轮毂逐渐减小。
进一步通过旋涡体积比和平均旋涡强度对旋涡泵叶轮和侧流道内识别的旋涡结构体积和强度进行量化研究。
旋涡体积比可以直观地量化区域内的旋涡体积,便于分析不同位置的旋涡状态的改变[17]。本研究主要考虑叶轮内旋涡体积比(叶轮内Ω方法等值面包裹的网格单元体体积占叶轮水体体积百分比)和侧流道内旋涡体积比(侧流道内Ω方法等值面包裹的网格单元体体积占侧流道水体体积百分比),结果如图9所示。
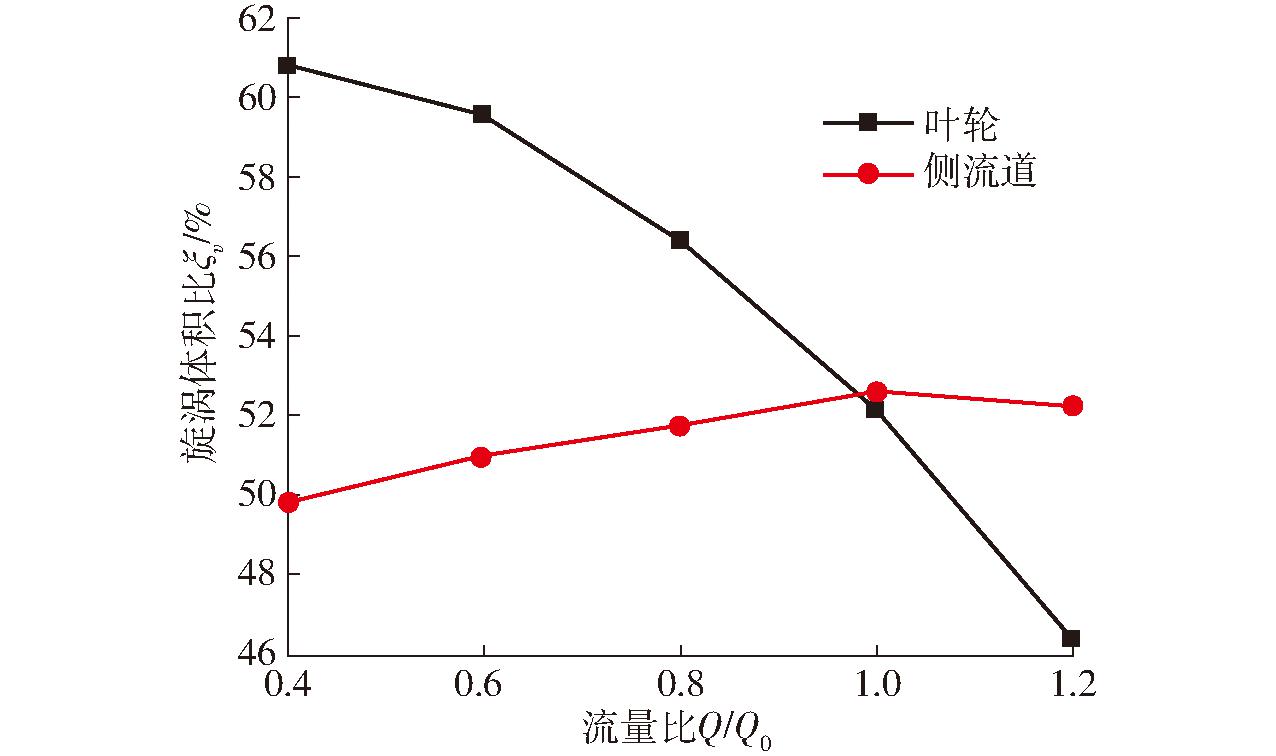
图9 不同工况下叶轮和侧流道内旋涡体积比
Fig.9 Vortex volume ratio in impeller and side channel under different working conditions
从图9可以看出,随着流量的增大,叶轮内旋涡体积比不断减小,从0.4Q0工况时的60.78%减小到1.2Q0工况时的46.36%,减少14.42个百分点。侧流道内的旋涡体积比变化幅度相对较小。这证明了随着流量的增大,叶轮流道内的旋涡体积会不断减小,侧流道内则变化较小。
除了旋涡体积比,旋涡强度对性能的影响也很重要。为定量评价不同工况下旋涡泵叶轮和侧流道内的旋涡强度,提出平均旋涡强度L,公式为
(1)
式中 |Ri|——第i组旋涡强度,s-1
V|Ri|——第i组旋涡体积,m3
Vtot——旋涡总体积,m3
其中n表示将计算域内的旋涡(Ω≥0.56)按照强度即Liutex值的大小|R|均分为n组进行分析,n为整数且n越大,L的计算结果越精确,根据计算经验建议n≥50,本研究n取50,不同范围的旋涡强度|Ri|的取值范围根据Liutex方法识别的该区域旋涡的Liutex值范围来确定,本研究旋涡泵叶轮内旋涡强度为0~5 000 s-1,则第1组旋涡强度范围为0<|R1|≤100,第2组旋涡强度范围为100<|R2|≤200,以此类推,第n组旋涡强度范围为4 900<|R50|≤5 000,计算时|Ri|取第i组的上限端点值,结果如图10所示。

图10 不同工况下叶轮和侧流道内平均旋涡强度
Fig.10 Average vortex intensity in impeller and side channel under different working conditions
从图10可以看出,叶轮内平均旋涡强度都明显大于相同工况下侧流道内平均旋涡强度。图9和图10的变化趋势基本一致,即叶轮内旋涡体积比和平均旋涡强度都随着流量的增大而逐渐减小,从0.4Q0工况时的2 002 s-1减小到1.2Q0工况时的1 374 s-1,减小31.37%,侧流道内则变化较小。这证明了随着流量的增大,叶轮流道内旋涡强度会不断减小,侧流道内则变化较小。
对比图9、10可以看出,平均旋涡强度与旋涡体积相关性较强,大流量工况下,叶轮旋涡体积比小于侧流道,而其平均旋涡强度远大于侧流道,这说明叶轮内高强度旋涡对总旋涡的占比远大于侧流道内。
为研究不同工况下泵内复杂旋涡结构所引起的能量交换和能量损失,引入流体动能方程的涡动力学分解式[18-21]进行分析,对于不可压缩流体,表达式为
(2)
式中 ρ——流体密度,kg/m3
E——流体动能,J
t——时间,s P——压力,Pa
μ——粘性系数,Pa·s
等式右边第1项表示压力梯度对流体的做功,称为压力推进功。等式右边第2项为Lamb矢量散度,是涡量和速度对粘性流体的综合影响,它体现了旋涡力对动能产生的输运作用[22]。等式右边第3项为拟涡能项,是流体涡量引起的粘性耗散作用。
图11为不同工况下叶轮和侧流道的压力推进功的体积积分值。从图11可以看出,叶轮内的压力推进功都为负值,说明叶轮对流体做功,使总动能增加,侧流道内的压力推进功都为正值,说明侧流道内流体总动能减少。叶轮内压力推进功的绝对值随着流量的增大而减小。

图11 叶轮和侧流道内压力推进功体积积分值
Fig.11 Volume integral values of pressure propulsion power in impeller and side channel
图12为不同工况下叶轮和侧流道轴向截面的压力推进功分布。可以看出,每个叶轮流道内都存在压力推进功,且靠近吸力面侧为正值,靠近压力面侧为负值。随着流量的增大,压力推进功绝对值不断减小且向叶片吸力面移动。

图12 不同工况下叶轮和侧流道轴向截面压力推进功
Fig.12 Pressure propulsion power of impeller and side channel under different working conditions
侧流道内压力推进功主要出现在进出口和旋涡充分发展区域。随着流量的增大,进出口速度增大,压力推进功绝对值变大;随着流量的增大,叶轮与壳体间的流速差降低,压力梯度减小,旋涡充分发展区域的压力推进功绝对值减小。
图13为不同工况下叶轮和侧流道内的Lamb矢量散度的体积积分值。通过Lamb矢量散度可以描述高低动量流体之间的动量交换[22],其正值表示以应变运动为主的动量输运;负值表示以涡量承载运动为主的动量输运。
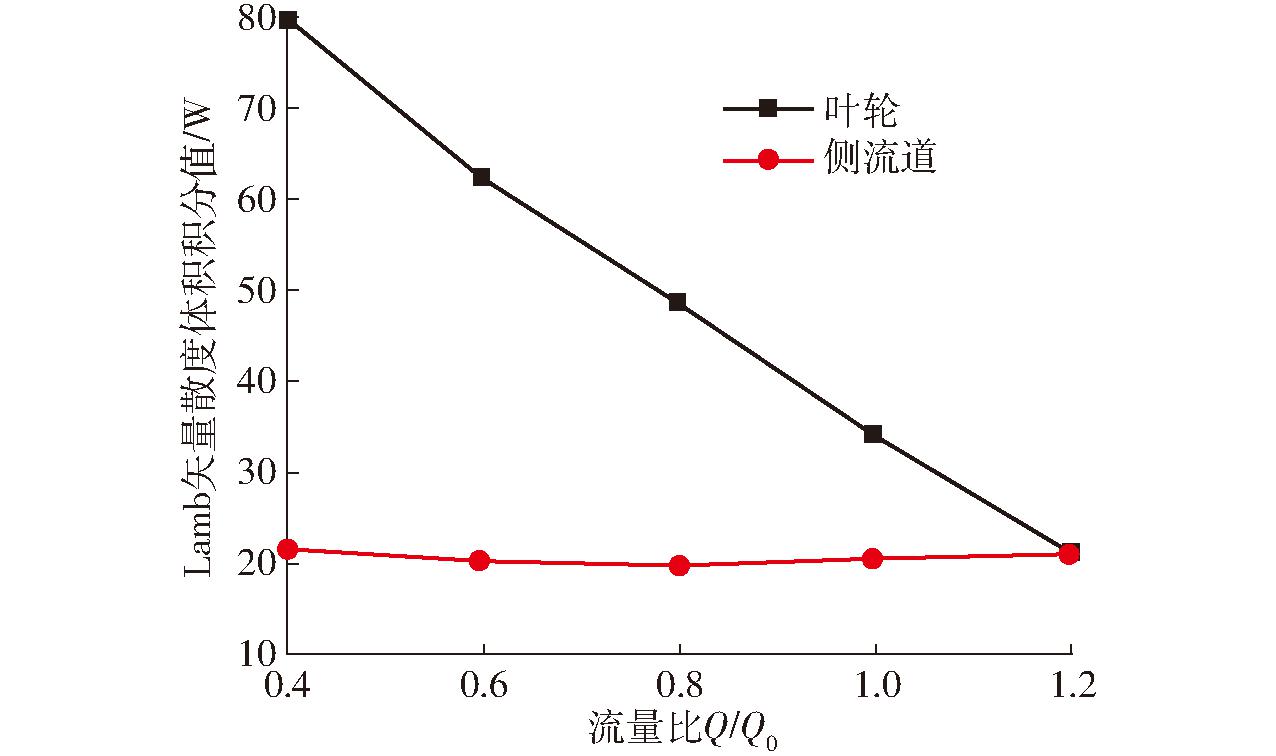
图13 叶轮和侧流道内Lamb矢量散度的体积积分值
Fig.13 Volume integral values of Lamb vector divergence in impeller and side channel
从图13可以看出,叶轮和侧流道内的Lamb矢量散度的体积积分都为正值,这说明总体上叶轮和侧流道内的动量输运以应变运动为主。随着流量的增大,叶轮内旋涡强度降低,总涡量减小,Lamb矢量散度减小,侧流道内则变化不大。
为准确分析旋涡结构对能量转换和能量损失的影响,引入涡量分解理论将总涡量ω进一步分解为刚性涡量ωR和变形涡量ωS,刚性涡量ωR也就是Liutex方法中的旋涡矢量R,可用于表征流体微团的刚性旋转运动,即旋涡强度的大小,变形涡量ωS则反映诱导旋涡运动的剪切效应。通过体积积分可求得不同工况下旋涡泵叶轮和侧流道内总涡量和刚性涡量的积分值[23],进一步得到刚性涡量和变形涡量对总涡量的占比,如图14所示。
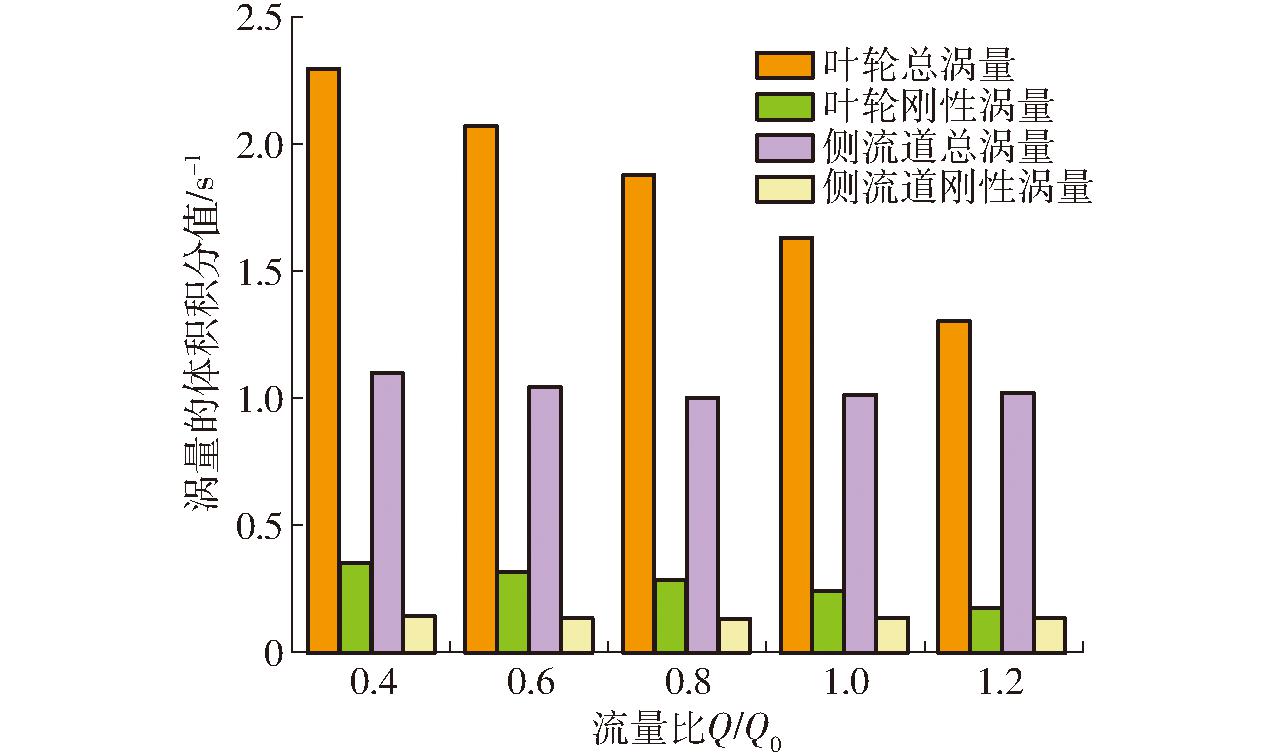
图14 叶轮和侧流道内涡量的体积积分值
Fig.14 Volume integral value of vorticity in impeller and side channel
从图14可以看出,随着流量的增大,积分得到的叶轮内总涡量和总刚性涡量都减小,而其在侧流道内变化较小。叶轮和侧流道内刚性涡量对总涡量的占比都较小,这说明总涡量中主要以变形涡量为主导,变形涡量对总涡量的占比更大。
图15为不同工况下叶轮中间截面刚性涡量和Lamb矢量散度分布。从图15可以看出,Lamb矢量散度负值主要出现在刚性涡量较大的区域,正值主要位于叶片壁面及叶轮进口。随着流量的增大,叶轮与流道壳体间的流速差降低,旋涡强度减小,Lamb矢量散度负值影响的动量交换区域明显减小且向叶片吸力面移动。
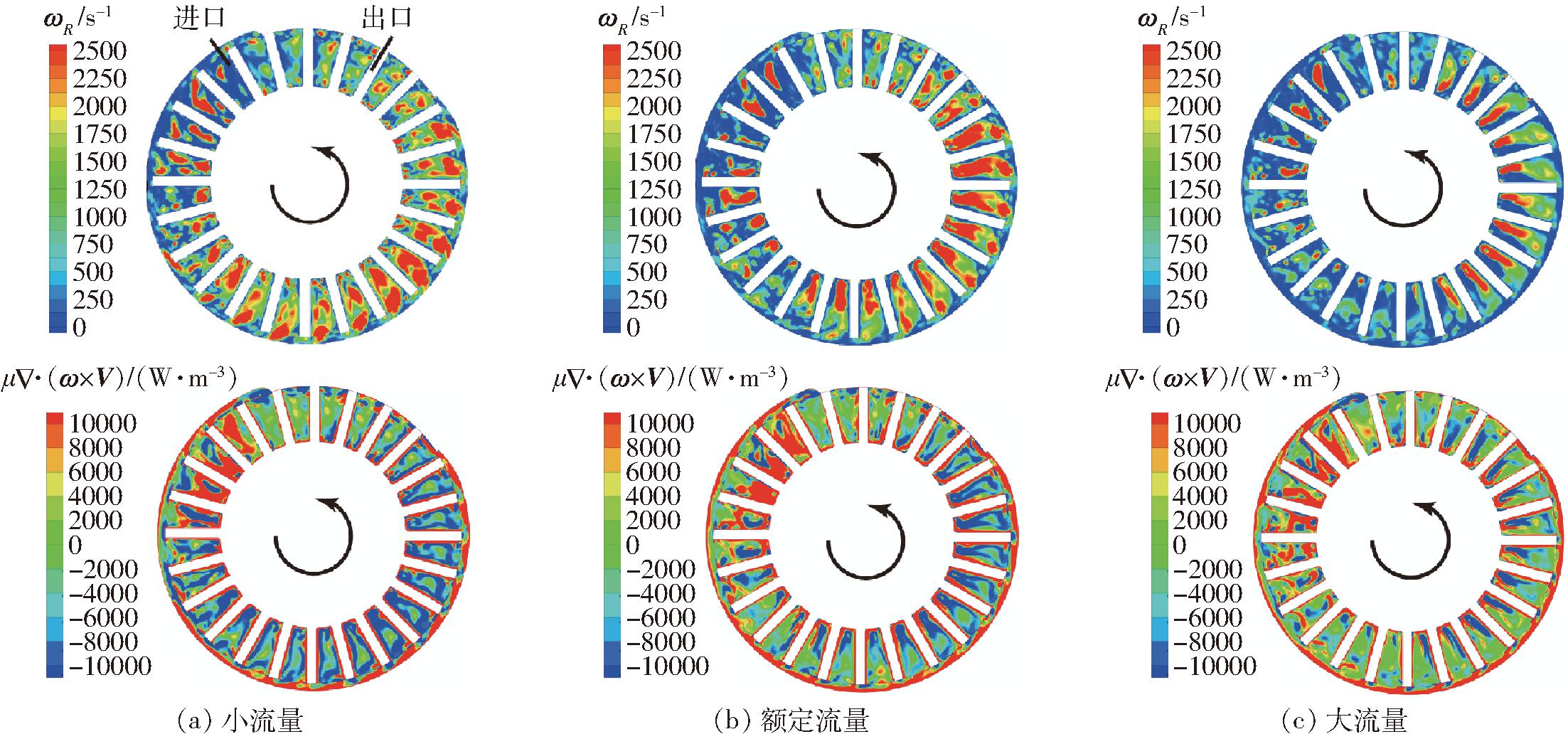
图15 不同工况下叶轮中间截面刚性涡量和Lamb矢量散度
Fig.15 Rigid vorticity and Lamb vector divergence of impeller under different working conditions
图16为不同工况下侧流道轴向截面刚性涡量和Lamb矢量散度分布。从图16可以看出,侧流道内的刚性涡量和Lamb矢量散度具有较强的相关性,旋涡充分发展区域的刚性涡量较大值和Lamb矢量散度的负值都近似为螺旋形,与旋涡结构一致。
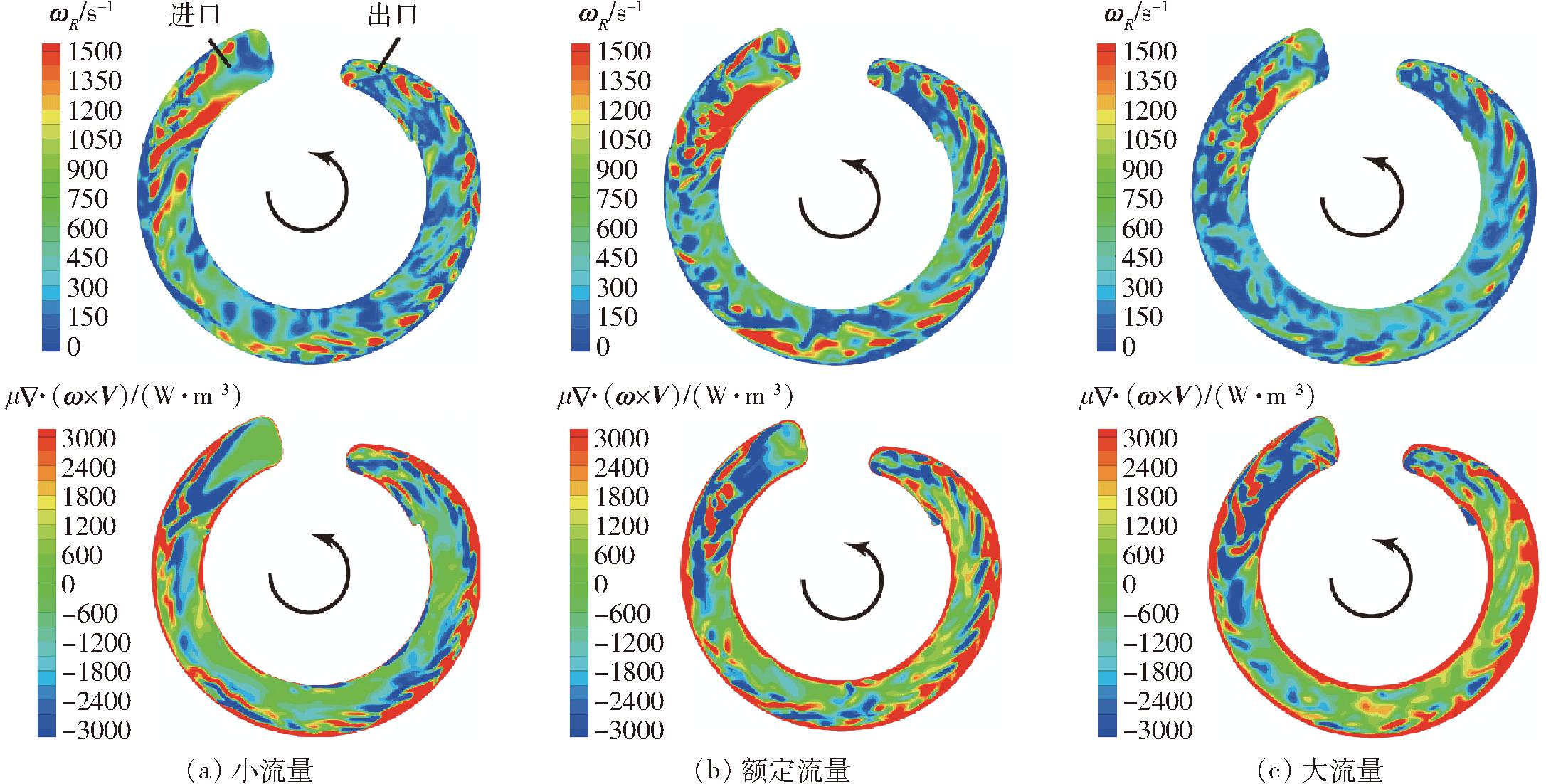
图16 不同工况下侧流道轴向截面刚性涡量和Lamb矢量散度
Fig.16 Rigid vorticity and Lamb vector divergence of side channel under different working conditions
正负值交替的双层结构的Lamb矢量散度分布能够反映动量交换的过程[24]。侧流道内Lamb矢量散度正负值交替主要出现在旋涡充分发展区域。如图16所示,小流量工况时,侧流道内正负值交替形成的较早且散度较大,说明动量交换强烈,但该工况的散度分布较为混乱,排列边界并不清晰,对动量交换效率有不利影响;大流量工况时,散度为负,即涡量运动主导的动量交换明显减少,这是因为流量的增大使纵向旋涡的强度减小,动量交换减弱。
从图17可以看出,相同工况下叶轮内拟涡能体积积分值远大于侧流道内,这是因为相同工况下叶轮内的总涡量较大,对动能产生的耗散作用也较大。所以叶轮内产生的水力损失远大于侧流道内产生的水力损失。随着流量的增大,涡量不断减小,因此叶轮内的拟涡能值减小。
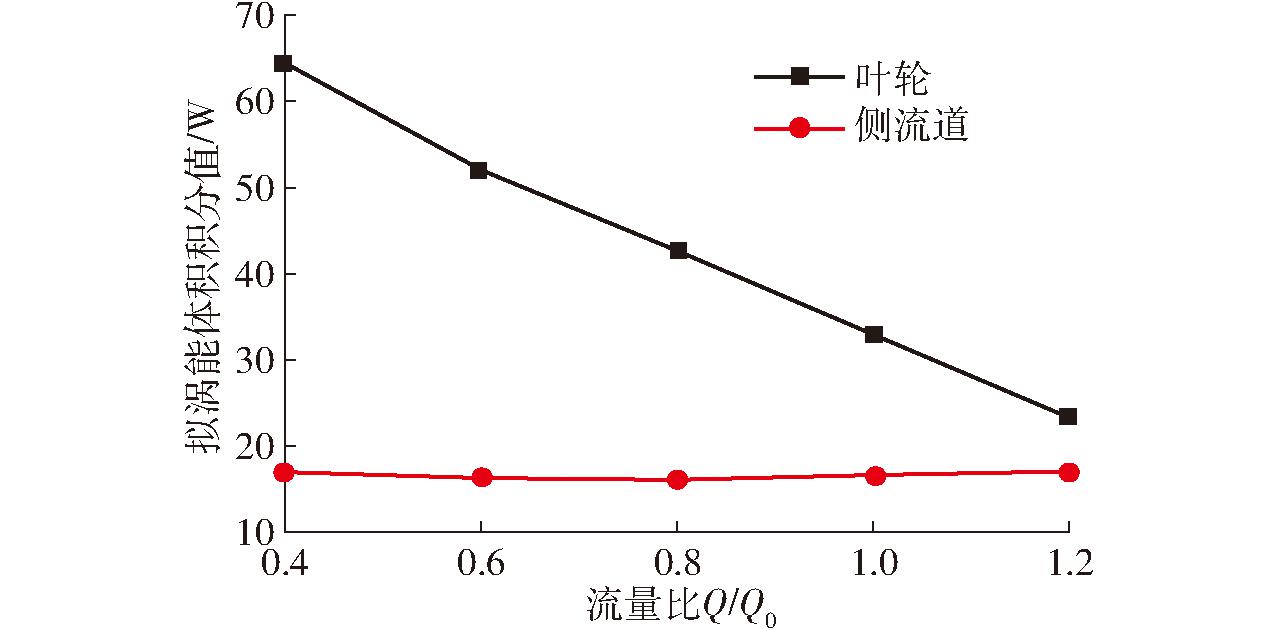
图17 叶轮和侧流道内拟涡能的体积积分值
Fig.17 Volume integral values of enstrophy in impeller and side channel
从图18可以看出,拟涡能较大值主要分布在叶轮进口、叶片壁面及叶根。变形涡量和拟涡能耗散损失相关性较强,分布区域基本一致,这与变形涡量对总涡量的占比较高有关[25],由于刚性涡量对总涡量的占比较小,其产生的拟涡能较小,相关性也较小。
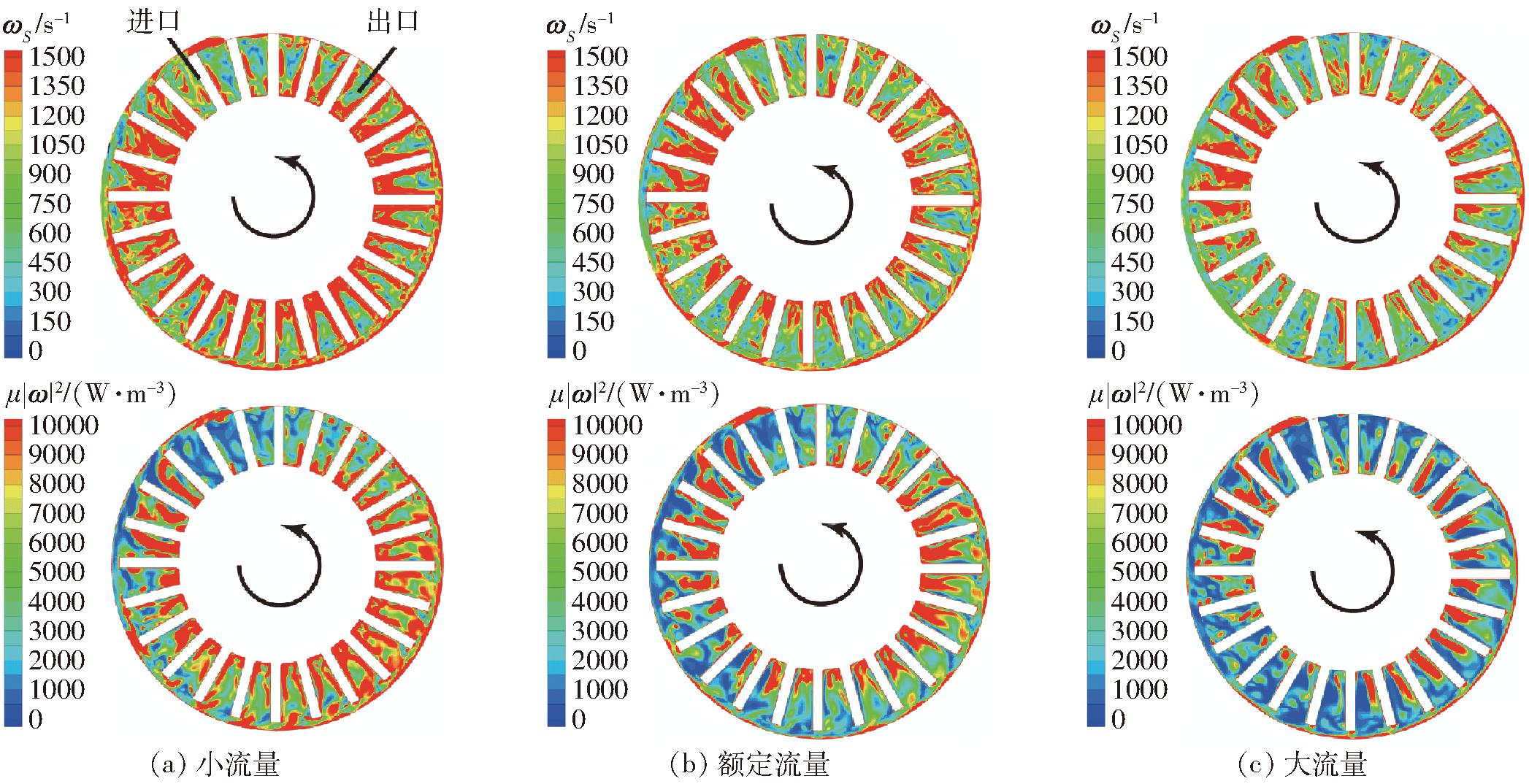
图18 不同工况下叶轮中间截面变形涡量和拟涡能
Fig.18 Deformational vorticity and enstrophy of impeller under different working conditions
从图19可以看出,侧流道内变形涡量和拟涡能同样具有较强的相关性。侧流道内拟涡能较大值主要分布在侧流道进口,流道壁面及旋涡充分发展区域。随着流量的增大,进口拟涡能值变大,旋涡充分发展区域的拟涡能值变小。
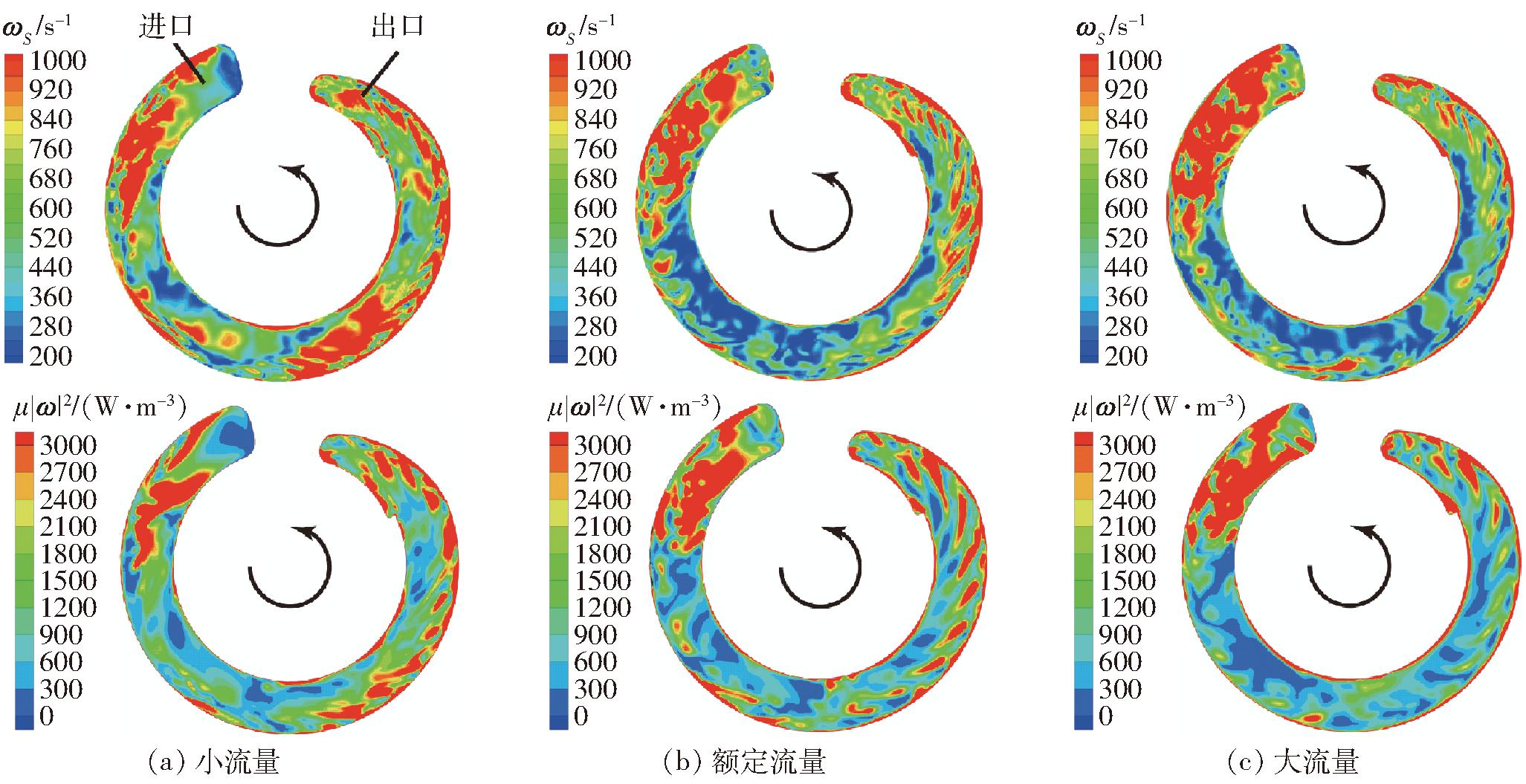
图19 不同工况下侧流道轴向截面变形涡量和拟涡能
Fig.19 Deformational vorticity and enstrophy of side channel under different working conditions
对比图11、13、17可知,压力推进功即压力梯度的做功对流体动能的贡献最大,与涡量场相关的Lamb矢量散度代表的动量转换和拟涡能代表的耗散损失占比较小,由于刚性涡量对总涡量的占比较小,因此旋涡结构引起的动量输运及耗散损失占比更小。
对比图15、16、18、19可知,刚性涡量即旋涡强度和Lamb矢量散度具有较强的相关性,变形涡量和拟涡能具有较强的相关性。这说明虽然刚性涡量对总涡量的占比较小,但其对流场内的动量输运影响较大,其与动量输运过程正相关,而变形涡量代表的剪切效应则对耗散损失影响较大。
(1)旋涡泵内的旋涡充分发展区域存在螺旋形的管状旋涡结构,该旋涡从叶轮流道流出,沿轮缘进入侧流道内,随着流量的增大,叶轮与流道壳体间的流速差降低,螺旋形涡管数量减少且旋涡强度降低。
(2)基于旋涡体积比和平均旋涡强度可以对旋涡泵内旋涡结构的体积和强度进行量化研究。流量的增大使得叶轮内旋涡体积和强度都不断减小,侧流道内变化较小。相同工况下叶轮内平均旋涡强度明显大于侧流道内。
(3)压力梯度对流体动能的贡献最大,旋涡引起的动量输运及耗散损失占比较小。刚性涡量即旋涡强度对总涡量占比较小,其与动量输运过程正相关,变形涡量对总涡量占比较大,其与拟涡能耗散损失相关性较强。
[1] 贾宗谟.旋涡泵 液环泵 射流泵[M].北京:机械工业出版社,1993.
[2] 关醒凡.现代泵理论与设计[M].北京:中国宇航出版社,2011.
[3] 王洋,李亚成,曹璞钰,等.M型截面流道对旋涡泵性能的影响分析[J].农业机械学报,2014,45(3):77-82.WANG Yang,LI Yacheng,CAO Puyu, et al. Effects of channel with M-type section on the performance of vortex pump[J].Transactions of the Chinese Society for Agricultural Machinery,2014,45(3):77-82. (in Chinese)
[4] 陶佳欣,陈万强,李祥阳.旋涡泵内纵向旋涡影响机理分析[J].流体机械,2018,46(8):49-55. TAO Jiaxin,CHEN Wanqiang,LI Xiangyang. Analysis of the longitudinal vortex effect mechanism in vortex pump[J]. Fluid Machinery,2018,46(8):49-55. (in Chinese)
[5] ZHANG F, APPIAH D, CHEN K, et al. Dynamic characterization of vortex structures and their evolution mechanisms in a side channel pump[J]. ASME Journal of Fluids Engineering, 2020, 142(11): 111502.
[6] ZHANG F, APPIAH D, ZHANG J, et al. Transient flow characterization in energy conversion of a side channel pump under different blade suction angles[J]. Energy, 2018, 161: 635-648.
[7] 张帆,魏雪园,陈轲,等.带凸形叶片侧流道泵内部旋涡特性研究[J].农业机械学报,2020,51(3):115-122. ZHANG Fan,WEI Xueyuan,CHEN Ke, et al. Internal vortex characteristics of side channel pump with convex blade[J]. Transactions of the Chinese Society for Agricultural Machinery,2020,51(3):115-122. (in Chinese)
[8] WANG Y F, ZHANG F, YUAN S Q, et al. Effect of URANS and hybrid RANS-large eddy simulation turbulence models on unsteady turbulent flows inside a side channel pump[J]. Journal of Fluids Engineering, 2020, 142(6):061503.
[9] LI Q Q, WU C S, QIAN B, et al. Investigation of the matching relation between impeller and flow channel of regenerative flow pumps[J]. Journal of Fluids Engineering, 2021, 143(6): 061209.
[10] ZHANG F, APPIAH D, CHEN K, et al. Investigation on the flow behavior of side channel pumps based on vortex identification[J]. Chinese Journal of Mechanical Engineering, 2021, 34(1): 1-18.
[11] FLEDER A, BÖHLE M. Numerical and experimental investigations on the influence of the blade shape on industrial side channel pumps[C]∥International Rotating Equipment Conference, 2012: 289-298.
[12] LIU C Q, WANG Y Q, YANG Y, et al. New Omega vortex identification method[J]. Science China Physics, Mechanics &Astronomy, 2016, 59(8): 1-9.
[13] LIU C Q, GAO Y S, TIAN S L, et al. Rortex—a new vortex vector definition and vorticity tensor and vector decompositions[J]. Physics of Fluids, 2018, 30(3): 035103.
[14] 杨魏,杨科迪,伏泽,等.不同载荷分布型式下轴流泵叶顶间隙流特性研究[J].农业机械学报,2022,53(6):177-183.YANG Wei,YANG Kedi,FU Ze, et al.Numerical study of blade loading effects on tip leakage flow in axial-flow pump[J].Transactions of the Chinese Society for Agricultural Machinery,2022,53(6):177-183.(in Chinese)
[15] 郭广强,王静宜,张人会,等.液环泵轴向叶顶间隙泄漏流动的等离子体控制数值研究[J].农业机械学报,2022,53(9):160-167.GUO Guangqiang,WANG Jingyi,ZHANG Renhui, et al.Numerical study on plasma control of axial tip clearance leakage flow in liquid ring pump[J].Transactions of the Chinese Society for Agricultural Machinery,2022,53(9):160-167.(in Chinese)
[16] ZHANG N, JIANG J X, GAO B, et al. Numerical analysis of the vortical structure and its unsteady evolution of a centrifugal pump[J]. Renewable Energy, 2020, 155: 748-760.
[17] ZHAO H R, WANG F J, WANG C Y, et al. Study on the characteristics of horn-like vortices in an axial flow pump impeller under off-design conditions[J]. Engineering Applications of Computational Fluid Mechanics, 2021, 15(1): 1613-1628.
[18] 童秉纲,尹协远,朱克勤.涡运动理论[M].合肥:中国科学技术大学出版社,2009.
[19] 吴晓晶.混流式水轮机非定常流动计算和旋涡流动诊断[D].北京:清华大学,2009.
[20] LIU Y, LI X, WANG W, et al. Numerical investigation on the evolution of forces and energy features in thermo-sensitive cavitating flow[J]. European Journal of Mechanics—B/Fluids, 2020, 84: 233-249.
[21] JIN Y X, ZHANG D S, SONG W W, et al. Numerical study on energy conversion characteristics of molten salt pump based on energy transport theory[J]. Energy, 2022, 244: 122674.
[22] HAMMAN C W, KLEWICKI J C, KIRBY R M. On the lamb vector divergence in Navier-Stokes flows[J]. Journal of Fluid Mechanics, 2008, 610: 261-284.
[23] DONG X R, TIAN S L, LIU C Q. Correlation analysis on volume vorticity and vortex in late boundary layer transition[J]. Physics of Fluids, 2018, 30(1):014105.
[24] 陈立为.具有激波和湍流旋涡分离的可压缩绕流数值研究[D].合肥:中国科学技术大学,2010.
[25] QIN Y L, LI D Y, WANG H J, et al. Investigation on the relationship between hydraulic loss and vortex evolution in pump mode of a pump-turbine[J]. Journal of Hydrodynamics, 2022, 34(4): 555-569.