草炭又称泥炭,含有古代埋藏在地下未完全腐烂分解的植物体以及丰富的有机质,是无土栽培主要应用基质[1];选择合适的草炭有利于促进植物根系养分、水分以及空气供应,是培育壮苗、缩短育苗时间的保障[2]。草炭包括砂粒、粉粒、球体、腐殖质-黏粒团聚体及植物纤维残体,其中纤维含量为12.0%~15.0%[3-4]。草炭参数标定,有助于离散元法在草炭覆料研究中的应用,提高育苗基质草炭部分覆料进程的仿真准确性。
离散元法(Discrete element method,DEM)是一种能准确描述物质颗粒流动不连续性质的数值模拟方法[5],能够揭示内在作用机制,缩短研究周期。刘凡一等[6]利用Hertz-Mindlin(no slip)接触模型,以休止角为响应值,标定了小麦间的摩擦因数和小麦-有机板间的静摩擦因数。UCGUL等[7]将线性黏附内聚模型整合到线性Hysteretic Spring模型,获得与实际休止角相近的土壤静摩擦因数、滚动摩擦因数和恢复系数。JIANG等[8]采用API建模方法在EDEM中建立烟条的颗粒模型,以休止角为响应值,标定了烟条间的摩擦因数。丁辛亭等[9]以休止角为响应值,对比响应面和机器学习对显著性参数的优化效果,获取油茶籽的离散元仿真模型接触参数。袁全春等[10]选择Hertz-Mindlin with Johnson-Kendall-Roberts接触模型,以堆积角为响应值,标定有机肥的摩擦因数与表面能JKR。上述研究在标定无黏性、自由流动的颗粒时,通常使用单个响应值(如休止角)作为标定的参考,但单一的休止角响应可能导致多个可行的参数组合,标定结果可靠性差[11],且大多只标定了摩擦因数与恢复系数。其次,以堆积角作为响应值进行的参数标定,离散元仿真模型需要高度的理想化,难以具体且不能考虑颗粒在运动或受外部动力影响时的行为。因此,DEM接触参数的准确标定仍然是再现研究对象实际物理特性的关键因素。
大量随机的草炭湿颗粒随机排列堆积在一起,由于压缩程度的不同,表现出不同程度的弹性、塑性、黏性效应。HORABIK等[12]与ZHAO等[13]基于秸秆的物料特性提出Linear Spring 和Hertz-Mindlin接触模型,但这些模型只能描述变形范围内的弹性行为。XIA等[14]根据煤矿的黏性物料特性,使用Johnson-Kendall-Roberts(JKR)模型标定对休止角敏感的DEM参数,但JKR接触模型不能准确描述物料的塑性特性。LEBLICQ等[15]基于DEMeter++软件提出非线性接触模型表征茎秆之间的塑性特性,但不能表征不同压缩程度的茎秆黏性效应。THAKUR等[16]提出Edinburgh Elasto-Plastic Adhesion (EEPA)接触模型,EEPA 模型在 Hertz 接触理论的基础上,延伸包含了颗粒接触模型的弹塑性和黏性。JANDA等[17]验证了EEPA模型可适用于模拟具有黏性、塑性的土壤粉末。ZHANG等[18]基于EEPA模型标定了秸秆的接触参数,验证了EEPA模型可应用于茎秆类物料,但目前对该模型应用于草炭的参数标定鲜有报道。DING等[19]将草炭视为单一球形土壤模型来建立离散元仿真模型。
本文以草炭为研究对象,以EDEM为离散元仿真工具,选择非线性弹塑性模型(EEPA)作为草炭的接触模型,以草炭单轴密闭压缩的20%、50%轴向应变对应的轴向压力F20、F50为响应值,通过Plackett-Burman Design(PBD)、最陡爬坡和Central Composite Design(CCD)试验对草炭接触模型参数进行标定,旨在获得最优的显著性参数组合。同时,提供一种可行的草炭建模方法来提高参数标定精度。
1.1.1 试验材料及其本征参数
本研究所用草炭产自山东芯喜乐生物科技有限公司。采用基于改进阿基米德原理的排水法测量草炭密度。将质量为M的草炭缓慢放入100 mL量筒内,分别加入30、40、50 mL水,标记水的体积为V1。为了防止加水后草炭向上漂浮,将100 g砝码缓慢放入量筒内,放置于草炭上方测得总体积为V,采用同样的方法测得砝码的体积为VW。草炭密度ρ1计算公式为
(1)
进行6次试验,根据测量结果计算得草炭密度为(0.724±0.085) g/cm3。
采用奥豪斯MB23型水分快速分析仪测量草炭含水率,通过5次试验测得含水率为38.80%~43.40%,满足国标要求[20]。
采用振动筛分法[21]对草炭颗粒度进行分析,振筛机激振力1 kN,振幅小于等于5 mm,使用SFJ-200型不同孔径的标准检验筛随机筛选200 g草炭,得到草炭纤维与草炭颗粒,其中草炭纤维长度15~50 mm,占比16.98%,草炭颗粒粒径分布0~2 mm、2~4 mm、4~6 mm、大于6 mm,分别占比13.560%、42.084%、21.840%、5.536%,其形状主要有球体、类球体、粉末状(图1)。在离散元仿真建模中,颗粒如何建模将很大程度上影响仿真结果的精确性与仿真效率。因此,当涉及大量颗粒作业即生成颗粒数量非常多时,无法建立与实际颗粒结构尺寸完全一样的模型,若采用任意形状的颗粒进行建模仿真,将会成倍地增加计算仿真时间[22-23]。本文设置用类球形代替实际草炭颗粒,草炭纤维用Bonding键联结。通过振动筛分试验得到草炭颗粒尺寸0~6 mm约占90%。草炭颗粒绝大部分是粉末状,参考土壤颗粒泊松比测量方法,采用直剪试验得到草炭内摩擦角为17.76°,根据经验公式
(2)

图1 草炭形状分类图
Fig.1 Charcoal shape particle size classification charts
其中
K0=1-sinθ
(3)
式中 ν1——草炭泊松比
K0——侧压力系数
θ——内摩擦角
通过计算得到试验草炭样品泊松比为0.41[24]。
1.1.2 接触参数测定
(1)草炭-尼龙板间静摩擦因数
参考文献[25],采用斜面法测定草炭-尼龙板间的静摩擦因数,搭建如图2所示的试验平台。选用6组0~2 mm、2~4 mm、4~6 mm草炭颗粒,为了保证草炭颗粒在斜面上滑动而非滚动,每组采用4个质量近似相等的草炭颗粒,在同一平面上将其粘结在一起,将组合颗粒放置于尼龙板上,尼龙板初始角度为0°,缓慢转动旋转轮直至草炭开始有下滑趋势时停止转动,此时倾角仪(深圳维特智能科技有限公司,WT901C-WIFI型)显示值为θ1。每组草炭进行3次试验,共进行18次试验。

图2 静摩擦因数测量
Fig.2 Static friction factor measurement
1.旋转轮 2.机架 3.草炭 4.尼龙板 5.倾角仪
通过μ=tanθ1计算得到草炭-尼龙板间的静摩擦因数μ为0.526±0.051。
(2)草炭-尼龙板间滚动摩擦因数
参考文献[26],采用斜板滚动法与仿真试验相结合的方法来测定草炭-尼龙板间的滚动摩擦因数,搭建图3b所示的滚动摩擦试验平台,选用6组0~2 mm、2~4 mm、4~6 mm草炭,静置于高度为H的倾斜尼龙板上,记录此时的倾角仪数值,使草炭颗粒自由滚动至停止,水平滚动距离为S,每组草炭进行3次试验,共进行18次试验。
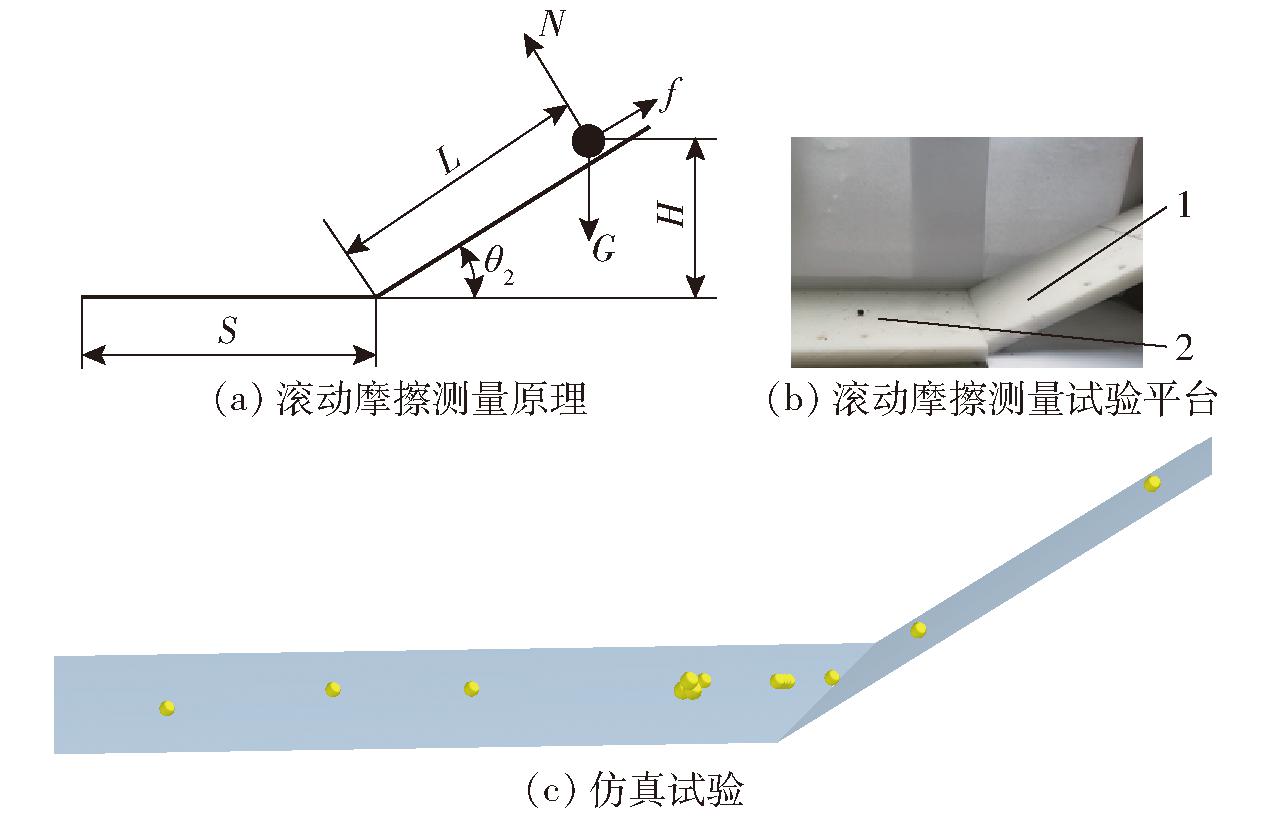
图3 滚动摩擦因数测量
Fig.3 Rolling friction factor measurement
1.尼龙板 2.草炭
由于草炭颗粒多为非规则形体,当倾角θ2与斜面滚动距离L较大时,会导致草炭颗粒在滚动过程中发生弹跳,影响试验结果准确性,当倾角θ2与L较小时,草炭颗粒滚动距离较小,不利于试验测量,因此经大量预试验调整,设定倾角为30°,斜面滚动距离L为185 mm。假设草炭在纯滚动过程中只受到滚动摩擦力影响,则通过能量守恒定律可得
GH=μfG(Lcosθ2+S)
(4)
式中 μf——草炭-尼龙板间滚动摩擦因数
G——草炭重力,N
仿真试验以滚动摩擦因数为因素,水平滚动距离S为指标进行单因素仿真试验(图3c),在EDEM中设置已标定的静摩擦因数、参考碰撞恢复系数[20],其余接触参数设为0,滚动摩擦因数设置为0.2~0.4,水平间隔为0.1,将试验结果导入Origin绘制成散点图,并拟合曲线(图4)。拟合方程为
(5)
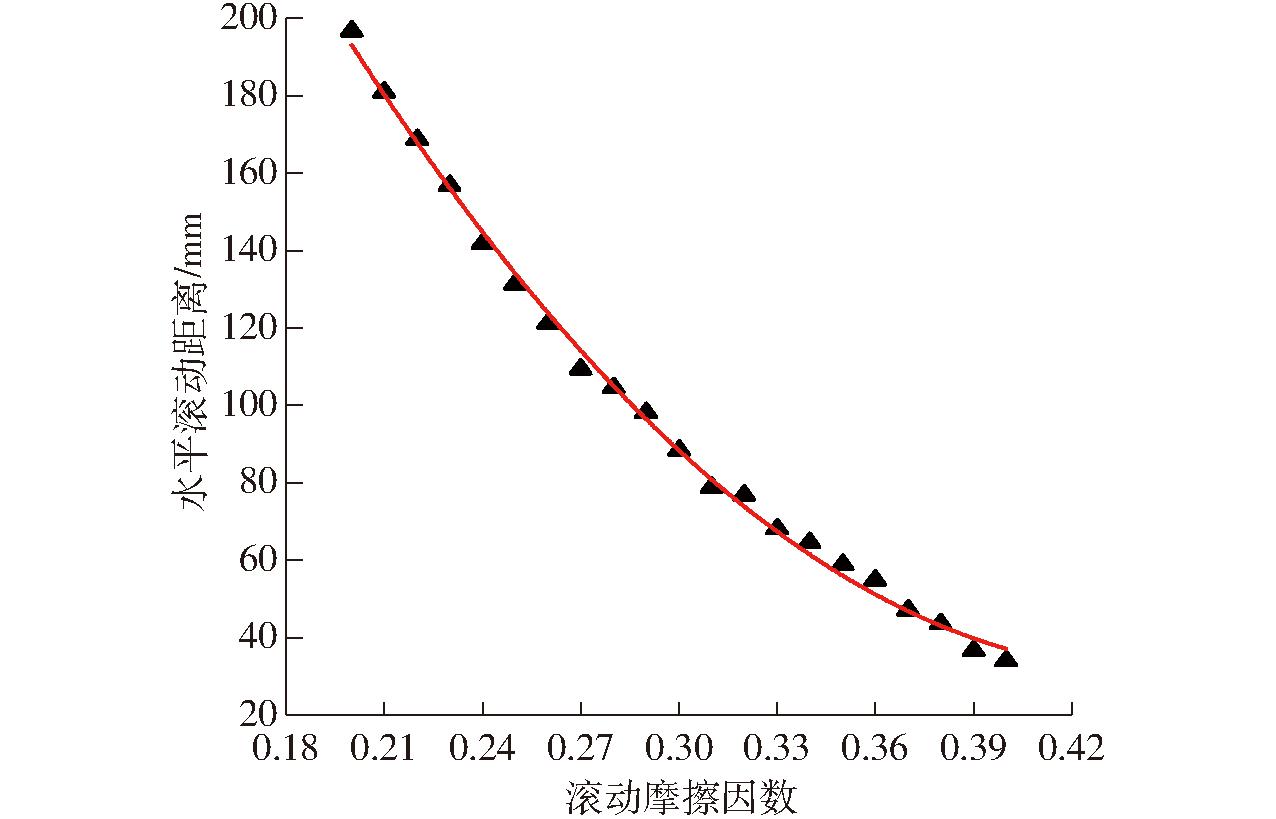
图4 滚动摩擦因数与水平滚动距离拟合曲线
Fig.4 Fitting curves of rolling friction coefficient and horizontal rolling distance
将实际测试的水平滚动距离代入式(5),计算得到草炭-尼龙板间的滚动摩擦因数μf为0.272±0.012,将其代入EDEM进行验证,得到仿真水平滚动距离为108.443 mm,与实际水平滚动距离均值111.583 mm相对误差为2.896%,小于5%,误差较小。
草炭轴向压力随时间变化的曲线通过单轴密闭压缩试验来获得[27]。用于单轴密闭压缩试验的圆筒,由两个半径46 mm、高度60 mm的尼龙材质半圆筒通过螺母螺栓连接而成。如图5所示,将25 g草炭自然注入到圆筒中,使用DDL10型万能试验机(长春机械科学研究所有限公司,负载精度±5%)以恒定速率8 mm/s推动压板向下加载,压板直径46 mm,最大载荷10 kN。当加载至固结应力100 kPa和300 kPa时,以恒定速率4 mm/s上升,直至完全卸载。

图5 单轴密闭压缩试验
Fig.5 Uniaxial confined compression test
1.万能试验机 2.压板 3.圆筒 4.支撑板
如图6所示,单轴密闭压缩试验分别加载固结应力至100、300 kPa。草炭轴向压力位移曲线可分为低刚度阶段、准线性阶段、曲线阶段。由于预应变的存在,压缩试验曲线在轴向应变20%左右由准线性阶段向曲线阶段过渡,100、300 kPa试验曲线在轴向应变50%左右时开始出现较大差异,将F20、F50表示为草炭压缩轴向应变20%、50%时的轴向压力。本文仅将F20、F50作为草炭离散元参数标定的响应值。
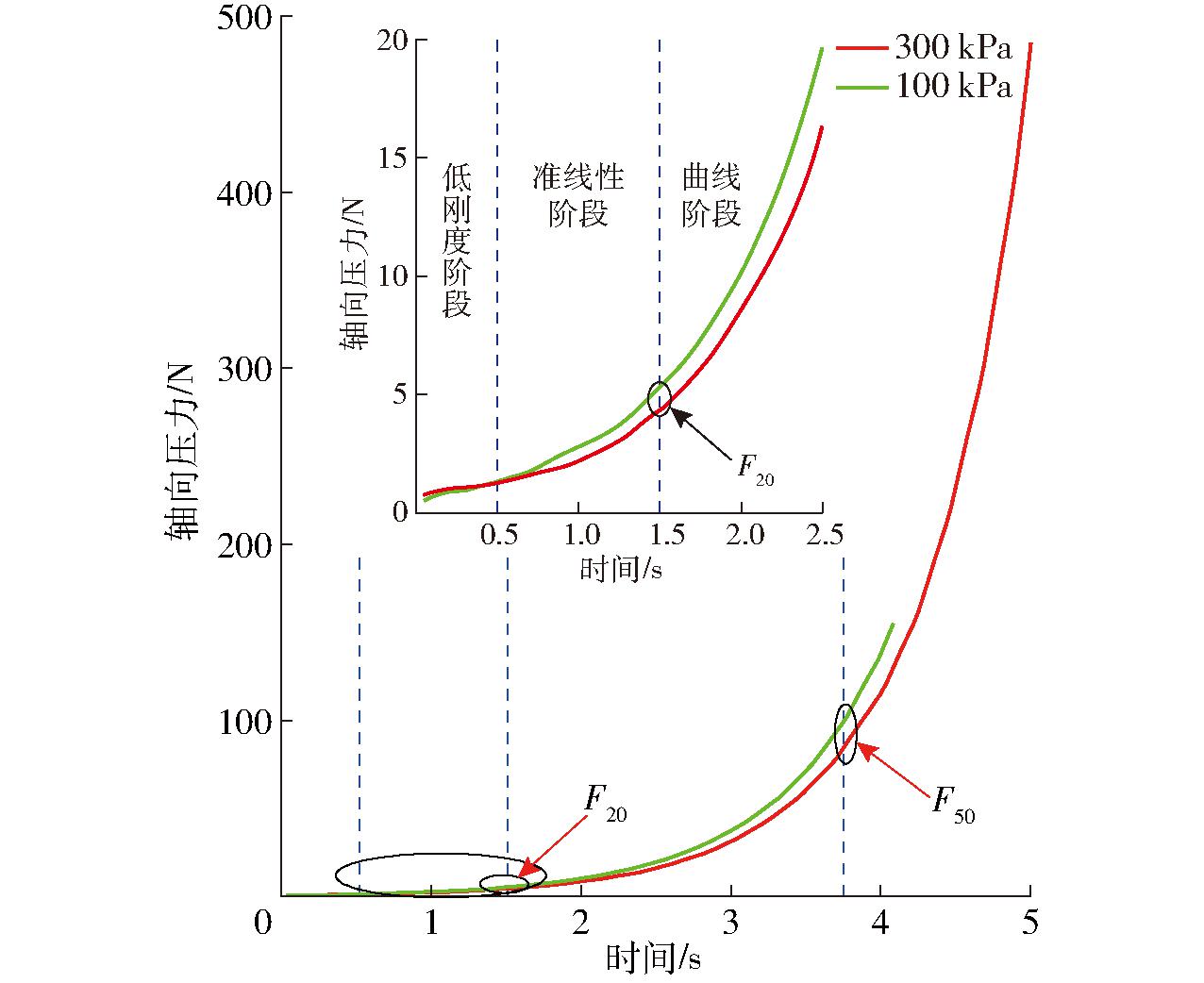
图6 单轴密闭压缩试验曲线
Fig.6 Uniaxial confined compression test curves
根据草炭单轴密闭压缩试验曲线得到草炭属于非线性弹塑性介质,不同程度的单轴压缩对弹塑性材料的强度有很大影响,物料孔隙度因固结应力水平的不同而不同,接触模型的选择应能够捕捉物料强度随固结应力水平的变化[17,28]。
EEPA接触模型用非线性滞后弹簧模型表征弹塑性接触变形,以及作为塑性接触变形函数的粘着力部分[29]。该接触模型能较好地模拟草炭在压缩过程中的弹塑性行为;因此,选择EEPA接触模型作为草炭与草炭之间的接触模型。EPPA颗粒间接触模型在 EDEM 软件应用过程中主要参数包括恢复系数、静摩擦因数、滚动摩擦因数、恒定初始黏结强度、表面能、接触塑性变形比、加载分支指数、黏结分支指数和切向刚度因子。恒定初始黏结强度恒定存在于颗粒之间,对试验过程影响较小,将恒定初始黏结强度因素不予考虑,大小定义为0[30];加载分支指数取为1或1.5,区别于加载分支指数取为1 时与Hysteretic Spring模型加载卸载过程中应力-应变曲线特征相似,本研究加载分支指数取1.5[31]。
1.3.1 草炭离散元建模
约90%草炭颗粒尺寸介于0~6 mm,且绝大部分是不规则形状;如图7所示,本文将草炭离散元建模按实际试验筛分为草炭颗粒与草炭纤维两部分,草炭颗粒按实际尺寸分为0~2 mm、 2~4 mm、 4~6 mm,将大于6 mm的颗粒部分归入为4~6 mm。各尺寸范围内颗粒随机生成,随机生成颗粒尺寸按实际颗粒形状尺寸设置最大、最小值,其中草炭纤维长度在15~50 mm。考虑到草炭纤维建模的准确性,本文设置草炭纤维基准尺寸32.3 mm,由9个长度3.5 mm的类球形单元体连接而成,类球形单元体宽2 mm,采用Bonding V2模型连接单元体,随机在基准尺寸0.5~1.5倍范围内生成草炭纤维。Bonding V2模型能够准确描述草炭的弯曲、扭转和剪切力学性能[18],其黏结参数[32]如表1所示。
表1 Bonding V2模型参数
Tab.1 Bonding V2 model parameters

参数数值单位面积法向刚度/(N·m-3)4.1551×109单位面积剪切刚度/(N·m-3)8.0749×108法向强度/MPa10剪切强度/MPa1.3粘结圆盘尺度1.0
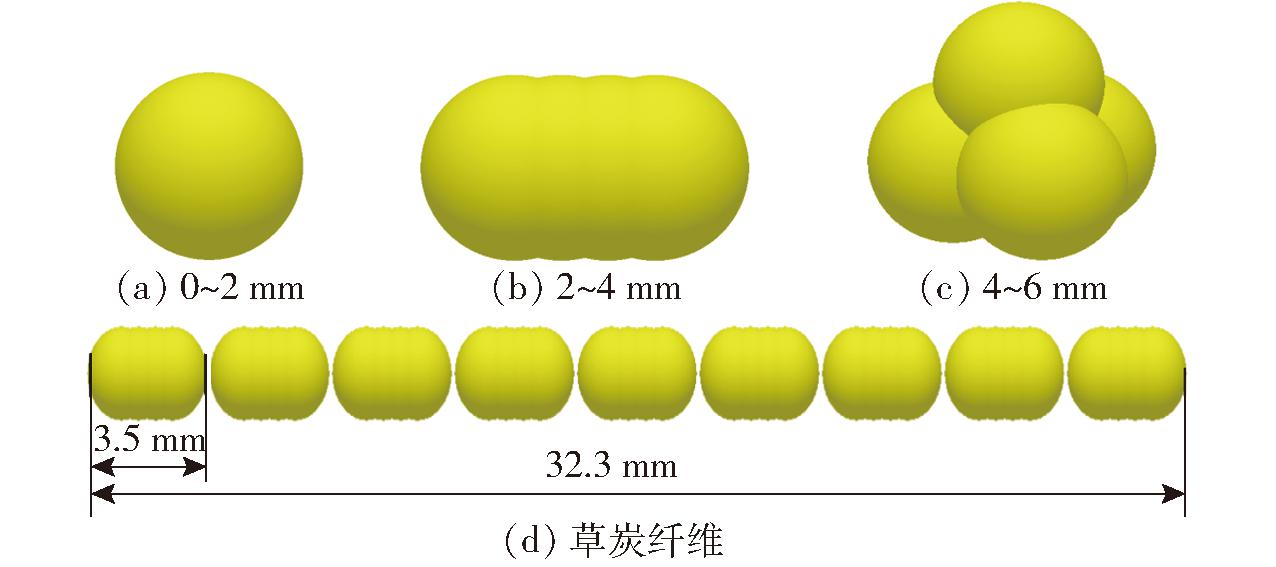
图7 草炭颗粒模型
Fig.7 Modeling of substrate charcoal pellets
1.3.2 压缩草炭仿真
压缩草炭离散元仿真颗粒与接触部件模型选择Hertz-Mindlin(no slip),建立与实际试验一样尺寸的圆筒生成草炭颗粒,草炭密度、草炭-尼龙板间静摩擦因数、草炭-尼龙板间滚动摩擦因数取其实测平均值,仿真参数设置如表2所示。
表2 压缩仿真参数
Tab.2 Compression simulation parameters

参数数值草炭密度ρ1/(g·cm-3)0.724尼龙板密度ρ2/(g·cm-3)1.140草炭尼龙板间静摩擦因数0.526草炭尼龙板间滚动摩擦因数0.272草炭泊松比ν10.410尼龙板泊松比ν20.280草炭尼龙板间碰撞恢复系数0.120尼龙板剪切模量/MPa3200
所有颗粒生成在半径23 mm、高度60 mm的圆筒内,草炭质量与实际试验保持一致,设定生成25 g草炭,包括0~6 mm草炭颗粒21 g、草炭纤维4 g。生成颗粒时间设置1.8 s,生成颗粒朝竖直方向叠加堆积在一起(图8a)。颗粒生成以后,在圆筒顶部建立半径23 mm、厚度4 mm的压缩圆板。圆板以恒速8.00 mm/s向下压缩,压缩至轴向应变60%时停止压缩(图8b)。
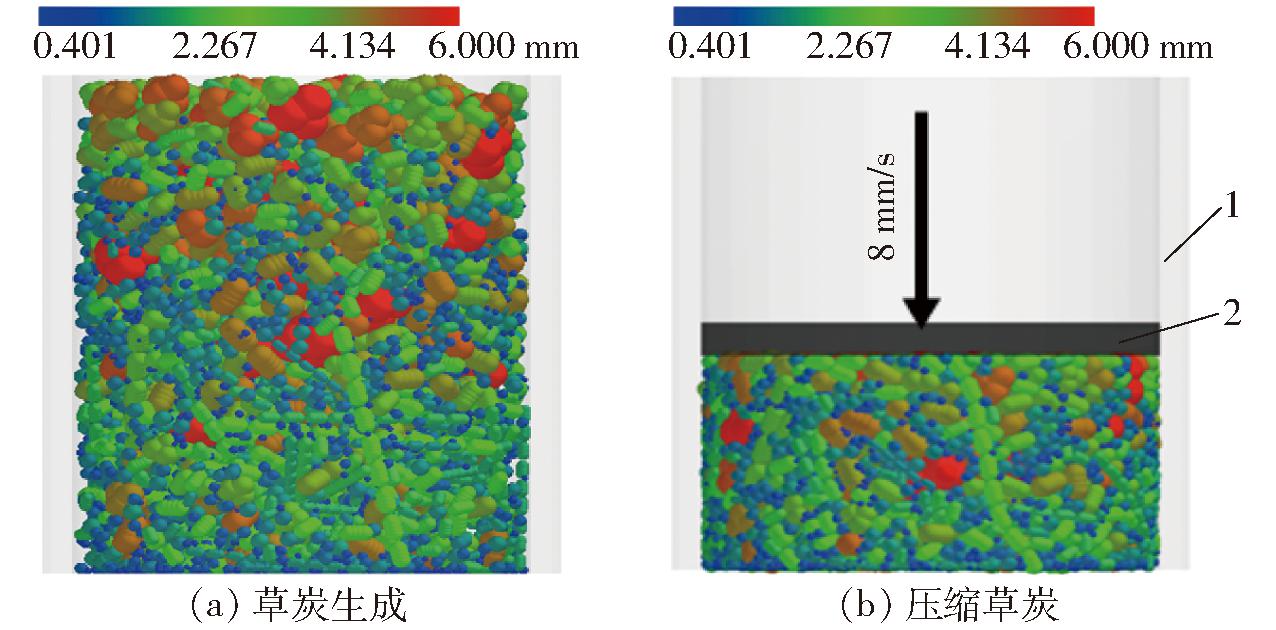
图8 压缩草炭仿真
Fig.8 Compressed substrate charcoal simulation
1.圆筒 2.压板
1.4.1 Plackett-Burman Design试验筛选显著性参数
本文应用Design-Expert 13软件进行PBD试验设计与分析,以压缩草炭的20%、50%轴向应变对应的轴向压力作为响应值。对草炭的接触参数(草炭间恢复系数、草炭间静摩擦因数、草炭间滚动摩擦因数、草炭-尼龙板间恢复系数)、草炭剪切模量和EEPA接触模型参数(表面能、塑性变形比、黏结分支指数、切向刚度因子)进行筛选,筛选出对压缩草炭试验曲线有显著影响的参数。
将仿真规模、草炭堆积密度和堆积角等输入EDEM颗粒材料数据库(Generic EDEM material model database,GEMM)获取各参数的大致取值范围。如图9所示,在实际堆积角试验中,草炭堆积近似为均匀分布圆锥体(图9a),使用Matlab采用图像处理方法测得草炭堆积角,首先去除冗余背景(图9b),对图像进行灰度变化(图9c)与二值化处理(图9d)以便采用柯西算子进行边界轮廓提取(图9e)。最后对边界轮廓图像以堆积最高点为中点进行左右分割[26],形成左右两个单边图像(图9f、9g),提取单边图像轮廓坐标(图9h),采用最小二乘法对边界轮廓的斜率进行线性拟合(图9i),并且将堆积角切线与水平线之间的角度定义为堆积角,计算得到堆积角θ3=arctan|k|,k为拟合直线斜率,取两侧的平均值作为草炭的堆积角[33]。草炭堆积密度1~1.5 g/cm3,堆积角40°~45°,结合软件内置GEMM颗粒材料数据库与文献[34-37]参数取值范围,取草炭间恢复系数0.2~0.8,草炭间静摩擦因数0.2~1.0,草炭间滚动摩擦因数0.05~0.3,表面能4~16 J/m2。根据文献[29,36],可知塑性变形比为0.2~0.6,黏结分支指数为0.5~3,切向刚度因子为0.3~0.9。
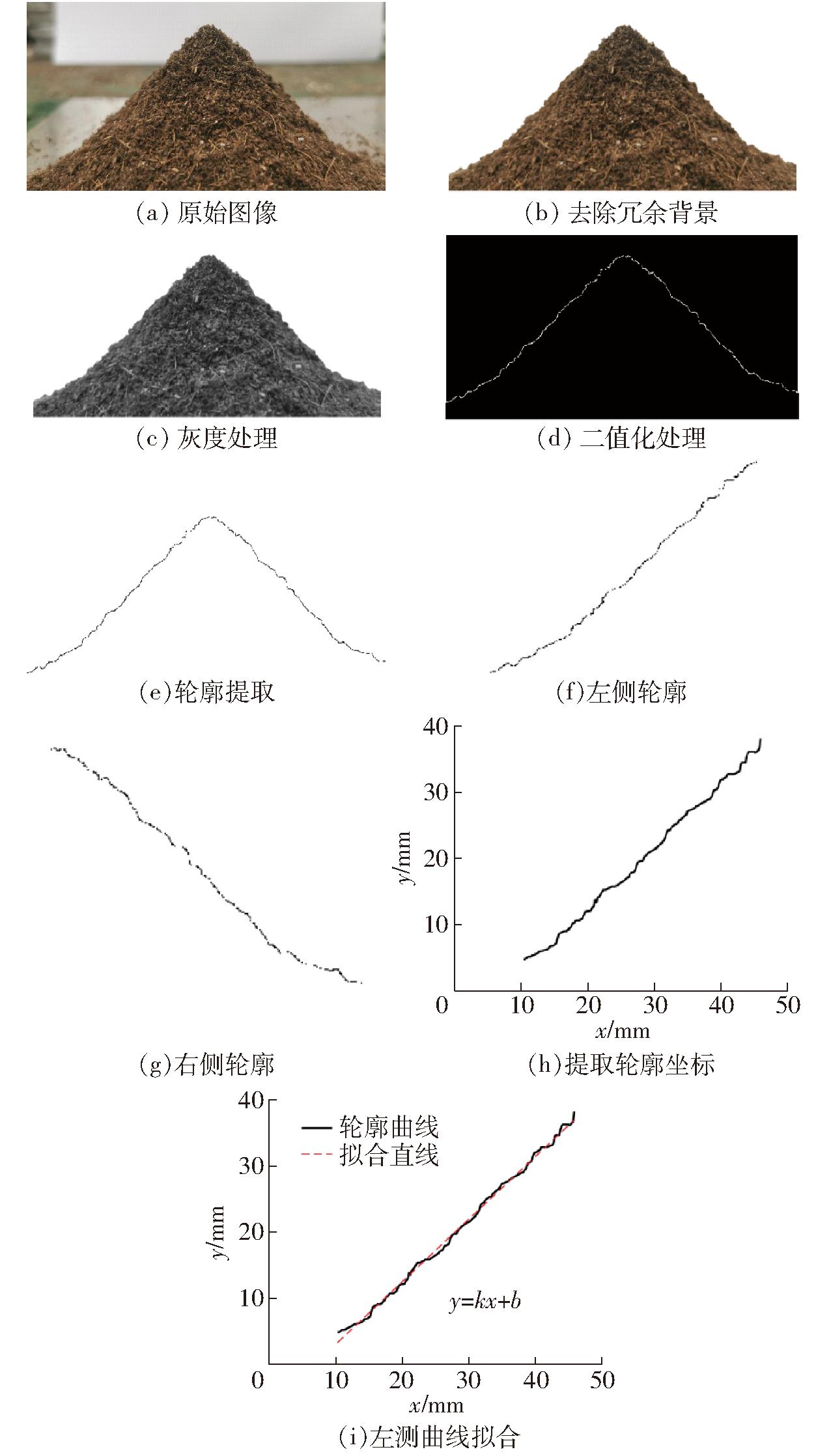
图9 图像处理测量堆积角
Fig.9 Image processing to measure stacking angle
PBD试验各参数分别用A~J表示,共8个参数。通过试验与参考相关文献,得到参数取值如表3所示。
表3 PBD因素编码
Tab.3 Factors and codes of PBD
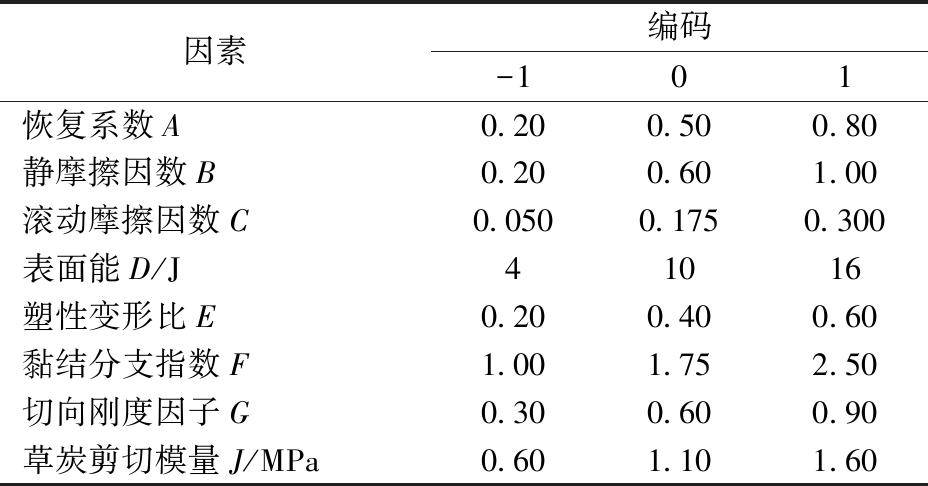
因素编码-101恢复系数A0.200.500.80静摩擦因数B0.200.601.00滚动摩擦因数C0.0500.1750.300表面能D/J41016塑性变形比E0.200.400.60黏结分支指数F1.001.752.50切向刚度因子G0.300.600.90草炭剪切模量J/MPa0.601.101.60
1.4.2 最陡爬坡试验
最陡爬坡试验是针对显著性参数设计的,可以较快地缩小最优值参数所在的区间。根据PBD的试验结果, 本文只将4个显著性参数(草炭间恢复系数、草炭间静摩擦因数、切向刚度因子、草炭剪切模量)进行最陡爬坡试验。根据方差分析确定爬坡方向,按照选定步长逐步变化,将非显著性参数取PBD参数的中间水平,将轴向压力的仿真值与实际值的相对误差作为最陡爬坡试验的试验指标,观察试验与仿真结果的误差变化,直到该误差达到最小值后又逐步增大,试验方案与结果如表4所示。
表4 最陡爬坡试验方案与结果
Tab.4 Scheme and result of the steepest ascent test
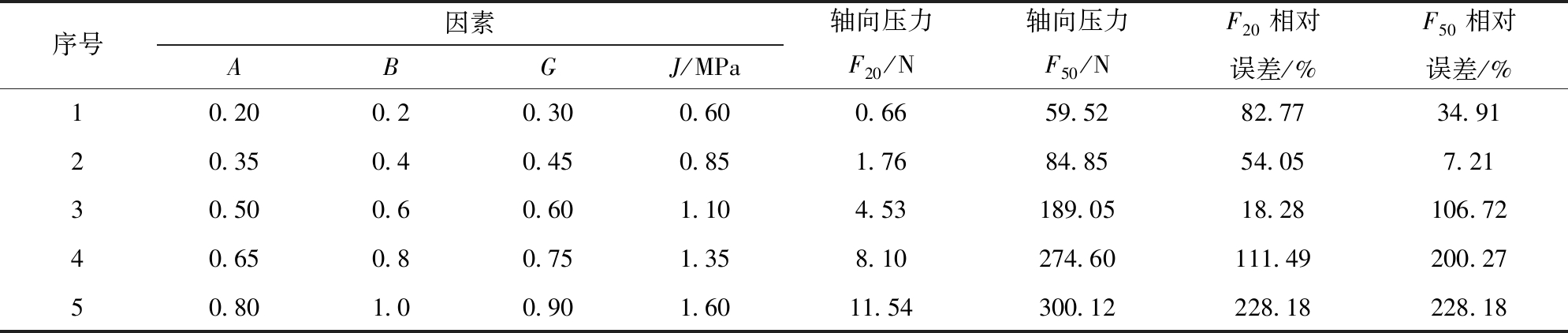
序号因素ABGJ/MPa轴向压力F20/N轴向压力F50/NF20相对误差/%F50相对误差/%10.200.20.300.600.6659.5282.7734.9120.350.40.450.851.7684.8554.057.2130.500.60.601.104.53189.0518.28106.7240.650.80.751.358.10274.60111.49200.2750.801.00.901.6011.54300.12228.18228.18
1.4.3 中心组合响应面试验
基于最陡爬坡试验确定离散元参数最佳范围,采用中心组合响应面(Central composite design, CCD)进行响应面分析试验,确定最优参数,建立轴向压力与显著性参数的关系模型。在试验中,非显著性参数取PBD试验的中间值,显著性参数及仿真因素编码如表5所示。
表5 CCD因素编码
Tab.5 Factors and codes of CCD
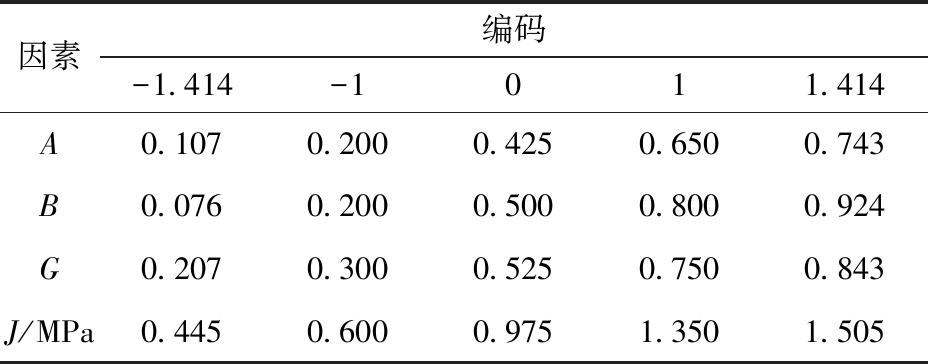
因素编码-1.414-1011.414A0.1070.2000.4250.6500.743B0.0760.2000.5000.8000.924G0.2070.3000.5250.7500.843J/MPa0.4450.6000.9751.3501.505
PBD试验设计方案及结果如表6所示,A′~J′为A~J的编码值。使用Design-Expert软件进行方差分析,得到8个参数对响应值的影响效果和可信度分析。如表7所示,草炭间静摩擦因数对响应值F20影响极显著(P<0.01),草炭剪切模量对响应值F20影响显著(P<0.05),草炭间静摩擦因数、草炭剪切模量对响应值F50影响极显著(P<0.01),草炭间恢复系数、切向刚度因子对响应值F50影响显著(P<0.05)。F20响应值指标校正系数![]() 为0.918 4,精密度为12.233 5;F50响应值指标校正系数
为0.918 4,精密度为12.233 5;F50响应值指标校正系数![]() 为0.933 5,精密度13.741 8;校正系数要求大于0.8,精密度要求大于4,本次试验具有可靠性,且F50响应值对应的参数影响可靠性更高。因此,本文将草炭间恢复系数、草炭间静摩擦因数、切向刚度因子、草炭剪切模量设定为显著性参数,最陡爬坡试验与CCD试验时只考虑这4个因素。
为0.933 5,精密度13.741 8;校正系数要求大于0.8,精密度要求大于4,本次试验具有可靠性,且F50响应值对应的参数影响可靠性更高。因此,本文将草炭间恢复系数、草炭间静摩擦因数、切向刚度因子、草炭剪切模量设定为显著性参数,最陡爬坡试验与CCD试验时只考虑这4个因素。
表6 PBD方案及结果
Tab.6 Scheme and results of PBD
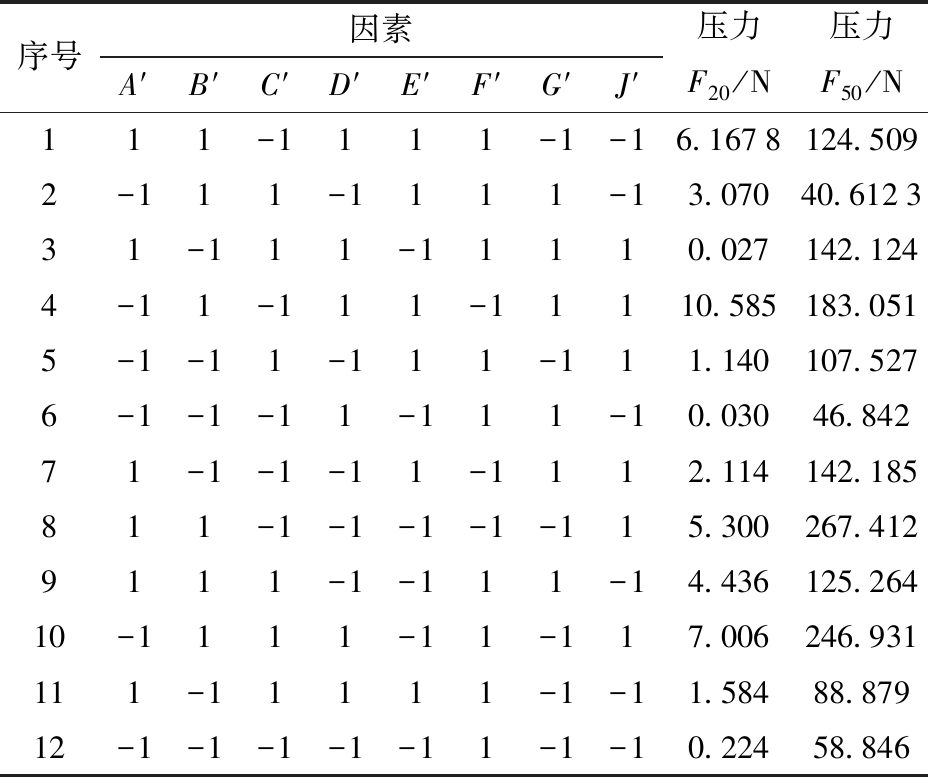
序号因素A′B′C′D′E′F′G′J′压力F20/N压力F50/N111-1111-1-16.1678124.5092-111-1111-13.07040.612331-111-11110.027142.1244-11-111-11110.585183.0515-1-11-111-111.140107.5276-1-1-11-111-10.03046.84271-1-1-11-1112.114142.185811-1-1-1-1-115.300267.4129111-1-111-14.436125.26410-1111-11-117.006246.931111-11111-1-11.58488.87912-1-1-1-1-11-1-10.22458.846
表7 PBD试验方差分析
Tab.7 ANOVA of test of PBD
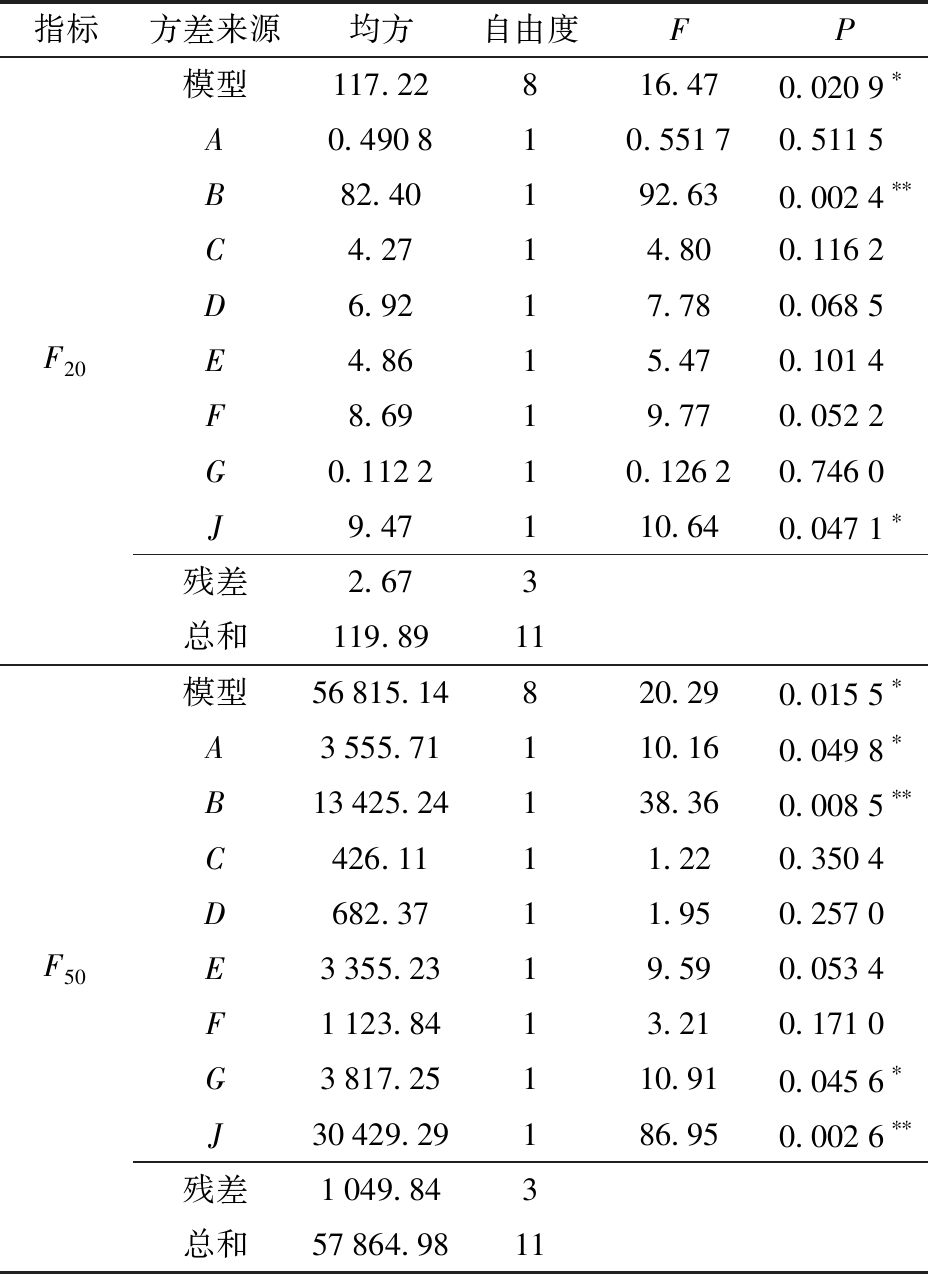
注:*表示影响显著(0.01≤P<0.05),**表示影响极显著(P<0.01)。下同。
指标方差来源均方自由度FP模型117.22816.470.0209∗A0.490810.55170.5115B82.40192.630.0024∗∗C4.2714.800.1162D6.9217.780.0685F20E4.8615.470.1014F8.6919.770.0522G0.112210.12620.7460J9.47110.640.0471∗残差2.673总和119.8911模型56815.14820.290.0155∗A3555.71110.160.0498∗B13425.24138.360.0085∗∗C426.1111.220.3504D682.3711.950.2570F50E3355.2319.590.0534F1123.8413.210.1710G3817.25110.910.0456∗J30429.29186.950.0026∗∗残差1049.843总和57864.9811
根据PBD试验结果,显著性参数与响应值之间呈正向相关,即随着显著性参数的增大,轴向压力增大。与此相反,轴向压力相对误差先减小后增大。第2组和第3组相对误差最小,因此,选择1~4组,即各显著性参数的最佳范围为:草炭间恢复系数0.2~0.65、草炭间静摩擦因数0.2~0.8、切向刚度因子0.3~0.75、草炭剪切模量0.60~1.35 MPa。
基于PBD试验与最陡爬坡试验分析,应用CCD设计试验进行响应面分析并寻求最优解,以A′、B′、G′、J′为试验因素编码,以F20、F50为响应值指标。共进行30组试验,设计方案与结果如表8所示。
表8 CCD试验方案与结果
Tab.8 Scheme and results of CCD
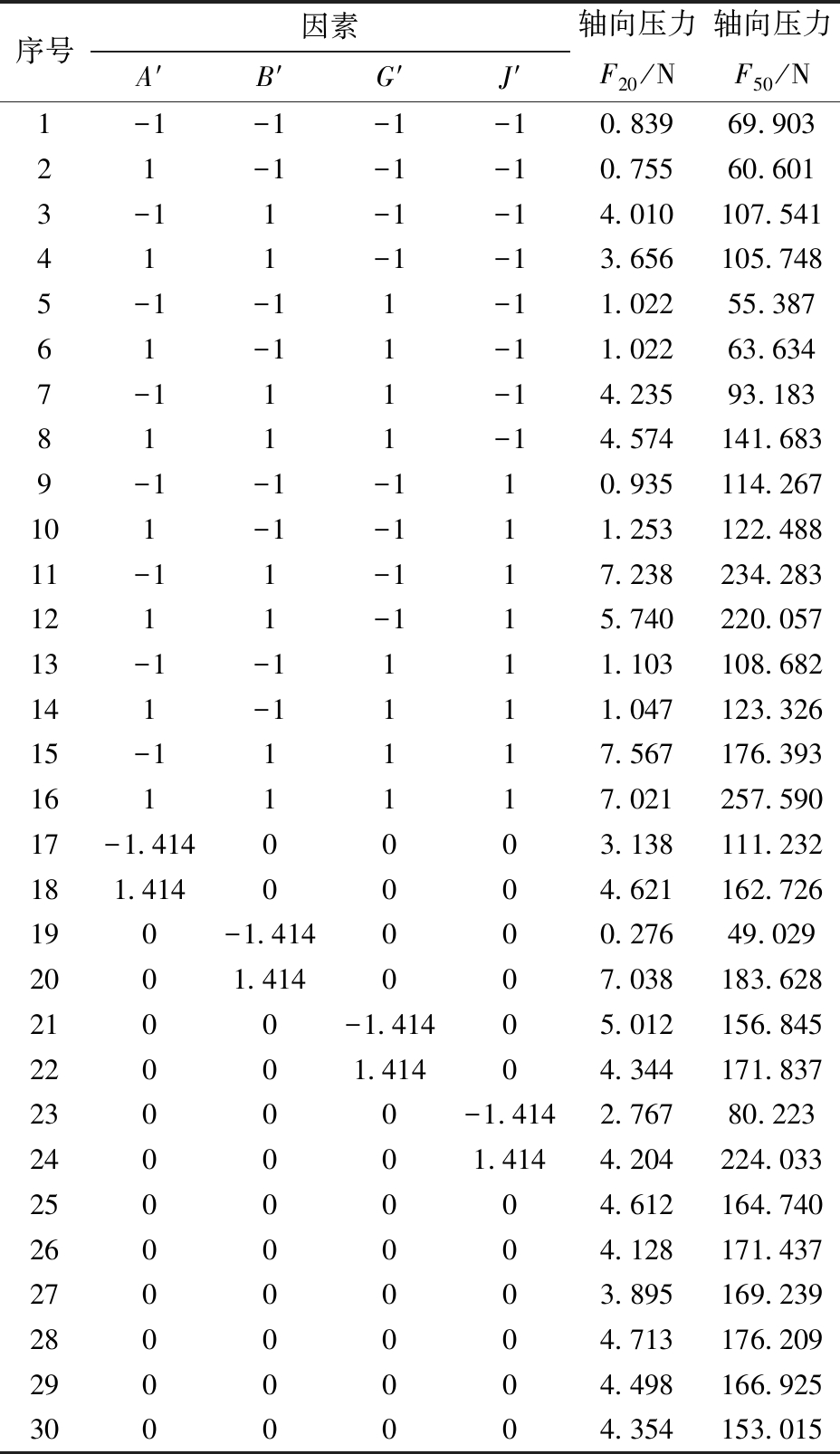
序号因素A′B′G′J′轴向压力F20/N轴向压力F50/N1-1-1-1-10.83969.90321-1-1-10.75560.6013-11-1-14.010107.541411-1-13.656105.7485-1-11-11.02255.38761-11-11.02263.6347-111-14.23593.1838111-14.574141.6839-1-1-110.935114.267101-1-111.253122.48811-11-117.238234.2831211-115.740220.05713-1-1111.103108.682141-1111.047123.32615-11117.567176.3931611117.021257.59017-1.4140003.138111.232181.4140004.621162.726190-1.414000.27649.0292001.414007.038183.6282100-1.41405.012156.84522001.41404.344171.83723000-1.4142.76780.223240001.4144.204224.0332500004.612164.7402600004.128171.4372700003.895169.2392800004.713176.2092900004.498166.9253000004.354153.015
应用Design-Expert软件对试验结果进行分析,建立响应值与离散元参数之间的回归关系。对回归模型进行方差分析,如表9所示,草炭间恢复系数(A)对响应值F50影响极显著,草炭间静摩擦因数(B)、草炭剪切模量(J)对响应值F20、F50影响极显著。草炭间静摩擦因数(B)和草炭剪切模量(J)之间的交互作用(BJ)对响应值F20、F50影响极显著;草炭间恢复系数(A)和切向刚度因子(G)之间的交互作用(AG)对响应值F50影响极显著。草炭间恢复系数平方项(A2)对响应值F50有显著影响,草炭间静摩擦因数平方项(B2)对响应值F20有显著影响,对响应值F50影响极显著。另外,草炭剪切模量平方项(J2)对响应值F20有极显著影响。
表9 CCD二次回归模型方差分析
Tab.9 ANOVA of central CCD model
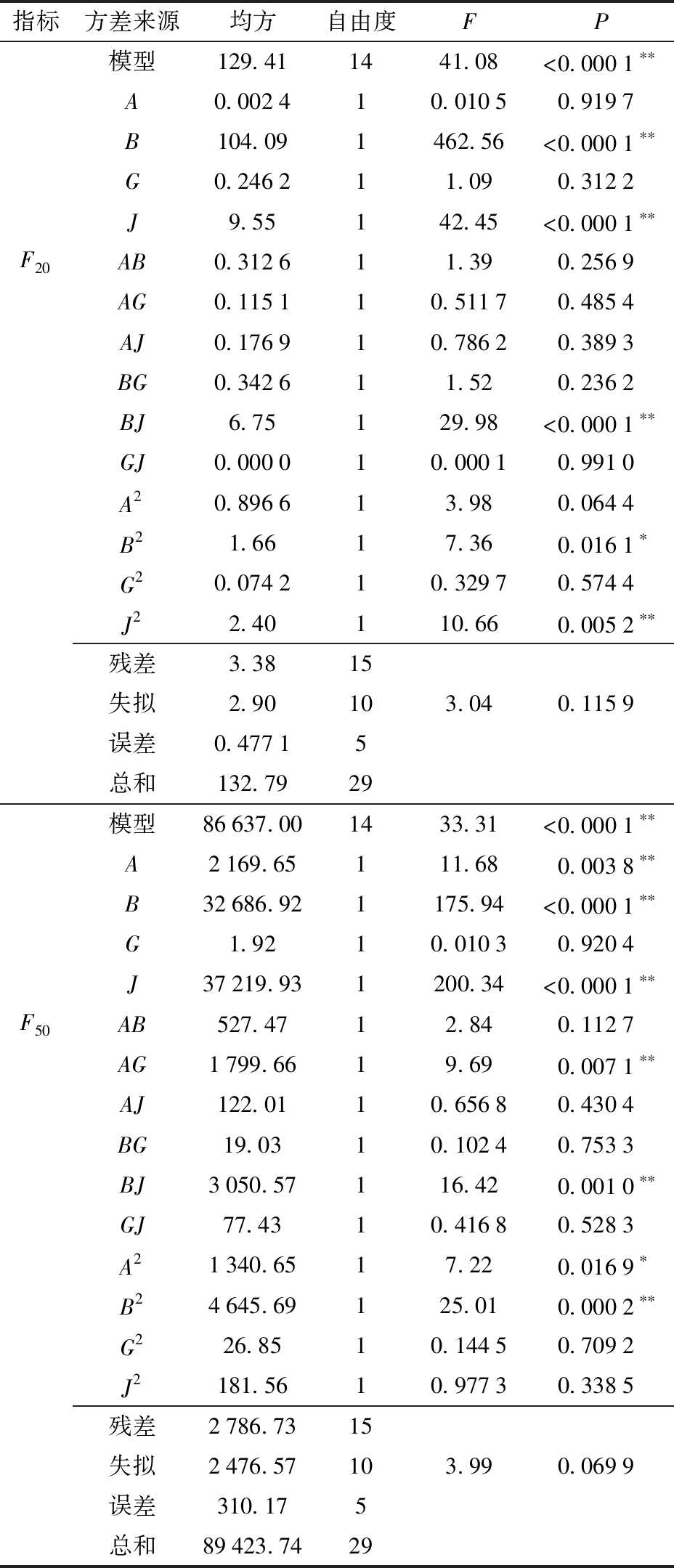
指标方差来源均方自由度FP模型129.411441.08<0.0001∗∗A0.002410.01050.9197B104.091462.56<0.0001∗∗G0.246211.090.3122J9.55142.45<0.0001∗∗F20AB0.312611.390.2569AG0.115110.51170.4854AJ0.176910.78620.3893BG0.342611.520.2362BJ6.75129.98<0.0001∗∗GJ0.000010.00010.9910A20.896613.980.0644B21.6617.360.0161∗G20.074210.32970.5744J22.40110.660.0052∗∗残差3.3815失拟2.90103.040.1159误差0.47715总和132.7929模型86637.001433.31<0.0001∗∗A2169.65111.680.0038∗∗B32686.921175.94<0.0001∗∗G1.9210.01030.9204J37219.931200.34<0.0001∗∗F50AB527.4712.840.1127AG1799.6619.690.0071∗∗AJ122.0110.65680.4304BG19.0310.10240.7533BJ3050.57116.420.0010∗∗GJ77.4310.41680.5283A21340.6517.220.0169∗B24645.69125.010.0002∗∗G226.8510.14450.7092J2181.5610.97730.3385残差2786.7315失拟2476.57103.990.0699误差310.175总和89423.7429
F20、F50对应回归模型P<0.000 1,说明响应值与所得回归方程的关系是极显著的;失拟项P=0.115 9>0.05、P=0.069 9>0.05,说明所得回归方程与实际拟合中非正常误差比例小,拟合性较好,决定系数R2=0.974 6、R2=0.968 8。剔除对回归模型影响不显著的因素,进行二次回归模型方差分析。精确度由20.709 6变为31.640 3、由21.473 0变为28.681 8,失拟项由0.115 9变为0.132 1、由0.069 9变为0.088 9,精确性和可靠性得到改善,优化后获得轴向压力回归方程为
F50=-38.088+146.653A+269.013B-87.659G+53.669J+209.494AG+122.738BJ-247.466A2-253.925B2
(6)
F20=-3.472+0.048A+7.147B+0.493G+6.599J+5.772BJ-5.169B2-3.919J2
(7)
取草炭间恢复系数(A)与切向刚度因子(G)为中间值,草炭间静摩擦因数(B)与草炭剪切模量(J)的响应曲面如图10所示,当取相同的响应值时,随着草炭剪切模量(J)的减小,草炭间静摩擦因数(B)增大,且草炭间静摩擦因数(B)相邻区域差值的变化逐渐增大,曲线斜率增大,F50响应值对应的曲线斜率变化比F20响应值对应的曲线斜率变化更加明显;当草炭剪切模量(J)不变时,随着草炭间静摩擦因数(B)的增大,响应值轴向压力也逐渐增大。草炭间静摩擦因数(B)与草炭剪切模量(J)的变化与响应值呈正向相关性,且随着草炭间静摩擦因数(B)与草炭剪切模量(J)的增大,响应值越来越显著,即响应面越来越陡峭。

图10 交互因素对轴向压力的影响
Fig.10 Effect of interactive factors on axial pressure
在轴向压力F20、F50上下限10%范围内进行参数优化,借助Design-Expert 13的Numerical模块对显著性参数进行寻优,以Desirability值为参考,设定约束寻优条件

(8)
对得到的若干组解取6组进行单轴密闭压缩仿真验证,选择与实际试验平均误差最小的一组为最优解。优化后最优解为:草炭间恢复系数0.202、草炭间静摩擦因数0.595、切向刚度因子0.667、草炭剪切模量0.613 MPa。
根据响应面参数标定结果,验证其最优参数组合的可靠性,利用EDEM软件建立草炭离散元模型,进行单轴密闭压缩仿真试验,考察离散元模型和参数的通用性。如图11所示,使用Origin软件将1.50~3.75 s(轴向应变20%~50%)范围内的仿真结果轴向压力曲线与实测的轴向压力变化曲线进行对比分析,取其范围内轴向压力的平均值,得到实测轴向压力平均值为28.96 N,仿真轴向压力平均值为31.65 N,相差2.69 N,实测值与仿真值平均误差约为8.08%。相对误差在轴向应变40%左右达到最大值,为15.34%。因此,该研究建立的离散元仿真模型和参数标定可以准确描述草炭的压缩特性。
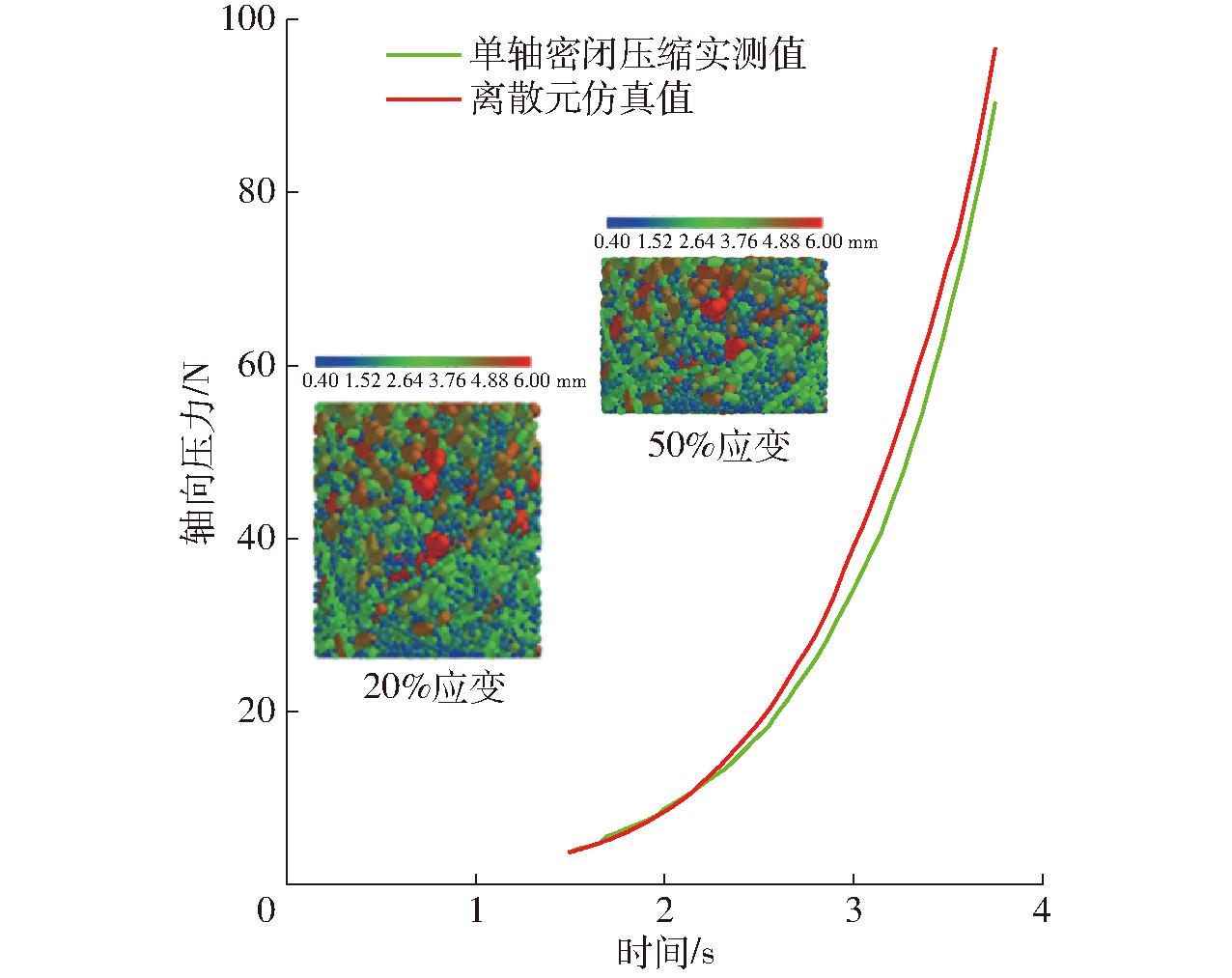
图11 仿真与实测曲线
Fig.11 Comparison of simulation and measured curves
对草炭的单轴密闭压缩前期主要是对颗粒与颗粒之间空隙的压缩,这一过程将会导致较大塑性变形比的发生。草炭间的塑性变形比对响应值影响也较大,因而在此次试验中造成实测值与仿真值相对误差较大。
(1)基于离散元EDEM软件,选取EEPA接触模型并对草炭进行离散元建模及单轴密闭压缩仿真;通过PBD试验和最陡爬坡试验筛选出对轴向压力影响显著的参数,分别是草炭间恢复系数、草炭间静摩擦因数、切向刚度因子、草炭剪切模量,并缩小区间。
(2)根据CCD试验,进行响应面二次回归分析,得到草炭间静摩擦因数显著性最大,随着压缩的进行,草炭间恢复系数的影响效果上升。构建显著性参数与响应值间的二次回归模型,以轴向应变20%、50%对应的轴向压力3.83、91.45 N为目标值对显著性参数进行寻优,得到显著性参数最优组合如下:草炭间恢复系数为0.202、草炭间静摩擦因数为0.595、切向刚度因子为0.667、草炭剪切模量为0.613 MPa。
(3)通过将最优参数组合的仿真试验与单轴密闭压缩物理试验进行对比,发现在轴向应变范围20%~50%内,随着压缩应变的增加,物理压缩的变化程度逐渐小于仿真压缩,仿真压缩曲线呈现出较陡的斜率。轴向压力仿真平均值与实测平均值相差2.69 N,仿真值与实测值平均相对误差为8.08%。
[1] 胡蒙爱, 马嘉伟, 张雪艳. 生物炭引入蚯蚓粪和草炭对基质环境、黄瓜植株生长和果实品质特性的影响[J]. 江西农业大学学报, 2022, 44(4): 852-861. HU Mengai, MA Jiawei, ZHANG Xueyan. Effects of introducing biochar into vermicompost and peat on substrate environment, cucumber growth and quality characteristics[J]. Acta Agriculturae Universitatis Jiangxiensis, 2022, 44(4): 852-861. (in Chinese)
[2] 刘景霞. 不同温度、光照和基质对辣椒幼苗生长的影响[D].长沙: 湖南农业大学, 2010.LIU Jingxia. The effect of different light and temperature conditions and substrates on the growth of pepper seedlings[D]. Changsha: Hunan Agricultural University, 2010. (in Chinese)
[3] BADV K, SAYADIAN T. An investigation into the geotechnical characteristics of Urmia peat[J]. Transactions of Civil Engineering, 2012, 36(C2): 167-180.
[4] 胡天明. 敦化市江源镇草炭土剪切特性及本构模型研究[D]. 长春: 吉林大学, 2020.HU Tianming. Study on the shear characteristics and constitutive model of turfy soil in Jiangyuan Town, Dunhua City[D]. Changchun: Jilin University, 2020. (in Chinese)
[5] CARR M J, ROESSLER T, ROBINSON P W, et al. Calibration procedure of discrete element method (DEM) parameters for wet and sticky bulk materials[J]. Powder Technology, 2023, 429: 118919.
[6] 刘凡一, 张舰, 李博, 等. 基于堆积试验的小麦离散元参数分析及标定[J]. 农业工程学报, 2016, 32(12): 247-253.LIU Fanyi, ZHANG Jian, LI Bo, et al. Calibration of parameters of wheat required in discrete element method simulation based on repose angle of particle heap[J]. Transactions of the CSAE, 2016, 32(12): 247-253. (in Chinese)
[7] UCGUL M, FIELKE J M, SAUNDERS C. Three-dimensional discrete element modelling of tillage: determination of a suitable contact model and parameters for a cohesionless soil[J]. Biosystems Engineering, 2014, 121: 105-117.
[8] JIANG W, WANG L, TANG J, et al. Calibration and experimental validation of contact parameters in a discrete element model for tobacco strips[J]. Processes, 2022, 10(5): 998.
[9] 丁辛亭, 李凯, 郝伟, 等. 基于RSM和GA-BP-GA优化的油茶籽仿真参数标定[J]. 农业机械学报, 2023, 54(2): 139-150.DING Xinting, LI Kai, HAO Wei, et al. Calibration of simulation parameters of Camellia oleifera seeds based on RSM and GA-BP-GA optimization[J]. Transactions of the Chinese Society for Agricultural Machinery,2023, 54(2): 139-150. (in Chinese)
[10] 袁全春, 徐丽明, 邢洁洁, 等. 机施有机肥散体颗粒离散元模型参数标定[J]. 农业工程学报, 2018, 34(18): 21-27. YUAN Quanchun, XU Liming, XING Jiejie, et al. Parameter calibration of discrete element model of organic fertilizer particles for mechanical fertilization[J]. Transactions of the CSAE, 2018, 34(18): 21-27. (in Chinese)
[11] ROESSLER T, RICHTER C, KATTERFELD A, et al. Development of a standard calibration procedure for the DEM parameters of cohesionless bulk materials—part I: solving the problem of ambiguous parameter combinations[J]. Powder Technology, 2019, 343: 803-812.
[12] HORABIK J, MOLENDA M. Parameters and contact models for dem simulations of agricultural granular materials: a review[J]. Biosystems Engineering, 2016, 147: 206-225.
[13] ZHAO H, HUANG Y, LIU Z, et al. Applications of discrete element method in the research of agricultural machinery: a review[J]. Agriculture, 2021, 11(5): 425.
[14] XIA R, LI B, WANG X, et al. Measurement and calibration of the discrete element parameters of wet bulk coal[J]. Measurement, 2019, 142: 94-95.
[15] LEBLICQ T, SMEETS B, RAMON H, et al. A discrete element approach for modelling the compression of crop stems[J]. Computers and Electronics in Agriculture, 2016, 123: 80-88.
[16] THAKUR S C, MORRISSEY J P, SUN J, et al. Micromechanical analysis of cohesive granular materials using the discrete element method with an adhesive elasto-plastic contact model[J]. Granular Matter, 2014, 16(3): 383-400.
[17] JANDA A, OOI J Y. DEM modeling of cone penetration and unconfined compression in cohesive solids[J]. Powder Technology, 2016, 293: 60-68.
[18] ZHANG Z, MEI F, XIAO P, et al. Discrete element modelling and simulation parameters calibration for the compacted straw cube[J]. Biosystems Engineering, 2023, 230: 301-312.
[19] DING X, WEI Y, YAN Z, et al. Simulation and experiment of the spiral digging end-effector for hole digging in plug tray seedling substrate[J]. Agronomy, 2022, 12(4): 779.
[20] 中华人民共和国农业部. 蔬菜穴盘育苗: NY/T 2119—2012[S]. 北京: 中国农业科学技术出版社, 2014.
[21] 中华人民共和国水利部. 土工试验方法标准: GB/T 50123—2019[S]. 北京: 中国计划出版社, 2019.
[22] SHMULEVICH I. State of the art modeling of soil-tillage interaction using discrete element method[J]. Soil and Tillage Research, 2010, 111(1): 41-53.
[23] WANG X, ZHANG S, PAN H B, et al. Effect of soil particle size on soil-subsoiler interactions using the discrete element method simulations[J]. Biosystems Engineering, 2019, 182: 138-150.
[24] CHENG Y P, NAKATA Y, BOLTON M D. Discrete element simulation of crushable soil[J]. Geotechnique, 2003, 53(7): 633-641.
[25] 温翔宇, 袁洪方, 王刚, 等. 颗粒肥料离散元仿真摩擦因数标定方法研究[J]. 农业机械学报, 2020, 51(2): 115-122, 142. WEN Xiangyu, YUAN Hongfang, WANG Gang, et al. Calibration method of friction coefficient of granular fertilizer by discrete element simulation[J]. Transactions of the Chinese Society for Agricultural Machinery, 2020, 51(2): 115-122, 142. (in Chinese)
[26] 张胜伟, 张瑞雨, 陈天佑, 等. 绿豆种子离散元仿真参数标定与排种试验[J]. 农业机械学报, 2022, 53(3): 71-79.ZHANG Shengwei, ZHANG Ruiyu, CHEN Tianyou, et al. Calibration of simulation parameters of mung bean seeds using discrete element method and verification of seed-metering test[J]. Transactions of the Chinese Society for Agricultural Machinery, 2022, 53(3): 71-79. (in Chinese)
[27] HAN L H, ELLIOTT J A, BENTHAM A C, et al. A modified drucker-prager cap model for die compaction simulation of pharmaceutical powders[J]. International Journal of Solids and Structures, 2008, 45(10): 3088-3106.
[28] KARKALA S, DAVIS N, WASSGREN C, et al. Calibration of discrete-element-method parameters for cohesive materials using dynamic-yield-strength and shear-cell experiment[J]. Processes, 2019,75(5):278.
[29] THAKUR S C, MORRISSEY J P, SUN J, et al. Micromechanical analysis of cohesive granular materials using the discrete element method with an adhesive elasto-plastic contact model[J]. Granular Matter, 2014, 16(3): 383-400.
[30] 王宪良, 钟晓康, 耿元乐,等. 基于离散元非线性弹塑性接触模型的免耕土壤参数标定[J]. 农业工程学报, 2021, 37(23): 100-107.WANG Xianliang, ZHONG Xiaokang, GENG Yuanle, et al. Construction and parameter calibration of the nonlinear elastoplastic discrete element model for no-tillage soil compaction[J]. Transactions of the CSAE, 2021, 37(23): 100-107. (in Chinese)
[31] 谢方平, 吴正阳, 王修善, 等. 基于无侧限抗压强度试验的土壤离散元参数标定[J]. 农业工程学报, 2020, 36(13): 39-47.XIE Fangping, WU Zhengyang, WANG Xiushan, et al. Calibration of discrete element parameters of soils based on unconfined compressive strength test[J]. Transactions of the CSAE, 2020, 39(13): 39-47. (in Chinese)
[32] WANG Y, ZHANG Y, YANG Y, et al. Discrete element modelling of citrus fruit stalks and its verification[J]. Biosystems Engineering, 2020, 200: 400-414.
[33] HU Y, XIANG W, DUAN Y, et al. Calibration of ramie stalk contact parameters based on the discrete element method[J]. Agriculture, 2023, 13(5): 1070.
[34] 石林榕, 赵武云, 孙伟. 基于离散元的西北旱区农田土壤颗粒接触模型和参数标定[J]. 农业工程学报, 2017, 33(21): 181-187.SHI Linrong, ZHAO Wuyun, SUN Wei. Parameter calibration of soil particles contact model of farmland soil in northwest arid region based on discrete element method[J]. Transactions of the CSAE, 2017, 33(21): 181-187. (in Chinese)
[35] 武涛, 黄伟凤, 陈学深, 等. 考虑颗粒间黏结力的黏性土壤离散元模型参数标定[J]. 华南农业大学学报, 2017,38(3): 93-98.WU Tao, HUANG Weifeng, CHEN Xueshen, et al. Calibration of discrete element model parameters for cohesive soil considering the cohesion between particles[J]. Journal of South China Agricultural University, 2017, 38(3): 93-98. (in Chinese)
[36] 向伟, 吴明亮, 吕江南, 等. 基于堆积试验的黏壤土仿真物理参数标定[J]. 农业工程学报, 2019, 35(12): 116-123.XIANG Wei, WU Mingliang, LÜ Jiangnan, et al. Calibration of simulation physical parameters of clay loam based on soil accumulation test[J]. Transactions of the CSAE, 2019, 35(12): 116-123. (in Chinese)
[37] 张锐, 韩佃雷, 吉巧丽, 等. 离散元模拟中沙土参数标定方法研究[J]. 农业机械学报, 2017, 48(3): 49-56.ZHANG Rui, HAN Dianlei, JI Qiaoli, et al. Calibration methods of sandy soil parameters in simulation of discrete element method[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(3): 49-56. (in Chinese)