OSID：
集成串、并联机构混联机器人因兼具大工作空间、高运动灵巧度、高结构刚度等性能特点,已被Tricept、Eco-Speed和Exechon等高性能5轴混联加工机器人采用[1-4]。在航空、汽车和机械装备制造领域中,5轴混联机器人已成为其复杂结构件的重要加工装备[5-6]。结合Exechon中关节过约束布置特征[3]和Eco-Speed中并联模块的外副驱动形式[4],张俊等[7]提出了一种构型为2PRU&1PRS-XY型(R、P、U和S分别表示转动副、移动副、虎克铰和球铰)的新型混联机器人,并尝试将其用于5轴机械加工。为实现这一目标,除了明确其自由度、逆运动学、奇异性、工作空间、运动/力传递性以及灵巧度等运动学性能[8-13],还需要开展兼顾多个运动学性能指标的尺度设计,以获得多目标均衡优化的高性能混联机器人。
并/混联机构尺度设计方法主要有:性能图谱法[14]和目标函数法[15]。性能图谱法能够利用有限的空间图形,表示机构性能指标与设计参数之间的全域映射规律。马春生等[16]针对3-RPS并联机构,采用性能图谱法得到了该机构基于零件拆卸任务的优化方案。李研彪等[17]基于性能图谱法提出一种参数优化设计方法,通过综合多项性能指标,实现结构参数优化。刘晓飞等[18]提出一种多冗余并联机构,基于性能图谱法对机构的传递性能进行优化设计。性能图谱法具有很强的直观性,但需反复调用原函数,运算效率相对较低。目标函数法通过建立机构性能指标与尺度设计参数之间的数学表达式,并选用合适的优化算法,以找寻目标函数的最优解。LEI 等[19]将3-RRPS并联机器人的综合分支长度作为目标函数进行优化,得到的机构可用于盆骨折缩手术。王启明等[20]通过指标间的相关性,利用工作空间为目标函数得到了优化模型。目标函数法运算效率高且比较简便,但优化过程并不直观。此外,为满足日益多样化的结构和工程设计需求,学术界先后提出工作空间性能、运动/力传递与约束性能、灵巧度、奇异性等多种性能评价指标,为并/混联机器人的尺度设计提供了量化依据[21-25]。在量化评估的基础上,如何提炼能反映机器人在工作全域性能指标的稳定性与差异性的全局指标,以及如何进一步实现多目标高效优化与解集合理筛选,对开展并/混联机器人的多目标均衡优化至关重要。
本文提出一种兼顾直观表达和高效计算需求的混联机器人尺度设计方法,以期实现混联机器人多目标均衡优化。以所提2PRU&1PRS-XY型混联机器人为研究对象。首先,阐述新型混联机器人并定义坐标系,明确其自由度类型、逆运动学模型、运动解耦性,分析其工作空间及其内的运动/力传递性以及灵巧度分布情况,并定义传递稳定性指标和精度差异性指标。在此基础上,采用主成分分析法与响应面法提高多目标优化效率,结合基于TOPSIS的Pareto前沿法开展此类混联机器人的多目标均衡优化设计。
如图1所示,该混联机器人由构型为2PRU-1PRS的并联模块和交叉布置的串联模块构成。并联模块包括2条PRU支链和1条PRS支链,其中:PRU支链依次通过移动副、转动副和虎克铰连接机架和动平台,PRS支链依次通过移动副、转动副和球铰连接机架和动平台。3条支链以PRS支链为轴线呈等腰直角三角形分布,均由伺服电机连接丝杆导轨驱动。2条PRU支链结构尺寸相同,且关于PRS支链对称分布。串联模块由2个相互垂直交叉的移动滑轨构成,用于承载、驱动工件平台。串联模块通过机架与并联模块相连接,组成串-并混联机构。
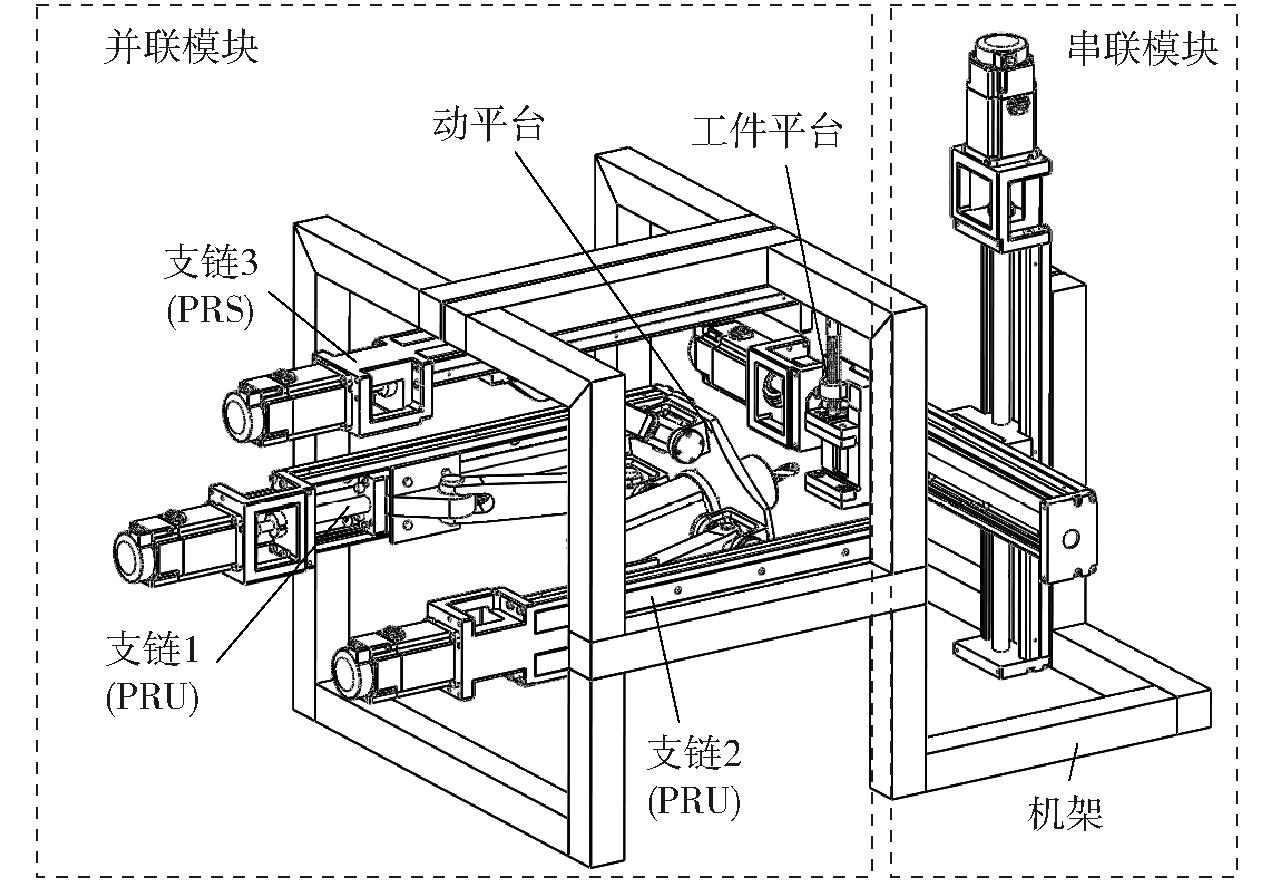
图1 混联机器人概念设计
Fig.1 Concept design of hybrid robot
为便于分析,定义如图2所示的系统坐标系Oxyz、局部坐标系O′uvw和移动坐标系Px0y0z0。
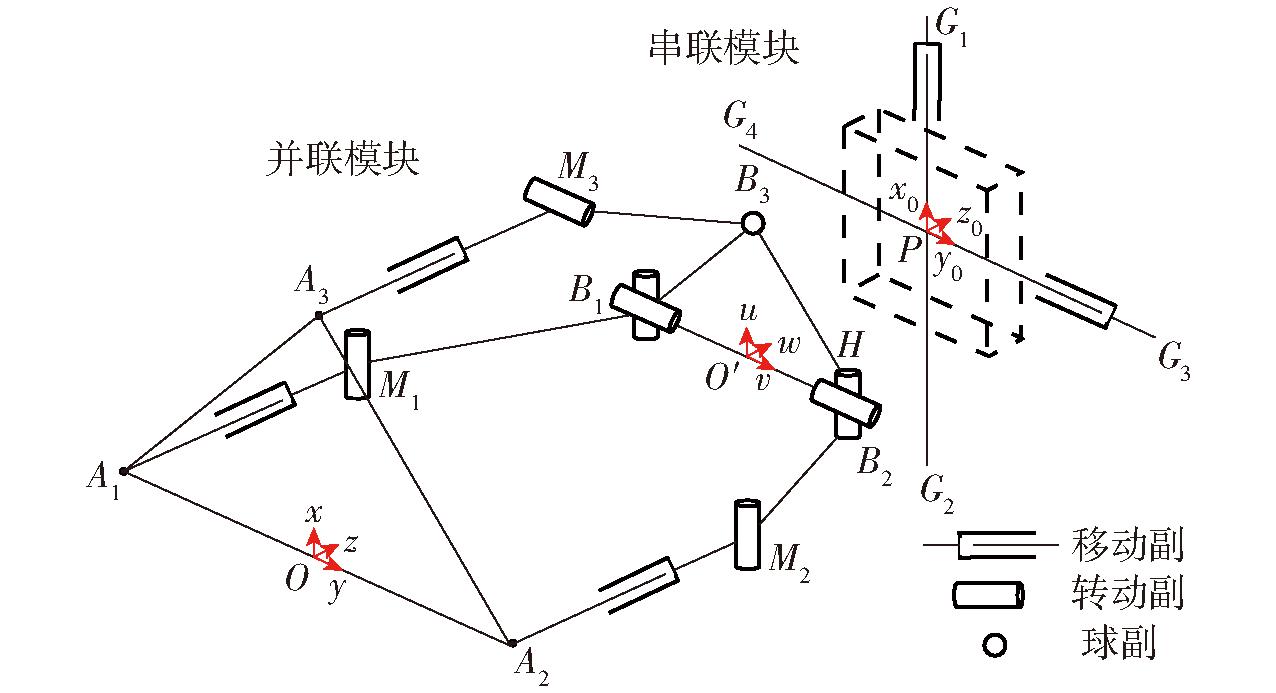
图2 机构简图
Fig.2 Schematic of mechanism
图2中,Ai(i=1,2,3)表示支链i上移动副的起点位置;Bi(i=1,2,3)表示支链i与动平台连接运动副的几何中心;Mi(i=1,2,3)表示支链i中转动副与移动副相连接的几何中心;Gi(i=1,2,3,4)表示串联模块中移动副的可达边界。系统坐标系Oxyz的原点O定义在A1A2的线段中心,x轴由O指向A3,y轴由O指向A2,z轴由右手定则确定;局部坐标系O′uvw的原点O′定义在B1B2的线段中点,u轴由O′指向B3,v轴由O′指向B2,w轴由右手定则确定;移动坐标系Px0y0z0的原点P定义在工件平台几何中心,x0轴由P指向G1,y0轴由P指向G3,z0轴由右手定则确定。
根据螺旋理论[26],定义$i1(i=1,2,3)为支链i上P副的运动螺旋,$i2(i=1,2,3)为支链i上R副转轴的运动螺旋,$i3(i=1,2,3)和$i4(i=1,2,3)分别为支链i上U副和S副第1和第2转轴的运动螺旋,$i5为支链i上S副第3转轴的运动螺旋。sik和rik分别表示支链i上第k个运动关节的单位向量和位置向量。
根据以上旋量系定义,可得支链1与支链2的运动螺旋系为
(1)
对式(1)求反螺旋系得
(2)
其中
sm=sm3×sm4
式中 
方向垂直于U副两交叉转轴的约束力偶
作用于U副两转轴中心并且方向平行于R副轴线的约束力
支链3运动螺旋系可表示为
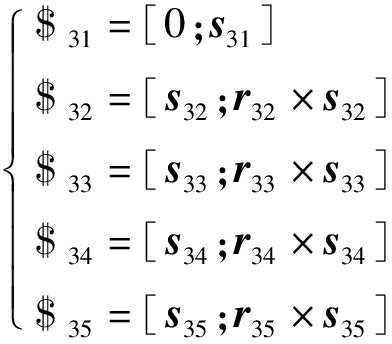
(3)
对式(3)求反螺旋可得
(4)
式中
作用点为S副几何中心且方向平行于R副转轴的约束力
通过支链的运动关节分布可知,当支链中的R副旋转角为90°时,将会使运动螺旋系产生线性相关,从而导致该支链的约束螺旋增加。
根据式(2)、(4)可得并联模块约束螺旋系为
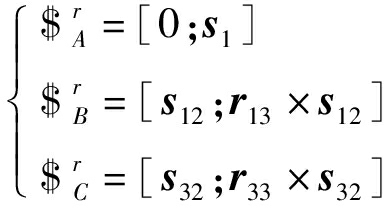
(5)
对式(5)求反螺旋可得并联模块动平台的运动螺旋系为
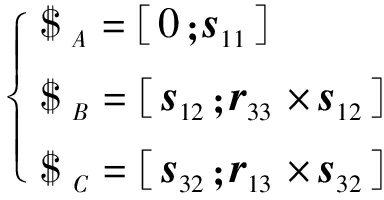
(6)
串联模块由2个相互垂直交叉的滑轨组成,其运动螺旋系可写为
(7)
式中 s4——沿滑轨1运动方向的单位向量
s5——沿滑轨2运动方向的单位向量
结合式(6)、(7)可得混联机构运动螺旋系为
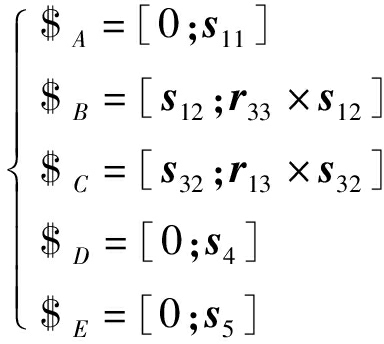
(8)
由式(8)可知,该混联机器人中并联模块的动平台相对于串联模块的工件平台具有5个运动自由度,即:沿向量s11、s4和s5方向的3个移动自由度以及绕通过U副中心且平行支链3上R副轴线和绕通过S副中心且平行支链1上R副轴线的2个转动自由度。
并联模块支链末端的瞬时运动螺旋可由支链中等效单自由度关节的运动旋量系表示,即
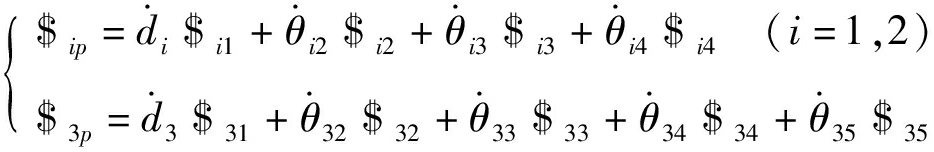
(9)
式中 
并联模块中第i条支链中移动副运动速率
第i条支链中第k个转动轴运动速率
将支链约束螺旋系分别与上述对应运动螺旋作互易积,可得
Jc1$p0=0
(10)
其中
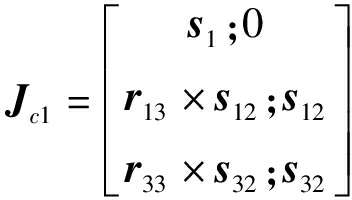
(11)
(12)
分别锁定3条支链上移动副,可得支链反螺旋为
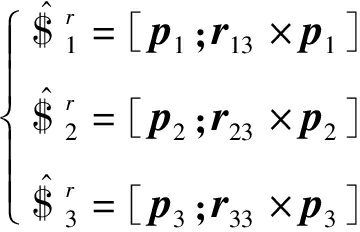
(13)
式中 pi——由Bi指向Mi的单位方向向量
将式(13)分别与上述对应运动螺旋作互易积得
(14)
其中
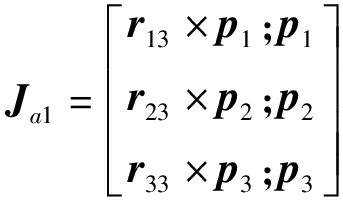
(15)
Jz=diag(pisi1) (i=1,2,3)
(16)
串联模块由2条滑轨垂直交叉而成,因此其运动螺旋可表示为
(17)
式中 
串联滑轨1运动速率
串联滑轨2运动速率
分别锁定串联模块的2个移动副,可得支链的反螺旋并与式(17)作互易积,其矩阵形式为
(18)
其中
(19)
结合式(10)、(14)、(19)可得混联机构运动旋量表达式为
J$′p=d′
(20)
其中
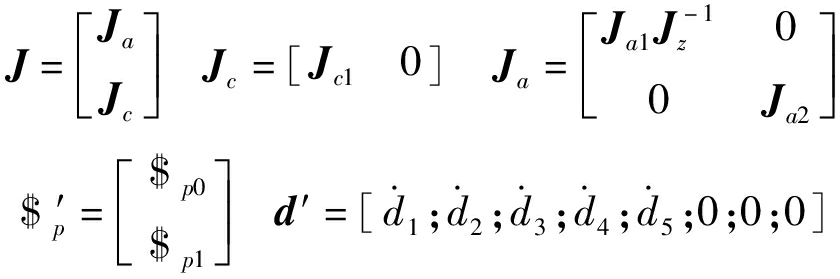
式中 J——混联机构的全雅可比矩阵
通过分析全雅可比矩阵J的秩可知:
(1)矩阵Ja中,前3行表示通过各支链U副或S副转动中心并与向量p1、p2、p3平行的约束力。当上述向量共面时会产生结构奇异,可通过结构设计避免此情况。
(2)矩阵Jc中,s1、s12、s32之间相互独立,因此矩阵Jc各行列线性无关,即该混联机器人不存在约束奇异。
(3)特别地,当转动副转角为90°时,支链运动螺旋发生线性相关,机构将会产生运动支链奇异,需要在轨迹规划中避免此情况。
建立如图3所示的混联机器人闭环矢量图。图中q表示在Oxyz坐标系中点O′的位置向量;h表示在坐标系O′uvw中刀头顶点H的位置向量;rai(i=1,2,3)表示在坐标系Oxyz中点Ai的位置向量;rbi(i=1,2,3)表示在坐标系O′uvw中点Bi的位置向量;wi(i=1,2,3)表示在坐标系Oxyz中从点Ai指向Mi的单位向量;li(i=1,2,3)表示支链i移动副长度;ai(i=1,2,3)表示在坐标系Oxyz中从Mi指向Bi的向量;根据相对运动关系可以给出混联机器人机构的闭环矢量方程为
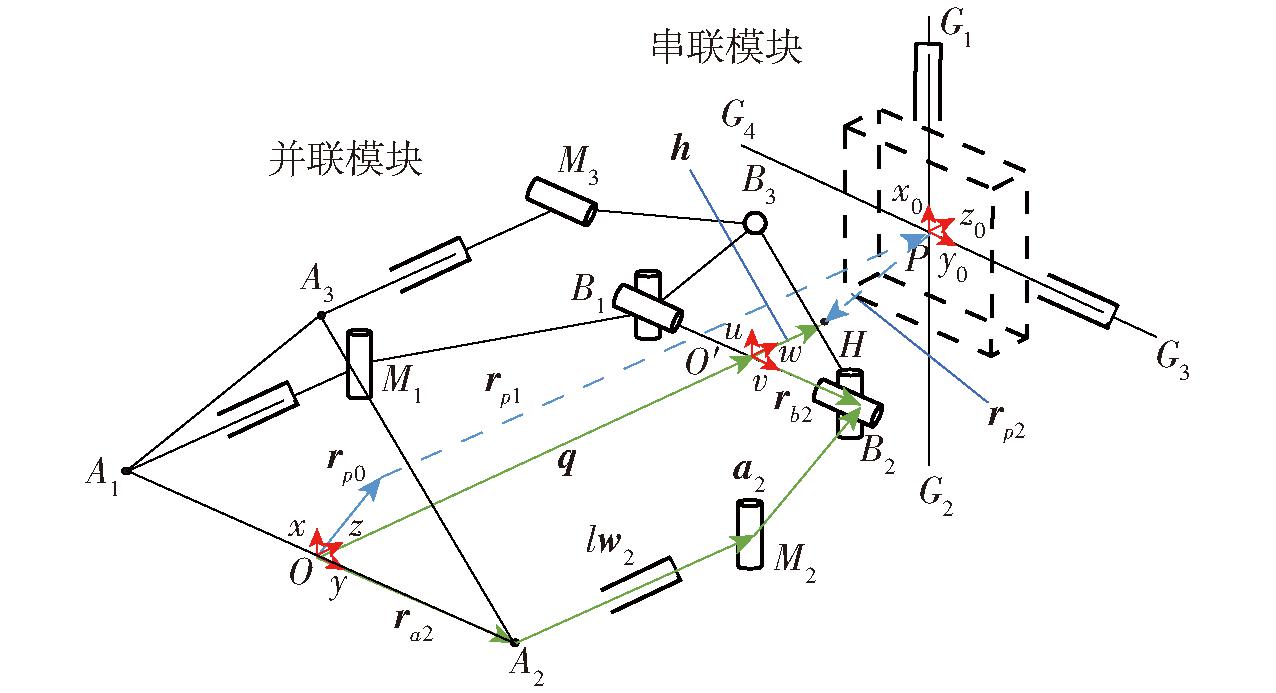
图3 支链闭环矢量图
Fig.3 Closed-loop vectors of limbs
rH=q+Th
(21)
其中
q=rai+lwi+ai-Trbi
T=Rx(ψ)Ry(θ)Rz(φ)=
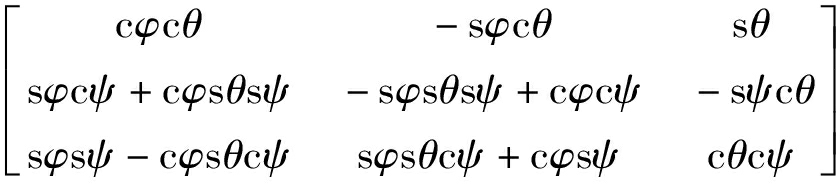
(22)
式中 rH——坐标系Oxyz中点H的位置向量
T——坐标系Oxyz和坐标系O′uvw之间的旋转矩阵
ψ——动平台平动角
θ——动平台章动角
φ——动平台自旋角
其中c和s分别代表cos和sin。
根据图3的虚线向量也可得闭环矢量方程为
rH=rp0+rp1+rp2
(23)
其中
rp0=[d4;d5;0] rp1=[0;0;n]
式中 d4——在Oxyz坐标系中点P的x轴坐标
d5——在Oxyz坐标系中点P的y轴坐标
n——在Oxyz坐标系中点P的z轴坐标
rp2——在Px0y0z0坐标系中点H的位置向量
结合式(21)和式(23)可得
rH=rai+lwi+ai-T(rbi-h)=rp0+rp1+rp2
(24)
根据该混联机器人结构特征,向量ra3与向量rb2相互垂直并且与向量q也相互垂直。此外,向量ra1与向量lw3和a3均垂直。由此,可将上述向量位置关系表达为
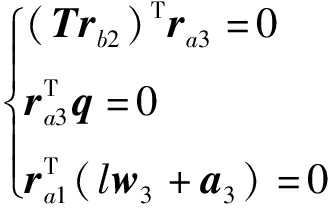
(25)
将式(21)代入式(25)可求得
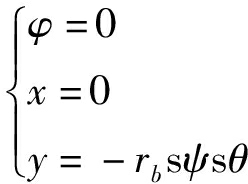
(26)
结合式(21)和式(26),可得
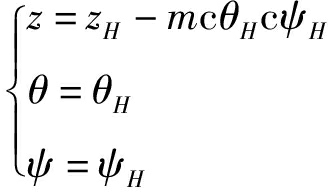
(27)
式中 x——点O′在坐标系Oxyz中的x轴坐标
y——点O′在坐标系Oxyz中的y轴坐标
z——点O′在坐标系Oxyz中的z轴坐标
zH——点H在坐标系Oxyz中的z轴坐标
θH——刀具末端章动角
ψH——刀具末端平动角
m——刀具长度
将式(26)和式(27)代入式(24)即可求得混联机器人的位置反解。不失一般性,可将刀具末端位姿参数(xH、yH、zH、θH、ψH)作为自变量,即可得
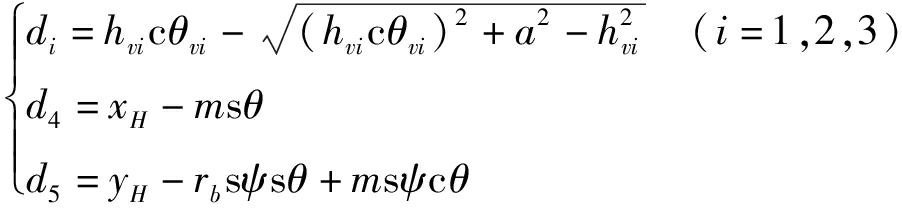
(28)
其中
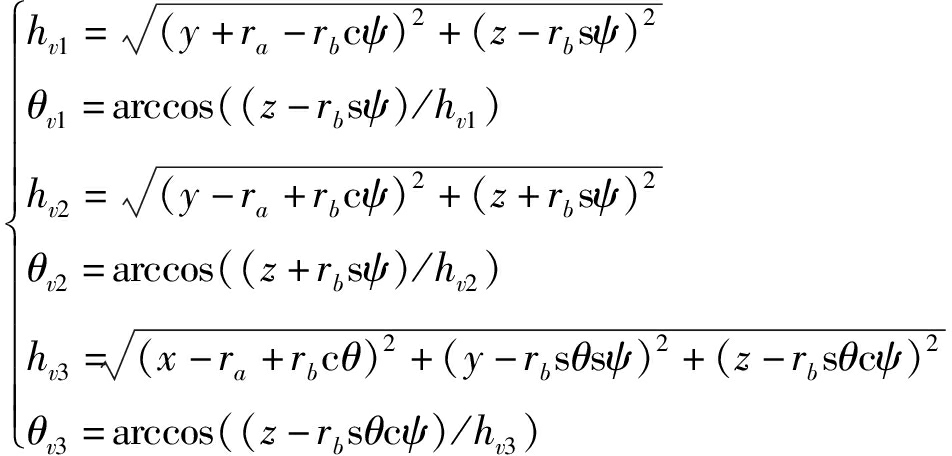
(29)
提出一种基于Solidworks运动仿真的机构运动解耦性判断方法。分析步骤如下:①利用Solidworks软件建立机构的三维模型。②根据机构自由度F,确定输入量di(i=l～n,n=F)。每次仅改变一个输入量dj,并赋予其不同的数值,同时固定其余输入量。经仿真计算,可获得不同输入量dj时的所有输出量。③借鉴文献[27]所提出的解耦性判别方法,若某一输出量随输入量dj的变化而变化,则表明该输出量与输入量dj有关,不具有运动解耦性,从而快速判别。
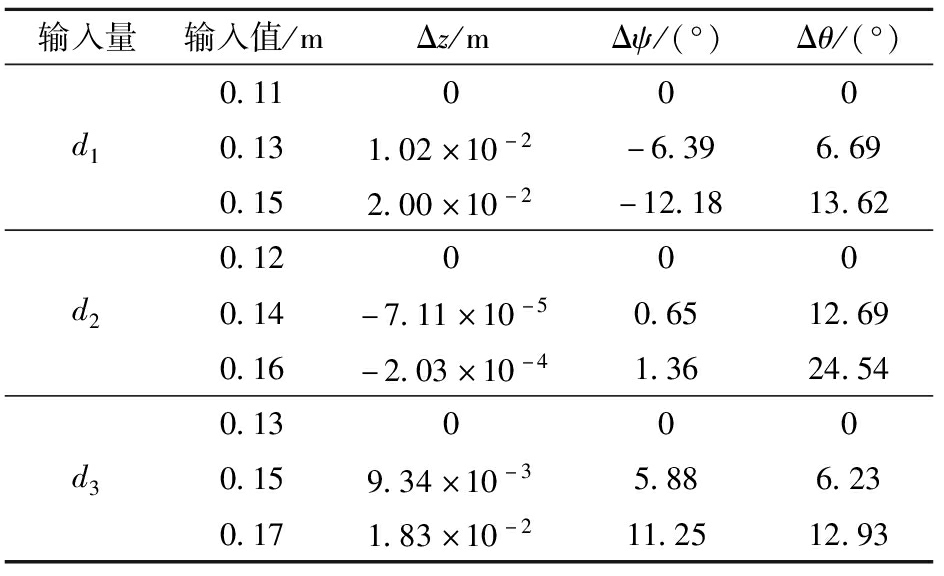
不失一般性,将输入量d1=0.11 m、d2=0.12 m、d3=0.13 m分别赋予驱动副作为初始输入量,并在三维模型中设定对应驱动量,依次改变其中一项输入量后统计所有输出变量的变化。
根据表1结果,输入量d1、d2、d3的变换均会导致3个输出变量发生不同程度的变化。因此,3个输出变量与各输入量之间有关,并联模块不具备运动解耦性。
表1 不同输入值的输出结果
Tab.1 Outputs at different input values
输入量输入值/mΔz/mΔψ/(°)Δθ/(°)0.11000d10.131.02×10-2-6.396.690.152.00×10-2-12.1813.620.12000d20.14-7.11×10-50.6512.690.16-2.03×10-41.3624.540.13000d30.159.34×10-35.886.230.171.83×10-211.2512.93
对于整个混联机构,其自由度为5(3T2R),输入量为d1、d2、d3、d4、d5,输出变量为末端位姿x、y、z、θ、ψ。根据式(26)～(28)可知,串联模块的输入d4、d5仅会影响运动末端的x、y方向位移,并联模块的运动不会改变坐标x,而会改变坐标y。因此,输出变量x仅与输入量d4相关,输出变量y与所有输入量均有关。亦即混联机构具有部分解耦性。
工作空间是并/混联机器人的关键性能指标之一。采用工作空间搜索法[28],可快速预估该5轴混联机器人的可达工作空间。其基本思路为:
(1)采用“分层切片”的基本思想,选取动平台姿态参数(x,y,z,ψ,θ)并将其分别进行等分,得到对应的位姿离散点。
(2)将离散点坐标依次代入前述位置逆解模型,求解各支链和关节的运动参数。
(3)判断所得支链和关节的运动参数是否符合其许用值,将许用范围内的位姿点记为可达空间点。
(4)循环执行步骤(1)～(3),直至遍历所有离散点。将所得可达空间点合集记为该混联机构的可达工作空间。
表2为该混联机器人的初始尺寸与运动关节许用转角。其中,ra为静平台中心到移动副的距离;rb为动平台中心到U副的距离;a为R副到U副/S副的连杆长度;lmax为移动副P的最大行程;θR、θU和θS分别为R副、U副和S副的最大许用转角。
表2 初始尺寸与运动关节许用转角
Tab.2 Initial dimensions and permissible angles of joints
参数ra/mrb/ma/mlmax/mθR/(°)θU/(°)θS/(°)数值0.160.090.180.30706565
采用前述工作空间搜索法,可分别定义并求得该5轴混联机器人的转动工作空间Vr和移动工作空间Vm,如图4、5所示。
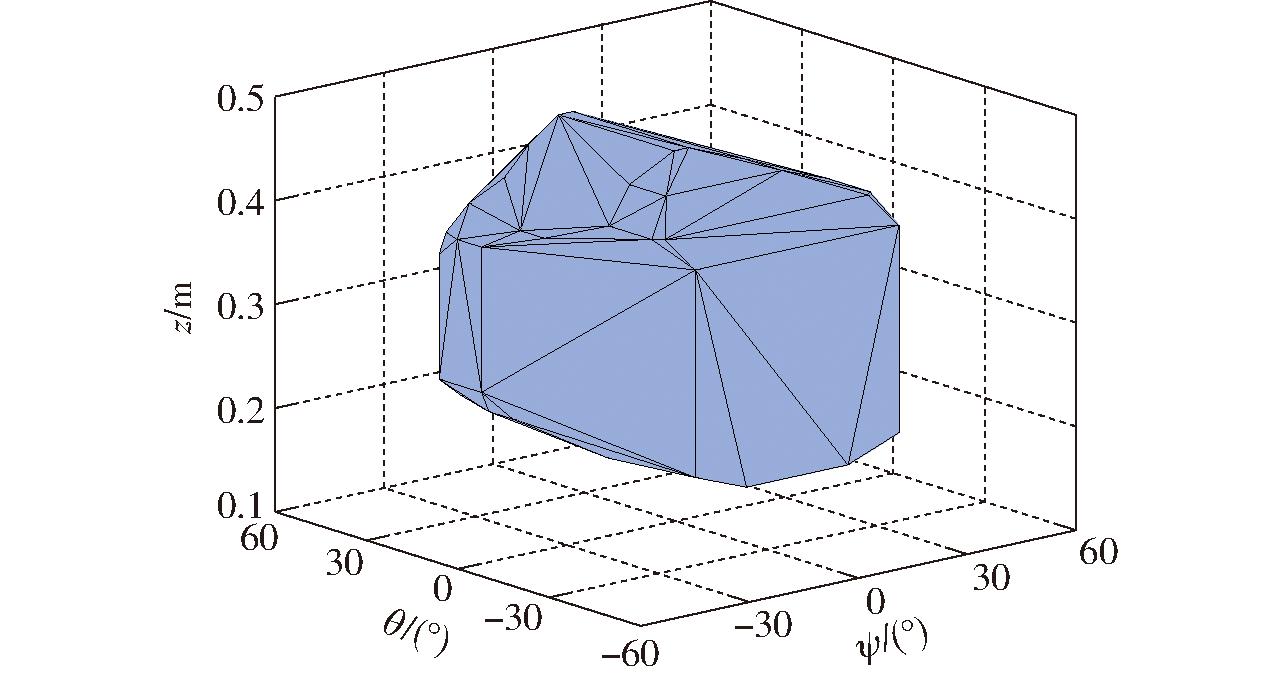
图4 转动工作空间
Fig.4 Orientation workspace
由图4可知,混联机器人中动平台平动角ψ的转动范围为-28°～28°,章动角θ的最大转动范围为-40°～34°,z轴最大移动范围为0.18～0.46 m,可达转动工作空间Vr为0.379 m·rad2。进一步观察可知,随坐标z的增大转角范围先增大后减小,且工作空间分布关于ψ=0°平面对称。这一现象与混联机构中并联模块对称的拓扑结构特征相一致,表明该混联机构的转动工作空间主要由其所含并联模块决定。
如图5所示,混联机器人移动工作空间表示并联模块动平台相对串联模块上工件平台的可达范围,其中:x轴方向的移动范围为-0.15～0.15 m,y轴方向的移动范围为-0.179～0.179 m,z轴方向的移动范围为0.18～0.46 m,可达移动工作空间Vm为0.033 m3。结合串联模块的行程参数,可知该串-并混联机构的移动工作空间主要由其所含串联模块决定。因此,须根据移动工作空间设计需求,选择合适的串联滑轨行程。
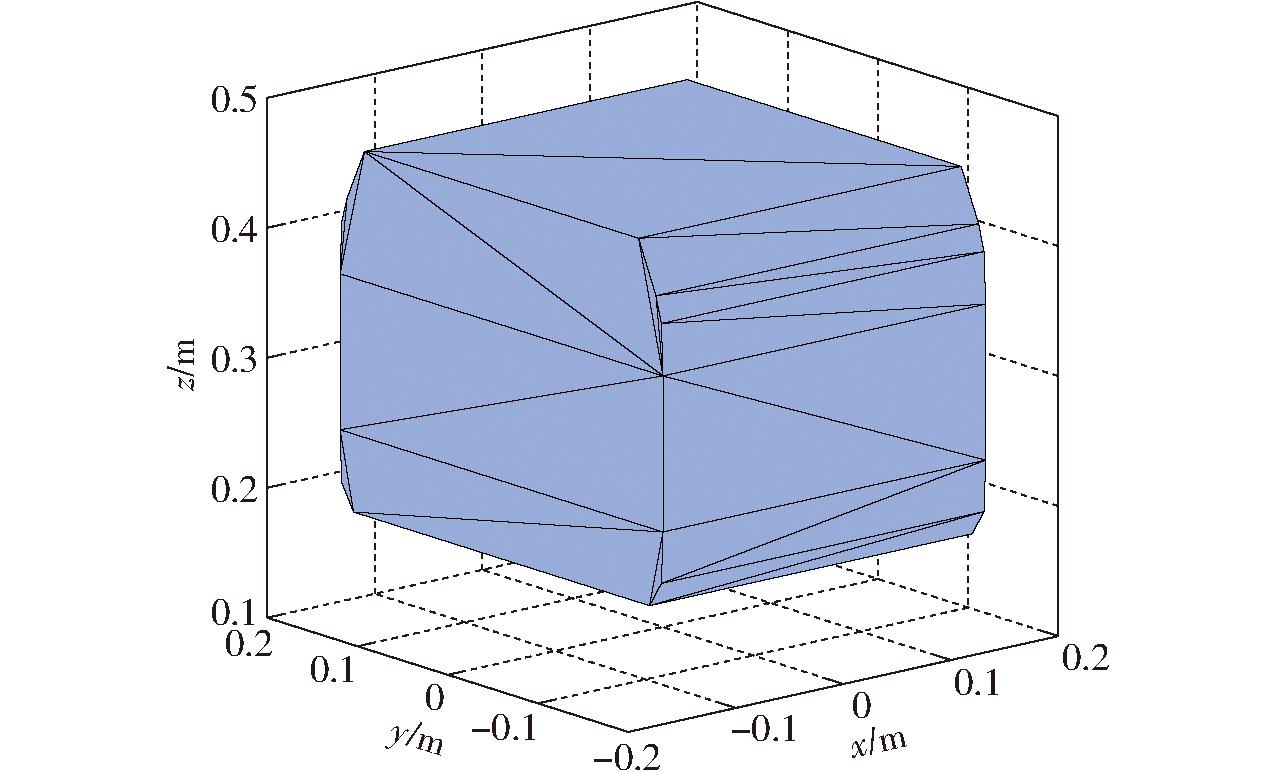
图5 移动工作空间
Fig.5 Position workspace
运动/力传递性指标被广泛应用于并/混联机构的性能分析与优化设计。根据文献[9-11]可分别定义输入传递指标η1、输出传递指标η2以及局部传递指标Γ计算公式为
(30)
(31)
Γ=min(η1,η2)
(32)
式中 $Ii——输入运动螺旋
$Ti——传递力螺旋
$Oi——输出运动螺旋
特别地,由于并联模块中3条支链的主动关节均为P副,故输入运动螺旋$Ii=$i1。力螺旋与支链中各个被动关节的运动螺旋互易积为0,且与约束螺旋系线性无关,各支链传递力螺旋可写为
$Ti=[pi;ri3×pi]
(33)
将除支链i之外的驱动副锁定,此时自由度仅为1,所得动平台的运动螺旋即为该支链的输出运动螺旋
(34)
式中 ni——Bk(k≠i)指向Bj(j≠i;j<k)的单位向量
向量ni的位置向量
将式(33)和式(34)代入式(30)～(32)可得局部传递指标分布。如图6所示,局部传递指标随动平台位姿的变化而变化,且谱图截面关于角度ψ=0°对称分布,与并联模块的结构对称性相一致。不失一般性,可将转动工作空间内Γ>0.70的位姿集合定义为优质传递空间。机构在优质传递空间内的位姿点处工作,可实现较好的运动/力传递性能。
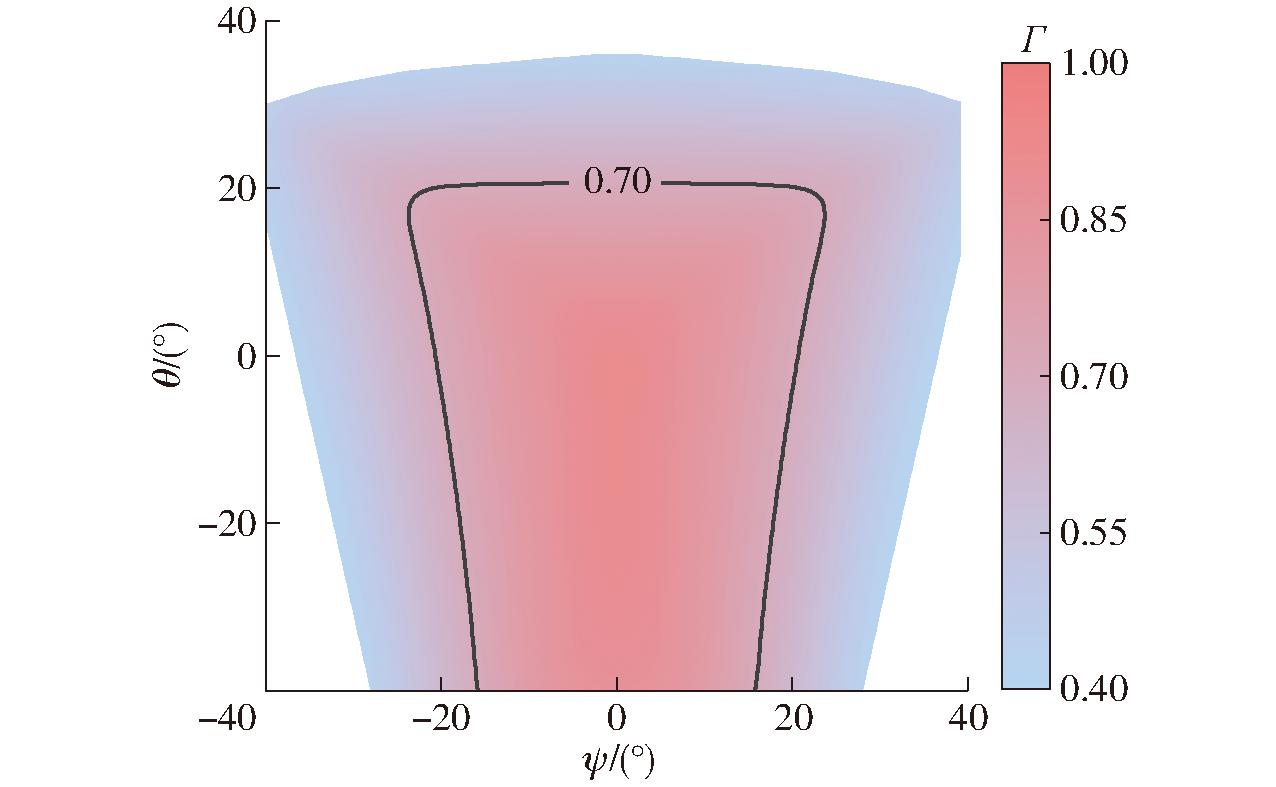
图6 局部传递指标分布图
Fig.6 Local transmission index distribution
由于局部传递指标随位姿变化,为便于整机优化设计,可定义优质工作空间占比ηG作为全局传递指标,计算公式为
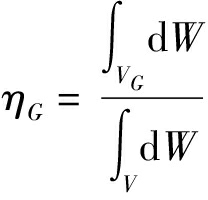
(35)
式中 V——可达工作空间体积
VG——优质工作空间体积
W——可达工作空间
经计算可得,机构在初始尺寸下全局传递指标为0.401。
在局部和全局传递性指标的基础上,为准确评估工作空间中运动/力传递稳定性,将工作空间中运动/力传递性指标的变异系数
定义为传递稳定性指标,计算公式为
(36)
式中 σG——工作空间中局部传递指标标准差
工作空间中局部传递指标平均值
经计算可得,在初始尺寸下机构传递稳定性指标为0.283。
灵巧度指标是衡量机构输入(运动/力)与输出之间传递精度的重要指标。结合全雅可比矩阵与逆运动学模型可推出输入运动速度与输出运动速度之间的映射关系为
(37)
其中
由于该机构自由度为混合自由度,需对雅可比矩阵进行无量纲化处理。利用特征长度法,将全雅可比矩阵的第2、3行除以动平台中心距rb,可得到无量纲雅可比矩阵为
(38)
一般采用机构雅可比矩阵条件数的倒数作为灵巧度的评价指标,即
(39)
其中
(40)
式中 kJ——雅可比矩阵的条件数
σM——雅可比矩阵Jx的谱范数
σm——雅可比逆矩阵
的谱范数
ηJ的取值范围为0～1。ηJ越小,机构运动传递精度越低。
如图7所示,局部灵巧度随动平台位姿的变化而变化,且分布图截面关于角度ψ=0°对称分布,与并联模块的结构对称性相一致。为衡量机构在其整个工作空间内的灵巧度,可将工作空间中各位姿对应的灵巧度平均值ηJm作为机构的全局灵巧度指标,其计算公式为
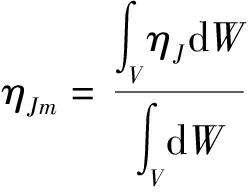
(41)
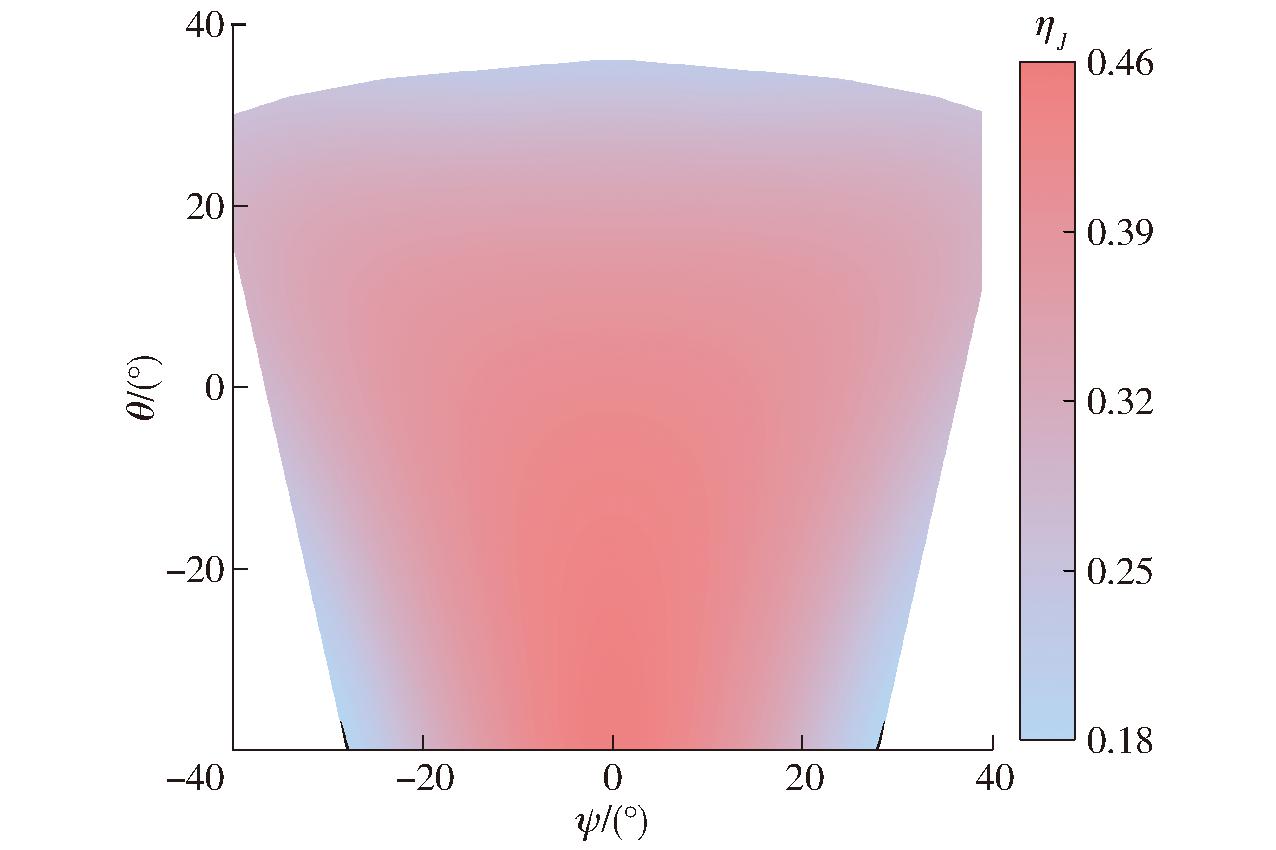
图7 局部灵巧度分布图
Fig.7 Local dexterity distribution
经计算可得,在初始尺寸下机构全局灵巧度指标为0.352。
为合理评估工作空间中不同位置之间的运动传递精度差异,揭示灵巧度的全局波动情况,将全域中灵巧度指标的变异系数定义为精度差异性指标,即
(42)
式中 σJ——工作空间中局部灵巧度标准差
ηJm——工作空间中局部灵巧度平均值
经计算可得,在初始尺寸下机构精度差异性指标为0.168。
机构性能受结构设计参数的影响不尽相同,各性能指标之间也往往相互关联,须在尺度设计阶段综合考虑多目标均衡设计,才能获得性能优良的混联机器人机构。为此,提出设计思路:首先,采用标准化方法处理尺度设计变量,得到三维和二维参数设计空间,便于进行参数规划。其次,采用响应面法拟合各性能指标函数并以此作为目标函数,避免原始功能函数的反复调用,提高计算效率。然后,通过主成分分析法,减少所需优化的指标数。最后,将主观赋权与客观赋权相结合以分辨各指标重要性,并采用基于TOPSIS法的Pareto前沿法实现非劣解的合理评分,由此筛选出符合工程设计偏好的均衡优化解。以所提方法开展2PRU&1PRS-XY型混联机器人的多目标均衡尺度设计。
由运动学分析可知,该混联机器人所需优化主要尺寸为ra、rb和a,标准化处理后可得
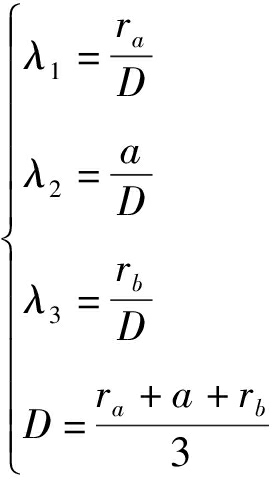
(43)
式中 D——标准化因子
λ1、λ2、λ3——无量纲参数
根据混联机器人机构几何约束关系和加工应用场景,无量纲参数λ1、λ2、λ3之间应满足
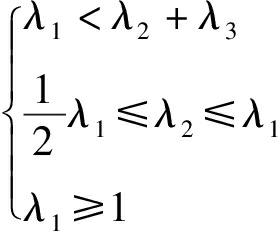
(44)
为保证混联机器人机构正常工作:①对于工作空间,应使得其有足够的加工能力,并联模块转动工作空间需能够包络转动工作空间GV。其中,GV指平动角ψ和章动角θ的可达范围是-25°～25°,z轴可达范围是0.25～0.35 m。②为确保机构运动/力传递性能,令全局传递指标大于0.6,传递稳定性指标小于0.21。③为避免过低的运动传递精度,可设全局灵巧度指标大于0.36,精度差异性指标小于0.19。综上,建立优化设计模型
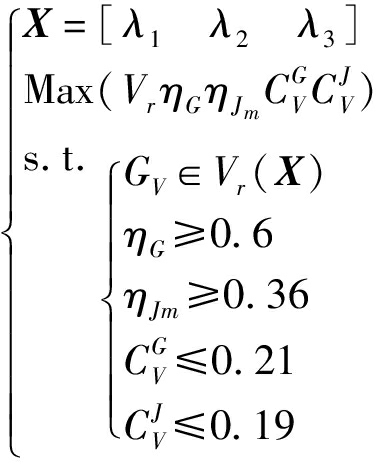
(45)
根据式(44)可绘制三维参数设计空间,如图8所示。其中,不规则四边形区域DEFG为三维参数设计区域。
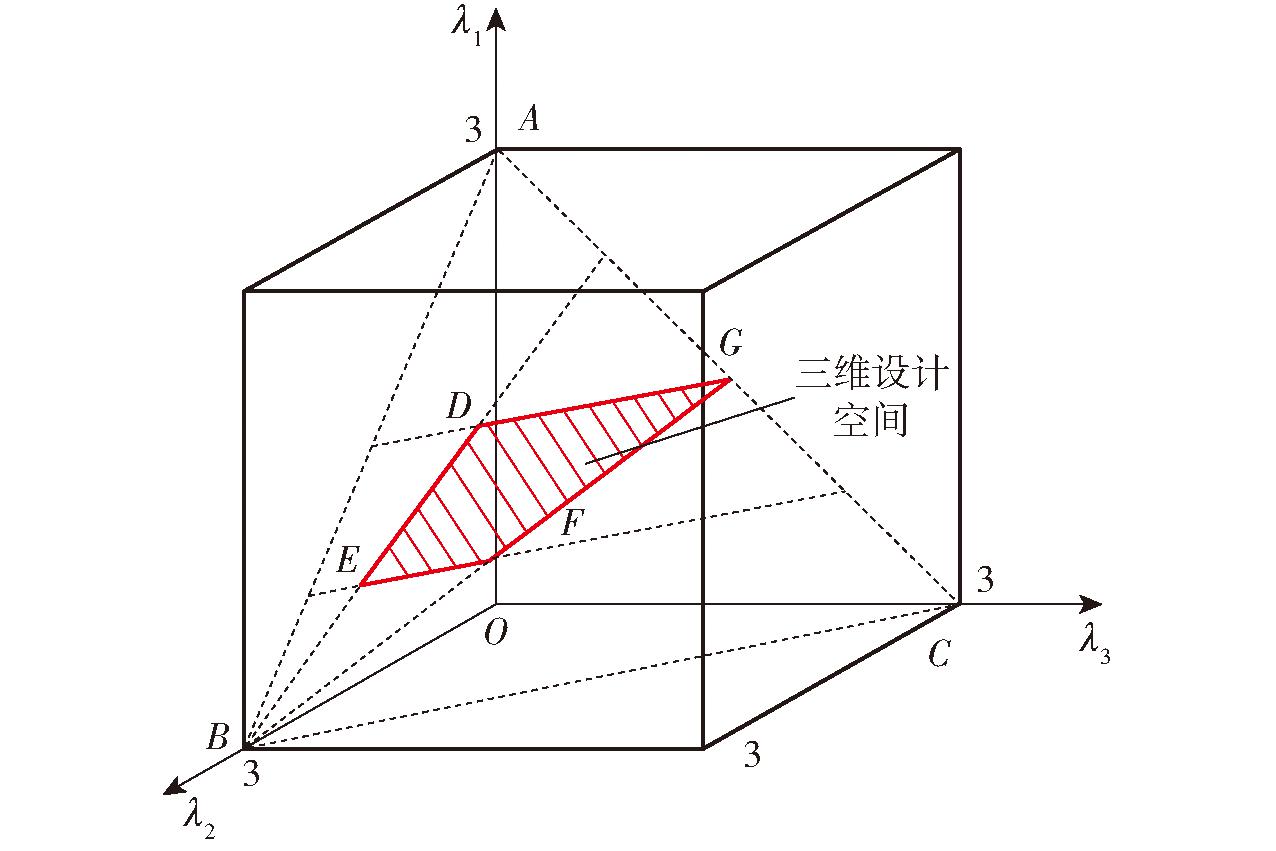
图8 三维参数设计空间
Fig.8 Three-dimensional parametric design space
当λ1、λ2、λ3中任意两项确定时,最后一项也可确定,故可采用λ1、λ2为独立变量进行优化。此时,三维参数设计空间转变为二维参数设计空间。如图9所示,四边形区即为所得二维参数设计区域。
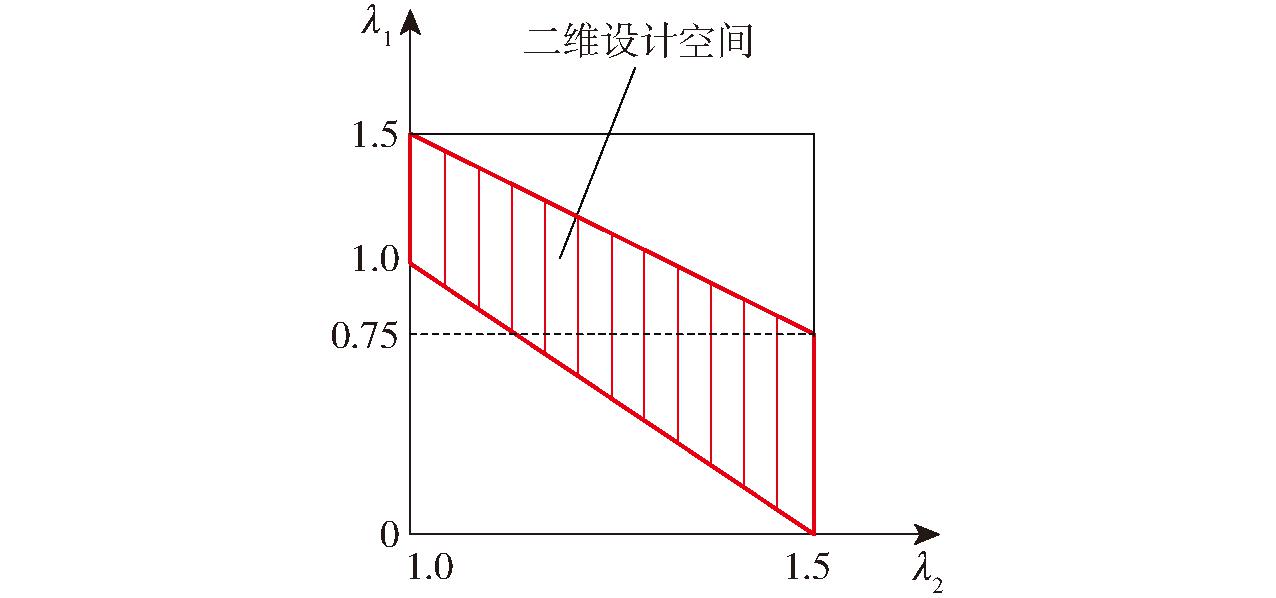
图9 二维参数设计空间
Fig.9 Two-dimensional parametric design space
为减少功能函数调用时间、便于快速优化迭代,采用响应面进行功能函数拟合。为此,将λ1等分为k个离散点,λ2按照取值范围等分为n份,由此得到m×n个离散点作为样本拟合数据点。采用Origin拟合工具箱进行响应面拟合,得到其响应面函数分别为
Vr=-161.657 67+284.814 87λ1+137.546 61λ2-
(46)
ηG=-45.061 66+83.948 68λ1+49.738 43λ2-
(47)
ηJm=7.054 8-10.594 61λ1-5.913 23λ2+
(48)
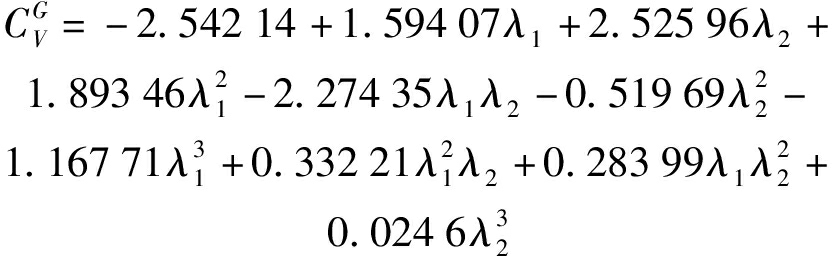
(49)
(50)
函数(46)～(50)对应的响应面如图10～14所示。
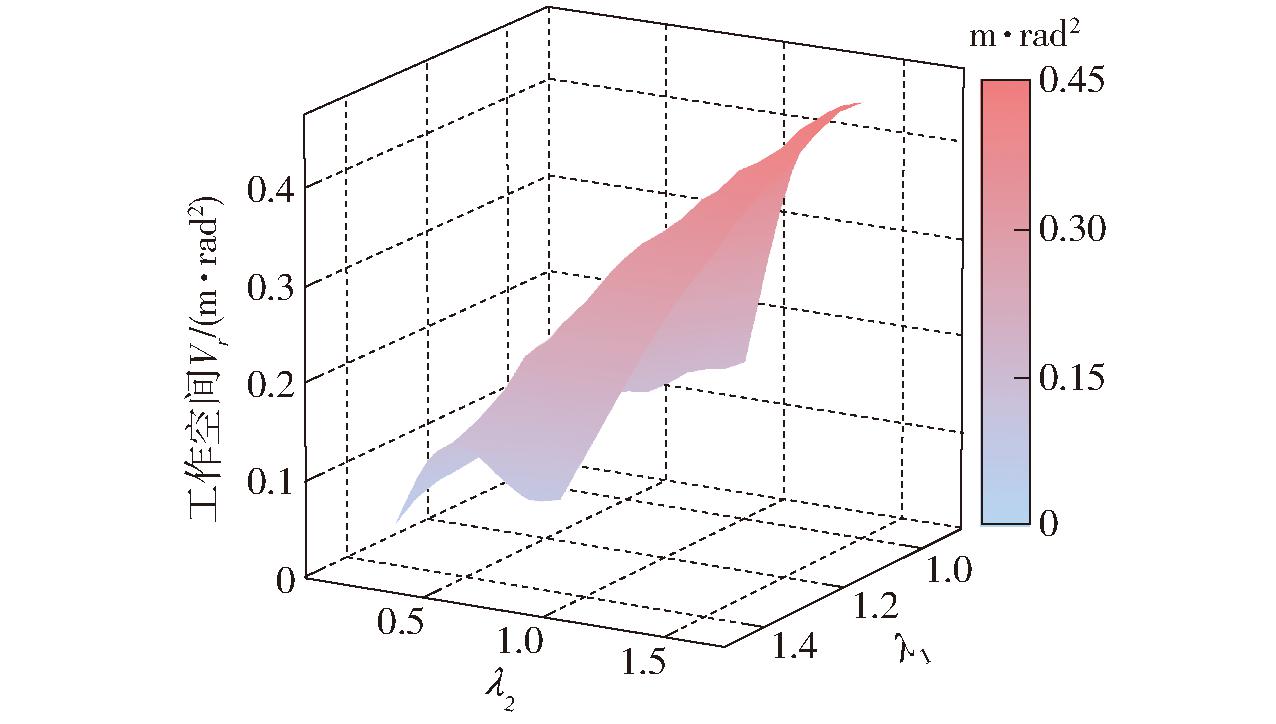
图10 工作空间响应面
Fig.10 Response surface of reachable workspace
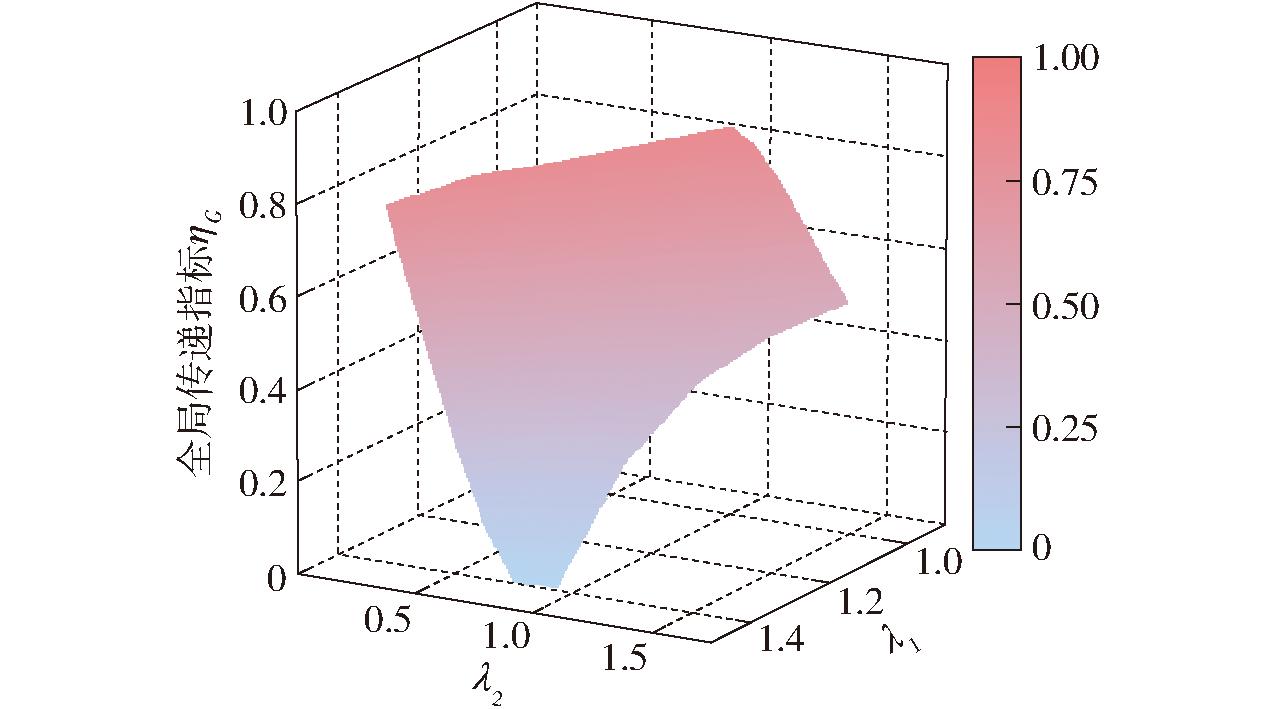
图11 全局传递指标响应面
Fig.11 Response surface of global transmission index
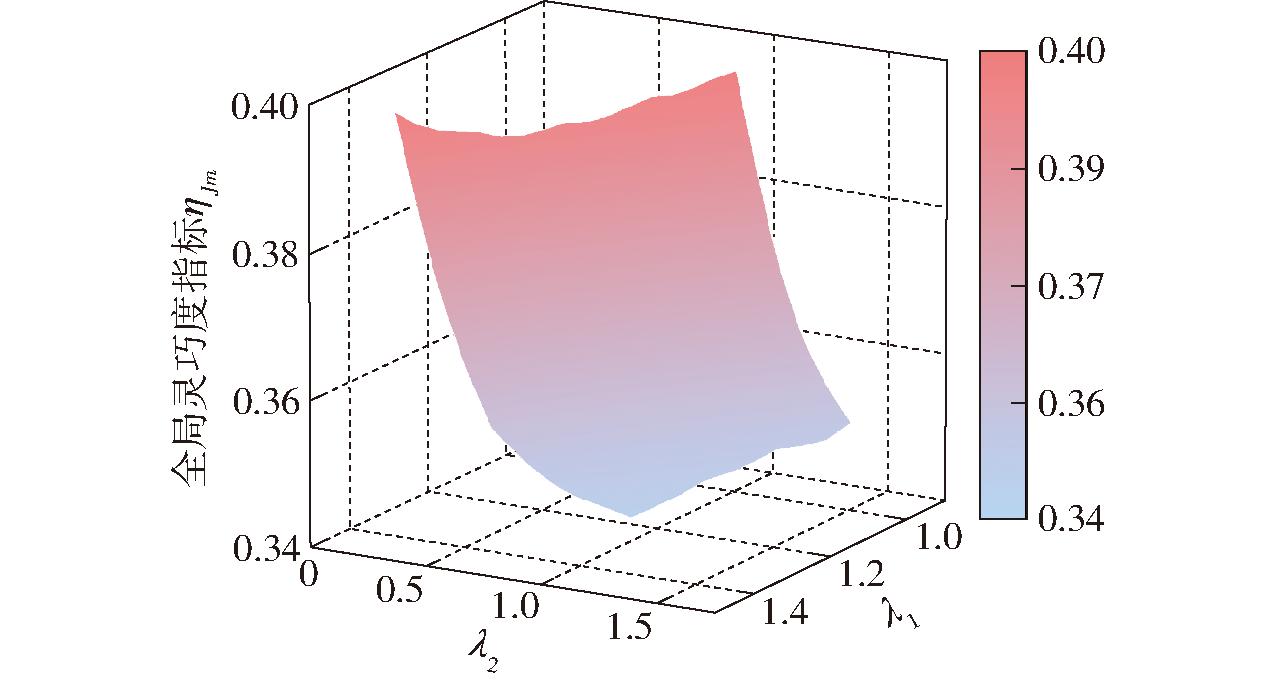
图12 全局灵巧度指标响应面
Fig.12 Response surface of global dexterity index
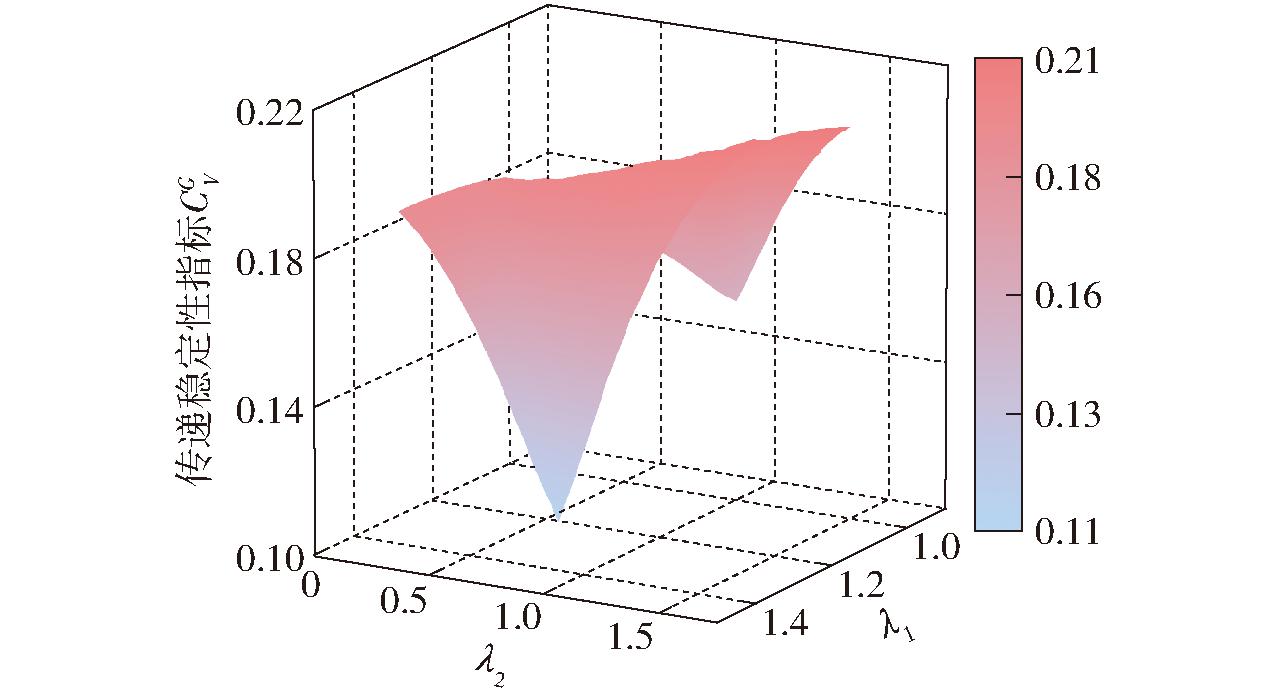
图13 传递稳定性指标
Fig.13 Transitive coefficient of variation
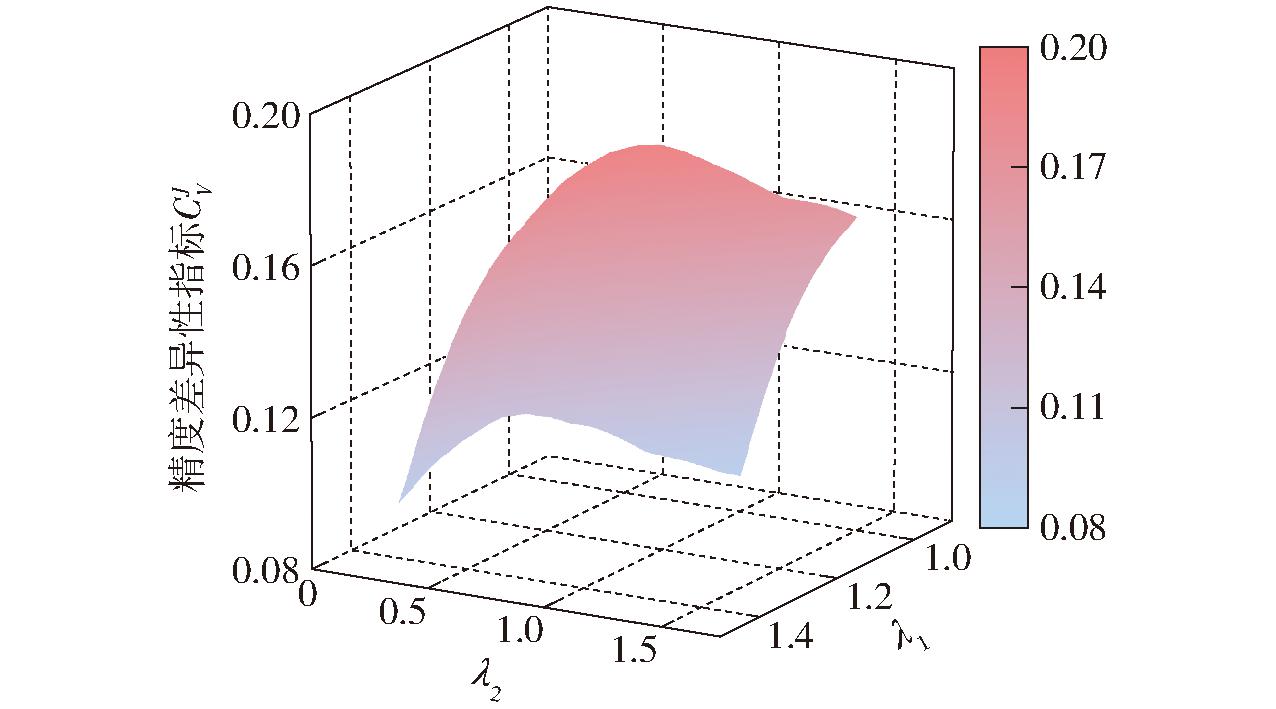
图14 精度差异性指标
Fig.14 Dexterity coefficient of variation
由于优化指标量纲与类型不同,需通过z正向化与标准化处理。令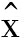
(i)表示第i个解处理后的指标参数,x(i)表示第i个解处理前的参数,
和
分别表示所有解集中当前指标的最优解和最劣解,则有
(51)
为提高优化运算效率,采用主成分分析法减少所需优化的指标数量。将传递性指标及其变异系数转换为传递性综合指标,将灵巧度指标及其变异系数转换为灵巧度综合指标。为此,建立变量相关矩阵
(52)
其中
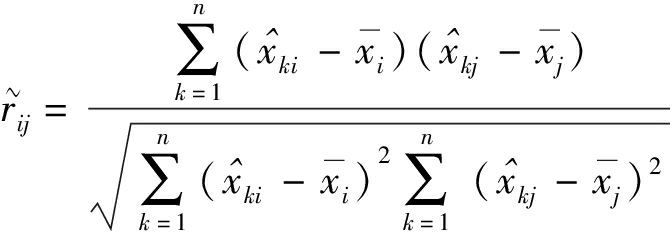
(i=1,2;j=1,2)
(53)
式中 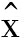ki——第i个指标的第k个样本
第i个指标和第j个指标的相关系数
求得Rc的特征值与特征向量,并计算各特征值的贡献率
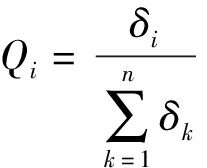
(54)
如表3所示,传递性综合指标主成分1贡献率为90.4%,主成分2贡献率为9.6%。灵巧度综合指标主成分1贡献率为98.9%,主成分2贡献率为1.1%。
表3 主成分分析结果
Tab.3 Principal component analysis results
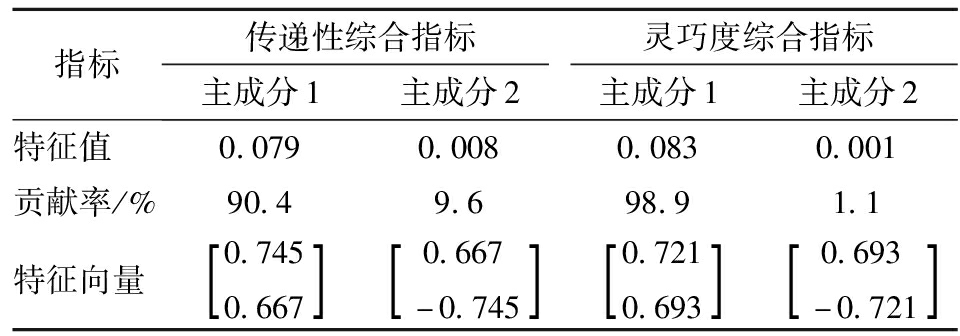
指标传递性综合指标灵巧度综合指标主成分1主成分2主成分1主成分2特征值0.0790.0080.0830.001贡献率/%90.49.698.91.1特征向量0.7450.667[]0.667-0.745[]0.7210.693[]0.693-0.721[]
据此,可以分别合并得到传递性综合指标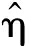
G和灵巧度综合指标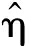Jm为
(55)
(56)
式中 b1、b2——传递性综合指标的特征向量系数
c1、c2——灵巧度综合指标的特征向量系数
为缓解不同指标之间的强度与冲突性不同对评分结果造成的影响,采用CRITIC法进行赋权。其中,指标强度用标准差σj体现,指标间冲突性用关联系数rij体现。经计算,工作空间指标Vr标准差为0.227 m·rad2;传递性综合指标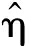G标准差为0.215;灵巧度综合指标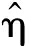Jm标准差为0.204。各指标之间的相关系数见表4。
表4 指标相关系数
Tab.4 Indicator correlation coefficients
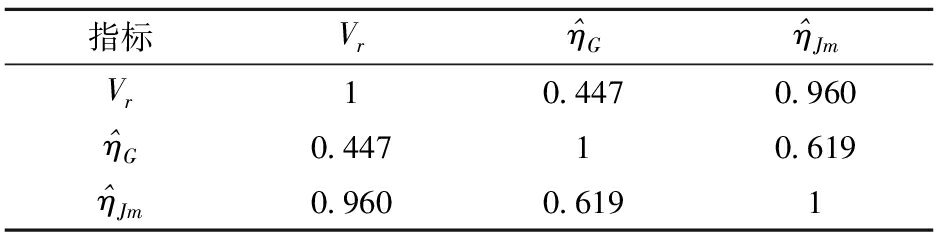
指标Vr^ηG^ηJmVr10.4470.960^ηG0.44710.619^ηJm0.9600.6191
将上述结果代入公式
(57)
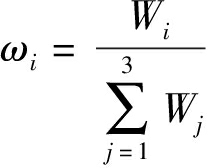
(58)
式中 Wi——第i个指标信息量
ωi——第i个指标权重
经计算可得,工作空间指标Vr权重为0.477;传递性综合指标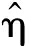G权重为0.319;灵巧度综合指标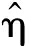Jm权重为0.204。
为实现多维指标的合理比较与筛选,采用基于TOPSIS法的Pareto前沿法处理上述性能指标。首先,将归一化后的Pareto前沿点分别代入
(59)
(60)
得到与正理想解的距离DM和与负理想解的距离Dm。
综合评分计算公式为
(61)
将DM和Dm代入到式(61),得到该解的综合评分,评分越高,越符合所需要求。
考虑到实际工程设计所需性能偏好不同,在客观赋权的基础上引入主观赋权。从不同偏好面列举出4种情况以作参考,其权重分配如表5所示。
表5 工程设计偏好方案
Tab.5 Schemes with engineering decision preferences
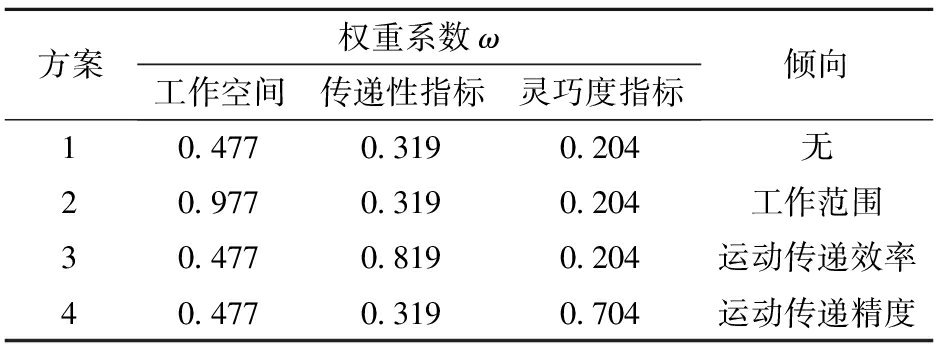
方案权重系数ω工作空间传递性指标灵巧度指标倾向10.4770.3190.204无20.9770.3190.204工作范围30.4770.8190.204运动传递效率40.4770.3190.704运动传递精度
其中,方案1采用上述权重客观赋权,表示三者无偏好。对应的,方案2偏好工作范围,方案3偏好传递效率,方案4偏好运动传递精度。方案设计结果如图15所示。
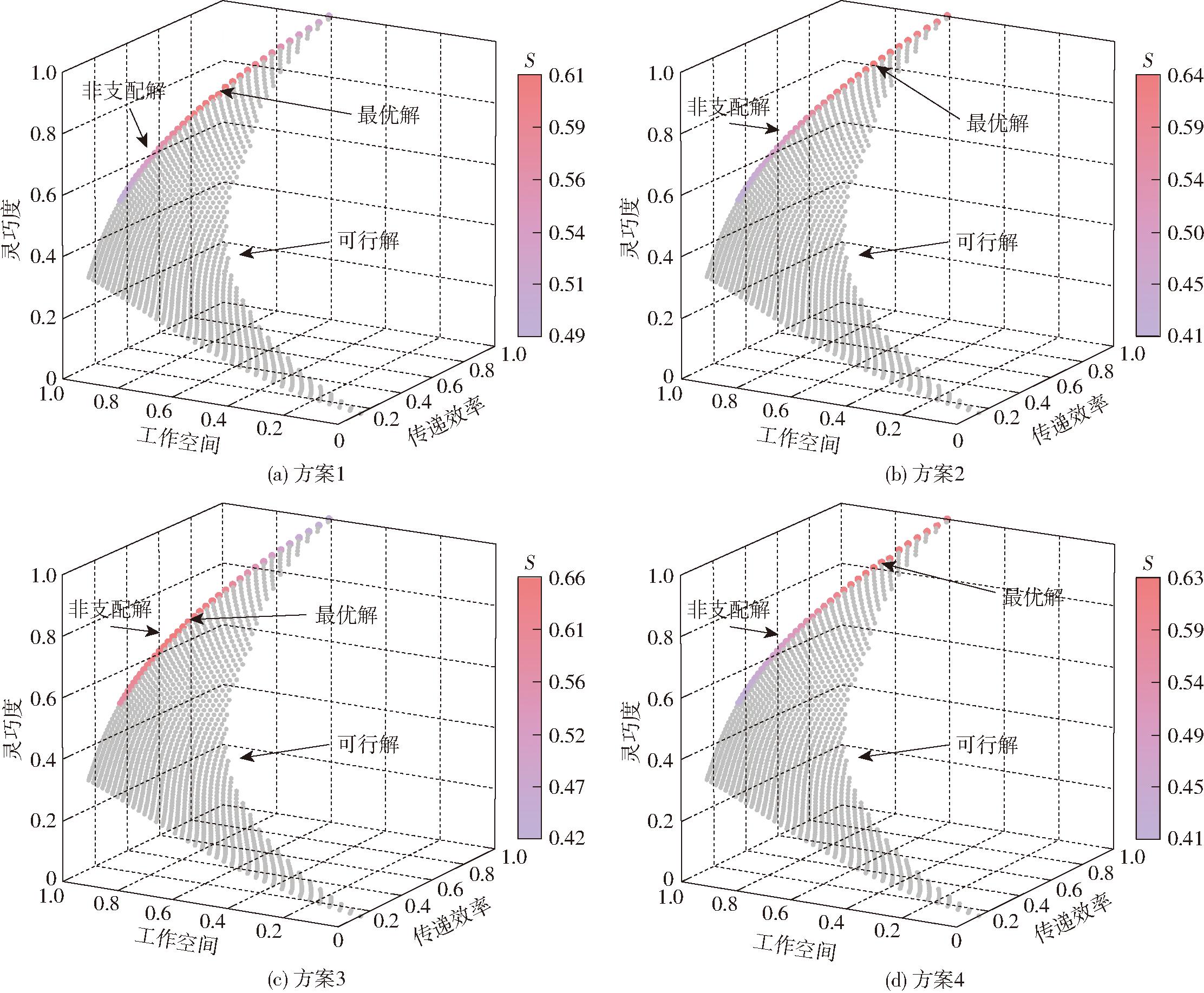
图15 各方案解集对应综合评分
Fig.15 Composite scores of schemes
根据样机预期设计尺寸,将静平台半径ra确定为0.160 m,则方案1～4对应的尺度设计和性能指标如表6所示。
表6 各方案对应的优化参数与性能指标
Tab.6 Optimized dimensions and indices of schemes
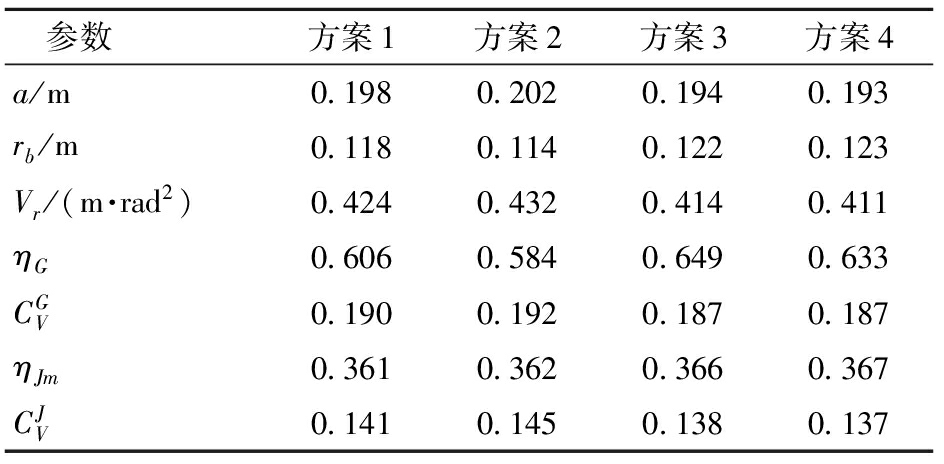
参数方案1方案2方案3方案4a/m0.1980.2020.1940.193rb/m0.1180.1140.1220.123Vr/(m·rad2)0.4240.4320.4140.411ηG0.6060.5840.6490.633CGV0.1900.1920.1870.187ηJm0.3610.3620.3660.367CJV0.1410.1450.1380.137
由图15与表6可知,混联机器人不同工程设计偏好对应的最优尺度参数不尽相同,其中,相比于均衡设计方案1,偏好设计方案2、3、4分别具有更加优异的工作范围、运动传递效率和运动传递精度。此外,多目标优化结果中运动/力传递性指标与其工作空间大小为负相关,与灵巧度指标为正相关。若在尺度设计过程中侧重工作范围提升,则其运动传递效率与运动精度偏低。反之,若侧重运动传递效率与精度,则会获得较小的机器人工作范围。这一结果再次表明,必须在混联机器人的尺度设计阶段综合考虑多目标均衡优化。因此,采用所提出的多目标均衡方法可以满足混联机器人不同的工程设计偏好,实现对应的最优尺度参数和性能指标,从而为设计者提供具有不同工程设计倾向的决策参考。
(1)通过对2PRU&1PRS-XY型混联机器人的运动学分析发现:其末端具有两转动三平动的5自由度运动能力,不存在约束奇异,并联模块无运动解耦性,混联机构整体具有部分运动解耦性。运动学性能指标在其工作空间内对称分布,可作为卧式5轴加工中心的骨架结构。
(2)定义了用于混联机器人全局性能评估的工作空间指标、传递稳定性指标和精度差异性指标,并在此基础上提出了一种基于多目标均衡优化思想的机器人尺度设计方法。该方法可从非劣解集中筛选出满足工程设计偏好的多目标均衡优化解。
(3)采用所提多目标均衡优化方法实现了2PRU&1PRS-XY型混联机器人主要尺度参数的优化设计,得到4种兼顾优化求解效率和多目标均衡需求的尺度参数设计方案。相比于无偏设计方案1,偏好设计方案2、3、4分别具有更加优异的工作范围、运动传递效率和运动传递精度,为设计者提供了具有不同工程设计倾向的多目标均衡决策参考。
[1] XIE Zenghui,XIE Fugui,LIU Xinjun,et al.Tracking error prediction informed motion control of a parallel machine tool for high-performance machining[J].International Journal of Machine Tools and Manufacture,2021,164:103714.
[2] NEUMANN K E.Robot:US,4732525[P].1988-03-22.
[3] NEUMANN K E.The key to aerospace automation[C]∥Proceedings of the SAE Aerospace Manufacturing and Automated Fastening Conference and Exhibition,2006.
[4] HENNES N.Ecospeed:an innovative machinery concept for high performance 5-axis machining of large structural components in aircraft engineering[C]∥3rd Chemnitz Parallel Kynematics Semiar,2002:763-774.
[5] 田昕,赵铁石,王唱,等.3-RHUR/PUS+PP混联机器人构型与性能分析[J].农业机械学报,2021,52(6):386-396.
TIAN Xin,ZHAO Tieshi,WANG Chang,et al.Configuration and performance analysis of 3-RHUR/PUS+PP hybrid robot[J].Transactions of the Chinese Society for Agricultural Machinery,2021,52(6):386-396.(in Chinese)
[6] 鹿玲,张东胜,许允斗,等.五自由度混联机器人尺度与结构优化设计[J].农业机械学报,2018,49(4):412-419.
LU Ling,ZHANG Dongsheng,XU Yundou,et al.Dimension and structure optimization design of 5-DOF hybrid manipulator[J].Transactions of the Chinese Society for Agricultural Machinery,2018,49(4):412-419.(in Chinese)
[7] 张俊,汤腾飞,方汉良,等.含过约束少自由度并联模块的混联机床:ZL201922126257.2[P].2020-02-11.
[8] ANGELES J.The design of isotropic manipulator architectures in the presence of redundancies[J].International Journal of Robotics Research,1992,11(3):196-201.
[9] 陈祥,谢富贵,刘辛军.并联机构中运动/力传递功率最大值的评价[J].机械工程学报,2014,50(3):1-9.
CHEN Xiang,XIE Fugui,LIU Xinjun.Evaluation of the maximum value of motion/force transmission power in parallel manipulators[J].Journal of Mechanical Engineering,2014,50(3):1-9.(in Chinese)
[10] LIU Xinjun,WU Chao,WANG Jinsong.A new index for the performance evaluation of parallel manipulators:a study on planar parallel manipulators[C]∥World Congress on Intelligent Control and Automation,2008:353-357.
[11] WANG Jinsong,WU Chao,LIU Xinjun.Performance evaluation of parallel manipulators:motion/force transmissibility and its index[J].Mechanism and Machine Theory,2010,45(10):1462-1476.
[12] 魏武,叶春台,袁银龙.基于群论的六足机器人运动空间研究[J].机器人,2016,38(5):522-530.
WEI Wu,YE Chuntai,YUAN Yinlong.Workspace analysis of a six-legged robot based on group theory[J].Robot,2016,38(5):522-530.(in Chinese)
[13] 冯李航,张为公,龚宗洋,等.Delta 系列并联机器人研究进展与现状[J].机器人,2014,36(3):375-384.
FENG Lihang,ZHANG Weigong,GONG Zongyang,et al.Developments of Delta-like parallel manipulators—a review[J].Robot,2014,36(3):375-384.(in Chinese)
[14] LIU Xinjun,WANG Jinsong.A new methodology for optimal kinematic design of parallel mechanisms[J].Mechanism and Machine Theory,2007,42(9):1210-1224.
[15] STOCK M,MILLER K.Optimal kinematic design of spatial parallel manipulators:application to linear Delta robot[J].Journal of Mechanical Design,2003,125(2):292-301.
[16] 马春生,尹晓秦,米文博,等.3-RPS并联机构基于任务空间的优化设计[J].制造技术与机床,2021,70(7):72-77.
MA Chunsheng,YIN Xiaoqin,MI Wenbo,et al.Optimal design of the 3-RPS parallel manipulator based on task based workspace[J].Manufacturing Technology &Machine Tool,2021,70(7):72-77.(in Chinese)
[17] 李研彪,郑航,徐梦茹,等.5-PSS/UPU并联机构的多目标性能参数优化[J].浙江大学学报(工学版),2019,53(4):654-663.
LI Yanbiao,ZHENG Hang,XU Mengru,et al.Multi-target parameters of performance optimization for 5-PSS/UPU parallel mechanism[J].Journal of Zhejiang University (Engineering Science),2019,53(4):654-663.(in Chinese)
[18] 刘晓飞,刘洋,何阳,等.2RPU+2UPR+RPR多冗余驱动并联机构运动学分析与优化[J].农业机械学报,2023,54(3):440-450.
LIU Xiaofei,LIU Yang,HE Yang,et al.Kinematic analysis and dimension optimization of multi-redundantly actuated parallel mechanism 2RPU+2UPR+RPR[J].Transactions of the Chinese Society for Agricultural Machinery,2023,54(3):440-450.(in Chinese)
[19] LEI Jingtao,WANG Jinhong.Orientation workspace analysis and parameter optimization of 3-RRPS parallel robot for pelvic fracture reduction[J].Journal of Mechanisms and Robotics,2023,15(5):051003.
[20] 王启明,张汉祖,蒋江月,等.平面平台型6-PSS并联机构构型选择与参数优化[J].农业机械学报,2022,53(5):449-458.
WANG Qiming,ZHANG Hanzu,JIANG Jiangyue,et al.Configuration selection and parameter optimization of 6-PSS parallel mechanism with planar platform[J].Transactions of the Chinese Society for Agricultural Machinery,2022,53(5):449-458.(in Chinese)
[21] 孙鹏,李研彪,张聪,等.基于运动性能分析的仿人机械臂尺度优化[J].中国机械工程,2022,33(19):2331-2340.
SUN Peng,LI Yanbiao,ZHANG Cong,et al.Scale optimization of humanoid robotic arms based on kinematic performance analysis[J].China Mechanical Engineering,2022,33(19):2331-2340.(in Chinese)
[22] MENG Qizhi,LIU Xinjun,XIE Fugui.Design and development of a Schönflies-motion parallel robot with articulated platforms and closed-loop passive limbs[J].Robotics and Computer-Integrated Manufacturing,2022,7:102352.
[23] XIE Fugui,LIU Xinjun,WANG Jinsong,et al.Kinematic optimization of a five degrees-of-freedom spatial parallel mechanism with large orientational workspace[J].Journal of Mechanisms and Robotics,2017,9(5):051005.
[24] DASTJERDI A H,SHEIKHI M M,MASOULEH M T.A complete analytical solution for the dimensional synthesis of 3-DOF Delta parallel robot for a prescribed workspace[J].Mechanism and Machine Theory,2020,153:103991.
[25] REN Jun,LI Qiliang,WU Hanhai,et al.Optimal design for 3-PSS flexible parallel micromanipulator based on kinematic and dynamic characteristics[J].Micromachines,2022,13(9):1457.
[26] HUANG Zhen,LI Qinchuan.Type synthesis of symmetrical lower-mobility parallel machanisms using the constraint-synthesis method[J].International Journal of Robotics Research,2003,22(1):59-79.
[27] 沈惠平,李菊,王振,等.基于结构降耦和运动解耦的并联机构拓扑结构优化及其性能改善[J].机械工程学报,2017,53(19):176-186.
SHEN Huiping,LI Ju,WANG Zhen,et al.Topology structure optimization and performance improvement for parallel mechanisms based on structure coupling-reducing and motion decoupling[J].Journal of Mechanical Engineering,2017,53(19):176-186.(in Chinese)
[28] TANG T,ZHAO Y,ZHANG J,et al.Conceptual design and workspace analysis of an exechon-inspired parallel kinematic machine[M]∥Advances in Reconfigurable Mechanisms and Robots Ⅱ.Springer International Publishing,2016:445-453.