我国是用水大国,农业用水占到总用水量的60%以上[1],“十四五”期间,我国进入发展新阶段,全面践行“节水优先”的治水方针、开展节水工作显得格外重要[2]。然而,目前我国灌溉用水的生产效率和利用率水平仍较低[3-5],因此大力研发低成本、高性能、便于推广的量水设备对灌区量水工作具有重要意义。
传统量水槽根据喉道长短和有无喉段可分为短喉道、长喉道和无喉道量水槽[6]。短喉道量水槽测流精度高但其结构复杂、施工困难,且需要水渠提供足够的水头[7];长喉道量水槽喉道相对较窄长,确保在喉道段中有稳定的临界水深,但是我国农田灌溉用水的含沙量较高,狭长喉道容易导致泥沙淤积,从而影响测流精度[8];无喉道量水槽由SKOGERBOE等[9]在巴歇尔量水槽的基础上优化改进而来,其结构简单、施工容易、抗泥沙作用强并且测流精度已有一定保障,目前在国外已有广泛应用。为了更好适应灌区的发展,国内外研究者陆续提出了不同外形轮廓的新型量水槽,实际上根据喉道长短,也属于短喉道、长喉道和无喉道量水槽的一种[10]。HAGER[11]将圆柱形量水柱放置于渠道中轴线并收缩水流,以此发明了圆柱形量水槽;王智等[12]对比V形和U形喉口形状的量水槽提出了U形渠道平底抛物线形量水槽;张志昌等[13]结合陕西灌区实际,通过缩窄喉道研制了直壁式量水槽;王玉宝等[14]借鉴多种量水槽设计了板柱结合型量水槽;为解决中国灌区量水存在的问题,吕宏兴等[15]参考机翼曲线,提出了机翼形量水槽。此后,贺梦杨等[16]简化了机翼曲线并由此提出仿翼形量水槽,刘鸿涛等[17]基于仿生技术优化机翼形量水槽得到仿鸽翼形量水槽,二者均具有良好的工作性能,初步证明了通过仿生、优化等手段寻找具有较高性能量水槽的可行性。
随着研究的深入,计算流体力学(Computational fluid dynamics,CFD)方法由于能实现流场可视化并节省人力物力,广泛用于量水槽流场分析。众多研究者基于CFD理论,对不同渠道断面下的圆柱形、抛物线形、直壁式、机翼形水槽进行模拟探究[18-21],得到不同工况下的量水槽水力特性,与试验结果基本一致,表明数值模拟方法精度较高,可用于灌区量水研究。与此同时,随着神经网络和优化算法的逐步发展,马舜等[22]基于叶素动量理论(Blade element momentum theory,BEM),通过CFD方法研究叶片的几何特性,对水轮机叶片性能进行优化,并验证了数字模型的可行性;王威等[23]将改进的NSGA-Ⅱ(Nondominated sorting genetic algorithm Ⅱ)遗传算法和CFD方法结合用于翼型减阻设计,提升了翼型的启动性能;孙斌等[24]基于多岛遗传算法(Multi-island genetic algorithm,MIGA)和CFD方法,以收阻比和淹没度为目标对机翼形建筑物进行了优化,提出了优化机翼形线形。总之,CFD方法效率高、成本低,能够和各种遗传算法相结合,已广泛用于量水设备的研究和优化。
在寻找水力性能较优且适用于量水槽设计的新型线形过程中,国内外众多学者对提升潜水器的性能已进行了深入研究[25-28],而潜水器在运动过程中受到的阻力情况和量水槽在灌区渠道中的受阻状态有一定的相似之处,可借鉴潜水器领域的研究成果,将其结构特点运用于量水槽体型设计。因此,本文基于潜水器的曲线结构设计量水槽线型方案,同时结合CFD方法和遗传算法进行多目标寻优,以得到最优线型个体,并通过物理模型试验对量水槽的各项水力性能进行分析。
常用于水下航行器设计的流线型有Myring形、卡克斯形和水滴形等[29-31],其中Myring形在潜水器领域的应用较为广泛,曾被用于Remus、Maya等著名潜水器。
Myring流线型应用于潜水器时,首尾段沿用其流线型主体,中间段为平行结构。由于我国部分灌区泥沙含量较高,本文拟选用不易淤堵的无喉道形式,故运用在量水槽体型设计时将流线型中段长度设为0,只分析首尾部曲线,其形状曲线方程为:
首部曲线方程
(1)
尾部曲线方程
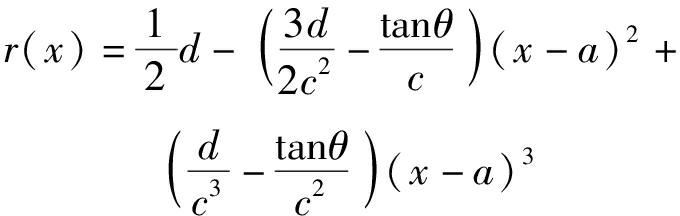
(2)
式中 a——收缩段长度,cm
c——扩散段长度,cm
x——曲线长轴上点到首部顶点的距离,cm
d——量水槽最大厚度的1/2,cm
n——收缩段锐度因子
θ——扩散段离去角,(°)
目前将Myring流线型形式应用在量水槽设计中的研究几乎没有,因此为了寻找水力性能最好的线形,通过改变曲线方程中的参数来调整收缩段和扩散段的饱和程度(图1)。量水槽最大厚度的变化将引起收缩比的变化从而影响其水力性能,故外形重构时固定量水槽最大厚度2d,仅选取收缩段长度a、收缩段锐度因子n、扩散段长度c和扩散段离去角θ作为优化的变量。

图1 不同n和θ时Myring方程所对应的线形
Fig.1 Different line shapes corresponding to Myring equation
最优拉丁超立方设计(Optimal Latin hypercube design)是拉丁超立方设计的改进版,通过优化采样点的位置,使得它们之间的距离最大化,从而更好地覆盖参数空间[32]。该方法可以提高采样效率,减少采样点数量,同时仍能保持良好的代表性和均匀性。因此本文拟采用最优拉丁超立方设计数值仿真方案,后续结合数值模拟平台,获得不同组合下线形的水力参数。
CFD方法凭借其低成本、高效率的特点得到广泛应用,众多研究表明了CFD方法建立三维量水槽模型进行分析的可行性。王蒙等[33]通过FLOW-3D软件对仿翼形量水槽进行数值模拟分析,发现实际和模拟结果流态变化基本一致,各项水力参数差距不大,水深和测流计算的平均误差分别为2.14%和2.37%,均控制在5%以内。因此本文采用FLOW-3D作为数值模拟软件。
渠道中的水流运动可采用Navier-Stokes方程描述,包括连续性方程和动量方程。
连续性方程为
(3)
动量方程为
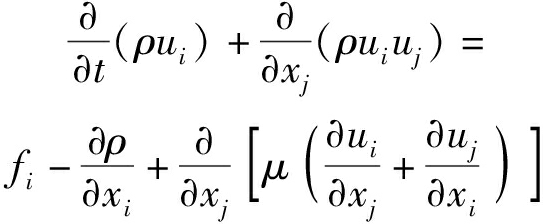
(4)
式中 xi、xj——空间坐标分量
ui、uj——流速矢量在对应方向上的分量,m/s
ρ——流体密度,kg/m3
t——流动时间,s
fi——质量力在各方向上的分力,N
μ——流体动力粘度,Pa·s
RNG k-ε模型是RNG(Renormalization group)理论与k-ε模型的结合,其旨在提高模拟的准确性和可靠性,在复杂的湍流模型中体现了较好的性能[34],RNG k-ε模型运输方程形式为:
湍动能方程
![]()
Gk+Gb-ρε-Ym+Sk
(5)
湍动能耗散率方程
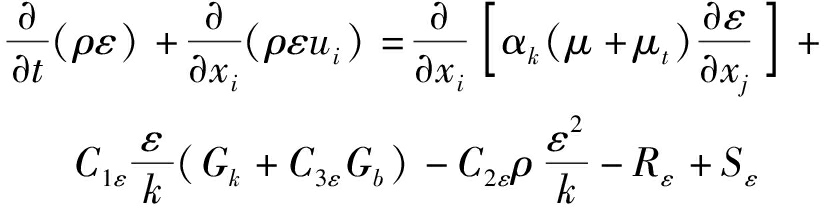
(6)
其中![]()
(7)
式中 Gk——平均速度梯度引起的湍流动能产生项
Gb——浮力产生的湍流动能产生项
Ym——可压缩湍流中波动膨胀对总耗散率的贡献
μt——流体湍动粘度,Pa·s
Rε——不同佛汝德数情况下的修正项
αk、αε——k和ε有效普朗特数的倒数
Sk、Sε——用户定义的源项
C1ε、C2ε、C3ε、Cu——常数系数
矩形模型渠道尺寸为10 m(长)×0.7 m(宽)×0.4 m(高),表面粗糙系数取0.011,量水槽进口距渠道进水口5 m;由于水流在流经量水槽时受到扰动,流态发生了较大的变化,因此对量水槽附近(量水槽进口上游0.1 m至出口下游0.13 m)的网格进行局部加密。坐标原点位于进水口右下角,x轴正方向为水流运动方向,y轴正方向指向渠道左壁,z轴正方向为重力加速度反方向。边界条件见图2,渠道上游进口设为流量进口边界,下游出口设为水流出口边界,渠道边壁和底部设为固壁边界,渠道顶部设为对称边界,网格区域的连接面设为网格叠加边界。
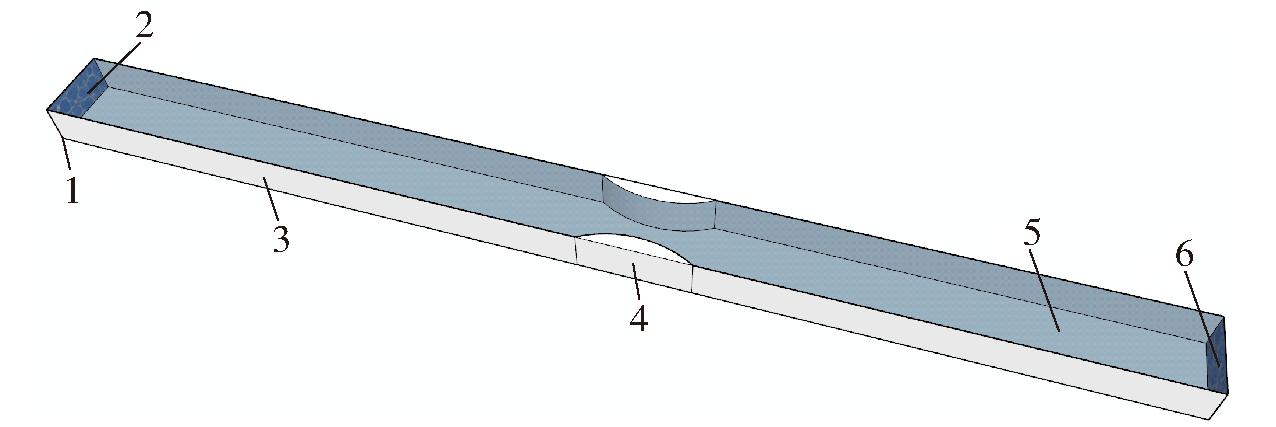
图2 模型及边界条件示例
Fig.2 Examples of models and boundary conditions
1.坐标原点 2.上游进口(流量进口) 3.渠道边壁(固壁) 4.量水槽 5.渠道底部(固壁) 6.下游出口(水流出口)
根据工程实际情况取设计流量为30 L/s,量水槽收缩比为0.60;量水槽局部水头损失表示水流流经时受到的阻力,水头损失百分比指水头损失占上游总水头百分比,可较好表示量水槽水力性能,而上游佛汝德数则可用于衡量量水槽上游段水流的平稳程度;基于众多学者在Myring流线型研究领域提出的可行域[25-28],结合量水槽实际应用的情况,参数取值范围见表1;采用最优拉丁超立方设计的40组方案进行数值模拟,结果如表2所示。
表1 流线型参数取值范围
Tab.1 Value range of flow profile parameters
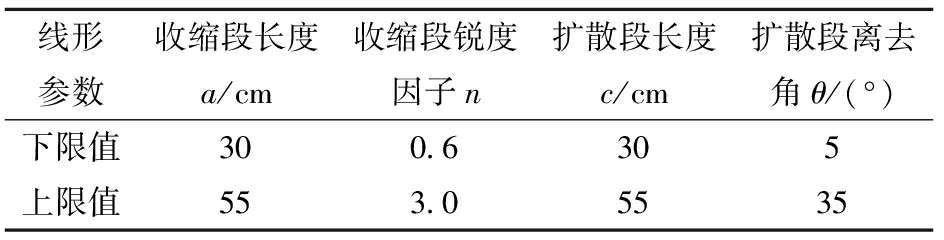
线形参数收缩段长度a/cm收缩段锐度因子n扩散段长度c/cm扩散段离去角θ/(°)下限值300.6305上限值553.05535
表2 最优拉丁超立方设计方案与水力性能
Tab.2 Optimal Latin hypercube design and hydraulic performance

方案序号收缩段长度a/cm收缩段锐度因子n扩散段长度c/cm扩散段离去角θ/(°)模拟水头损失百分比/%模拟上游佛汝德数146.62.3732.426.5012.350.391238.52.9043.36.8412.540.329336.42.6631.85.3014.420.335452.20.9244.923.9217.350.323540.10.7140.224.8214.460.329634.00.6441.333.4015.840.339751.31.9741.010.9912.720.334842.61.7848.422.6715.440.326941.32.1046.218.4916.810.3301047.21.3931.034.8813.720.3431147.82.0237.920.5414.860.3391248.32.8634.916.7915.740.3311340.02.5151.920.9016.770.3271441.01.4946.49.7514.020.3081536.81.5450.827.1115.060.3371645.02.7438.529.3014.990.3301733.31.6536.512.5313.000.3271839.11.8047.428.0315.200.3291950.61.1250.38.3112.430.3262035.11.1754.99.2213.190.3352142.22.8048.831.5014.580.3312249.71.5647.713.3914.130.3342335.91.8842.628.6112.920.3312449.22.5245.632.6412.810.3192550.52.2230.219.1214.350.3252644.52.1053.729.9012.770.3282733.52.9839.515.8212.530.3152852.91.3135.57.7617.170.3522934.72.3332.812.1515.430.3323049.00.8936.933.7314.680.3363137.40.8352.011.1415.500.3313241.71.0749.917.2315.530.3703338.21.2142.019.8715.140.3263444.11.3533.522.1416.340.3313546.21.0152.915.3115.280.3613643.22.4333.831.0514.170.3283745.71.6853.823.7412.120.3233837.92.1939.16.0813.600.3293951.52.5935.725.7513.330.3334044.00.7344.214.4714.400.348
RBF(Radial basis function)神经网络是一种前馈型神经网络,其具有结构简单、学习速度快、逼近性能优良和泛化能力强等特点,因此广泛运用于函数逼近、时间序列预测等领域[35]。模型决定系数R2和测试样本平均绝对百分比误差M可分别表示模型拟合精度和泛化能力;R2越接近1,拟合精度越高,M越小,泛化能力越强。
由于壅水高度和水头损失与流线型参数之间的关系无法用准确的数学模型定义,为了提高优化的准确性,本文以流线型量水槽收缩段长度a、收缩段锐度因子n、扩散段长度c和扩散段离去角θ为输入值,以水头损失百分比和上游佛汝德数为输出值,采用RBF神经网络拟合二者之间的映射关系,总样本为40组,其中训练样本35组、测试样本5组。训练得到的神经网络模型性能良好:水头损失百分比、上游佛汝德数与对应数值模拟数据的R2分别为 0.989 16和 0.999 78,表明模型精度较高,能够很好地表示线型参数和水力性能之间的复杂关系;测试样本水头损失百分比、上游佛汝德数的M分别为4.22%和2.88%,表明预测模型具有较高的精度和泛化能力。
NSGA-Ⅱ遗传算法是一种多目标优化算法,由DEB等[36]在NSGA的基础上改进非支配排序、拥挤度距离计算和引入精英策略进化而来,在处理多目标优化问题时具有良好的效果和性能。
本文的计算以最小水头损失百分比和上游佛汝德数为目标,流线型特征参数为约束条件,将训练好的神经网络作为适应度模型嵌入遗传算法中,通过非支配排序、计算拥挤度距离、交叉变异和精英策略等步骤,展开对线型参数的寻优计算。选取原始种群数为100,交叉遗传概率为0.9,变异概率为0.1,最大迭代次数为500,迭代完成后得到的Pareto前沿如图3所示,最优解分布呈下凹状,整体分布较均匀、连续性强,同时随着水头损失的减小,上游佛汝德数增大。
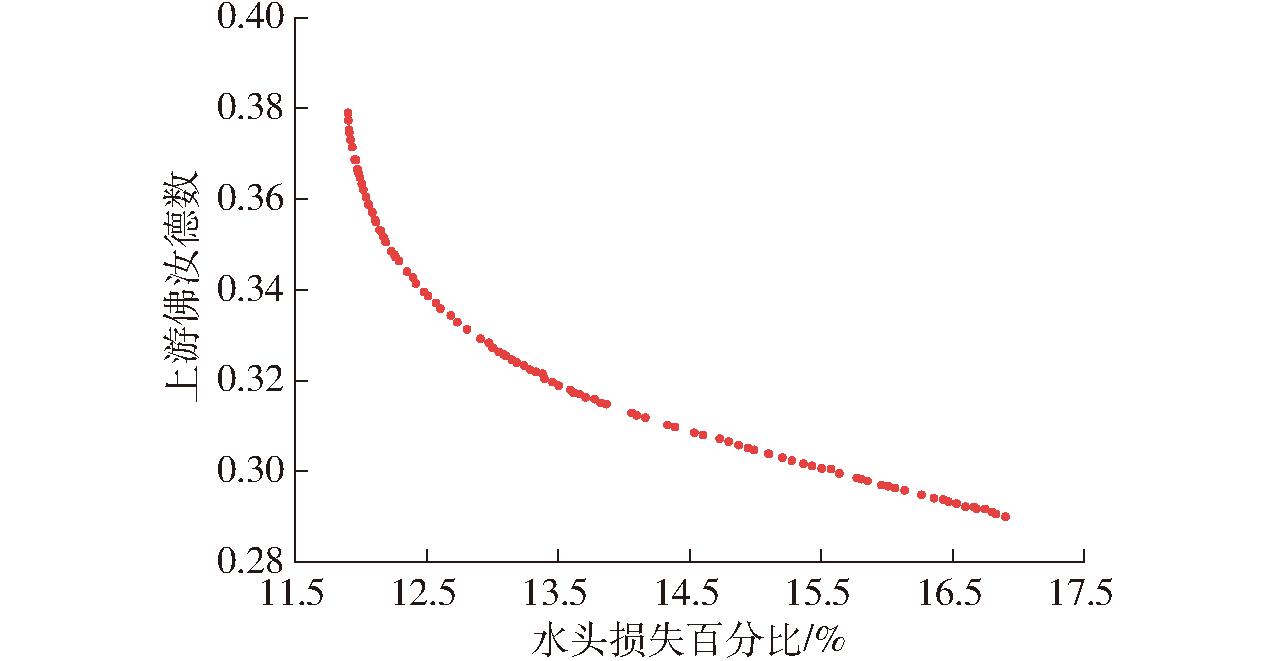
图3 基于遗传算法的最优前沿分布
Fig.3 Optimal frontier distribution based on genetic algorithm
TOPSIS(Technique for order preference by similarity to ideal solution)法通常被称为优劣解距离法,是一种常用的多属性决策方法,其原理为将决策矩阵中的所有方案与正理想解C1和负理想解C2的距离进行比较,既靠近C1且又靠近C2的方案即为最优方案,该方法适合对Patero最优解进行排序[37]。
由图3可知,两个目标函数相互制约,无法同时达到最优;而针对本文的两个目标函数而言,无法直接比较Patero最优解之间的优劣关系,因此利用TOPSIS法进行排序和评价,筛选出最优解,此时线型参数和对应的水头损失百分比以及上游佛汝德数见表3。
表3 最优方案参数和其对应的水头损失与上游佛汝德数
Tab.3 Optimal scheme parameters and their corresponding head loss and upstream Froude number

参数及对应水力性能收缩段长度a/cm收缩段锐度因子n扩散段长度c/cm扩散段离去角θ/(°)预测水头损失百分比/%预测上游佛汝德数数值45.90.7449.214.6313.000.327
为验证最优个体在不同渠道中的适应性,在不同断面类型、不同规模的渠道中进行数值模拟,分析各工况下量水槽的水力性能。在原矩形渠道的基础上,增加U形渠道[13]和梯形渠道[32];矩形渠道各参数的设定已在前文说明,梯形和U形渠道的各参数与矩形渠道保持一致。此外,根据对四川省升钟灌区南充干渠渠首的研究[38],选取一段顺直矩形渠道,渠道长75 m、宽4 m、高6 m,量水槽放置于距进口35 m位置,其余参数设定同前。
得到最优个体在矩形渠道中水头损失百分比为13.20%,上游佛汝德数为0.342,模拟结果和预测结果偏差分别为1.51%和3.80%,验证了混合算法的可行性;而在梯形和U形渠道中水头损失百分比、上游佛汝德数分别为12.84%、0.357和13.65%、0.339,与矩形渠道之间的差距均不超过10%。
各渠道流线和流速分布见图4,分布规律整体上较为相似:上游段流线相对顺直,在进入量水槽段后,渠道中轴线附近的水流受量水槽束窄作用较小,流向基本不变,而靠近侧壁的水流则先向渠道中部集中,后向两侧扩散,并在接触渠道边壁后与流速较慢的水流分离,形成低速涡流区;流速和流速矢量的分布和流线特征基本对应,流速在量水槽扩散段达到最大,在出口下游边壁附近水流存在横向分速度,和边壁摩擦从而使流速减缓。

图4 不同渠道下最优个体的流线和流速分布
Fig.4 Flow line and velocity distributions of optimal individuals in different channels
不同断面类型的渠道在灌区应用时各有优劣,不同规模的渠道也有其实际使用范围,在此不做讨论;但经分析发现,最优个体在各渠道中水流均较为平稳,过流顺畅,流线和流速分布规律基本一致,且水力性能差距不大,体现了Myring流线型量水槽在各类渠道中良好的适应性。
为了更好地分析Myring流线型量水槽的性能,进行物理模型试验。试验于西北农林科技大学水力学大厅进行,使用的试验矩形钢槽长17 m、宽0.7 m,渠道为平坡;通过遥控装置设定流量并用电磁流量计加以监测,误差±1%;水深通过SCM60型测针测量,精度0.1 mm。
研究不同收缩比量水槽的性能,故在不破坏优化结果的前提下,对收缩比为0.60的量水槽进行等比例缩放,从而改变量水槽的收缩比。物理模型试验在数值模拟(0.60)基础上加设收缩比0.50、0.54、0.58、0.62、0.66,共计6组收缩比,在数值模拟(30 L/s)基础上加设流量20、25、35、40、45、50、55、60 L/s,共计9组流量。
4.2.1 水头损失百分比
在自由出流时不同收缩比下水头损失百分比与流量的关系如图5所示。水头损失百分比为8.19%~19.04%,总体上来看水头损失百分比随着流量和收缩比的增大而减小,且流量变化带来的影响显著弱于收缩比的影响。收缩比大于等于0.58时水头损失较小,为8.19%~15.85%,同时收缩比为0.62和0.66时水头损失分布更集中,说明该情况下水头损失受流量影响更小,可作为较优的收缩比范围。
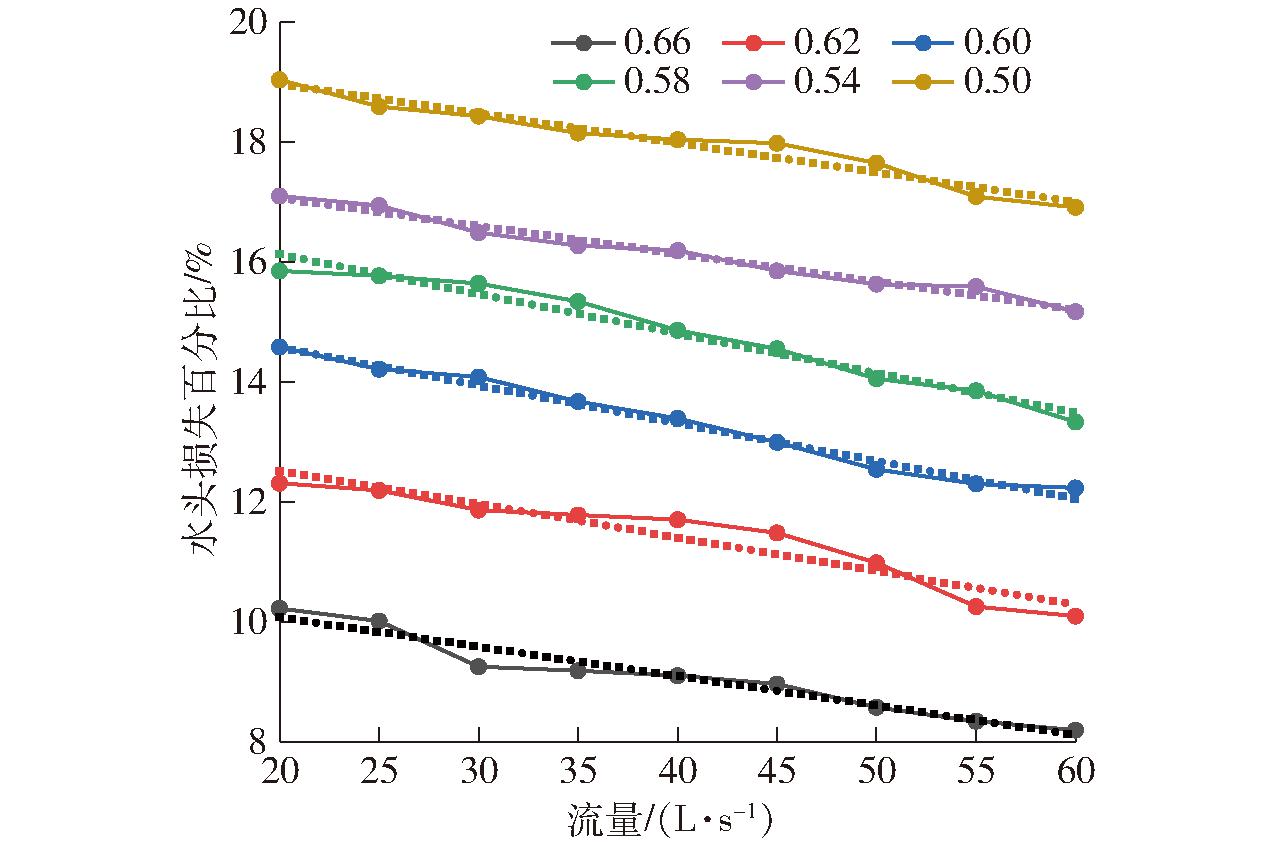
图5 不同收缩比下水头损失百分比和流量的关系曲线
Fig.5 Relationship curves between percentage of head loss and flow rate under different contraction ratios
4.2.2 上游佛汝德数
不同收缩比下上游佛汝德数与流量的关系如图6所示。由图6可知,各工况上游佛汝德数范围为0.26~0.42,均满足灌区量水规范规定小于0.50的标准。但收缩比为0.66时上游佛汝德数最大值已大于0.40,而收缩比为0.50时上游佛汝德数随流量的变化幅度较大,因此实际布置时应尽量避免收缩比过大或过小。
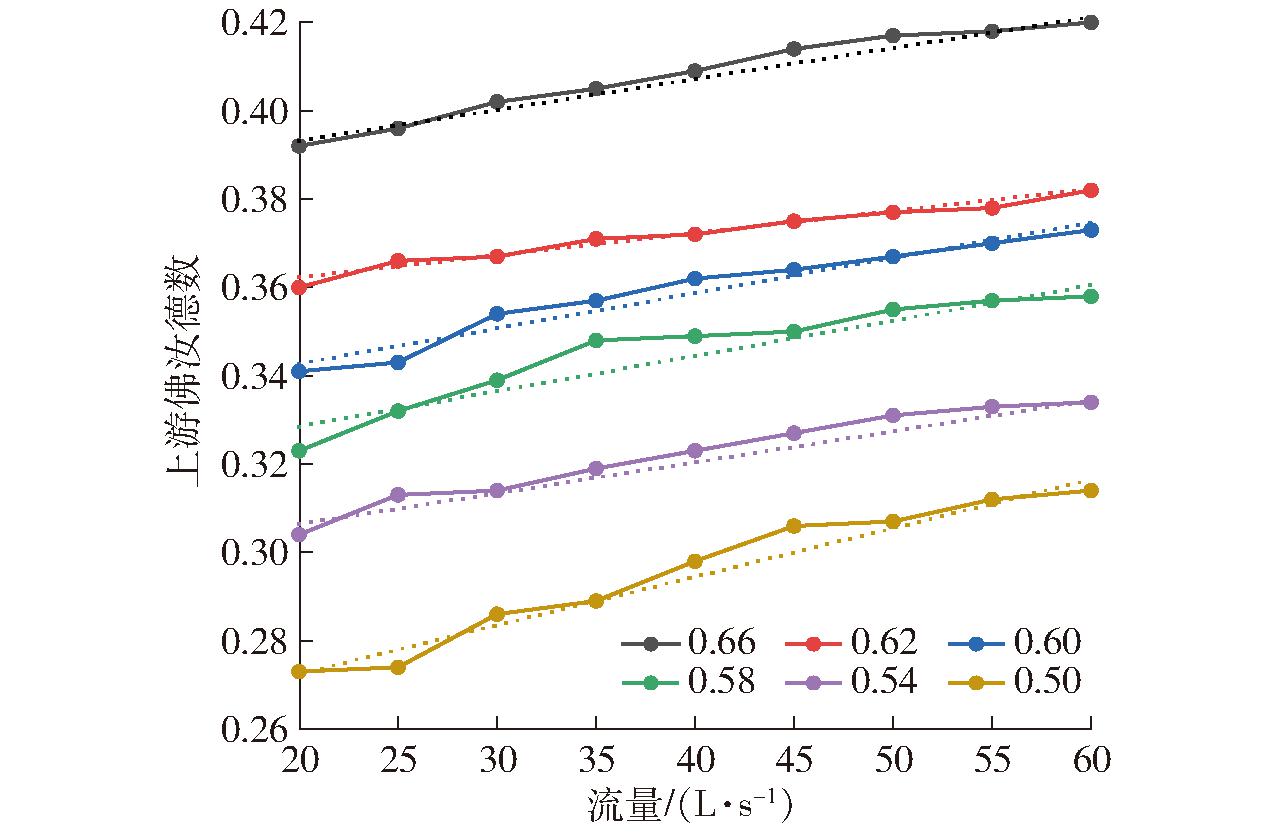
图6 不同收缩比下上游佛汝德数和流量的关系曲线
Fig.6 Relationship curves between upstream Froude number and flow rate under different contraction ratios
4.2.3 壅水高度
不同收缩比下壅水高度和流量的关系如图7所示。壅水高度随着流量的增大而增大,而随着收缩比的增大而减小。在所有工况下上游壅水高度最小值为1.11 cm、最大值为4.06 cm,由图7可以看出,收缩比为0.50及0.54时,壅水高度较高,且随流量的增大趋势相对较大,因此实际布置时建议收缩比大于等于0.58。
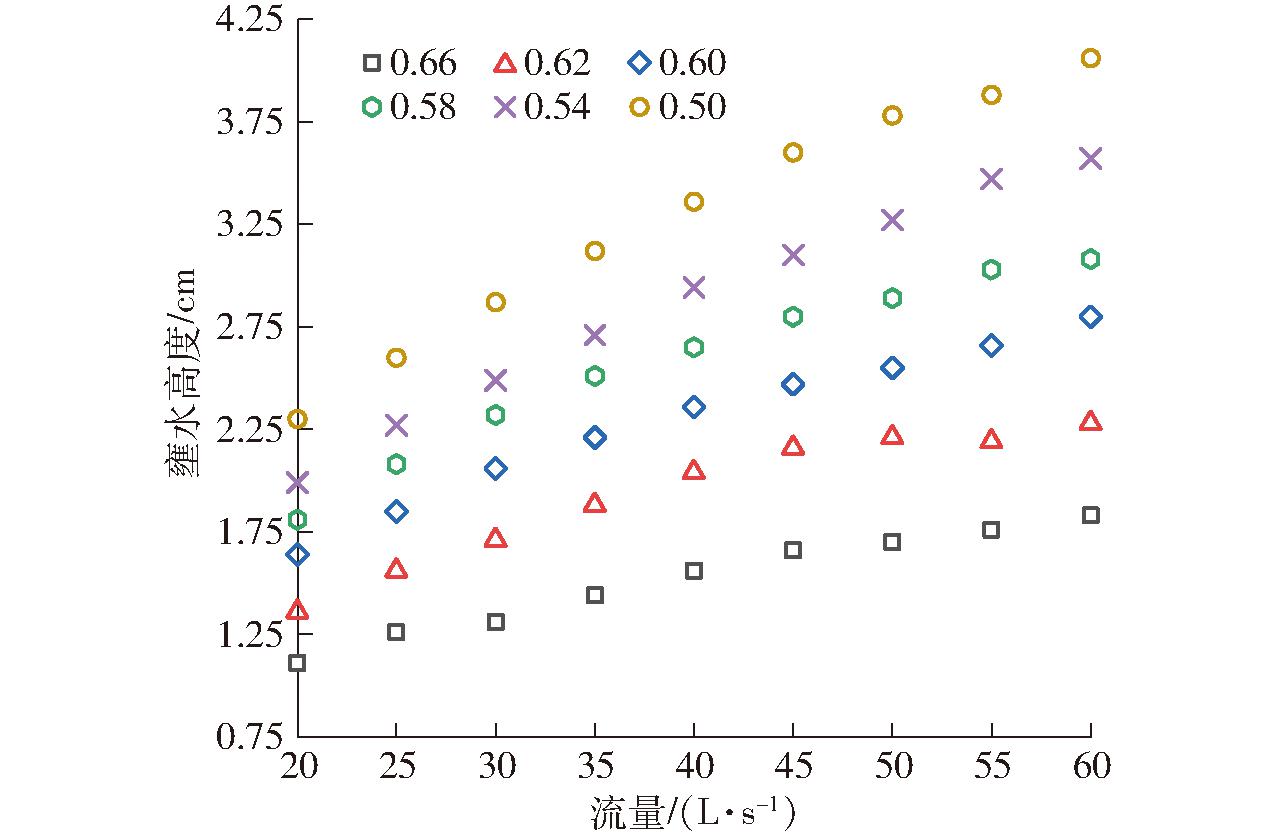
图7 不同收缩比下壅水高度和流量的关系曲线
Fig.7 Relationship curves between damming height and flow rate under different contraction ratios
4.2.4 临界淹没度
通过调节下游尾水闸门控制下游水位直至影响上游水位,得到不同收缩比下临界淹没度与流量的关系,如图8所示,临界淹没度范围为0.778~0.890,均值为0.834;临界淹没度随着收缩比的增大而增大,表明收缩比更大的量水槽具有更大的测流范围,收缩比为0.58~0.66时临界淹没度均大于0.80,因此在实际布置时建议收缩比为0.58~0.66。
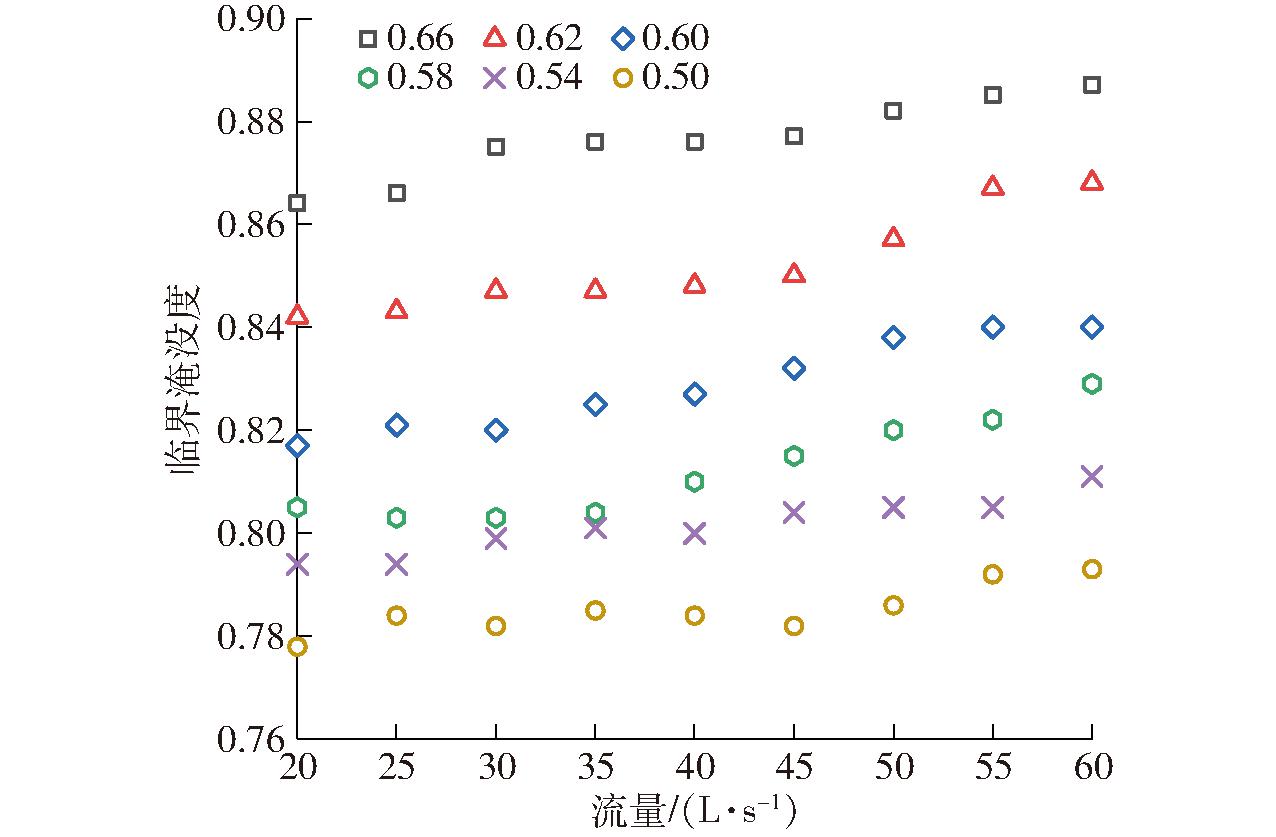
图8 不同收缩比下临界淹没度和流量的关系
Fig.8 Relationship between critical submergence and flow rate under different contraction ratios
在渠道中安装量水槽后,水流流经收缩段时流态由缓流转变为急流,槽内出现临界流断面,而临界流水深和流量之间存在稳定的函数关系,这就是量水槽的测流原理。结合试验数据,采用量纲分析原理,得到Myring流线型量水槽在矩形渠道中的测流公式为
(8)
式中 Q——通过量水槽的流量计算值,m3/s
g——重力加速度,m/s2
Bc——喉口断面宽度,m
h1——上游水深,m
Myring流线型量水槽实测流量和计算流量对比如表4所示,测流范围内最大相对误差为3.49%,最小相对误差为0.36%,平均相对误差为2.09%,表明Myring流线型量水槽具有测流精度高的优点,可在灌区渠道中投入使用。
表4 实测流量与计算流量对比
Tab.4 Comparison between measured and calculated flows

收缩比实测流量/(L·s-1)计算流量/(L·s-1)相对误差/%收缩比实测流量/(L·s-1)计算流量/(L·s-1)相对误差/%收缩比实测流量/(L·s-1)计算流量/(L·s-1)相对误差/%0.5021.4922.14-3.0127.9728.77-2.8532.8333.91-3.3035.5736.81-3.4940.6941.90-2.9747.5148.31-1.6853.5254.61-2.0457.7159.66-3.3864.9765.97-1.540.5420.1920.64-2.2525.6125.98-1.4631.8532.13-0.8936.6737.90-3.3540.3141.07-1.8948.5149.59-2.2454.2355.34-2.0460.7761.54-1.2666.5768.09-2.280.5819.9820.19-1.0425.0325.51-1.9231.0130.860.4935.0735.99-2.6340.5541.95-3.4646.5748.14-3.3752.2353.62-2.6658.4159.79-2.3763.8165.93-3.330.6019.1519.35-1.0424.9325.13-0.8130.1130.000.3635.3335.70-1.0640.0741.24-2.9246.2347.13-1.9451.4352.87-2.8057.1758.59-2.4963.2164.37-1.840.6219.0518.602.3624.1123.811.2530.0529.432.0635.1334.960.4840.1740.85-1.6945.5846.50-2.0251.2252.42-2.3357.1358.57-2.5363.0764.03-1.520.6618.0517.562.7122.8922.611.2128.3327.602.5633.7732.872.6539.2138.172.6644.1343.172.1749.7348.572.3455.0354.241.4360.1159.860.42
(1)将Myring流线型应用于量水槽研究,采用拉丁超立方设计方法构建了以收缩段长度、收缩段锐度因子、扩散段长度和扩散段离去角为参数,量水槽水头损失百分比和渠道上游佛汝德数为目标函数的数值模拟方案,基于数值模拟平台建立了基础数据集。利用基础数据集训练RBF神经网络,得到模型的水头损失百分比、上游佛汝德数R2分别为0.989 16和0.999 78,M分别为4.22%和2.88%,表明训练完成的神经网络具有较高的性能。
(2)将神经网络作为NSGA-Ⅱ遗传算法的适应度模型得到Pareto前沿解,再通过TOPSIS方法得到最优个体。当收缩段长度为45.9 cm、锐度因子为0.74,扩散段长度为49.2 cm、离去角为14.63°时,水头损失百分比预测值和仿真模拟值分别为13.00%和13.20%,相对误差为1.51%,上游佛汝德数预测值和仿真模拟值分别为0.327和0.342,相对误差为3.80%。结果表明最优个体在各种渠道中的水头损失和上游佛汝德数表现均较好,且均具有流线分布均匀、过流顺畅的特点。
(3)通过矩形渠道模型试验,发现收缩比为0.58~0.66时量水槽具有较小的壅水高度、水头损失和较大的临界淹没度;各工况下量水槽具有较高的测流精度(最大相对误差为3.49%,最小相对误差为0.36%,平均相对误差为2.09%),同时上游佛汝德数均小于0.5,二者测流均满足灌区量水规范要求。Myring流线型量水槽作为新型量水槽的一种,综合性能较好,在灌区渠道中具有广阔的应用前景。
[1] 尚松浩,蒋磊,杨雨亭.基于遥感的农业用水效率评价方法研究进展[J].农业机械学报,2015,46(10):81-92.
SHANG Songhao,JIANG Lei,YANG Yuting.Review of remote sensing-based assessment method for irrigation and crop water use efficiency[J].Transactions of the Chinese Society for Agricultural Machinery,2015,46(10):81-92.(in Chinese)
[2] 王清义.对新时代做好水利教育工作的认识和思考[J].中国水利,2019(12):7-8.
WANG Qingyi.Observations and recommendations on water education in the new era[J].China Water Resources,2019(12):7-8.(in Chinese)
[3] 马涛,刘九夫,彭安帮,等.中国非常规水资源开发利用进展[J].水科学进展,2020,31(6):960-969.
MA Tao,LIU Jiufu,PENG Anbang,et al.Progress in development and utilization of non-conventional water resources in China[J].Advances in Water Science,2020,31(6):960-969.(in Chinese)
[4] 邓铭江,陶汪海,王全九,等.西北现代生态灌区建设理论与技术保障体系构建[J].农业机械学报,2022,53(8):1-13.
DENG Mingjiang,TAO Wanghai,WANG Quanjiu,et al.Theory and technical guarantee system construction of modern ecological irrigation district in northwest China[J].Transactions of the Chinese Society for Agricultural Machinery,2022,53(8):1-13.(in Chinese)
[5] 郭萍,潘琦,岳琼,等.基于2型模糊集的多目标农业-生态水土资源优化配置[J].农业机械学报,2022,53(12):353-365.
GUO Ping,PAN Qi,YUE Qiong,et al.Multi-objective modelling for optimal allocation of agricultural-ecological water and land resources based on type-2 fuzzy sets[J].Transactions of the Chinese Society for Agricultural Machinery,2022,53(12):353-365.(in Chinese)
[6] 潘志宝,吕宏兴,魏溪.灌区量水槽的应用研究现状与进展[J].西北农林科技大学学报(自然科学版),2007,35(4):213-217.
PAN Zhibao,LÜ Hongxing,WEI Xi.Current applied research and advances of measuring flume in irrigation district[J].Journal of Northwest A&F University(Natural Science Edition),2007,35(4):213-217.(in Chinese)
[7] 王长德.我国灌溉量水技术的应用[J].中国水利,2005(7):26-28,34.
WANG Changde.The technology applied to irrigation water measurement in China[J].China Water Resources,2005(7):26-28,34.(in Chinese)
[8] CASTRO-ORGAZ O,MATEOS L.Water discharge measurement in agricultural catchments using critical depth flumes affected by sediment deposition[J].Journal of Irrigation and Drainage Engineering,2014,140(3):04013018.
[9] SKOGERBOE G V,HYATT M L,ENGLAND J D,et al.Measuring water with Parshall flumes[R].USA:Utah Water Research Laboratory,1966:1-49.
[10] 徐义军,韩启彪.我国灌区量水槽研究概述[J].节水灌溉,2012(5):56-59.
XU Yijun,HAN Qibiao.Summary of current research on measuring flume in irrigation districts of China[J].Water Saving Irrigation,2012(5):56-59.(in Chinese)
[11] HAGER W H.Modified venturi channel[J].Journal of Irrigation and Drainage Engineering,1985,111(1):19-35.
[12] 王智,朱凤书,刘晓明.平底抛物线形无喉段量水槽试验研究[J].水利学报,1994,25(7):12-23.
WANG Zhi,ZHU Fengshu,LIU Xiaoming.Experimental study on flat parobolic throatless flume for flow measurement[J].Journal of Hydraulic Engineering,1994,25(7):12-23.(in Chinese)
[13] 张志昌,张宗孝,闫晋垣,等.一种新型的量水设备——U形渠道直壁槽式量水堰[J].西安理工大学学报,1992,8(1):44-52,70.
ZHANG Zhichang,ZHANG Zongxiao,YAN Jinyuan,et al.A new type of flow measuring equipment—straight wall trough measuring weir of the U-shaped channel[J].Journal of Xi’an University of Technology,1992,8(1):44-52,70.(in Chinese)
[14] 王玉宝,杨娟,李鑫,等.U形渠道便携式板柱结合型量水槽水力性能研究[J].农业机械学报,2019,50(6):332-330.
WANG Yubao,YANG Juan,LI Xin,et al.Hydraulic performance of plate-column portable flume in U-shaped channel[J].Transactions of the Chinese Society for Agricultural Machinery,2019,50(6):332-330.(in Chinese)
[15] 吕宏兴,刘焕芳,朱晓群,等.机翼形量水槽的试验研究[J].农业工程学报,2006,22(9):119-123.
LÜ Hongxing,LIU Huanfang,ZHU Xiaoqun,et al.Experimental research on airfoil-shaped flow flume[J].Transactions of the CSAE,2006,22(9):119-123.(in Chinese)
[16] 贺梦杨,尚海鑫,张宽地,等.仿机翼形便携式量水槽水力特性试验与数值模拟[J].农业工程学报,2021,37(12):117-124.
HE Mengyang,SHANG Haixin,ZHANG Kuandi,et al.Hydraulic performance experiments and numerical simulation of portable water measuring flume of imitating airfoil shape[J].Transactions of the CSAE,2021,37(12):117-124.(in Chinese)
[17] 刘鸿涛,屈忠义,李怡阳,等.基于贝叶斯网络理论与仿生技术的翼形量水槽优化[J].工程科学与技术,2022,54(6):105-115.
LIU Hongtao,QU Zhongyi,LI Yiyang,et al.Optimization of wing-shaped measuring flume based on Bayesian network theory and bionic technology[J].Advanced Engineering Sciences,2022,54(6):105-115.(in Chinese)
[18] 吉庆丰,袁晓渊,葛蕴,等.梯形渠道圆柱形量水槽水力特性数值模拟[J].灌溉排水学报,2012,31(2):59-61.
JI Qingfeng,YUAN Xiaoyuan,GE Yun,et al.Numerical simulation research on hydraulic characteristics of cylinder measuring flume in trapezoidal channel[J].Journal of Irrigation and Drainage,2012,31(2):59-61.(in Chinese)
[19] 郝晶晶,马孝义,王波雷,等.基于VOF的量水槽流场数值模拟[J].灌溉排水学报,2008,27(2):26-29.
HAO Jingjing,MA Xiaoyi,WANG Bolei,et al.Numerical simulation of flow field in flow-measuring flume based on VOF method[J].Journal of Irrigation and Drainage,2008,27(2):26-29.(in Chinese)
[20] 牟献友,李超,李国佳,等.U形渠道直壁式量水槽水力特性数值模拟[J].华北水利水电大学学报(自然科学版),2010,31(2):16-19.
MOU Xianyou,LI Chao,LI Guojia,et al.Research on hydraulic characteristics numerical simulation of U-shaped channel straight wall measuring flume[J].Journal of North China Institute of Water Conservancy and Hydroelectric Power(Natural Science Edition),2010,31(2):16-19.(in Chinese)
[21] 孙斌,吕宏兴,潘志宝.矩形农渠机翼形量水槽水力特性数值模拟[J].干旱地区农业研究,2010,28(2):155-158.
SUN Bin,LÜ Hongxing,PAN Zhibao.Numerical simulation of hydraulic characteristics on the airfoil-shaped measuring-flume in rectangular canal[J].Agricultural Research in the Arid Areas,2010,28(2):155-158.(in Chinese)
[22] 马舜,李伟,刘宏伟,等.水平轴潮流能发电系统能量捕获机构研究[J].机械工程学报,2010,46(18):150-156.
MA Shun,LI Wei,LIU Hongwei,et al.Research on the energy capture device of horizontal axis tidal current energy conversion systems[J].Journal of Mechanical Engineering,2010,46(18):150-156.(in Chinese)
[23] 王威,王军,杨伟刚,等.基于熵产方法的跨音速翼型减阻优化设计[J].华中科技大学学报(自然科学版),2018,46(2):1-6.
WANG Wei,WANG Jun,YANG Weigang,et al.Entropy generation method for aerodynamic optimization design of transonic airfoil to drag minimization[J].Journal of Huazhong University of Science and Technology (Natural Science Edition),2018,46(2):1-6.(in Chinese)
[24] 孙斌,吕宏兴,宋晨光,等.基于Hicks-Henne型函数和MIGA的机翼形建筑物多目标水力优化[J].四川大学学报(工程科学版),2013,45(4):13-20.
SUN Bin,LÜ Hongxing,SONG Chenguang,et al.Multi-objective optimization of airfoil-shaped hydraulic structure based on Hicks-Henne shaped function and MIGA[J].Journal of Sichuan University (Engineering Science Edition),2013,45(4):13-20.(in Chinese)
[25] 姜钧喆.水下滑翔机总体设计与水动力性能分析[D].上海:上海交通大学,2020.
JIANG Junzhe.Design and hydrodynamic analysis of underwater glider[D].Shanghai:Shanghai Jiao Tong University,2020.(in Chinese)
[26] 戴鹏.基于参数化的三体组合式自主水下航行器多目标优化设计研究[D].广州:华南理工大学,2020.
DAI Peng.Research on multi-objective optimal design of three-body combined autonomous underwater vehicle based on parameterization[D].Guangzhou:South China University of Technology,2020.(in Chinese)
[27] 苗怡然.基于参数化的水下航行器主体结构设计优化研究[D].哈尔滨:哈尔滨工程大学,2018.
MIAO Yiran.Parameterization optimization of autonomous underwater vehicle main structure[D].Harbin:Harbin Engineering University,2018.(in Chinese)
[28] 李阳,吴俊飞,熊学军.仿生翼水下航行器直航运动时水动力性能分析[J].机械制造,2020,58(8):35-39,57.
LI Yang,WU Junfei,XIONG Xuejun.Hydrodynamic performance analysis of underwater vehicle with bionic tail during straight ahead motion[J].Machinery,2020,58(8):35-39,57.(in Chinese)
[29] MYRING D F.A theoretical study of body drag in subcritical axisymmetric flow[J].Aeronautical Quarterly,1976,27(3):186-194.
[30] 杜月中,闵健,郭字洲.流线型回转体外形设计综述与线型拟合[J].声学技术,2004(2):93-97,101.
DU Yuezhong,MIN Jian,GUO Zizhou.A review and mathematical formulation of shape design of streamlined bodies of revolution[J].Technical Acoustics,2004(2):93-97,101.(in Chinese)
[31] WU Baoshan,PAN Ziying,XIA Xian,et al.Investigation of the hdrodynamic caracteristics of body of revolution with stern ring-wing[J].Journal of Ship Mechanics,2003(6):54-59.
[32] LIEFVENDAHL M,STOCKI R.A study on algorithms for optimization of Latin hypercubes[J].Journal of Statistical Planning &Inference,2006,136(9):3231-3247.
[33] 王蒙,张宽地,王文娥,等.用于梯形渠道的仿翼形便携式量水槽水力性能[J].农业工程学报,2023,39(3):76-83.
WANG Meng,ZHANG Kuandi,WANG Wene,et al.Hydraulic performance of portable flow measuring flume of imitating aerofoil in the trapezoidal channel[J].Transactions of the CSAE,2023,39(3):76-83.(in Chinese)
[34] 周招,王均星,梁砚,等.深尾水消力池非完全宽尾墩消能试验研究[J].水科学进展,2017,28(5):729-737.
ZHOU Zhao,WANG Junxing,LIANG Yan,et al.Study on incompletely flaring gate pier energy dissipation in deep tail water stilling basin[J].Advances in Water Science,2017,28(5):729-737.(in Chinese)
[35] LLANAS B,SAINZ F J.Constructive approximate interpolation by neural networks[J].Journal of Computational and Applied Mathematics,2006,188(2):283-308.
[36] DEB K,PRATAP A,AGARWAL S,et al.A fast and elitist multiobjective genetic algorithm:NSGA-Ⅱ[J].IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.
[37] 刘强,俞国燕,梅端.基于Dynaform与RBF-NSGA-Ⅱ算法的冲压成形工艺参数多目标优化[J].塑性工程学报,2020,27(3):16-25.
LIU Qiang,YU Guoyan,MEI Duan.Multi-objective optimization of stamping forming process parameters based on Dynaform and RBF-NSGA-Ⅱ algorithm[J].Journal of Plasticity Engineering,2020,27(3):16-25 (in Chinese)
[38] 苏华英.灌区量水槽试验与数值模拟研究[D].成都:四川大学,2006.
SU Huaying.Experiment and numerical simulation of measuring flume of irrigation area[D].Chengdu:Sichuan University,2006.(in Chinese)