OSID：
中国秸秆资源丰富,2020年秸秆资源总量达8.56×108 t[1]。秸秆捡拾致密成型机将田间秸秆收集并挤压成型为秸秆颗粒,成为推进秸秆综合利用的重要途径。成型机主轴转速根据料仓内秸秆量进行调控,转速与秸秆喂入量相匹配,可避免料仓内秸秆量过多而堵塞成型机,有利于提高成型机田间作业的效率。
随着农业机械向智能化方向发展,对农机装备的检测与控制成为研究热点,目前研究主要集中在喂入量、挤压力以及转速控制[2-3]等方面。王伟等[4]建立了移动式秸秆致密成型机田间秸秆喂入量的变论域模糊PID速度调控系统,实现秸秆喂入量的精准调控。王韦韦等[5]依托模糊PID算法及PLC控制器实现对固定式生物质机组粉料喂入量的控制。谭睿[6]建立了玉米秸秆固化成型试验平台,采用应变片方式完成环模挤压力的测量。牛峰等[7]针对电机参数失配导致的转速运行不稳定问题,提出了一种模型预测转速控制系统,探索了模型参数失配对电机转速稳定性的影响规律。苗小利等[8]针对白噪声下PID控制引起的转速输出波动问题,提出模糊WMR-PID控制方法,该方法具备优异的控制性能与鲁棒性能。CHOI等[9]针对电机转速控制策略出现的鲁棒性与抖振抑制问题,提出了基于鲸鱼优化算法的滑模控制方法,提高了转速跟踪性能。GAO等[10]针对电机转速易受电压误差影响问题,提出一种基于电压误差补偿的控制策略,提高了系统的稳定性。张国栋等[11]搭建实验平台探索了颗粒成型率最优组合方案。孙喜月[12]在保持含水率、粉碎程度、模具长度不变的情况下,探讨了成型机主轴转速在100～140 r/min变化时转速对颗粒成型的影响规律,主轴转速在120 r/min时,颗粒成型效果最好,秸秆表面无焦化现象。广义预测控制[13](Generalized predictive control,GPC) 广泛应用于转速控制系统中,主要包括预测模型[14]、滚动优化[15]、反馈校正[16]3个基本特征,GPC能有效减小控制模型突变和扰动产生的影响,若预测输出的数据丢失或预测输出依赖的数据量少时,GPC控制器性能难以保证。
合理的主轴转速决定致密成型机的生产效率,转速慢时,若成型机喂入量大,由于转速与喂入量不匹配,料仓内秸秆堆积过多,成型机易堵塞。秸秆颗粒的成型效率与转速、水分、喂入量等参数密切相关,转速作为重要的控制参数,对提高颗粒成型率有重要意义。为解决主轴转速的控制问题,提高秸秆捡拾致密成型机的作业效率,本文以辽宁宁越农机装备有限公司设计的560XG型秸秆捡拾致密成型机为研究对象,结合机、电、液、预测与迭代学习控制(Iterative learning control,ILC)等先进技术,建立一种新的转速控制方法,并通过场地收获试验与田间试验验证本算法的有效性、稳定性与正确性。
秸秆捡拾致密成型机集秸秆捡拾、粉碎、输送与颗粒压制于一体,如图1所示。成型机作业时秸秆由前端的捡拾与粉碎设备处理后,进入输送设备(螺旋输送器与输送筒),最后在料仓下部的成型装置中进行压块成型,液压装置控制成型装置的主轴转速,转速传感器对转速进行测量,其工作流程如图2所示。
图1 秸秆捡拾致密成型机实物图
Fig.1 Physical image of straw picking compactor
1.液压装置 2.转速传感器 3.出料口 4.成型装置
图2 成型机工作流程图
Fig.2 Workflow diagram of straw compactor
秸秆捡拾致密成型机转速控制系统由工控机(ZPC150-T112型,广州市崇畅计算机科技有限公司)、控制器(处理器为STM32F407VET6,意法半导体公司)、无级变速装置(EBG-03型,济南隆利液压装置有限公司)、转速传感器(SC12-20K型,南京凯基特传感科技有限公司)及成型装置主轴(560XG-48-ZZ01型,辽宁宁越农机装备有限公司)等组成,如图3所示。工控机显示屏提供人机操作界面,D/A转换模块将单片机控制器中的数字量信号转换为模拟量电压信号,对无级变速装置的伺服阀控设备进行控制,由无级变速装置驱动成型装置的主轴旋转,转速传感器对转速进行测量并反馈至控制系统。
图3 硬件系统结构图
Fig.3 Hardware system architecture diagram
泵控液压回路如图4所示,伺服控制机构由伺服阀、伺服缸、反馈杠杆及斜盘组成,采用力反馈式控制回路,通过控制伺服阀阀芯位移来控制活塞位移,进而改变变量泵斜盘的倾角,达到排量改变的目的,从而实现液压马达调速。补油泵使用单向阀向低压管道补油,补偿泄漏,保证管道压力。泵控液压油提供动力驱动液压马达,液压马达驱动压块成型装置主轴,主轴带动压辊进行秸秆物料的压块成型。
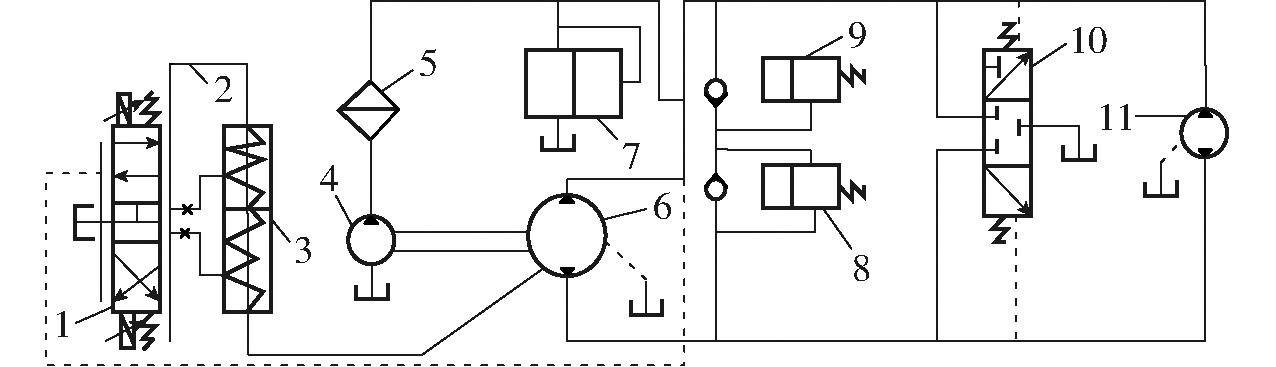
图4 泵控液压马达系统原理图
Fig.4 Schematic of pump controlled hydraulic motor system
1.伺服阀 2.反馈杠杆 3.变量液压缸 4.补油泵 5.过滤器 6.变量泵 7.低压安全阀 8.低压溢流阀 9.高压安全阀 10.梭阀 11.液压马达
在田间作业中,成型机通过自动调控系统实现稳定的秸秆喂入量,主轴转速需要与喂入量相匹配。转速具有非严格重复运行的特性,其控制可用迭代学习控制方法[17],迭代学习控制能产生较好的控制效果,将带参数模型辨识的GPC与ILC方法相结合,可避免依赖单一过程的预测输出模型,提高控制系统精度。主轴转速控制系统的原理图如图5所示,系统主要包括GPC-ILC控制器、驱动器、液压马达及转速传感器,其中驱动器包括比例放大器、电液伺服阀、液压缸、变量泵。GPC-ILC控制器根据设定转速n0与转速传感器测量值之间的偏差,通过驱动器对液压马达转速进行调节,其中比例放大器对GPC-ILC控制器输出的信号进行放大或缩小,调控电液伺服阀控制液压缸改变泵的排量。
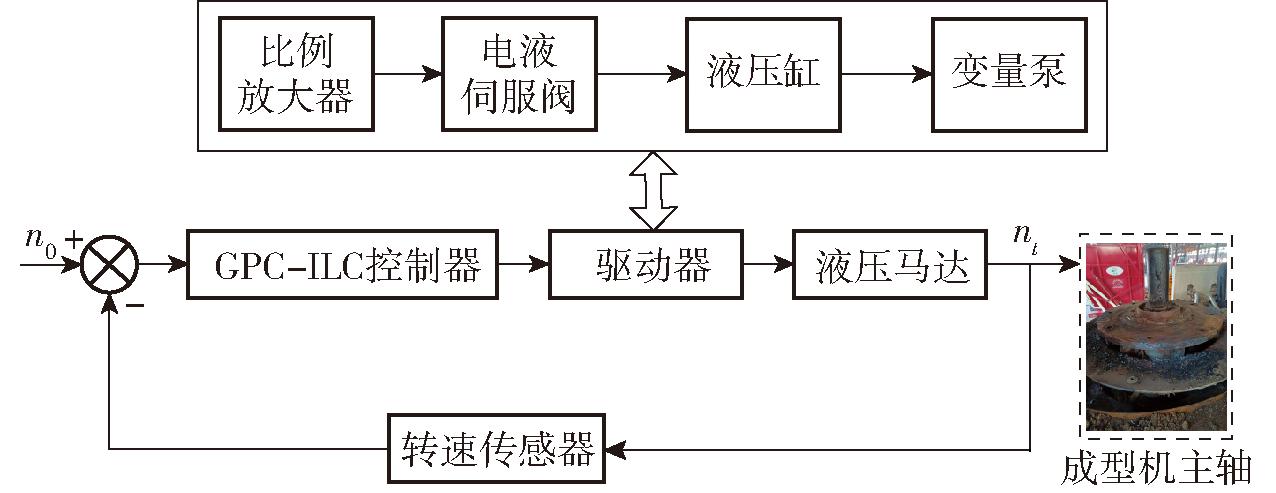
图5 转速控制系统原理图
Fig.5 Schematic of speed control system
泵控液压马达传递函数θ(s)为
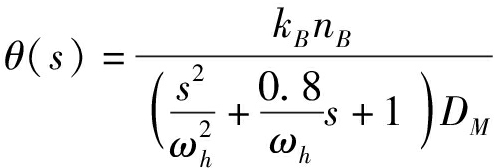
(1)
式中 DM——马达排量,m3/s
nB——泵转速,r/min
ωh——马达固有频率,rad/s
kB——比例系数
伺服阀传递函数Q(s)为
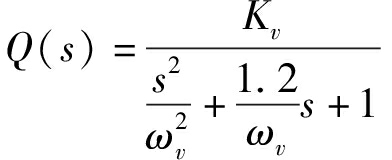
(2)
式中 Kv——伺服阀增益
ωv——伺服阀动态特性参数,rad/s
液压缸传递函数M(s)为
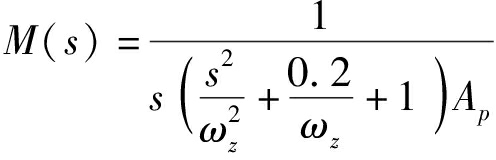
(3)
式中 Ap——液压缸面积,m2
ωz——液压缸固有频率,rad/s
依据说明书及相关经验,选取ωv=1 000 rad/s,Kv=6.55×10-3 m3/(s·A),DM=10-4 m3/s,ωh=5.4 rad/s,nB=1 452.2 r/min,ωz=2 000 rad/s,Ap=0.001 587 m2,电液控制系统传递函数G(s)为
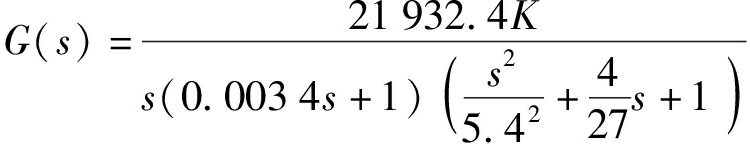
(4)
式中 K——比例放大器增益
本文转速控制模型选用易于在线辨识的带控制量的自回归积分滑动平均模型(CARIMA)[18],采用双线性变换将公式(4)离散化后得到
=
(5)
式中 z——后移算子
Y(z)——系统输出信号
U(z)——系统控制信号
将式(5)转换为CARIMA模型
y(k)-0.76y(k-1)+y(k-2)+
0.57y(k-3)+0.23y(k-4)=
28.3u(k)+113.2u(k-1)+
169.8u(k-2)+113.2u(k-3)+
(6)
其中
式中 ξ(k)——白噪声
Δ——差分算子
u(k)——控制量
y(k)——致密成型机转速
CARIMA模型表达式记为
(7)
其中
A(z-1)=1+a1z-1+a2z-2+…+anz-n
B(z-1)=b0+b1z-1+b2z-2+…+bmz-m
致密成型机田间作业时,模型参数有可能发生突变,造成模型失配,通过引入多步预测与控制增量的最小化性能函数,得到当前运行过程中未来时刻的控制序列,增强系统的稳定性,性能指标函数为
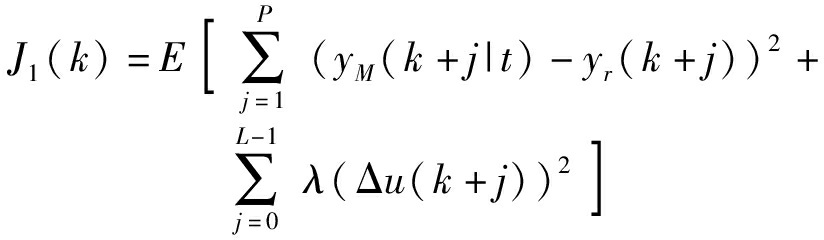
(8)
式中 E[·]——方差函数
L——控制步程
λ——控制增量加权系数
yr(k+j)——k+j时刻预测输出值
yM(k+j|t)——t时刻第j步向前预测输出值
P——控制时域
Δu(k+j)——相邻采样时刻控制变化量
引入并求解丢番图方程[19]后,求得预测模型k+j时刻的输出值为
(9)
其中
Y=[y(k+1) y(k+2) … y(k+N)]T
ΔU=[Δu(k) Δu(k+1) … Δu(k+M-1)]T
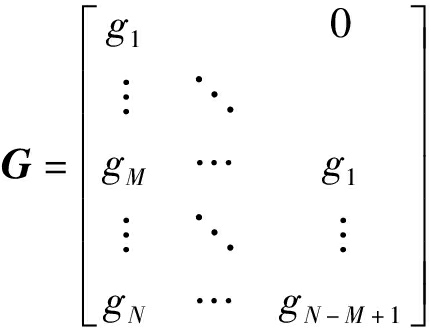
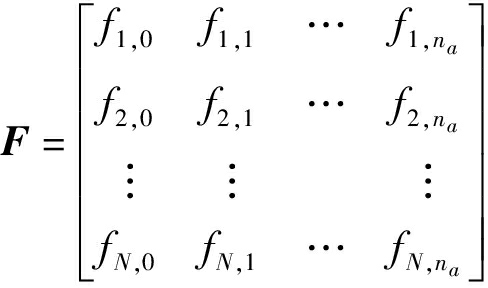
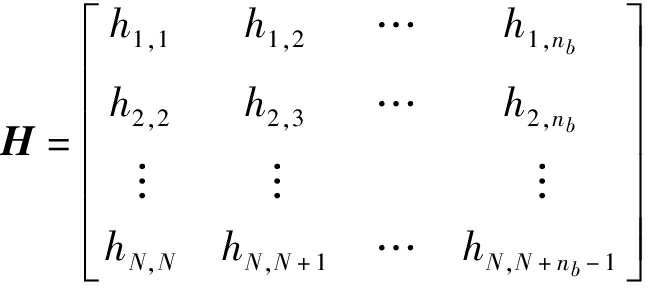
式中 na——多项式A(z-1)阶数
nb——多项式B(z-1)阶数
为使压块成型机主轴转速平滑过渡到设定值w,参考轨迹[20]形式为一阶平滑模型,其表达式为
(10)
式中 yr(t)——转速期望输出值
a——柔化系数,取0～1
y(t)——转速实际输出值
w——转速设定值
将公式(9)代入公式(8),性能指标函数对t方向变化量ΔU(t)求导,可得J1(k)最优解表达式
u(t)=u(t-1)+
(11)
式中 I、W——单位矩阵
在控制过程中,CARIMA对系统动态特性能进行粗略估计,为使CARIMA模型与主轴转速调节系统相匹配,实现转速调节系统优良特性,需不断根据实际输入输出信息在线修正模型参数,本文选用带遗忘因子的递推最小二乘法[21-22]对CARIMA模型进行反馈校正。
由公式(7)可得
Δy(k)=φT(k)θ+ε(k)
(12)
其中
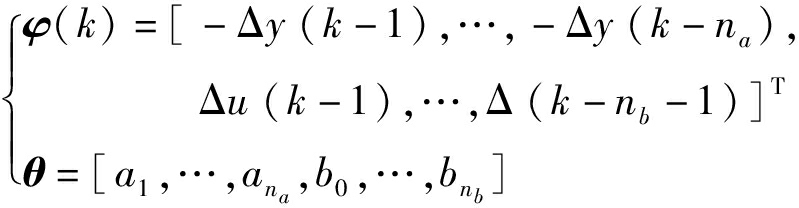
(13)
式中 ε(k)——不相关的随机序列
采用渐消记忆的递推最小二乘迭代公式估计参数向量
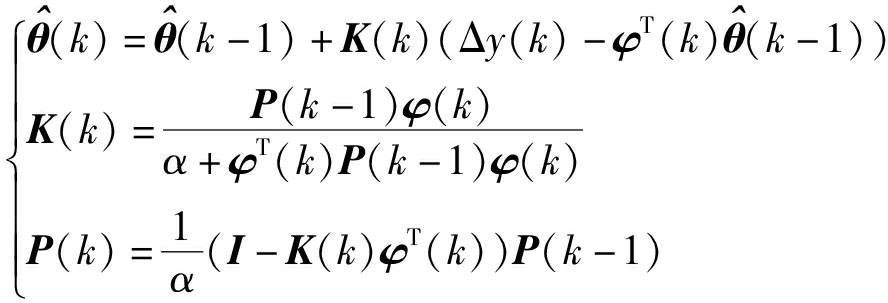
(14)
式中 α——遗忘因子,取0.8～1.0
K(k)——权因子
P(k)——正定的协方差矩阵
最小二乘递推法流程为:①输入模型的初始值,并设定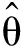
(0)、P(0)与α的初值。②采集当前输入输出信号:u(k)与y(k)。③利用式(14)计算K(k)、P(k)与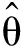(k)。④k值加1,转步骤②,继续循环。
迭代学习控制ILC[23-25]是一种新型的控制策略,反复应用先前的经验产生期望输出,减小控制误差,使系统输出收敛于期望值,提高控制精确度。ILC利用上一次的数据与误差,本质上是一种前馈控制算法[26-27]。ILC的目标是通过无限次迭代使偏差趋于0,本文引入最小二次型迭代学习控制的性能指标函数
(15)
式中 ek——迭代误差向量
Uk——迭代控制输入向量
‖·‖ M——取矩阵M范数
‖·‖ N——取矩阵N范数
假设对于线性系统L=L0+GU,期望轨迹为lr,存在期望控制向量Ur满足lr=lr0+GUr,式中,G为描述算子,L、L0、U分别为输出向量、输出向量初值、输入向量,lr0为期望轨迹值。
将期望轨迹值与预测输出值的跟踪误差表示为向量形式
ek=ek-1G(Uk-1-Uk)
(16)
由公式(15)、(16)可得
(17)
对输入变化向量ΔUk求一阶偏微分并令等式等于0,可得迭代控制律为
Uk=Uk-1+(GTMN+N)-1Mek-1
(18)
致密成型机田间作业压制颗粒时,主轴转速具有非严格重复性,为进一步提高控制系统的精度,在迭代控制过程的t时刻,用上一次迭代过程中的输入与输出数据得到最优预测值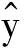
k(t),然后采用t时刻之前的累加平均误差修正预测值。第k次迭代过程t时刻的累加平均误差为
(19)
式中 
k(t)——第k次迭代过程t时刻的预测误差
修正后的预测值为
(20)
式中 β——误差校正因子,取0.1～1
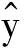(t)——修正后预测输出值
在作业过程中采集的转速由于机器振动等环境因素影响存在误差,在预测控制量不断校正过程中,使用累加平均进行校正,可降低数据问题对控制性能的影响。公式(20)中校正因子β采用误差分级策略,用m代表k(t)与
之比,当m为(0,3]、(3,5]、(5,7]、(7,9]、(9,10]时,β分别为0.1、0.3、0.6、0.8、1.0,误差校正分级策略有利于提升运算的速度,增加预测值的准确性。
基于GPC-ILC的成型机控制流程如图6所示,步骤为:
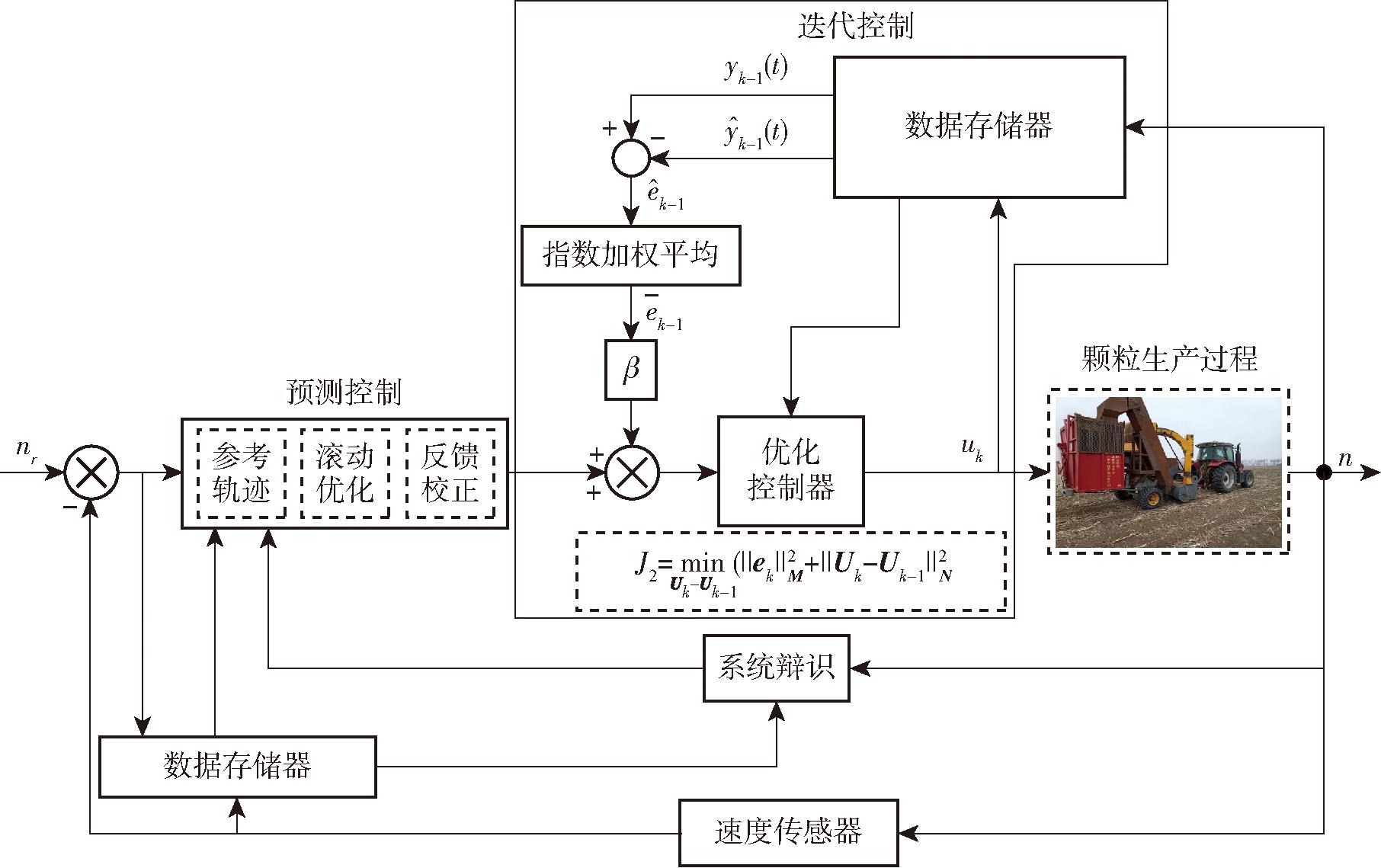
图6 基于GPC-ILC的成型机控制流程图
Fig.6 Control flowchart of forming machine based on GPC-ILC
(1)广义预测控制及迭代学习参数初始化(预测步长、控制步长、柔化因子等)并设定参考轨迹。
(2)在压块成型机工作的第k次迭代t时刻,其输出uk(t)作用于转速控制装置,得到系统输出yk(t)。
(3)根据k-1时刻的控制量uk-1与转速输出值yk-1(t)辩识系统的结构参数,得到系统的控制模型,求解丢番图方程得到预测控制模型的预测值。
(4)求取迭代过程中的预测误差并进行存储,利用累加平均法补偿预测值,得到校正预测值
(5) 
代入式(12)计算下一迭代过程输入uk+1(t)。
(6)若t<T(设定的采样总时间),t=t+1,返回步骤(2);若t=T,令k=k+1,返回步骤(1)。
以辽宁宁越农机装备有限公司560XG型致密成型机为研究对象,依据现场采集的主轴转速数据,采用本文提出的控制算法与GPC、PID算法进行仿真对比验证,验证本文算法的有效性,仿真试验环境处理器为Intel(R) Celeron(R) CPU 5205U @ 1.90 GHz,内存16 GB,操作系统为64位Windows 11,软件为Matlab2016a/Simulink。仿真参数选择:M=I(I为单位矩阵),N=0.06I,采样周期t=1 s,采样样本为1 000。
图7、8分别为不同控制算法下转速的跟踪对比效果与转速误差,本文方法取第10次迭代过程数据,可以得出:GPC-ILC算法相比于传统GPC算法与PID算法,有较好的控制效果与跟踪能力,所得转速控制曲线以较高精度满足致密成型机田间作业要求,传统算法在启动与制动环节存在较大跟踪误差,GPC-ILC算法、GPC算法与PID算法误差平均值分别为0.42、0.89、1.13 r/min。
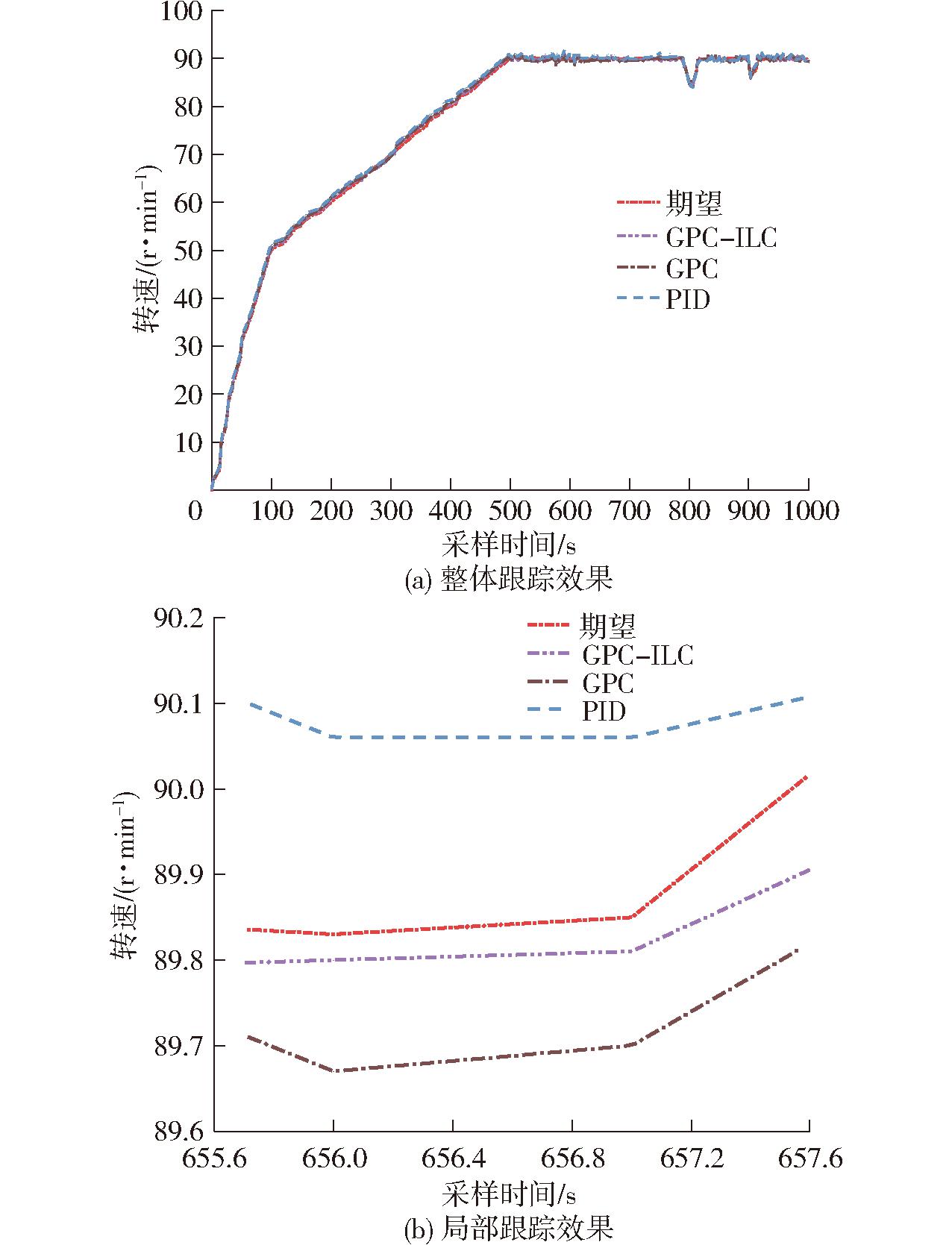
图7 转速跟踪曲线
Fig.7 Speed tracking curves
图8 转速误差曲线
Fig.8 Speed error curves
为验证系统的有效性,以560XG型移动式秸秆致密成型机为试验样机,于2023年3月1日在辽宁宁越农机装备有限公司进行转速调控试验与场地秸秆模拟收获制粒试验,于2023年3月4日在公司现代农业示范基地进行田间秸秆收获制粒试验。
试验设备包括:工控机,主控器,手持式转速测量仪(TA8146A型,特安斯电子公司),便携式计算机(逸15-15S型,安徽海擎信息科技公司),Jlink仿真器(V8型,SEGGER公司)。运行GPC-ILC算法的工控机,处理器为 Intel(R) Core(TM) i5-3337U CPU@1.80 GHz,64位Windows 10操作系统,内存16 GB,硬盘1 TB,工控机带有网络、USB、RS232 等工业处理接口,含有电容触摸功能。MCU 主控器,接收工控机控制信号并输出到执行端,时钟高达168 MHz,具备USART接口、模拟量输入与输出接口。工控机与主控制器硬件平台具有微秒级运算能力。
调控试验:工控机与主控制器采用RS232通讯接口进行通讯,在工控机调控软件上将不同的转速值写入主控制器,采用手持式转速测量仪对主轴实际转速进行测量,对比调控软件的显示值,判断控制系统对转速调控的有效性。
模拟收获试验:采用带有秸秆切碎装置的561-ZY型玉米联合收获机田间作业粉碎玉米秸秆(玉米品种为必祥199)后,秸秆自然晾晒,含水率为5%～10%,采用562-ZK型打捆机收集秸秆。储存15 d后破包进行模拟收获试验,3次铺设长方形秸秆,每块长为200 m,宽为2.0 m,分别采用GPC-ILC、GPC、PID算法。在3块长方形秸秆田中,每块前100 m单位面积秸秆质量为1 kg,后100 m单位面积秸秆质量为2 kg,密度一致,厚度均匀。压块成型机前端捡拾装置与螺旋输送器离地10 cm。模拟收获时,采用相同车速0.5 m/s,由于单位面积秸秆质量不同,在100 m处秸秆喂入量增加,达到主轴负荷增加的目的。在200 m收获结束时,成型装置正常工作,料仓的秸秆含量不断减少,实现主轴减负荷。
田间试验:致密成型机在田间不平整区域(长200 m,宽2 m)作业收获秸秆并制粒,车速调整为0.5 m/s,主轴转速调整为120 r/min,分析主轴转速在田间不平整情况下变化情况。
试验数据由主控制器上的内存卡进行存储与记录,通过数据的分析,可获取判断转速稳定性的指标:转速调整时间Ts、最大动态偏差L、余差D。转速调整时间Ts为转速从开始调整到完成所需时间。最大动态偏差L为转速偏离目标值的最大值。余差D是转速稳定值与其目标值之间的残余偏差,是衡量转速调控系统稳态准确性的指标。
转速调控试验如图9所示,通过工控机软件(图10)依次向主控制器写入主轴转速100、110、120、130 r/min,分别运转1 min,采用手持式转速测量仪对主轴转速进行测量并记录,手持式转速测量仪与工控机显示值如表1所示,控制误差小于1%,控制系统对转速的控制与监测满足精度要求。
表1 转速监测结果
Tab.1 Speed monitoring results
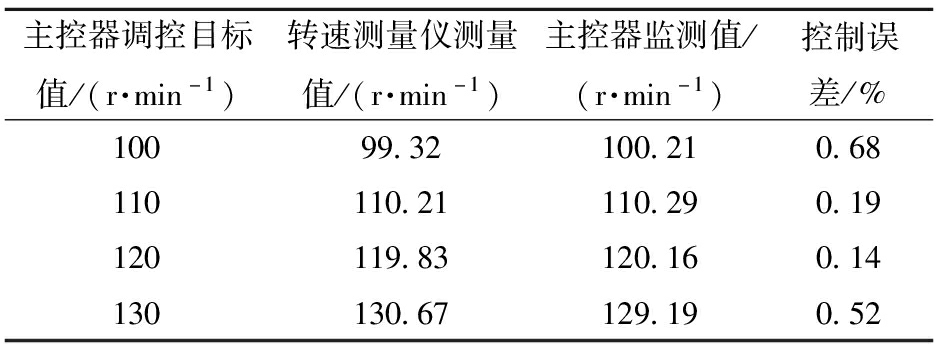
主控器调控目标值/(r·min-1)转速测量仪测量值/(r·min-1)主控器监测值/(r·min-1)控制误差/%10099.32100.210.68110110.21110.290.19120119.83120.160.14130130.67129.190.52
图9 转速调试试验
Fig.9 Speed debugging test
图10 软件界面
Fig.10 Software interface
如图11所示,试验前调整车速为0.5 m/s,通过屏幕先设定转速为120 r/min,进行秸秆收获,实现主轴增负荷试验,收获结束时通过调控系统软件调整转速为90 r/min,随着秸秆被逐渐压块成型为颗粒,实现了主轴减负荷试验。
图11 模拟收获试验
Fig.11 Simulated harvest test
增减负荷试验结果及控制器性能对照如图12与表2所示,在调控系统软件发出转速控制指令后,主控制器在GPC-ILC算法下控制液压变速装置调整主轴转速,在3.1～4.5 s主轴转速出现超调现象,超调量为3.32%,主要由转速控制的惯性导致,随后转速进入稳定状态。在铺设秸秆100 m处,单位面积秸秆质量变大,转速略有下降后,进入调整模式,超调量为2.51%,4.78 s内调至目标转速,最大动态偏差为3.21 r/min,与目标值偏差为2.6%,最大余差为1.23 r/min。模拟收获完成时,立即通过软件调整转速为90 r/min,此时成型机料仓内秸秆随着颗粒生产在逐渐减少,模拟减负荷发生在200 s时,秸秆喂入量减小,经过3.52 s调控后转速进入稳定状态,产生2.12%超调量,最大动态偏差为2.23 r/min,与目标值偏差为2.47%,最大余差为0.89 r/min。
表2 控制器性能指标参数
Tab.2 Controller performance indicators parameters
控制算法调节时间/s超调量/%开始增负荷减负荷开始增负荷减负荷GPC-ILC5.324.783.523.322.512.12GPCPID7.6410.526.578.624.534.975.135.502.743.352.242.93
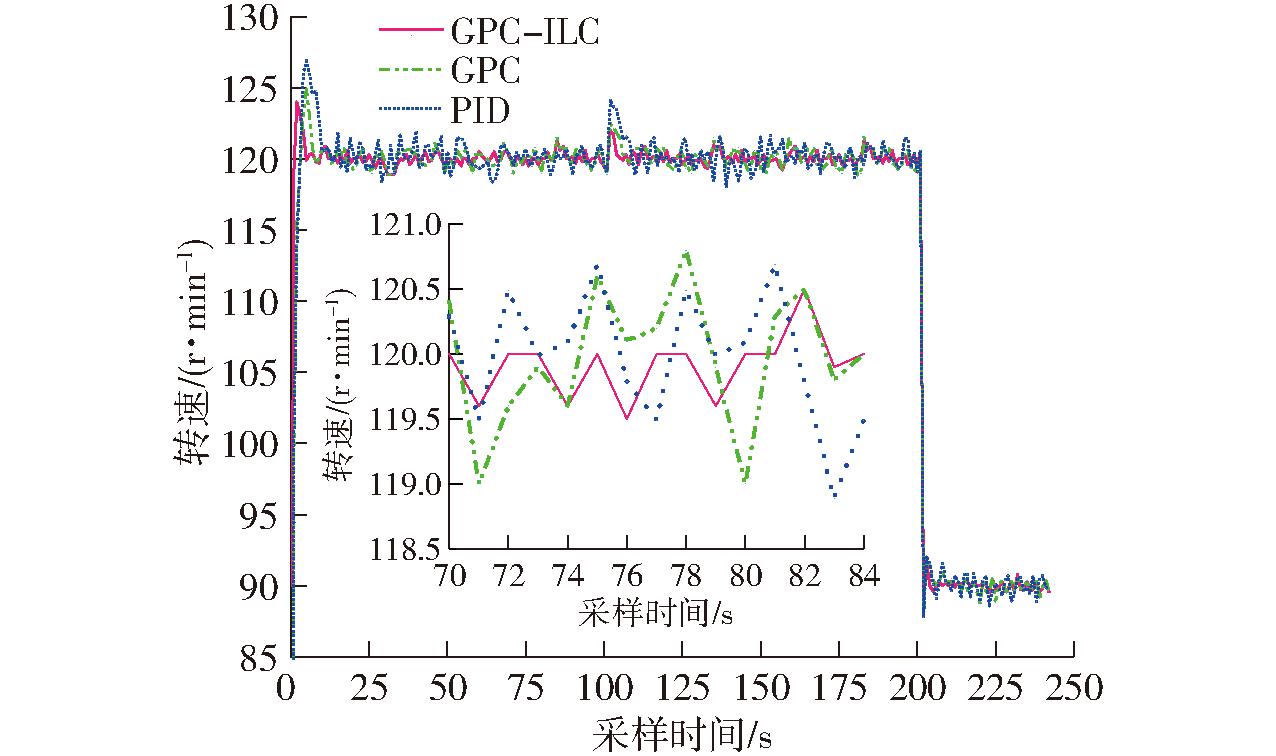
图12 增减负荷试验转速变化曲线
Fig.12 Speed variation curves of increasing or decreasing load test
GPC算法调控时,在开始调速、秸秆增负荷与秸秆减负荷3个过程中调整时间比GPC-ILC算法多2.32、1.79、1.61 s,超调量高1.81、0.23、0.12个百分点。PID算法相对于GPC算法与GPC-ILC算法在开始调速、秸秆增负荷与秸秆减负荷3个过程中调整时间长,超调量较大。3种算法增减负荷的转速误差跟踪曲线如图13所示,可得GPC-ILC算法误差最小,平均误差为0.82 r/min。GPC-ILC算法在增减负荷控制中,具有响应速度快、超调量小和控制精度高的优点,可有效解决秸秆压块成型机转速调控问题,提高秸秆颗粒生产效率与成型率。
图13 增减负荷试验转速误差曲线
Fig.13 Speed error curves of increasing or decreasing load test
田间试验如图14所示,作业前调整车速0.5 m/s,通过工控机调控软件向主控制器写入主轴转速120 r/min,致密成型机收获秸秆并进行田间制粒,在3.1～6.5 s主轴转速出现超调现象,超调量为5.32%,略大于场地试验超调量,随后系统进入稳定调节,在40～50 s内由于田地坑洼不平,转速在117.13～123.75 r/min范围内波动。最大动态偏差为3.75 r/min,与目标值偏差为3.47%,最大余差为1.79 r/min,如图15所示。转速误差变化曲线如图16所示,平均误差为1.52 r/min,大于场地试验平均误差。
图14 田间试验
Fig.14 Field experiment
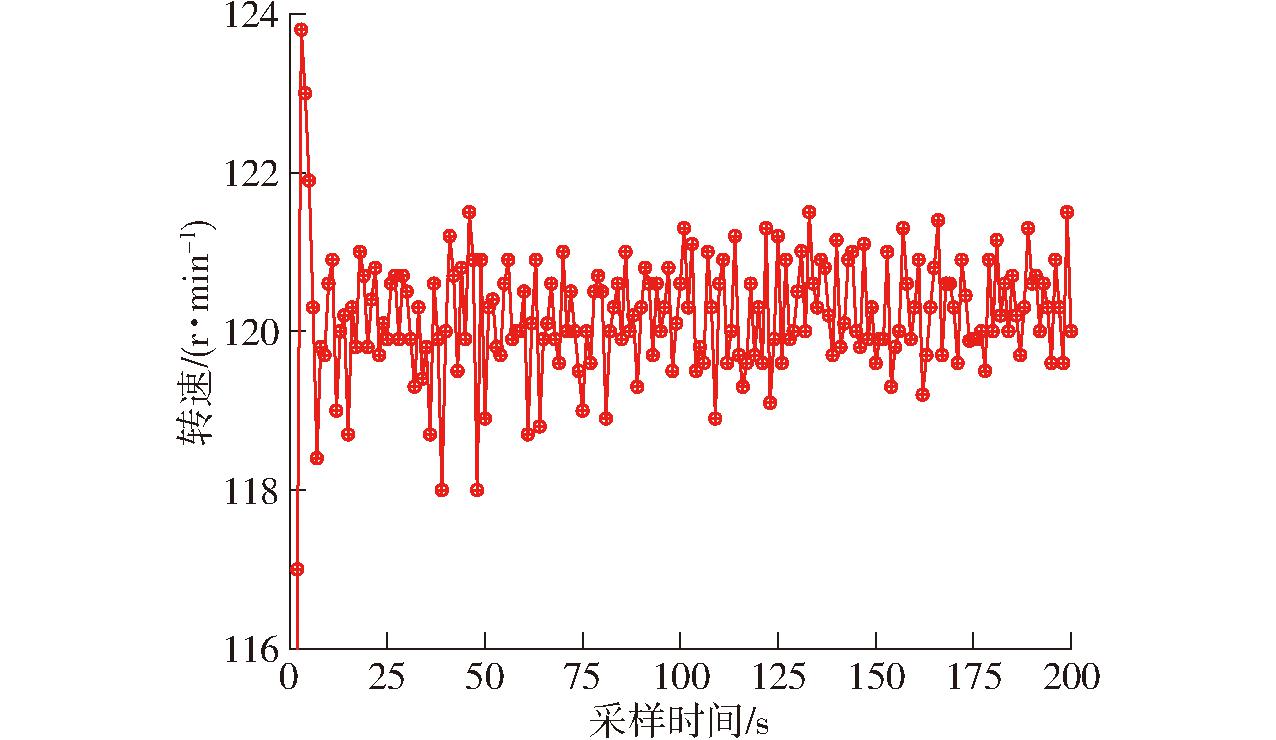
图15 转速变化曲线
Fig.15 Speed variation curve
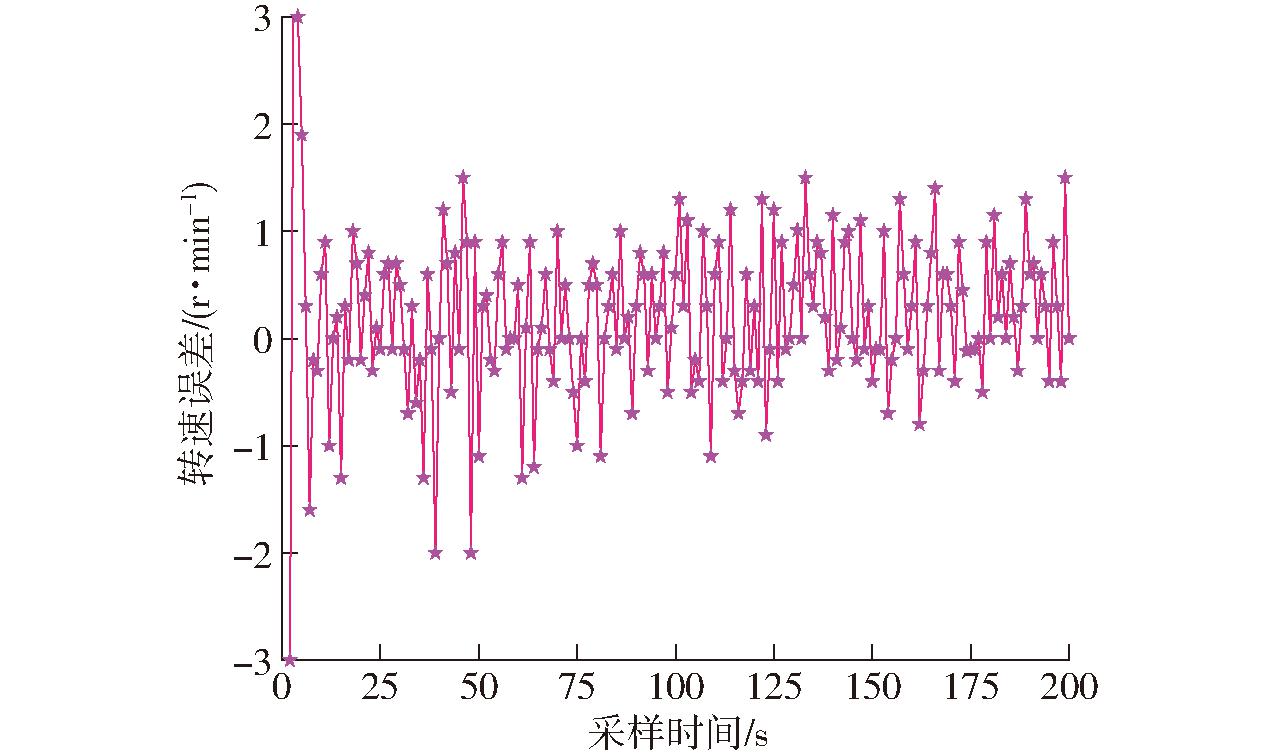
图16 转速误差变化曲线
Fig.16 Speed error variation curve
(1)设计了一种基于GPC-ILC的转速控制系统,建立了预测控制以及液压无级调速系统的数学模型。
(2)在基于GPC-ILC的控制系统中,预测控制运用最小二乘法、滚动优化与反馈校正策略预测输出值,并设计了迭代学习控制,运用累计误差平均的方法优化预测转速输出值。
(3)场地模拟收获试验表明:模拟收获试验增负荷时,转速最大动态偏差为3.21 r/min,与目标值偏差为2.6%,最大余差为1.23 r/min;减负荷时,最大动态偏差为2.23 r/min,与目标值偏差为2.47%,最大余差为0.89 r/min;增减负荷转速达到稳定时间小于5 s,超调量小于3%;田间试验表明:转速最大动态偏差为3.75 r/min,与目标值偏差为3.47%,最大余差为1.79 r/min,平均误差为1.52 r/min,本文设计的控制系统满足移动式作业成型机现场作业的需求。
[1] 霍丽丽,姚宗路,赵立欣,等.秸秆综合利用减排固碳贡献与潜力研究[J].农业机械学报,2022,53(1):349-359.
HUO Lili,YAO Zonglu,ZHAO Lixin,et al.Contribution and potential of comprehensive utilization of straw in GHG emission reduction and carbon sequestration[J].Transactions of the Chinese Society for Agricultural Machinery,2022,53(1):349-359.(in Chinese)
[2] KRZYSIAK Z,ZARAJCZYK J,BARTNIK G,et al.Design of ring granulator for pellet production using CAx techniques[J].Mechanik,2015(2):147-158.
[3] 王咏梅,黄晓鹏,吴劲锋.基于POLYFLOW的环模制粒机流场模拟分析[J].太阳能学报,2017,38(12):3419-3425.
WANG Yongmei,HUANG Xiaopeng,WU Jinfeng.Simulation and analysis of flow field in ring die granulator based on POLYFLOW[J].Acta Energiae Solaris Sinica,2017,38(12):3419-3425.(in Chinese)
[4] 王伟,宫元娟,白雪卫,等.移动式秸秆制粒机作业速度调控系统研究[J].农业机械学报,2021,52(10):186-195.
WANG Wei,GONG Yuanjuan,BAI Xuewei,et al.Investigation on operating speed regulation system of mobile straw granulator[J].Transactions of the Chinese Society for Agricultural Machinery,2021,52(10):186-195.(in Chinese)
[5] 王韦韦,汤君杰,周国安,等.生物质颗粒机组远程监控系统设计与试验[J].农业机械学报,2022,53(12):402-410.
WANG Weiwei,TANG Junjie,ZHOU Guoan,et al.Design and experiment of remote monitoring system for biomass briquetting machine[J].Transactions of the Chinese Society for Agricultural Machinery,2022,53(12):402-410.(in Chinese)
[6] 谭睿.玉米秸秆固化成型试验台设计[D].沈阳:沈阳农业大学,2022.
TAN Rui.Design of corn stalks compact molding test-bed[D].Shenyang:Shenyang Agricultural University,2022.(in Chinese)
[7] 牛峰,高禄辰,胡艳芳,等.基于电机参数失配的模型预测转速控制系统运行稳定性研究[J].电机与控制学报,2023,27(6):55-63.
NIU Feng,GAO Luchen,HU Yanfang,et al.Research on operation stability for model predictive speed control system based on parameter mismatch for motors[J].Electric Machines and Control,2023,27(6):55-63.(in Chinese)
[8] 苗小利,王帅军,郭军.基于模糊WMR-PID算法的无刷直流电机转速调节控制[J].中国工程机械学报,2023,21(1):38-42.
MIAO Xiaoli,WANG Shuaijun,GUO Jun.Speed regulation control of brushless DC motor based on fuzzy WMR-PID algorithm[J].Chinese Journal of Construction Machinery,2023,21(1):38-42.(in Chinese)
[9] CHOI A,AHN H,CHUNG Y,et al.Sliding mode control for sensorless speed tracking of PMSM with whale optimization algorithm and extended Kalman filter[J].Machines,2023,11(1):851-867.
[10] GAO L,CHAI F.Model predictive direct speed control of permanent-magnet synchronous motors with voltage error compensation[J].Energies,2023,16(13):5128-5149.
[11] 张国栋,王红英,卢红平,等.环模特性对饮料颗粒成型率影响探究试验[J].饲料工业,2023,44(7):30-34.
ZHANG Guodong,WANG Hongying,LU Hongping,et al.Study on the influence of ring die on feed particle forming rate[J].Feed Industry,2023,44(7):30-34.(in Chinese)
[12] 孙喜月.玉米秸秆捡拾制粒装置试验研究[D].沈阳:沈阳农业大学,2021.
SUN Xiyue.Experimental study on corn stalk picking and pelleting device[D].Shenyang:Shenyang Agricultural University,2021.(in Chinese)
[13] KHODAVERDIAN M,MALEKZADEH M.Attitude stabilization of spacecraft simulator based on modified constrained feedback linearization model predictive control[J].IET Control Theory and Applications,2023,17(8):953-967.
[14] LIAO H,ZHANG X,MA Z.Robust dichotomy solution-based model predictive control for the grid-connected inverters with disturbance observer[J].CES Transactions on Electrical Machines and Systems,2021,5(2):81-89.
[15] CARLET P G,FAVATO A,BOLOGNANI S,et al.Data-driven continuous-set predictive current control for synchronous motor drives[J].IEEE Transactions on Power Electronics,2022,37(6):6637-6646.
[16] LIU H,YAN S C,SHEN Y,et al.Model predictive control system based on direct yaw moment control for 4WID self-steering agriculture vehicle[J].Int.J.Agric.&Biol.Eng.,2021,14(2):175-181.
[17] LI B,RIAZ S,ZHAO Y.Experimental validation of iterative learning control for DC/DC power converters[J].Energies,2023,16(18):6555-6571.
[18] 肖鹏飞,倪何,金家善.基于MWSA的热力系统单参数时序预测方法[J].上海交通大学学报,2023,57(1):36-44.
XIAO Pengfei,NI He,JIN Jiashan.Sequential prediction method of single parameter for thermal system based on MWSA[J].Journal of Shanghai Jiao Tong University,2023,57(1):36-44.(in Chinese)
[19] 姜兴旺.表示函数与丢番图方程[D].南京:南京师范大学,2021.
JIANG Xingwang.Representation function and diophantine equation[D].Nanjing:Nanjing Normal University,2021.(in Chinese)
[20] YANG W,XU D,JIN L,et al.Robust model predictive control for linear systems via self-triggered pseudo terminal ingredients[J].IEEE Transactions on Circuits and Systems I.Regular Papers,2021,69(3):1312-1322.
[21] ZHANG Z,HE J,ZHENG H,et al.Alternating minimization-based sparse least-squares classifier for accuracy and interpretability improvement of credit risk assessment[J].International Journal of Information Technology &Decision Making,2023,22(1):537-567.
[22] AVERWEG S,SCHWARZ A,SCHWARZ C,et al.3D modeling of generalized newtonian fluid flow with data assimilation using the least-squares finite element method[J].Computer Methods in Applied Mechanics and Engineering,2022,392:114668.
[23] ZHUANG Z,TAO H,CHEN Y,et al.Iterative learning control for repetitive tasks with randomly varying trial lengths using successive projection[J].International Journal of Adaptive Control and Signal Processing,2022,36(5):1196-1215.
[24] SHAHRIARI Z,BERNHARDSSON B,TROENG O.Convergence analysis of iterative learning control using pseudo spectra[J].International Journal of Control,2022,95(1):269-281.
[25] ZHAO X,GENG Y,YUAN C,et al.An unscented Kalman filter-based iterative learning controller for multibody rotating scan optical spacecraft[J].Transactions of the Institute of Measurement and Control,2022,44(12):2418-2433.
[26] 马乐乐.非线性迭代学习模型预测控制研究[D].北京:华北电力大学,2021.
MA Lele.Research on nonlinear iterative learning model predictive control[D].Beijing:North China Electric Power University,2021.(in Chinese)
[27] 王玉刚.非严格重复系统的迭代学习控制方法研究[D].济南:山东大学,2022.
WANG Yugang.Study on iterative learning control methods for non-strictly repetitive systems[D].Ji’nan:Shandong University,2022.(in Chinese)