OSID：
近年来,四旋翼无人机因为具有结构简单、灵活机动和成本低等特点在电力巡检、农业植保和环境检测等领域被广泛使用。然而,四旋翼无人机是一种强耦合、欠驱动的非线性系统,使得四旋翼无人机轨迹跟踪问题面对诸多难题,因此,如何实现具有强鲁棒性并且稳定跟踪期望轨迹,是四旋翼无人机飞行控制系统设计面临的重要挑战[1-3]。
国内外研究人员提出了一系列控制策略以提高四旋翼无人机飞行控制系统的鲁棒性。比如比例-积分-微分(PID)控制[4-6]、滑膜控制[7-8]、自抗扰控制[9]、反步控制[10-11]、神经网络控制[12]等。BECHLIOULIS等[13]提出了预设性能约束控制(Prescribed performance control,PPC)方法,使用一种指数衰减型性能函数,通过误差转换方程将实际的跟踪误差与性能函数相关联,并且保证跟踪误差可以保持在预设的范围内,因此具有良好的稳态和瞬态性能。基于PPC方法,CUI等[14]通过固定时间指令滤波器,消除了传统反步法中存在的“微分爆炸”现象,同时通过一种新的分数阶功率误差补偿机制消除了滤波误差的影响,将预设性能控制和反步设计方法与指令滤波技术相结合,建立了固定时间自适应控制策略。WU等[15]提出了一种新的有限时间控制策略,实现了对期望姿态的有限时间跟踪,并且不需要系统参数已知的一些假设。ZHANG等[16]针对四旋翼飞行器提出了一种基于未知输入观测器的指定时间漏斗控制,提出了一个由连续分段函数组成的指定时间漏斗界来保证跟踪误差收敛到包络,并提出了一个修正的漏斗变量来克服奇异性问题。SHEN等[17]针对具有输入约束、模型不确定性和未知干扰的四旋翼无人机轨迹跟踪问题对预设性能控制展开研究。为了减小饱和效应,使四旋翼无人机的状态满足预设性能,引入辅助方程,同时通过新颖的误差变换将原约束系统转化为等价的无约束系统。SHAO等[18]针对四旋翼飞行器轨迹跟踪问题,提出了一种具有预设性能的事件触发抗干扰控制。通过所提出的改进的预设性能控制(Modified prescribed performance control,MPPC),可以在不牺牲收敛速度的情况下实现改进的预定瞬态性能,即更小的超调量。综上所述,由于四旋翼无人机是一个强耦合、欠驱动的6自由度的非线性系统,很容易受到内部和外部干扰从而导致飞行状态失稳,因此预设性能控制方法由于其优良的瞬态和暂态性能,在无人机控制领域得到了广泛研究。
由于神经网络具有很强的自学习能力、非线性映射能力,可以逼近任意非线性函数,被广泛应用于复杂系统的控制中。径向基神经网络(Radial basis function neural network,RBFNN)是一类特殊的神经网络结构,在应用于系统控制时,可基于 Lyapunov 稳定性定理设计自适应率,用以迭代更新 RBF 神经网络的链接权重。RAZMI等[19]将神经网络自适应方案与滑模控制相结合,为每个子系统设计相应的滑模控制器,并通过神经网络方法自适应地调整滑模控制器在滑动流形上的系数。ZHANG等[20]考虑到RBF神经网络的强逼近性,提出了基于指定时间神经网络的控制方案来补偿外部扰动和参数不确定性。SHI等[21]和LIU等[22]考虑了针对一类存在外部扰动的非线性系统,提出了一种基于RBF神经网络的自适应反步动态面控制方法,基于自适应控制的RBF神经网络被用来任意逼近未知的光滑函数。
为了解决四旋翼无人机的不确定数学模型难以精确建立,并且在执行任务过程中存在外部未知扰动的问题,本文提出一种基于指定时间预设性能约束控制方法,并且利用RBF神经网络逼近补偿外部未知扰动,将预测结果补偿给控制器以提高鲁棒性。通过Matlab/Simulink 仿真验证所提出的方法应用于无人机控制系统的稳定性和性能优势。
四旋翼无人机是一种欠驱动的6自由度四旋翼无人机。以十字形四旋翼无人机为研究对象,将四旋翼无人机模型简化为如图1所示的结构。在飞行过程中,通过调节四旋翼无人机的4个电机转速产生力矩,从而实现无人机位置姿态的改变。
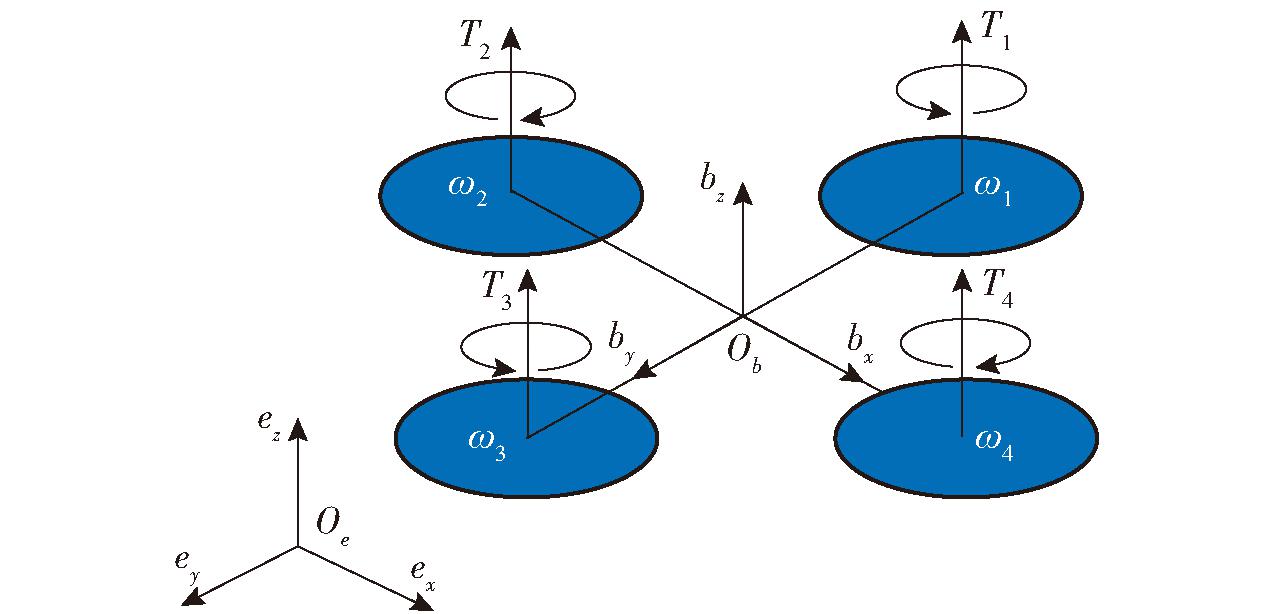
图1 四旋翼无人机结构示意图
Fig.1 Schematic of quadrotor UAV structure
四旋翼无人机姿态系统模型满足如下假设:①四旋翼无人机为刚性结构且结构对称,其质心与机体坐标系重合。②每个旋翼产生的升力和受到的反扭矩都与旋翼的转速平方成正比。③四旋翼无人机角速度为姿态角的导数。
如图1所示,建立惯性坐标系E={ex,ey,ez}与无人机机体坐标系B={bx,by,bz},用以描述无人机在空间中的位姿。φ、θ、ψ分别表示无人机的俯仰角、横滚角、偏航角,ω1、ω2、ω3、ω4为电机1、2、3、4的角速度。根据牛顿-欧拉方程建立具有外部扰动和模型不确定性的四旋翼无人机系统数学模型[23-24]
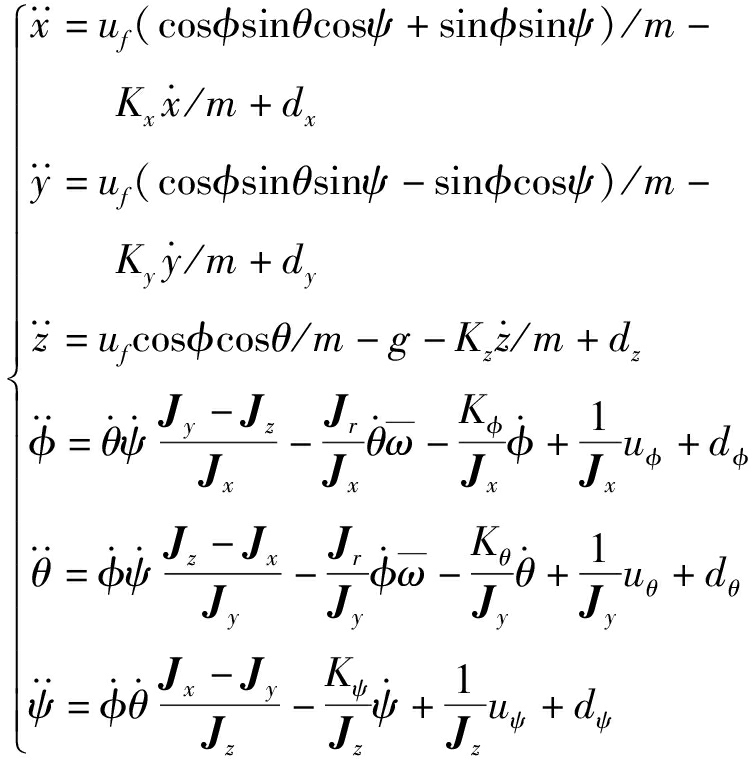
(1)
式中 m——四旋翼无人机质量
g——重力加速度
Kx——x方向的位置阻力系数
Ky——y方向的位置阻力系数
Kz——z方向的位置阻力系数
Kφ——俯仰角姿态阻力系数
Kθ——横滚角姿态阻力系数
Kψ——偏航角姿态阻力系数
Jx、Jy、Jz——x、y、z轴上的惯性矩阵
uf——系统x、y、z轴总体的控制输入量
uφ——系统俯仰角控制输入
uθ——系统横滚角控制输入
uψ——系统偏航角控制输入
dx——无人机x轴扰动量
dy——无人机y轴扰动量
dz——无人机z轴扰动量
dφ——无人机俯仰角扰动量
dθ——无人机横滚角扰动量
dψ——无人机偏航角扰动量
整体残余转子角度
方向速度
方向速度
方向速度
俯仰角速度
横滚角速度
偏航角速度
方向加速度
方向加速度
方向加速度
俯仰角加速度
横滚角加速度
偏航角加速度
径向基函数神经网络(RBFNN)以其优秀的逼近性能在各个领域获得了广泛关注。针对四旋翼无人机的参数不确定性、未知信息以及集总扰动等因素,使其难以得到良好的轨迹跟踪控制性能,因此考虑到RBFNN具有足够精度的逼近性能,用于逼近的无人机受到的外部扰动和参数不确定性RBFNN逼近函数f(x)定义为
f(x)=W*Th(x)+μ(x) (∀x∈R)
(2)
其中
(3)
式中 h(x)——逼近误差
μ(x)——神经网络逼近误差
W*——理想权重
(4)
式中 cj、bj——高斯函数的中心值和宽度
考虑到四旋翼无人机是欠驱动系统,本文采用双层控制结构设计轨迹跟踪控制器:外层根据位置参考信号Pr(xr,yr,zr)计算平移运动所需的俯仰角θr、横滚角φr以及总升力F,内环姿态控制器跟踪外环提供的参考姿态角计算旋转力矩Γ。
本文所使用的性能约束控制方法是通过一个指数衰减型性能函数约束跟踪误差,保证跟踪误差被限制在预设范围内。然而传统的指数衰减型性能函数只能确保被约束的函数在无限的时间内收敛到预设的范围内,并不能在指定的时间内收敛。因此,为了在指定时间内获得更好的跟踪性能,引入指定时间预设性能函数,指定时间预设性能函数定义为
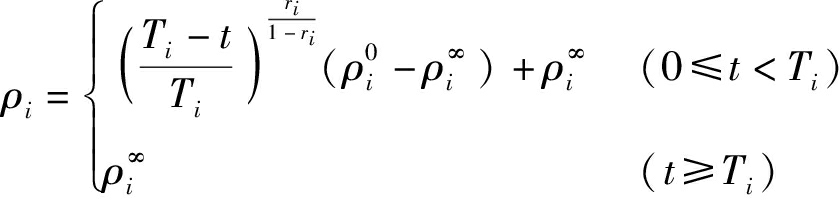
(5)
其中
ri=l1-l2cos(πt/Ti)
ρi对时间的导数为
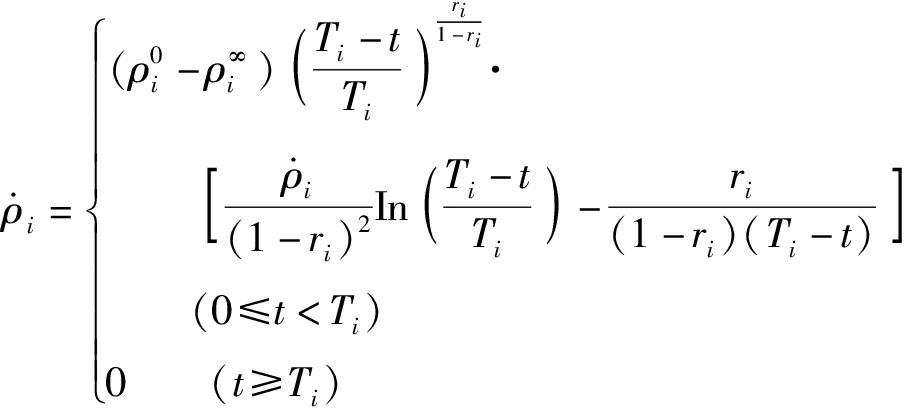
(6)
式中 
性能函数导数
性能函数常量
性能函数常量值域
Ti——自由设置的时间参数
t——时间
l1、l2——预设性能常数
基于提出的性能函数,位置跟踪误差变量ei的边界约束为
(7)
式中
常数
式(7)的初始值为
(8)
由于预设性能函数(6)不能直接用于设计控制器,因此需要用一个误差转换函数来将跟踪误差和指定时间性能函数联系起来,考虑误差转换函数γ(x)满足以下转换函数条件:单调递增函数;
其中
(9)
式中 ει——转换后的误差
ι取p、a,分别表示对应的姿态和位置。
由图2可知,由于式(9)满足条件,它可以作为一个变换函数,并且当εi趋于0时,γi(εi)收敛于0。此外,与文献[5]中的误差转换函数γi(εi)=
其中κi为常数)相比,当εi从无穷大趋近于0时,误差转换函数(9)具有更快的收敛速度。
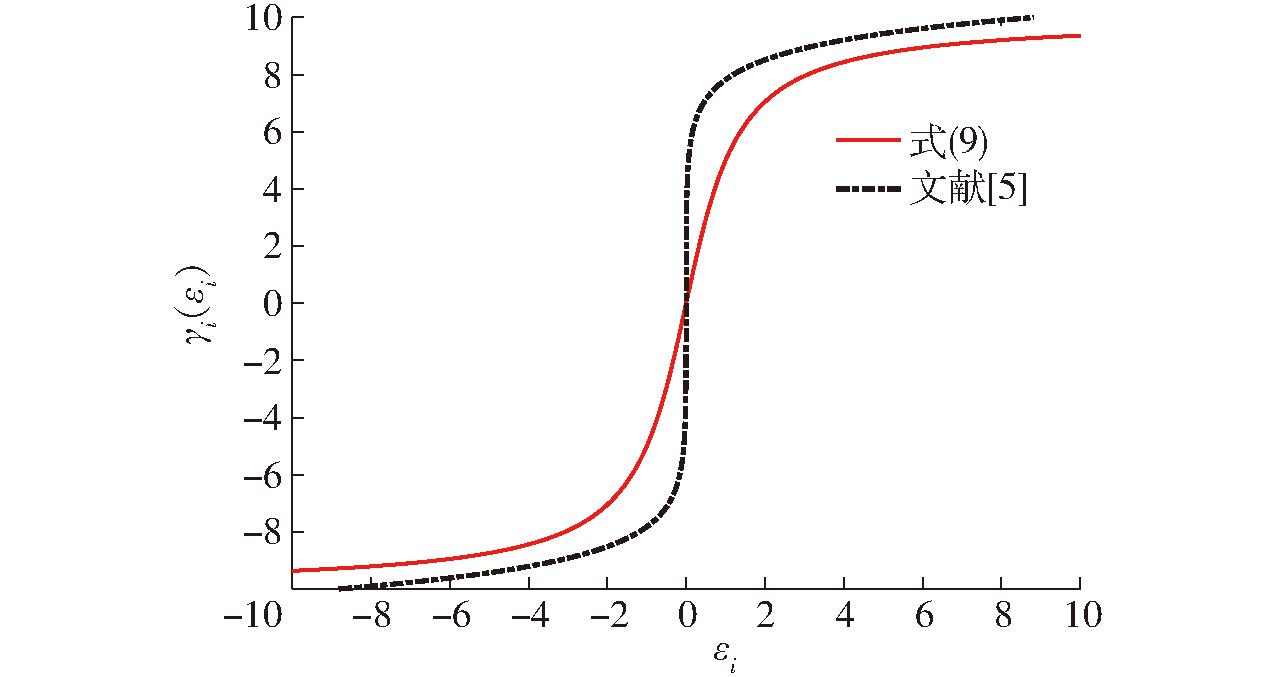
图2 两种误差转换函数收敛速度比较
Fig.2 Comparison of convergence speed of two error transformation functions
在不违反性能函数约束要求的情况下,提出一种新型的滤波误差补偿系统
(10)
(11)
设计的虚拟控制率为
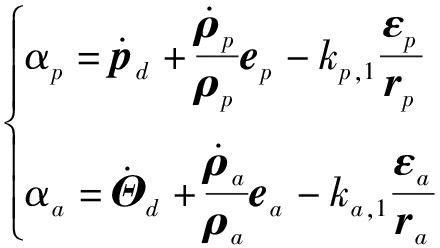
(12)
式中 αp——位置系统虚拟控制律
αa——姿态系统虚拟控制律
kp,1——位置系统虚拟控制律设计参数
ka,1——姿态系统虚拟控制律设计参数
下标p表示x、y、z,a表示φ、θ、ψ。
为避免对虚拟控制信号求导时发生“参数爆炸问题”,采用一阶滤波器
(13)
其中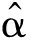
ι为αι的估计值。
结合式(10)～(13),设计含有新型滤波误差补偿系统的控制器
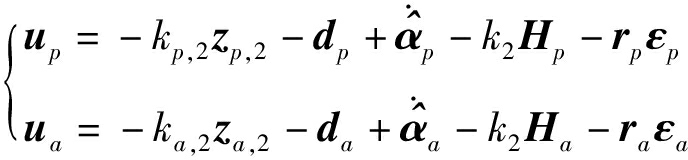
(14)
式中 kp,2、ka,2——设计参数
虚拟控制律估计值的导数
所设计的控制策略原理如图3所示。
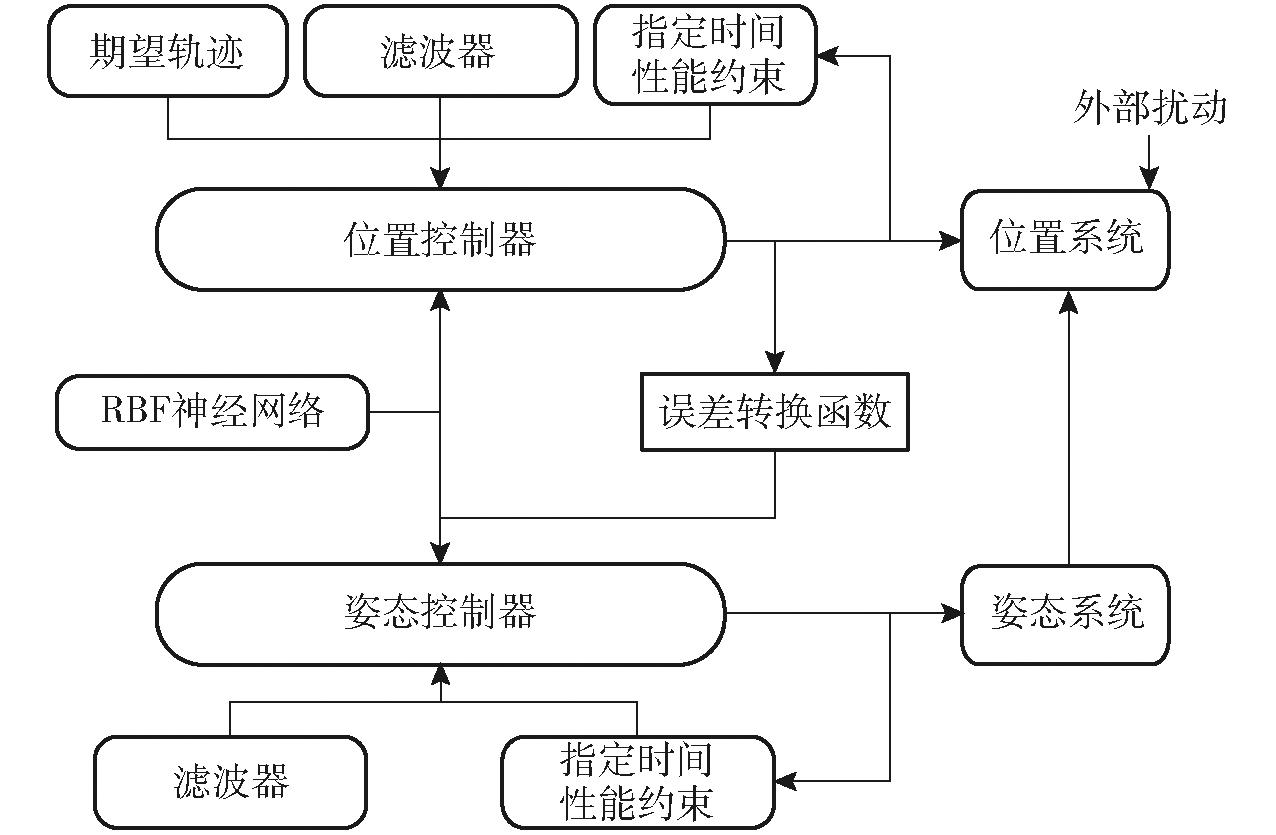
图3 控制策略原理图
Fig.3 Schematic of control strategy
为了简化后续证明,无人机模型可简化为
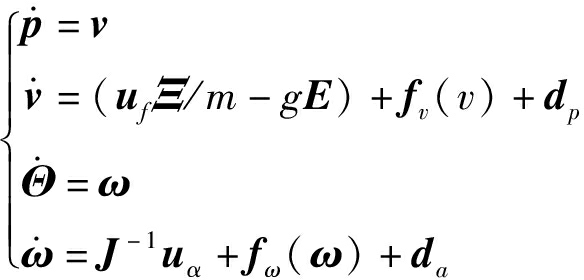
(15)
式中
p={x,y,z} Θ={φ,θ,ψ}
Ξ=[(cosφsinθcosψ+sinφsinψ)/m,
(cosφsinθsinψ-sinφcosψ)/m,cosφcosθ/m]T
da={dφ,dθ,dψ} dp={dx,dy,dz}
为补偿无人机未知连续的非线性部分和外部环境干扰对控制器性能的影响,引入RBFNN逼近策略
(16)
式中:xp={p,v,ep,ev},xa={Θ,ω,eΘ,eω};hι(xι)为神经网络自适应率的中心函数;μι为逼近误差。
设计逼近函数为
(17)
权重的误差矩阵为
(18)
式中
权重估计值
对未知动态函数dp={dx,dy,dz},da={dφ,dθ,dψ},其中包括未知连续性的非线性部分以及外部扰动,利用RBFNN逼近该非线性动态函数。
实际的控制器设计为
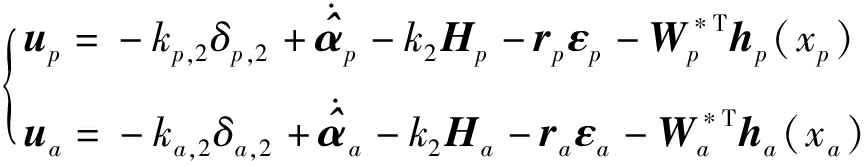
(19)
神经网络自适应率设计为
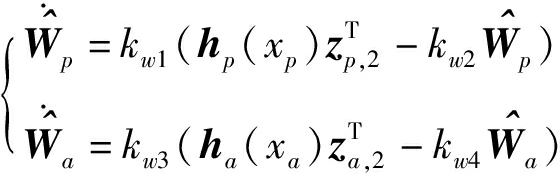
(20)
式中 kw1、kw2、kw3、kw4——自适应率增益
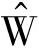p——位置系统神经网络自适应律
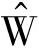a——姿态系统神经网络自适应律
定义补偿后的误差信号δ1=ε-χ1,构造Lyapunov函数以证明位置误差跟踪系统的稳定性,即
(21)
对V1求导可得
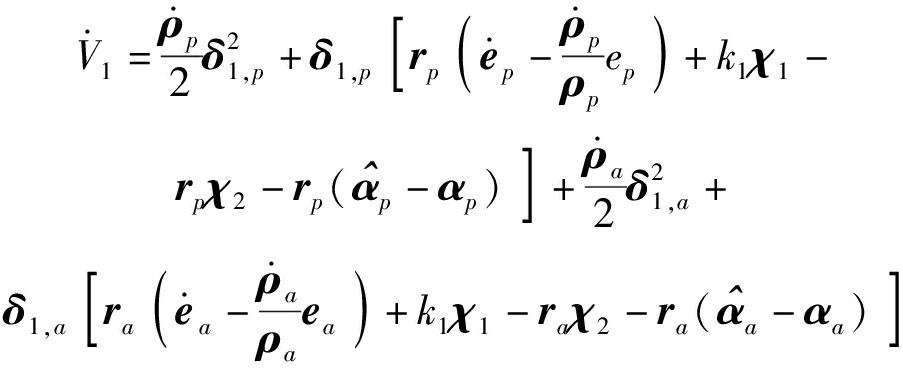
(22)
定义虚拟误差
H=ev-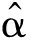
(23)
将式(10)、(12)和虚拟误差H代入到式(22),定义δ2=H-χ2,V1的导数可表示为
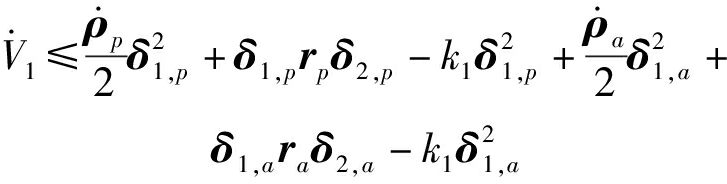
(24)
为证明速度跟踪误差的稳定性,构造Lyapunov方程
(25)
对式(25)进行求导得
(26)
将式(11)、(15)、(23)代入式(26)可得
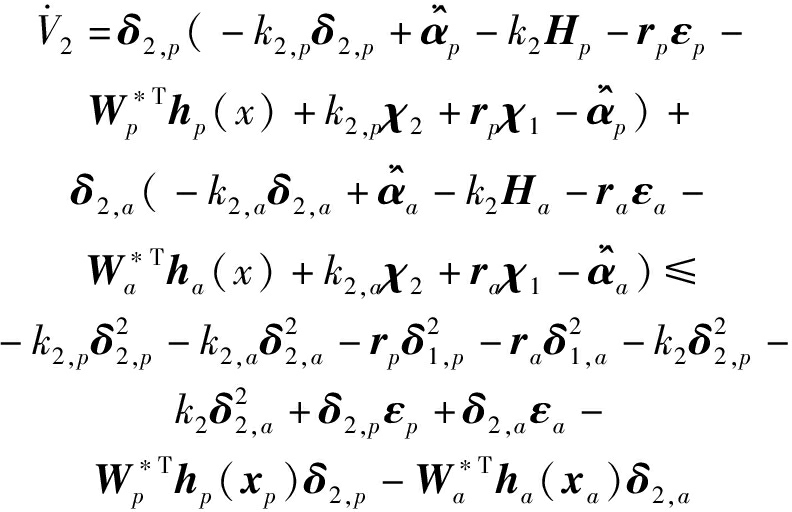
(27)
基于式(20),为证明整个无人机动态系统的稳定性,建立Lyapunov方程
(28)
对式(28)求导可得
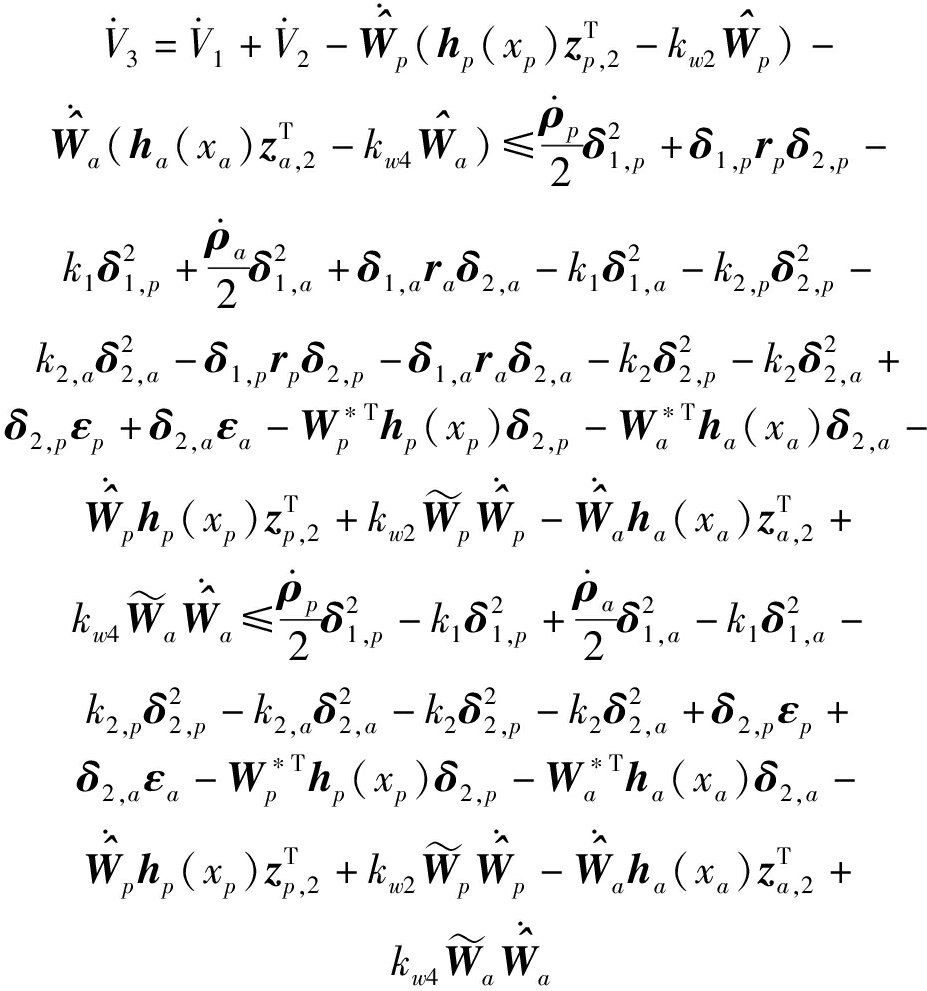
(29)
根据杨氏不等式可得
(30)
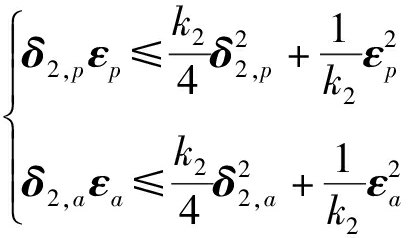
(31)
式(29)转化为
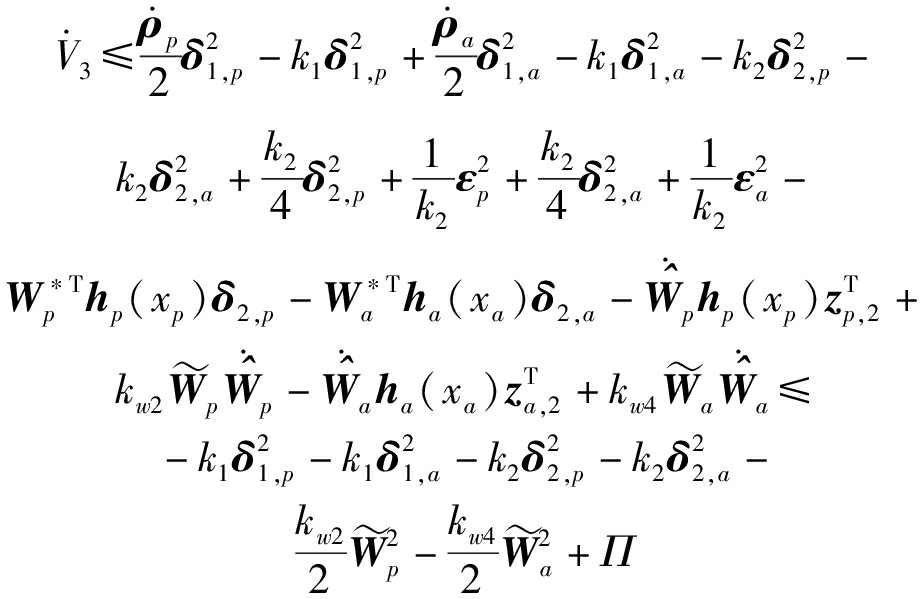
(32)
其中
式(32)可以进一步简化为
(33)
其中
从式(33)的稳定性分析可知,
都是有界的并且指定时间稳定的。本文所涉及到的自定义最佳参数均由Matlab/Simulink仿真中使用试凑法得出。
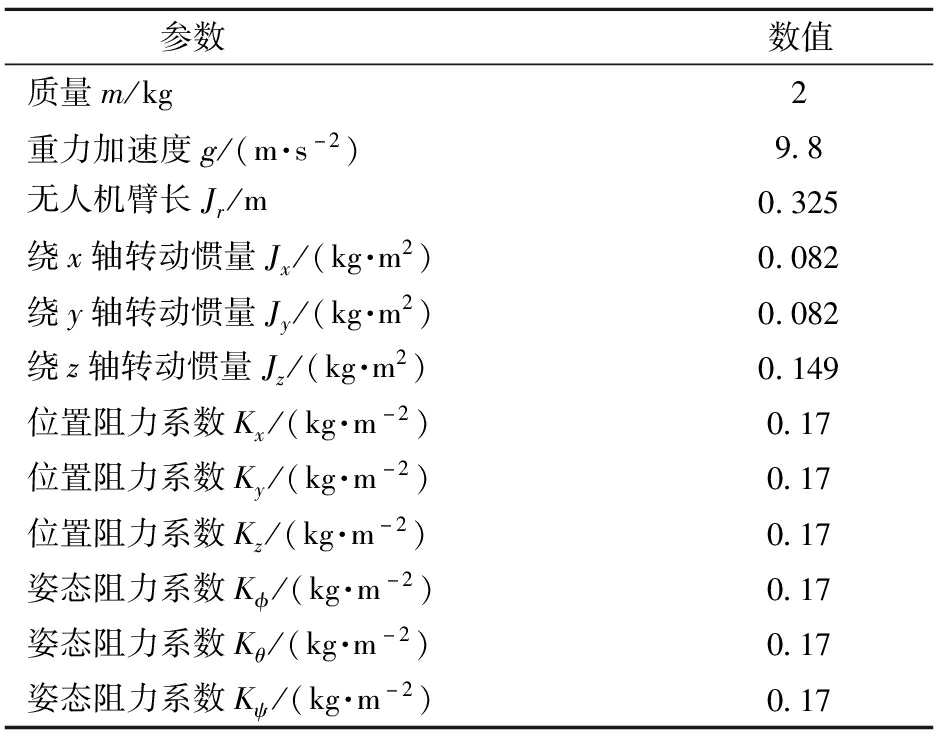
为了验证上述控制算法的有效性,在Matlab/Simulink环境中,搭建四旋翼无人机系统模型,并进行仿真试验。本试验的四旋翼无人机动力学参数和性能约束控制器参数如表1和表2所示。
表1 四旋翼无人机动力学参数
Tab.1 Dynamic model parameters of UAV
参数数值质量m/kg2重力加速度g/(m·s-2)9.8无人机臂长Jr/m0.325绕x轴转动惯量Jx/(kg·m2)0.082绕y轴转动惯量Jy/(kg·m2)0.082绕z轴转动惯量Jz/(kg·m2)0.149位置阻力系数Kx/(kg·m-2)0.17位置阻力系数Ky/(kg·m-2)0.17位置阻力系数Kz/(kg·m-2)0.17姿态阻力系数Kϕ/(kg·m-2)0.17姿态阻力系数Kθ/(kg·m-2)0.17姿态阻力系数Kψ/(kg·m-2)0.17
表2 控制参数
Tab.2 Control parameters
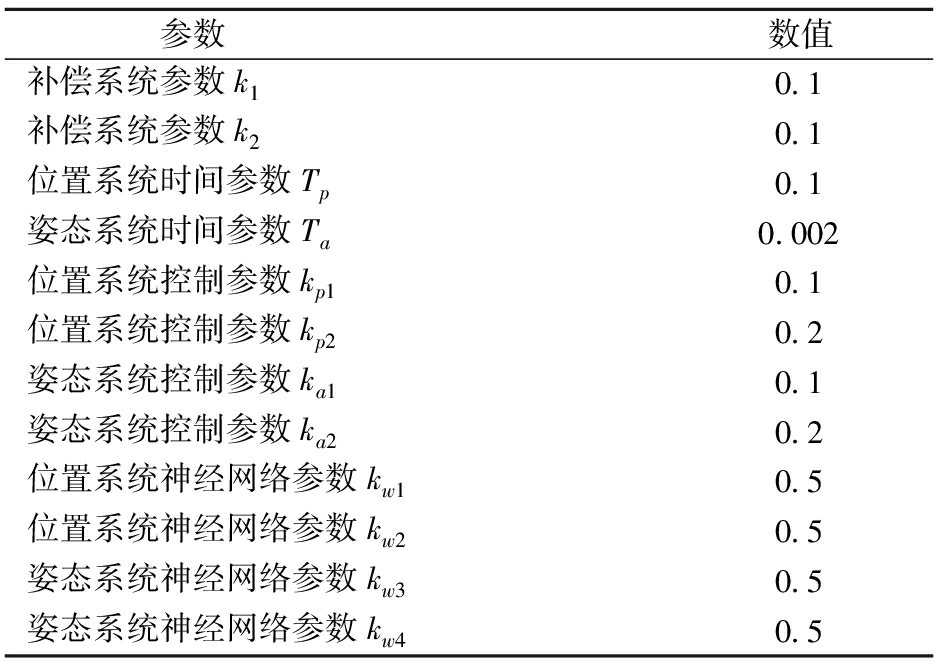
参数数值补偿系统参数k10.1补偿系统参数k20.1位置系统时间参数Tp0.1姿态系统时间参数Ta0.002位置系统控制参数kp10.1位置系统控制参数kp20.2姿态系统控制参数ka10.1姿态系统控制参数ka20.2位置系统神经网络参数kw10.5位置系统神经网络参数kw20.5姿态系统神经网络参数kw30.5姿态系统神经网络参数kw40.5
圆形期望轨迹为
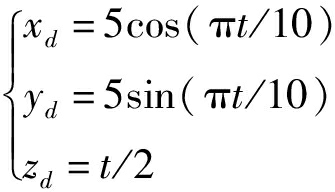
(34)
设置外部环境时变干扰为
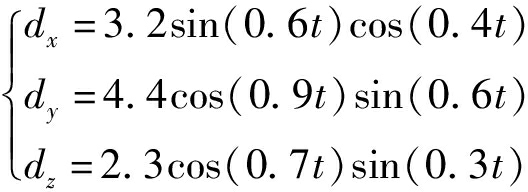
(35)
(36)
设置性能函数参数:
初始位置设置为(4,0,1),初始姿态设置为
根据仿真结果,UAV在初始位置的轨迹跟踪效果如图4所示。图5、6分别为位置和姿态系统跟踪误差,图7为位置系统轨迹跟踪曲线。图4～7的结果表明,所设计的控制器具有指定时间收敛能力,且位置和姿态误差可以在指定时间(t=5 s)内收敛到原点附近小邻域,保证了系统瞬态和稳态跟踪性能,图8显示,本文所提出的补偿系统可以较好地避免系统产生滤波误差。
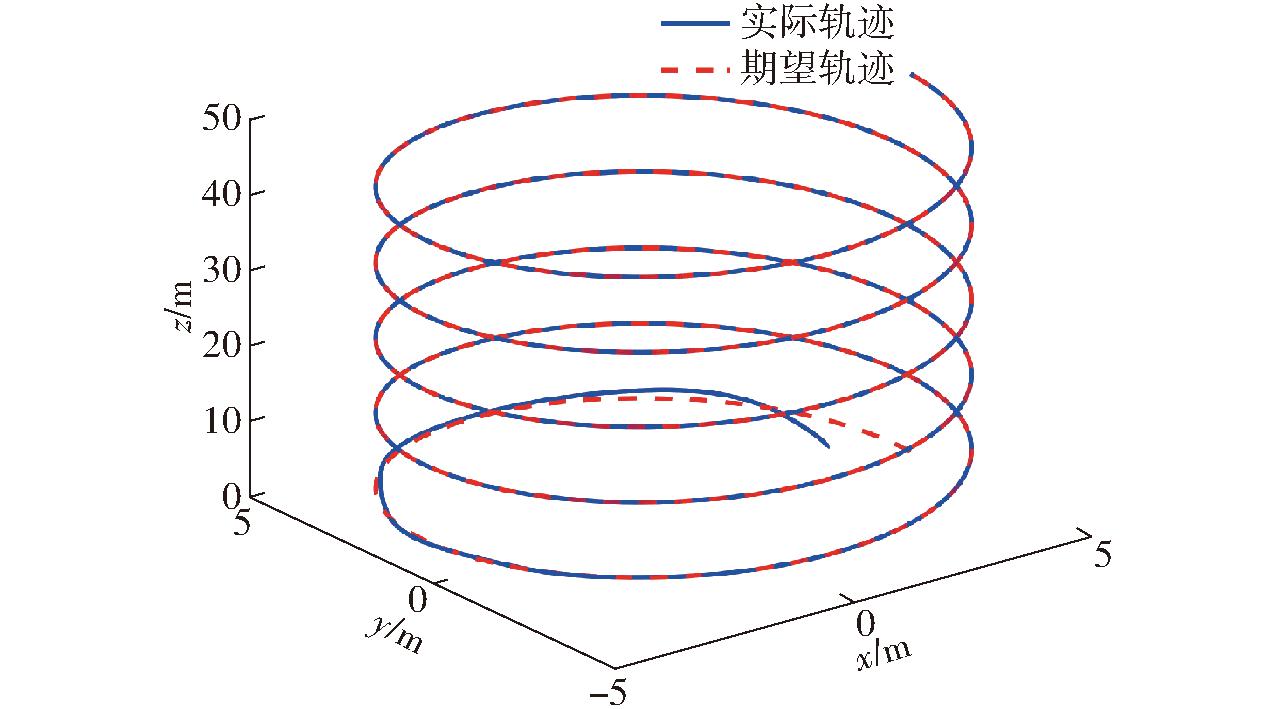
图4 三维轨迹图
Fig.4 3D trajectory diagram
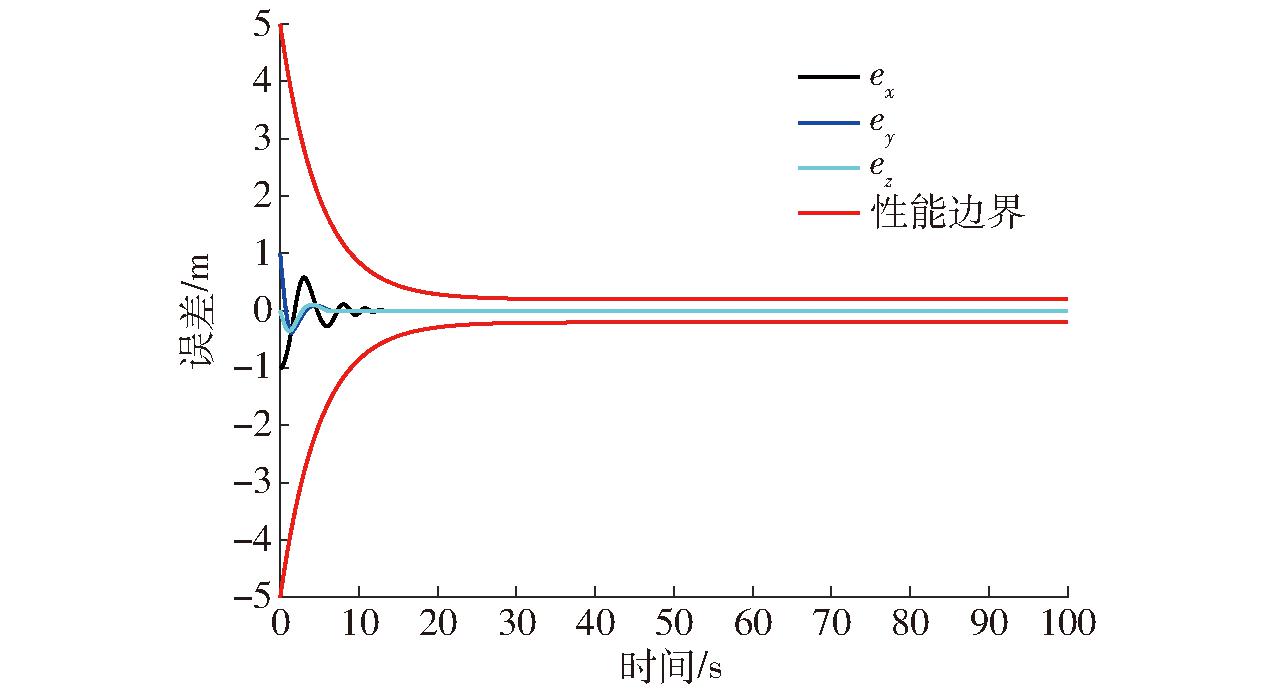
图5 位置系统跟踪误差曲线
Fig.5 Positioning system tracking error
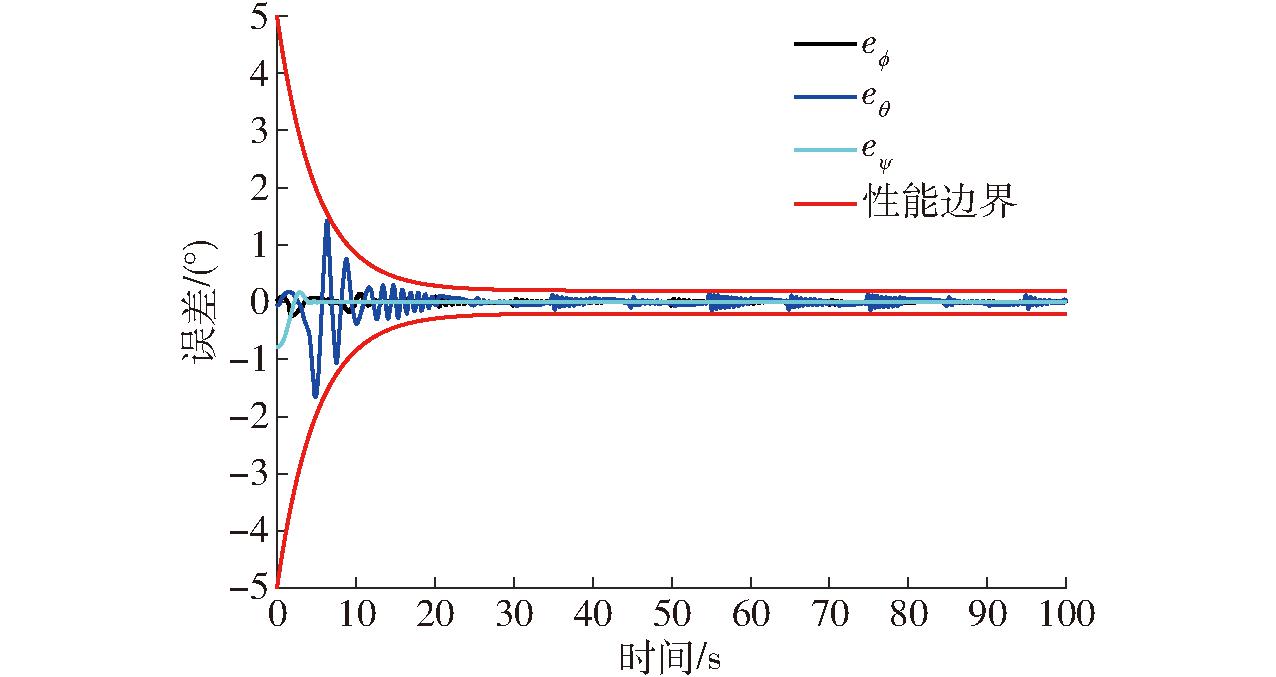
图6 姿态系统跟踪误差曲线
Fig.6 Attitude system tracking error
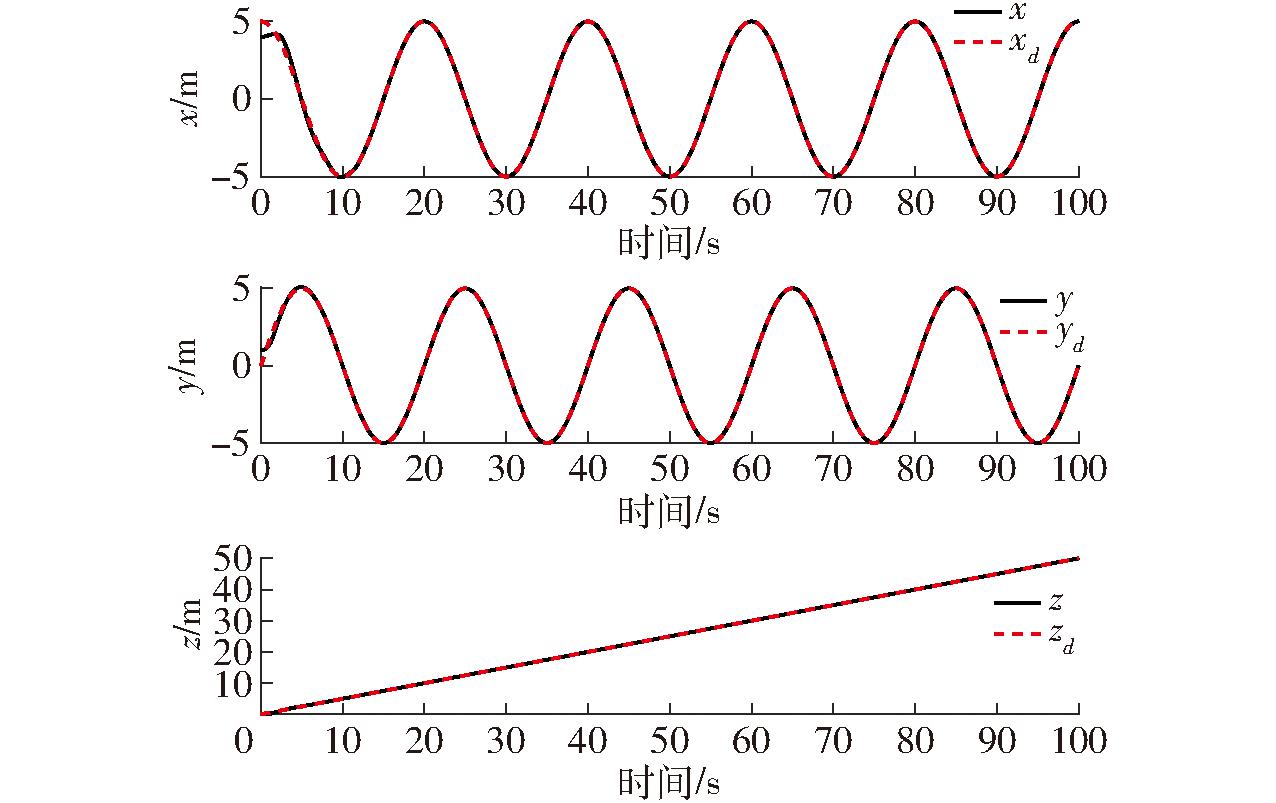
图7 位置系统轨迹跟踪曲线
Fig.7 Position system trajectory tracking curves
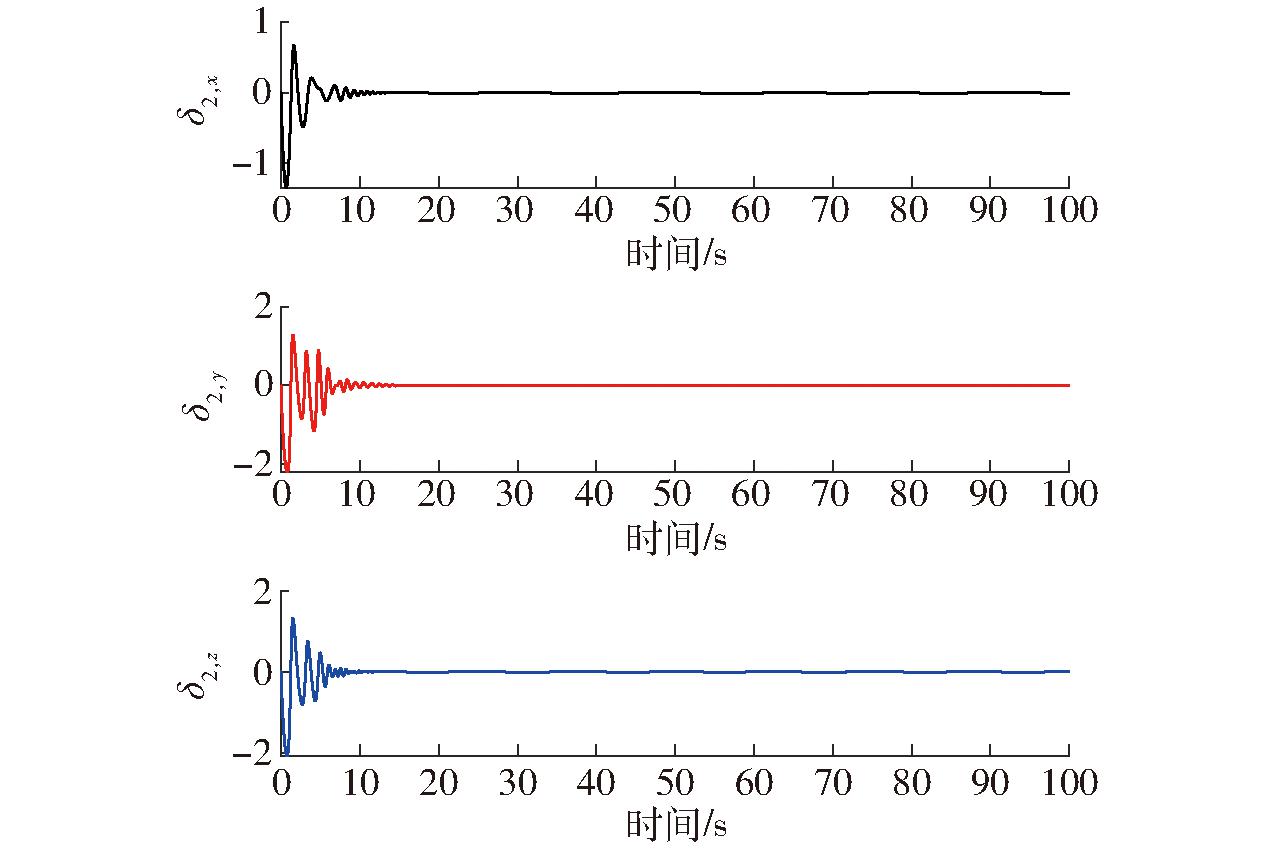
图8 补偿系统误差变化曲线
Fig.8 Compensation system error curves
当存在外部突变误差时,为了进一步验证本文所提出的控制策略鲁棒性,在第20 s时设置较大的突变扰动,其中突变扰动设置为
(37)
第20 s后的扰动为
(38)
图9、10为在突变扰动下无人机位置系统跟踪误差,表明本文所提出的控制器即使在设置突变扰动后仍可以保持良好的跟踪性能。图11为无人机输入力矩变化曲线,在第20 s时出现较大的突变扰动,控制器可以及时反映并调整反馈到无人机系统中。本文所设计的补偿系统,在设置新的突变扰动后,即使在第20 s时出现了较大的突变扰动也能及时补偿突变的扰动误差,保证了无人机系统的稳定性(图12)。
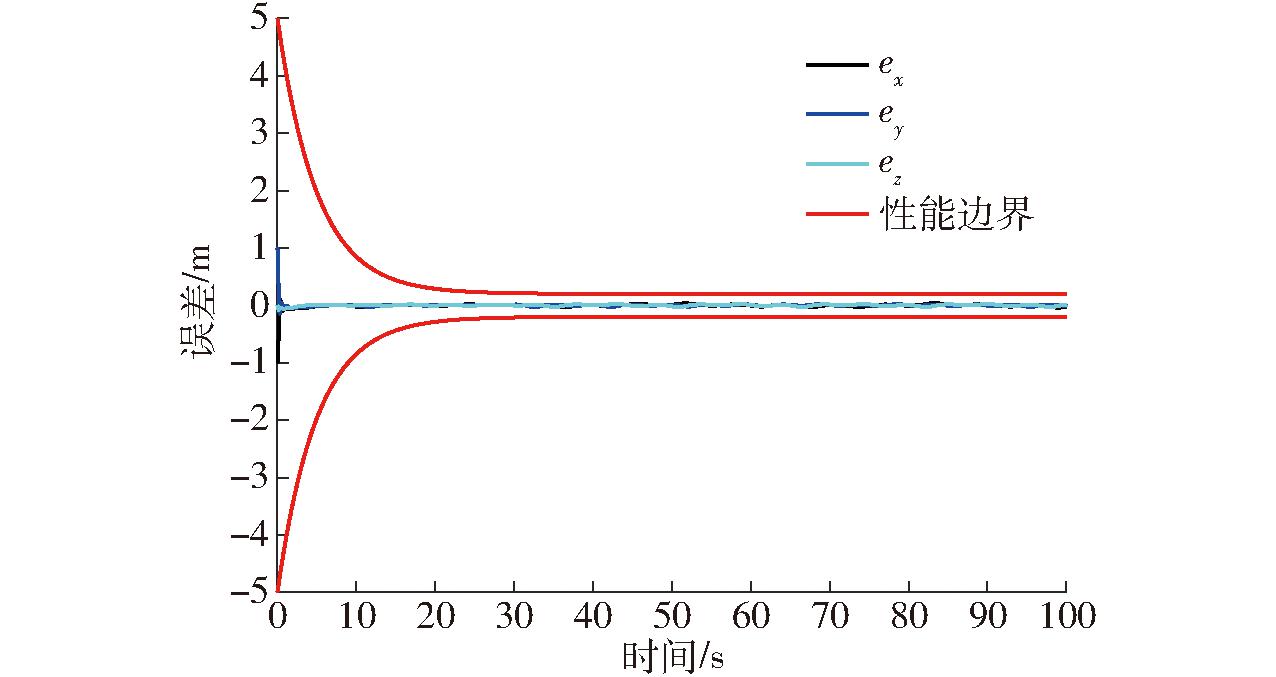
图9 突变扰动下位置系统跟踪误差曲线
Fig.9 Positioning system tracking error curves
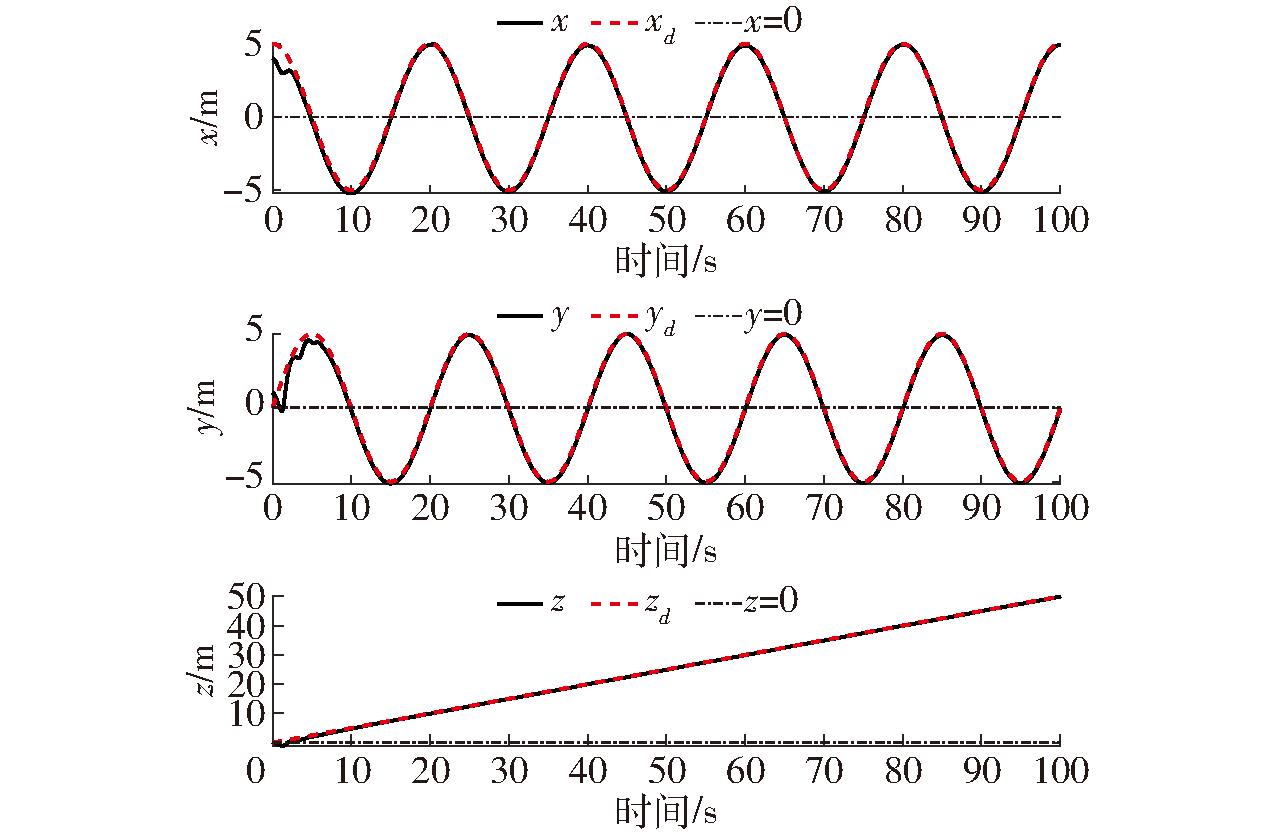
图10 突变扰动下位置系统轨迹跟踪曲线
Fig.10 Position system trajectory tracking curves
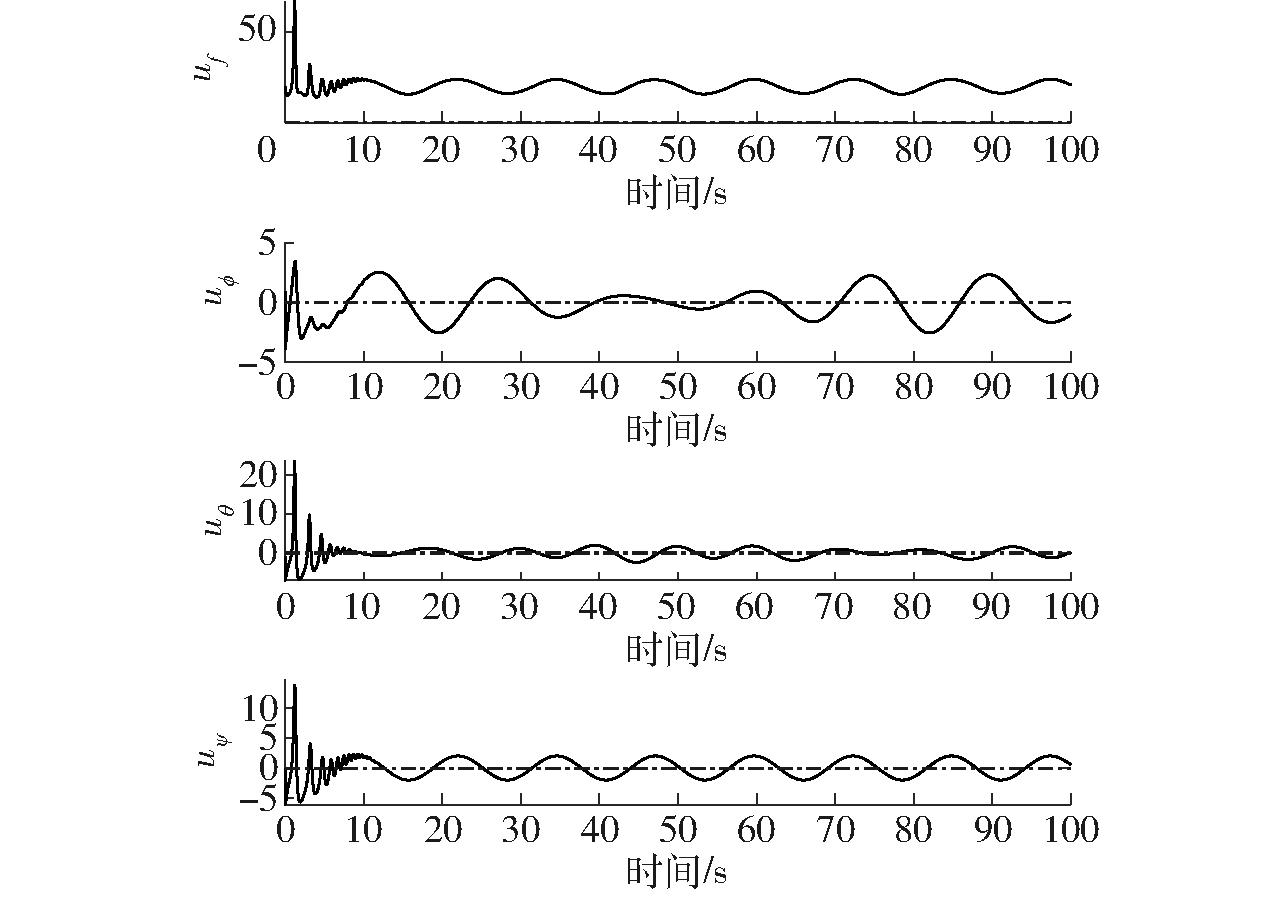
图11 控制输入力矩变化曲线
Fig.11 Control force input curves
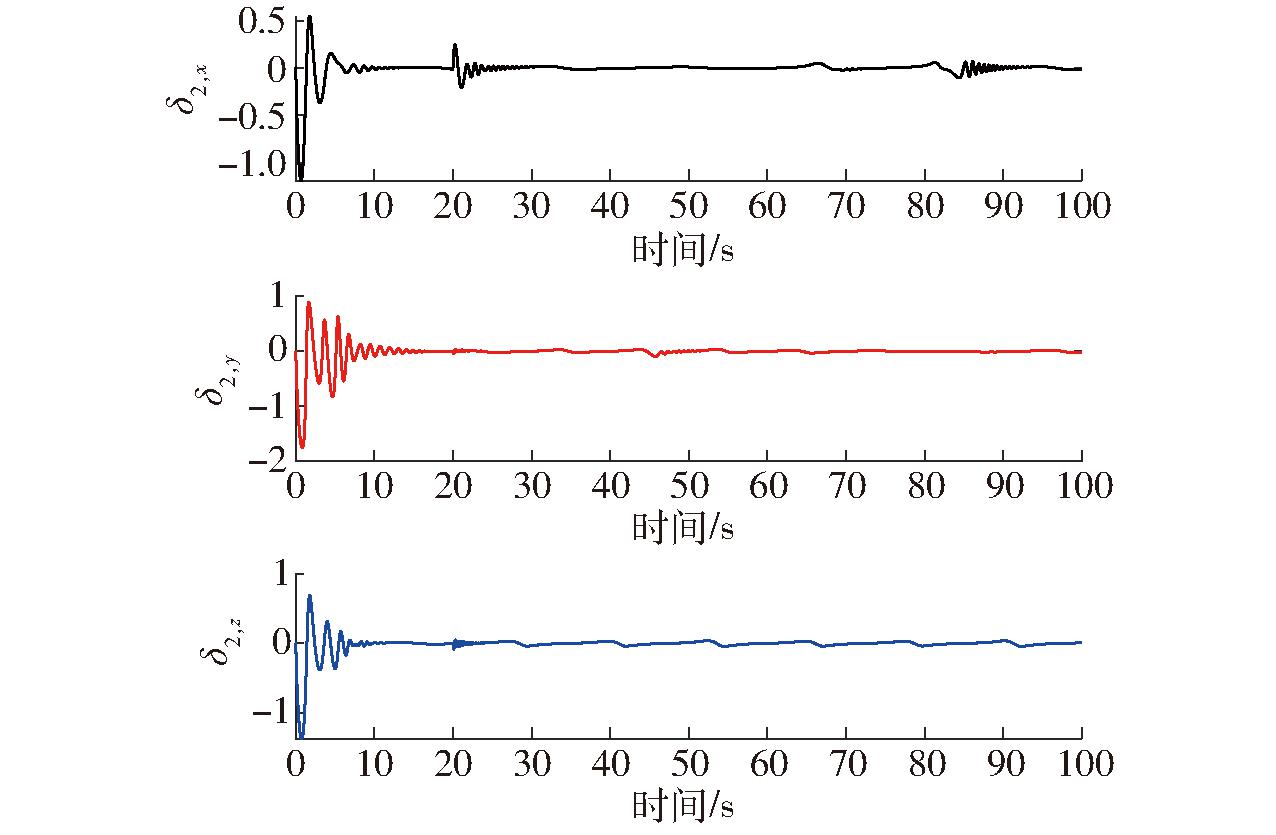
图12 突变扰动下补偿系统误差变化曲线
Fig.12 Compensation system error curves
为进一步验证所设计的控制算法在实际无人机中的有效性,选择干扰较强的自主轨迹跟踪动作进行实际飞行验证,自主轨迹跟踪动作试验如图13所示。设计的控制算法采用C++语言进行编写,在eclipse中编码编译,最后将代码载入到Pixhawk。在本次的实机验证中,所提出的指定时间性能控制算法在飞行试验中的参数与前面章节的仿真模拟参数一致。
图13 悬停和自主轨迹跟踪试验
Fig.13 Hover and autonomous landing experiments
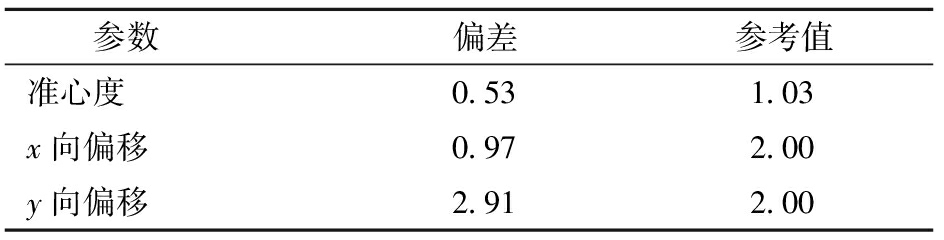
本次试验以陈氏航空120型开源四旋翼无人机为试验机型,飞行试验场地选择在微风聚集扰动环境下的试验基地,限定飞行高度为50 m,分别以无人机起飞位置为起始点,降落位置为终止点,基于Minimum Snap生成了自主跟踪轨迹。将规划好的轨迹按照空间层级定点进行实际的飞行跟踪试验和测试,利用平面误差测量、相对位姿比较和时间同步法分别测试无人机起降位置偏差和实时响应偏差见表3、4。通过与原型机的测试参数比对,飞行过程中,在限定区域内随着无人机飞行高度的不断上升,无人机受到地面电磁挠动的影响会逐渐减小,无人机盘旋上升时风力的变化对无人机的稳定性会有明显影响; 图14为无人机x、y、z方向上的自主轨迹跟踪结果,结果表明在自主轨迹跟踪飞行中无人机平稳性总体较好,基本与仿真模拟结果趋于一致。综上所述,在面对微风环境干扰下无人机轨迹跟踪结果良好,并且对未知环境扰动也具有较强的鲁棒性。
表3 无人机起降位置偏差
Tab.3 UAV takeoff and landing position deviation cm
参数偏差参考值准心度0.531.03x向偏移0.972.00y向偏移2.912.00
表4 无人机控制参数响应结果
Tab.4 UAV control parameter response results s
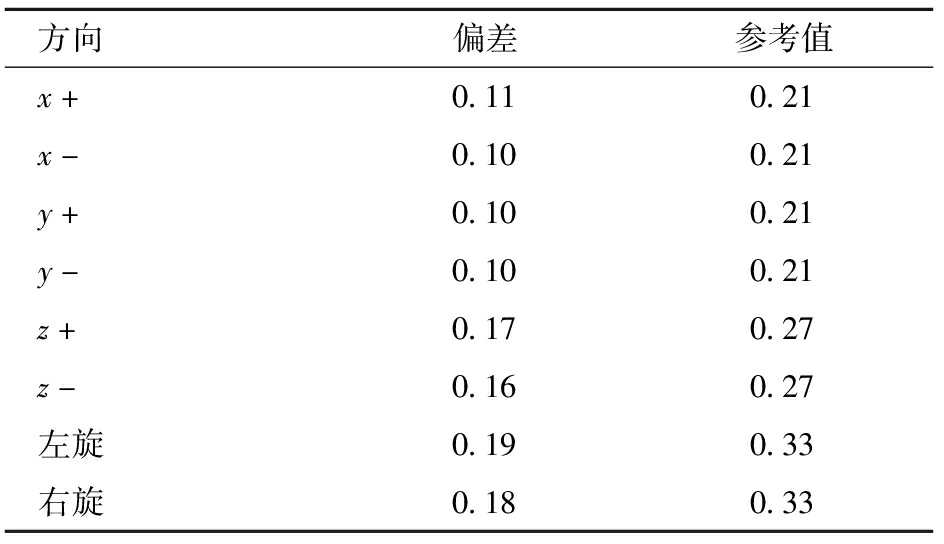
方向偏差参考值x+0.110.21x-0.100.21y+0.100.21y-0.100.21z+0.170.27z-0.160.27左旋0.190.33右旋0.180.33
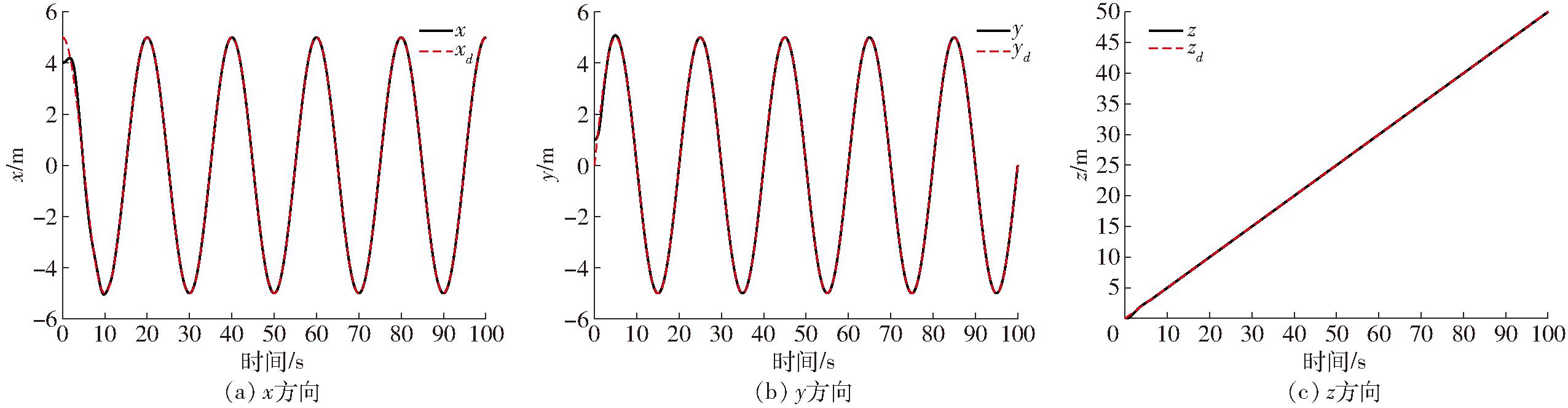
图14 无人机自主轨迹跟踪试验曲线
Fig.14 Experimental results of UAV trajectory tracking
提出了一种基于RBF神经网络的指定时间性能约束控制算法,针对具有参数不确定性和外部扰动的四旋翼飞行器,实现了在外界干扰下四旋翼无人机轨迹跟踪控制。与传统的反步法控制方案相比,所设计的控制器采用一阶滤波器避免了“参数爆炸”的问题,同时为了补偿所产生的滤波误差,采用一种新型的滤波补偿系统增强了系统稳定性。该控制算法采用的指定时间预设性能函数,可以保证四旋翼无人机轨迹跟踪误差在指定时间内快速收敛到零附近的邻域,增强了闭环系统鲁棒性。本文进行了控制策略的稳定性分析并证明了该闭环系统可以在指定时间内收敛。最后,在实际无人机飞行试验中,验证了所提出方法的有效性。
[1] 张立.基于串级PID控制算法的四旋翼无人机控制系统设计[J].信息技术与信息化,2023(1):100-103.
ZHANG Li.Design of quadrotor UAV control system based on serial PID control algorithm[J].Information Technology and Informatization,2023(1):100-103.(in Chinese)
[2] 陈丰毅,解明扬,张民,等.基于自适应神经网络的四旋翼无人机轨迹跟踪控制[J].控制工程,2023,30(7):1267-1275.
CHEN Fengyi,XIE Mingyang,ZHANG Min,et al.Trajectory tracking control of quadrotor UAV based on adaptive neural network[J].Control Engineering of China,2023,30(7):1267-1275.(in Chinese)
[3] 李鸿一,王琰,姚得银,等.基于事件触发机制的多四旋翼无人机鲁棒自适应滑模姿态控制[J].中国科学:信息科学,2023,53(1):66-80.
LI Hongyi,WANG Yan,YAO Deyin,et al.Robust adaptive sliding mode attitude control for multi-quadcopter UAVs based on event-triggered mechanism[J].Chinese Science:Information Science,2023,53(1):66-80.(in Chinese)
[4] 李一波,宋述锡.基于模糊自整定PID四旋翼无人机悬停控制[J].控制工程,2013,20(5):910-914.
LI Yibo,SONG Shuxi.Fuzzy self-tuning PID-based hovering control of quadrotor UAV[J].Control Engineering of China,2013,20(5):910-914.(in Chinese)
[5] 李成林,齐本胜,苗红霞,等.四旋翼串级自耦PID姿态控制器设计[J].自动化与仪器仪表,2023(2):103-106.
LI Chenglin,QI Bensheng,MIAO Hongxia,et al.Design of quadrotor serial autocoupled PID attitude controller[J].Automation and Instrumentation,2023(2):103-106.(in Chinese)
[6] 曹光乔,李亦白,南风,等.植保无人机飞控系统与航线规划研究进展分析[J].农业机械学报,2020,51(8):1-16.
CAO Guangqiao,LI Yibai,NAN Feng,et al.Analysis on the research progress of flight control system and route planning of plant protection UAV[J].Transactions of the Chinese Society for Agricultural Machinery,2020,51(8):1-16.(in Chinese)
[7] WANG F,GAO H,WANG K,et al.Disturbance observer-based finite-time control design for a quadrotor UAV with external disturbance[J].IEEE Transactions on Aerospace and Electronic Systems,2021,57(2):834-847.
[8] 郑潇,文颖,丁佳雨,等.饱和输入下四旋翼无人机滑模轨迹跟踪控制[J].计算机测量与控制,2023,31(1):86-92.
ZHENG Xiao,WEN Ying,DING Jiayu,et al.Sliding mode trajectory tracking control of a quadrotor UAV under saturated input[J].Computer Measurement and Control,2023,31(1):86-92.(in Chinese)
[9] 唐堂.四旋翼无人机姿态的自抗扰控制算法研究[D].南宁:广西师范大学,2018.
TANG Tang.Research on self-resilient control algorithm for quadrotor UAV attitude[D].Nanning:Guangxi Normal University,2018.(in Chinese)
[10] 王海荟,崔国增,李泽,等.四旋翼飞行器固定时间自适应轨迹跟踪控制[J].控制工程,2022,29(5):861-866.
WANG Haihui,CUI Guozeng,LI Ze,et al.Fixed-time adaptive trajectory tracking control for quadrotor[J].Control Engineering of China,2022,29(5):861-866.(in Chinese)
[11] TAN J,GUO S.Backstepping control with fixed-time prescribed performance for fixed wing UAV under model uncertainties and external disturbances[J].International Journal of Control,2022,95(4):934-951.
[12] 季晓明,文怀海.自适应神经网络四旋翼无人机有限时间轨迹跟踪控制[J].智能系统学报,2022,17(3):540-546.
JI Xiaoming,WEN Huaihai.Adaptive neural network quadrotor UAV finite time trajectory tracking control[J].Journal of Intelligent Systems,2022,17(3):540-546.(in Chinese)
[13] BECHLIOULIS C P,ROVITHAKIS G A.Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performance[J].IEEE Transactions on Automatic Control,2008,53(9):2090-2099.
[14] CUI G,YANG W,YU J,et al.Fixed-time prescribed performance adaptive trajectory tracking control for a QUAV[J].IEEE Transactions on Circuits and Systems Ⅱ:Express Briefs,2022,69(2):494-498.
[15] WU X,ZHENG W,ZHOU X,et al.Adaptive dynamic surface and sliding mode tracking control for uncertain QUAV with time-varying load and appointed-time prescribed performance[J].Journal of the Franklin Institute,2021,358(8):4178-4208.
[16] ZHANG W,SHAO X,ZHANG W,et al.Unknown input observer-based appointed-time funnel control for quadrotors[J].Aerospace Science and Technology,2022,126:107351.
[17] SHEN Z,LI F,CAO X,et al.Prescribed performance dynamic surface control for trajectory tracking of quadrotor UAV with uncertainties and input constraints[J].International Journal of Control,2021,94(11):2945-2955.
[18] SHAO X,ZHANG W,ZHANG W.Improved prescribed performance anti-disturbance control for quadrotors[J].Applied Mathematical Modelling,2021,97:501-521.
[19] RAZMI H,AFSHINFAR S.Neural network-based adaptive sliding mode control design for position and attitude control of a quadrotor UAV[J].Aerospace Science and Technology,2019,91:12-27.
[20] ZHANG Y,WU G,YANG X,et al.Appointed-time prescribed performance control for 6-DOF spacecraft rendezvous and docking operations under input saturation[J].Aerospace Science and Technology,2022,128:107744.
[21] SHI X,CHENG Y,YIN C,et al.Design of adaptive backstepping dynamic surface control method with RBF neural network for uncertain nonlinear system[J].Neurocomputing,2019,330:490-503.
[22] LIU K,WANG R,WANG X,et al.Anti-saturation adaptive finite-time neural network based fault-tolerant tracking control for a quadrotor UAV with external disturbances[J].Aerospace Science and Technology,2021,115:106790.
[23] ZHANG C,MA G,SUN Y,et al.Observer-based prescribed performance attitude control for flexible spacecraft with actuator saturation[J].ISA Transactions,2019,89:84-95.
[24] LIU H,ZHENG H,ZHANG Y,et al.Fixed-time self-structuring neuron network-based adjustable prescribed performance control for a quadrotor UAV with input saturation[J].IEEE Access,2023,12:2474-2489.