0 引言
随着新能源汽车的快速发展,轮毂电机技术也随之推广[1-2]。轮毂电机大多数基于传感器量测数据,采用PID、滑模变结构、模型预测等方法对电机转速和转矩进行控制[3-6]。轮毂电机转速和转矩控制主要受限于传感器精度,难以满足高精度和高动态响应等要求。近年来国内外诸多学者对电机控制进行了深入研究,取得了许多先进成果。无传感器控制方面,李勇等[7]利用fal函数构建变增益非线性自适应律,结合自抗扰算法,在宽转速范围、负载突变等复杂工况下能够准确估算轮毂电机转子位置;赵其进等[8]提出了在基速区采用弱磁和最大转矩电流比控制,在低速区注入脉振高频,在中高速区采用模型参考自适应方法的无位置传感器复合控制技术;唐辉等[9]提出提前注入信号相位并从两次高频响应电流的差值中辨识轮毂电机转子位置; PASQUALOTTO等[10]通过将EKF算法和神经网络算法结合,在处理同步磁阻电机磁饱和和非线性问题上取得了良好的效果。转速和转矩控制方面,宋战锋等[11]制定24种矢量电压合成方案,采用多级滞环的直接转矩控制策略,将转矩脉动和谐波电流控制在较低水平;郑长森等[12]将分数阶微积分算子与非奇异终端滑模结合,设计一种无模型分数阶非奇异终端滑模控制器;程启明等[13]引入复叠式超螺旋算法(CSSMC)对转速环进行控制,采用超螺旋滑模(STSMC)直接转矩控制;KIM等[14]设计一种鲁棒模型预测速度控制器,在参数不确定性和扰动存在时对永磁同步电机速度进行控制。本文将无传感器估计与电机转矩转速控制相结合,采用MCSRGHCKF估计算法,相比传统高阶卡尔曼算法,发挥最大相关熵(MCC)噪声适应性强和平方根原理迭代计算快的优势,使该算法能够在非高斯噪声下对轮毂电机转速和转子角度准确快速估计,并进一步开发基于积分滑模面的STSMC算法,对轮毂电机转速转矩进行控制,并通过仿真和实验验证控制效果。
1 轮毂电机汽车转速和转矩控制工况
后轮驱动轮毂电机汽车变道超车工况,变道时匀速行驶,变道后直线加速。变道时须符合阿克曼转向原理,确保整车稳定[15-16]。按图1计算后驱车轮转速[17],图中O为转向中心,G为车辆质心,v为车速,vrl、vrr为左、右后轮速度,r为车辆质心转向半径,rf、rr为左、右后轮转向半径,lf、lr为前、后轴距,b为左右轮距,r0为车轮半径。
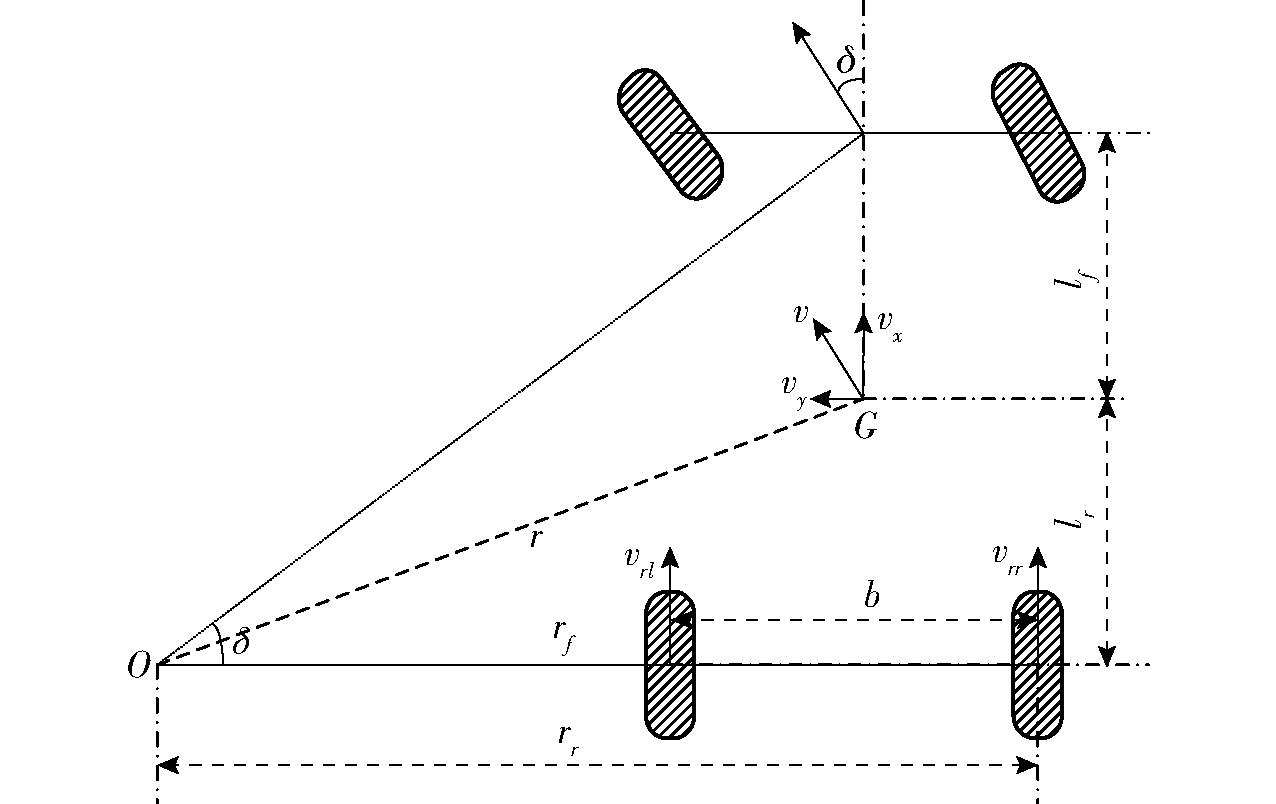
图1 后轮驱动的阿克曼转向原理图
Fig.1 Ackermann steering principle diagram for rear wheel drive
根据几何关系可得
(1)
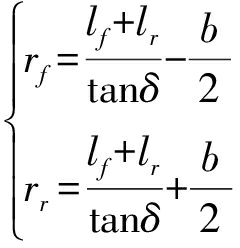
(2)
式中 δ——车辆转角
根据瞬心定理可得
(3)
假设车轮无滑移,可得
(4)
解得
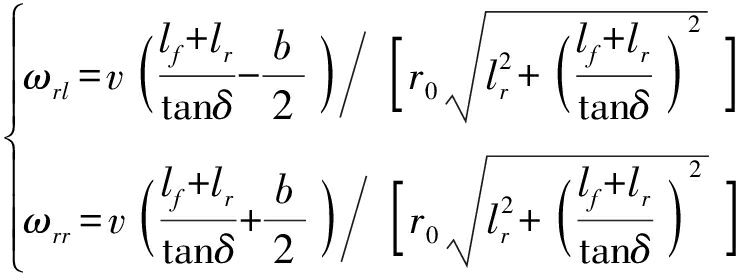
(5)
式中 ωrl、ωrr——左、右后轮转速
变道后轮毂电机汽车加速超车,为提高响应速度,直接对电机进行转矩控制[18]可得
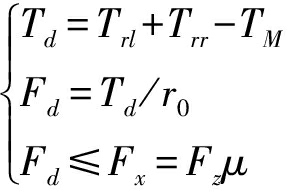
(6)
式中 Fd、Td——整车驱动力和力矩
Trl、Trr——左、右后轮毂电机输出转矩
TM——整车阻力矩
μ——路面附着系数
Fx——路面附着力
Fz——整车垂直载荷
在加速过程中Fd不能大于路面附着力Fx,否则车轮会打滑。根据车辆运动学计算的期望驱动力矩,按照最优分配准则分配到两后驱轮毂电机[19-21],计算后驱轮毂电机输出力矩,目标函数J为
(7)
式中 Fzrl、Fzrr——左、右后轮垂直载荷
μrl、μrr——左、右后轮路面附着系数
综上,当轮毂电机汽车进行变道超速时,可采用式(5)、(7)分别对轮毂电机进行转速和转矩控制。
2 轮毂电机转速和转矩控制
2.1 轮毂电机数学模型
轮毂电机为表贴式永磁同步电机,分别在旋转坐标系dq和静止坐标系αβ下建立轮毂电机数学模型[22]。
2.1.1 旋转坐标系dq下
轮毂电机定子电压方程为
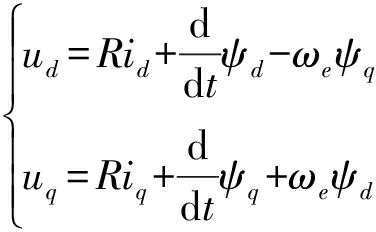
(8)
式中 R——定子电阻 ud、uq——d、q轴向电压
ψd、ψq——定子磁链d、q轴分量
ωe——电机点角速度
id、iq——d、q轴向电流
轮毂电机定子磁链方程为
(9)
式中 L——dq轴电感分量
ψf——永磁体磁链
轮毂电机电磁转矩方程为
Te=1.5pniqψf
(10)
式中 Te——轮毂电机电磁转矩
pn——电机磁极对数
电角度、电角速度与机械角度、机械角速度关系为
(11)
式中 θe——电机转子电角度
θm——电机转子机械角度
ωm——电机机械转速
将式(9)、(11)代入式(8)可得
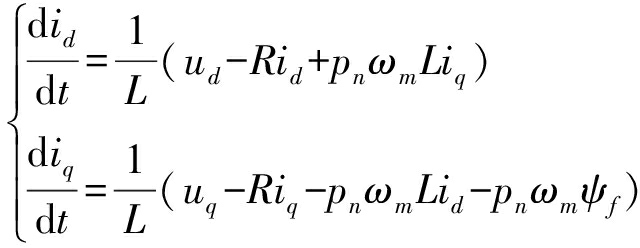
(12)
2.1.2 静止坐标系αβ下
对旋转坐标系dq下电压方程进行Park逆变换,得到轮毂电机在静止坐标系下电压电流关系式
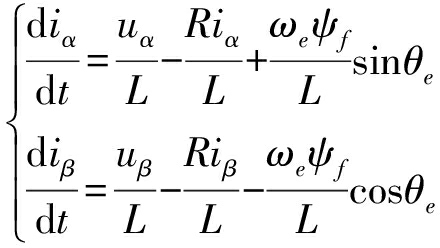
(13)
式中 iα、iβ——α、β轴向电流
uα、uβ——α、β轴向电压
轮毂电机动力学方程为
(14)
式中 TL——轮毂电机实际负载转矩
JW——电机转动惯量
Te——轮毂电机电磁转矩
轮毂电机电角度与转速关系为
(15)
2.2 轮毂电机转速和转矩控制原理
如图2所示,整车驱动力为TL,TR表示轮毂电机分配力矩Trl和Trr,ωR表示左右后轮转速ωrl和
为轮毂电机转速环向正弦过渡模块输出转矩,
为轮毂电机转速环向转矩环输入电流。电机采用矢量控制(Field-oriented control, FOC),控制过程中转速ωm和转子机械角度θm由MCSRGHCKF模块估计。转速和转矩环均采用STSMC算法,区别文献[23]中基于STSMC算法控制磁链实现对电机的直接转矩控制,本文转矩控制是在FOC框架下采用STSMC算法直接对转矩环(d、q轴电流)进行控制,具有无需计算磁链、转矩脉动小、精度高等特点。
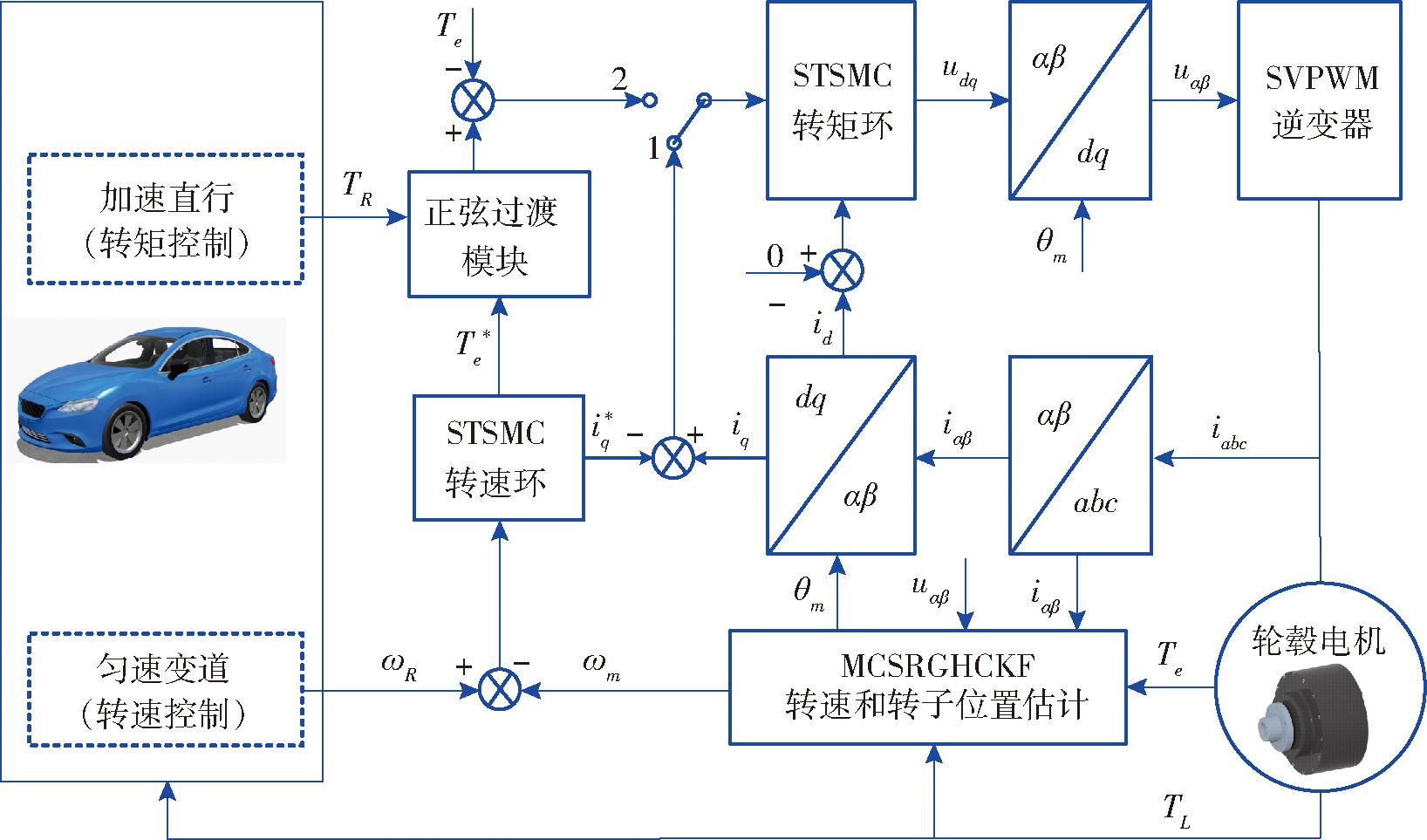
图2 轮毂电机转速和转矩控制原理图
Fig.2 Schematic of in-wheel motor speed and torque control
当轮毂电机汽车匀速变道运行,轮毂电机采用转速控制模式1;加速直行运行,采用转矩控制模式2,正弦过渡模块将转速控制模式时的转矩输出值
平滑过渡到轮毂电机分配力矩TR,保证电机三相电流iabc快速且渐进变化,防止其发生突变,对轮毂电机造成冲击,轮毂电机反馈电磁力矩Te与TR进行比较。
2.3 轮毂电机转速和转子角度估计器设计
由2.2节可知,转速和转矩控制都需实时反馈轮毂电机机械转速ωm和转子机械角度θm。对于风机、泵类等启动负载较小的场景,可直接采用无传感器控制。但轮毂电机为重载启动,电机很难自动获得角度和转速等初始值,只能依靠传感器测量。当轮毂电机汽车运行后,为防止传感器误差和故障,保证监测精度以及运行安全可靠,可采用无传感器估计方法获取转速和位置信息。最大相关熵准则(Maximum correntropy criterion, MCC)是处理复杂噪声的一种有效优化准则,在高效处理数据同时能够有效适应非高斯噪声[24]。而平方根广义高阶容积卡尔曼算法(Square root generalized high-order cubature Kalman filter, SRGHCKF)计算量小,迭代过程稳定,估计精度高[25]。两种算法相结合,设计MCSRGHCKF算法,可实现对启动后轮毂电机机械转速ωm和转子机械角度θm复杂噪声环境下的快速精确估计。
转速和转子角度估计器状态变量x=(iα, iβ, ωm, θm)T,量测变量z=(iα,iβ)T,输入变量u=(uα,uβ,Te,TL,iα,iβ),由式(13)～(15)可得转速和转子位置估计的状态方程和量测方程
(16)
其中
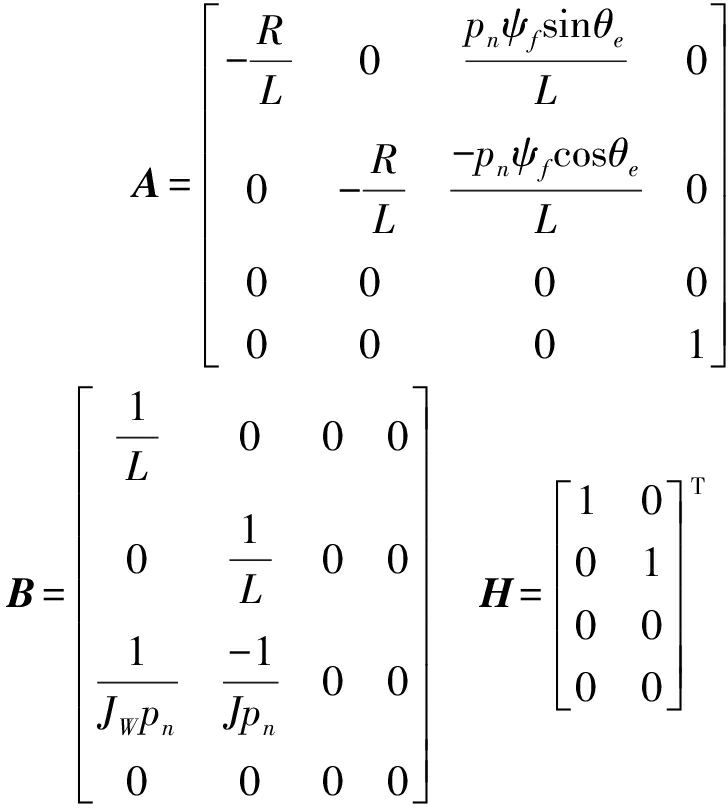
其中Q(t)、R(t)分别为系统过程噪声与量测噪声矩阵,且相互独立。
MCSRGHCKF算法估计流程如图3所示[26]。图中ζi为广义高阶容积卡尔曼的容积点,即
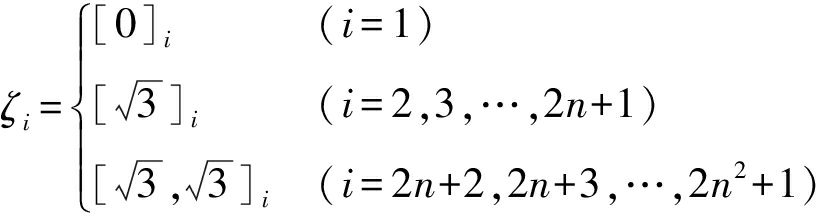
(17)
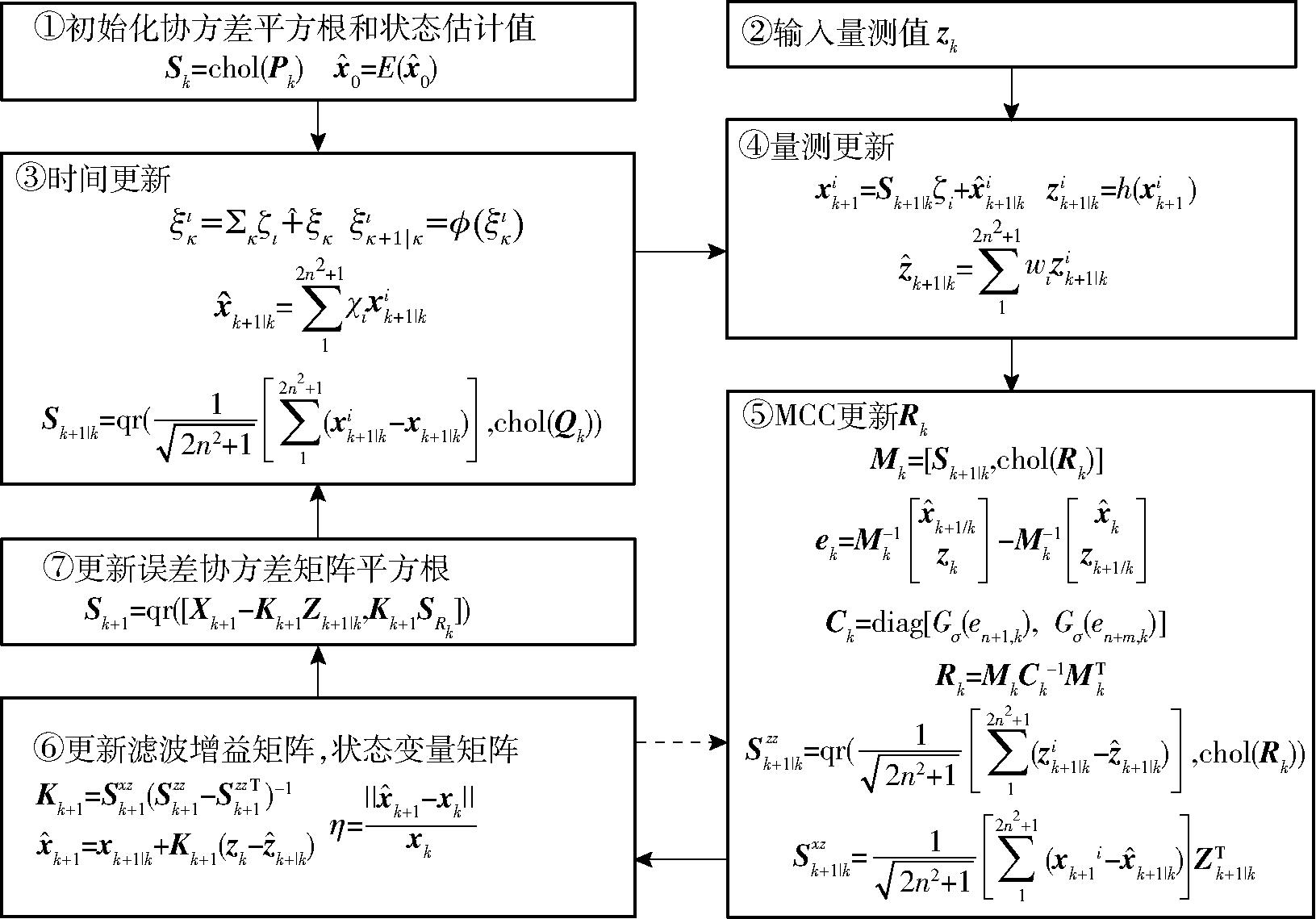
图3 轮毂电机转速和角度估计流程图
Fig.3 In-wheel motor speed and angle estimation process
χi为广义高阶容积卡尔曼权值,即
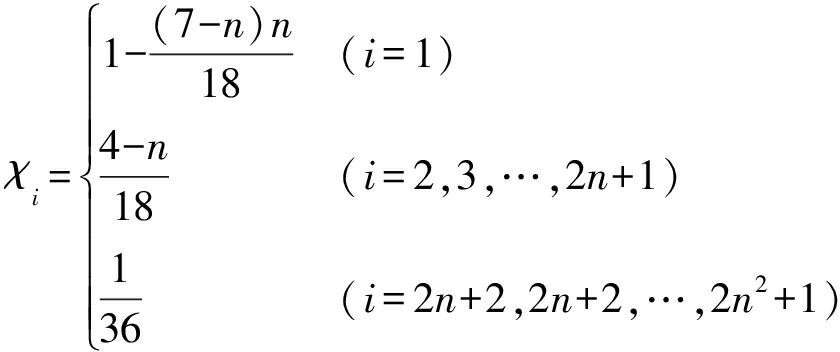
(18)
首先初始化协方差平方根和状态估计值,并对其进行时间更新,输入量测数据,更新量测值,然后采用MCC准则对量测噪声Rk更新后,再更新滤波增益矩阵和状态变量矩阵,并计算状态变化率η,计算式为
(19)
取极小值ε,如果η≥ε,循环图3中步骤⑤、⑥,期间不间断迭代状态矩阵xk,即
xk=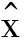
k+1
(20)
如果η<ε,则图3中步骤⑤、⑥循环结束,取最优解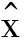k+1,继续完成本次估计流程。最后采用QR分解方式更新误差协方差矩阵平方根,进行下一次状态估计。
2.4 轮毂电机转速和转矩控制器设计
对比传统滑模控制算法,STSMC使用积分来获得实际控制量,不含高频切换量,使得系统中没有抖动,同时其控制变量及其导数能在有限时间内收敛,控制性能优越。
STSMC控制率[27]为
(21)
其中,k1、k2为控制率设计系数,s为滑模面。k1项包含切换量,其决定控制系统收敛速度和稳态误差,k2项包含切换量积分,其值影响系统稳态误差。
为减少STSMC控制过程中误差累积,设计积分滑模面
(22)
其中,系数c为滑模面斜率,其影响系统误差收敛速度,e为转矩误差或者电流误差。
证明STSMC控制算法的稳定性,构造李雅普诺夫函数
(23)
可知,V>0,对李雅普诺夫函数(23)求导,并将式(21)代入,得到
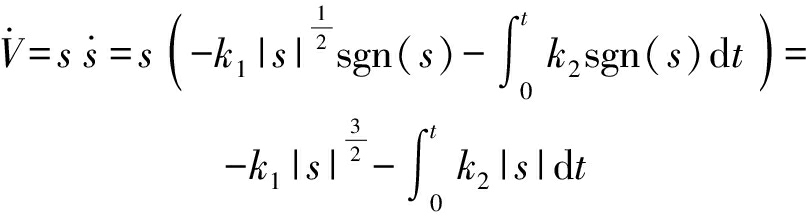
(24)
当满足
时,系统稳定,所以k1、k2取值大于0时,可得
(25)
可令k1>0且k2>0,STSMC控制算法符合李雅普诺夫第二稳定性定律,满足滑模可达性条件,系统在有限时间内渐进稳定。
2.4.1 轮毂电机转速控制模式
定义轮毂电机转速误差ev为
ev=ωR-ωm
(26)
对式(26)求导数,代入式(14)得
(27)
对积分滑模面式(22)求导,并代入式(21)、(27),得到转速环输出转矩为
Jpncev+TL
(28)
代入式(10)可得转速环输出电流为
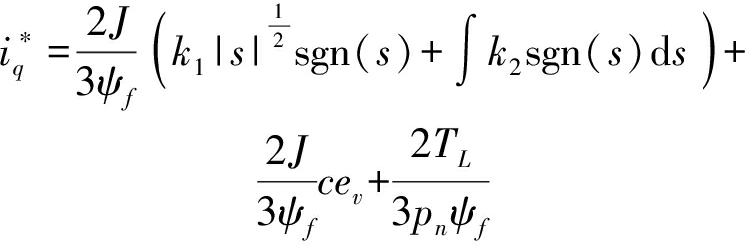
(29)
转速模式下继续对转矩环q轴和d轴电流进行控制,FOC控制算法解耦d-q轴电流后,需要控制d轴电流为0,如图2所示。分别定义q轴转矩误差eq和d轴电流误差ed为
(30)
式中
轴期望电流,取0
STSMC控制q轴和d轴电流,对式(22)、(30)求导,代入式(12)、(21)可得
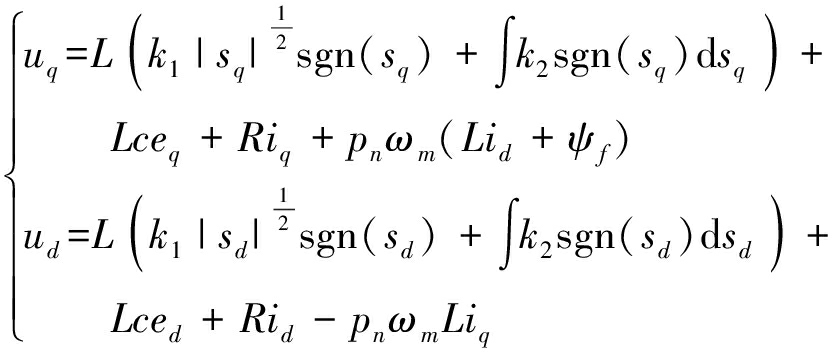
(31)
2.4.2 轮毂电机转矩控制模式
为提高响应速度,转矩模式时转速环不参与控制,由轮毂电机直接反馈电磁转矩Te,d轴电流控制方式不变,输出仍为式(31)中ud,而q轴电流控制量由转矩量取代,转矩误差eT为
eT=TR-Te
(32)
对式(22)、(32)求导,并代入式(10)、(21)、(31)中,uq更新为
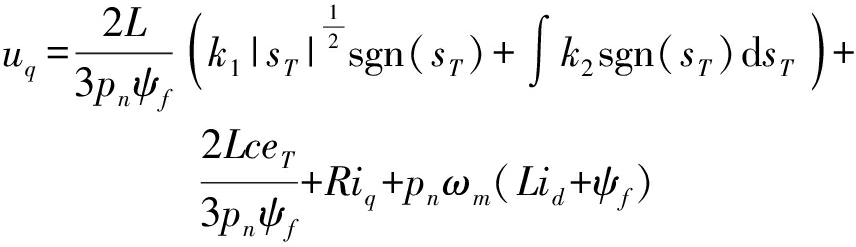
(33)
在控制模式切换瞬间,当轮毂电机分配转矩TR与转速环输出转矩
式(28))相差较大时,电机电磁转矩Te将发生跳变,三相电流也会发生跳变,导致电机运行不稳定,可在转速控制向转矩控制切换的过程中设计一种平滑性好的正弦函数过渡算法。
计算轮毂电机分配转矩TR与转速控制输出转矩差值为
(34)
设转速控制切换转矩控制时刻为t0,过渡时间为Δt,则转矩环过渡转矩Tt为
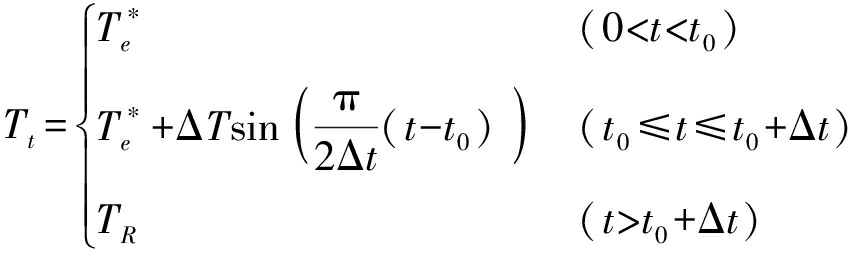
(35)
则式(32)改写为
eT=Tt-Te
(36)
3 仿真
搭建电机Simulink模型,结合整车Carsim模型对轮毂电机汽车单移线工况联合仿真,首先估计轮毂电机转速和角度,再对整车运行过程转矩和转速控制进行分析。设置车辆初始速度65 km/h,路面附着系数0.8,其余参数如表1所示。
表1 仿真参数
Tab.1 Simulation parameters
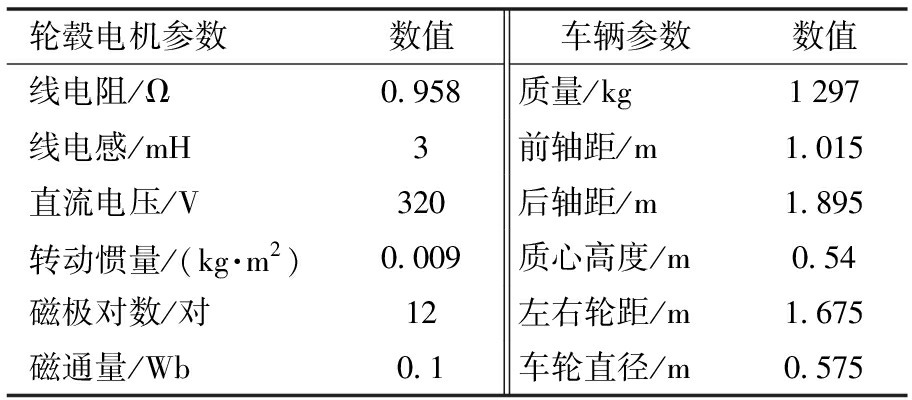
轮毂电机参数数值车辆参数数值线电阻/Ω0.958质量/kg1297线电感/mH3前轴距/m1.015直流电压/V320后轴距/m1.895转动惯量/(kg·m2)0.009质心高度/m0.54磁极对数/对12左右轮距/m1.675磁通量/Wb0.1车轮直径/m0.575
3.1 轮毂电机转速和转子角度估计仿真
由于传感器测量噪声对估计结果影响较大,在估计算法中对量测变量噪声R(t)矩阵进行更新。采用满足混合高斯分布的厚尾非高斯噪声
量测变量噪声R(t)=diag[0.019 0.028],初始化过程噪声Q(t)=diag[0.02 0.02 0.02 0.02],根据车速和车轮半径确定电机转速600 r/min,为体现MCSRGHCKF算法的先进性,分别采用GHCKF、SRGHCKF算法进行对比。
对比仿真结果,3种算法都能够估计轮毂电机转子转速和角度,如图4、5所示。分析转子角度估计误差,图6中轮毂电机转子电角度共运行10个周期,除第6周期和第9周期外,MCSRGHCKF估计结果均能够与其余电角度周期同步,估计误差为0,而SRGHCKF和GHCKF算法在所有电角度周期均无法同步,SRGHCKF算法估计误差为0.2 rad,GHCKF算法估计误差为0.6～0.8 rad,滤波效果方面,MCSRGHCKF和SRGHCKF算法转子位置曲线比GHCKF算法估计曲线平滑,效果明显。图7为轮毂电机转速误差,MCSRGHCKF算法估计误差为0,SRGHCKF算法估计误差为-0.2 r/min左右,GHCKF算法估计误差为-1～0.2 r/min,误差变化绝对值约为1.2 r/min。对比仿真曲线, MCSRGHCKF估计值和SRGHCKF估计值波动小,曲线平滑,两种算法的滤波效果也是明显优于GHCKF算法。
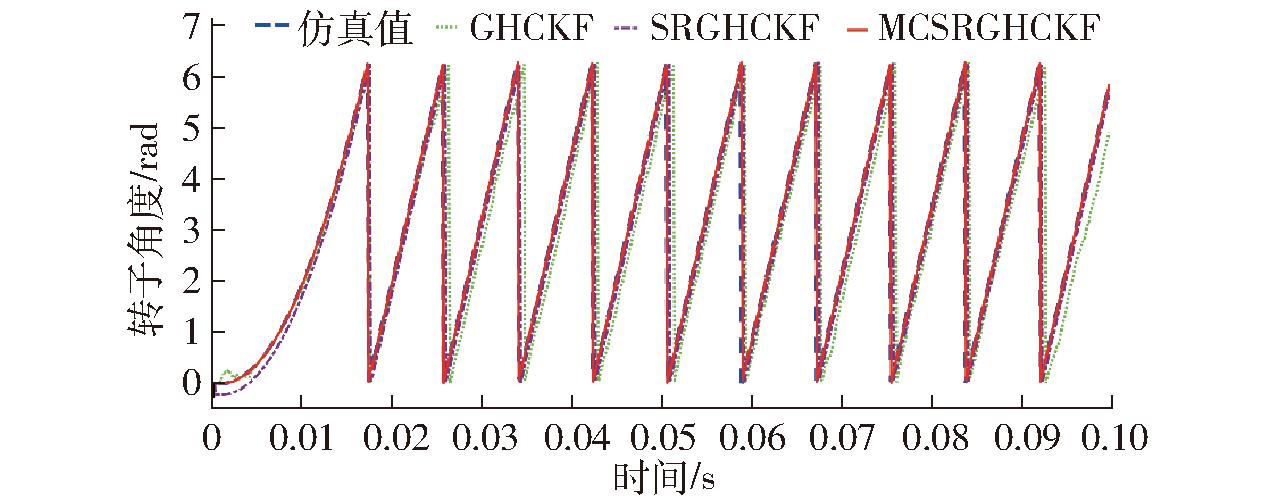
图4 轮毂电机转子角度估计
Fig.4 In-wheel motor rotor angle estimation
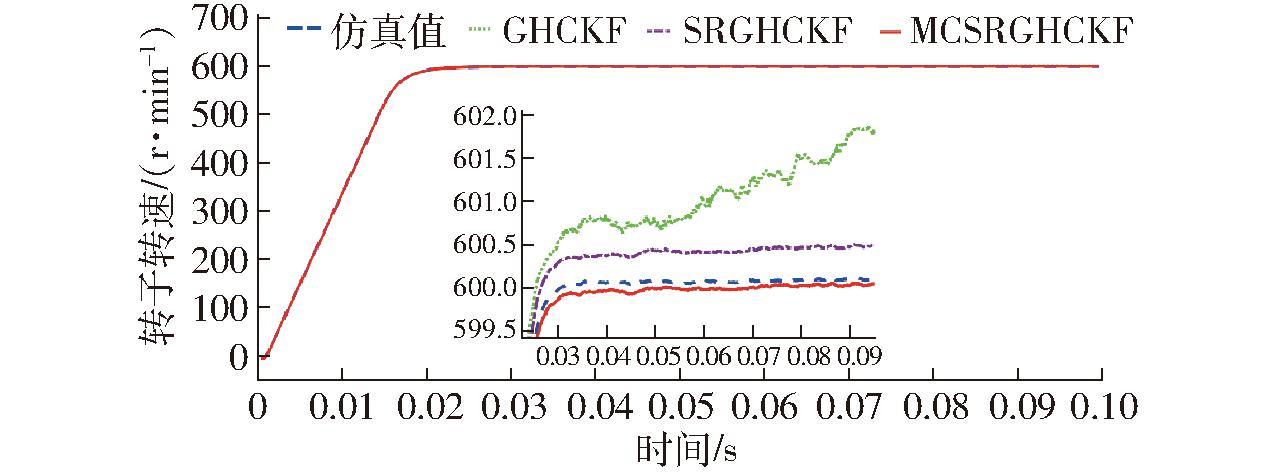
图5 轮毂电机转速估计
Fig.5 In-wheel motor rotor speed estimation
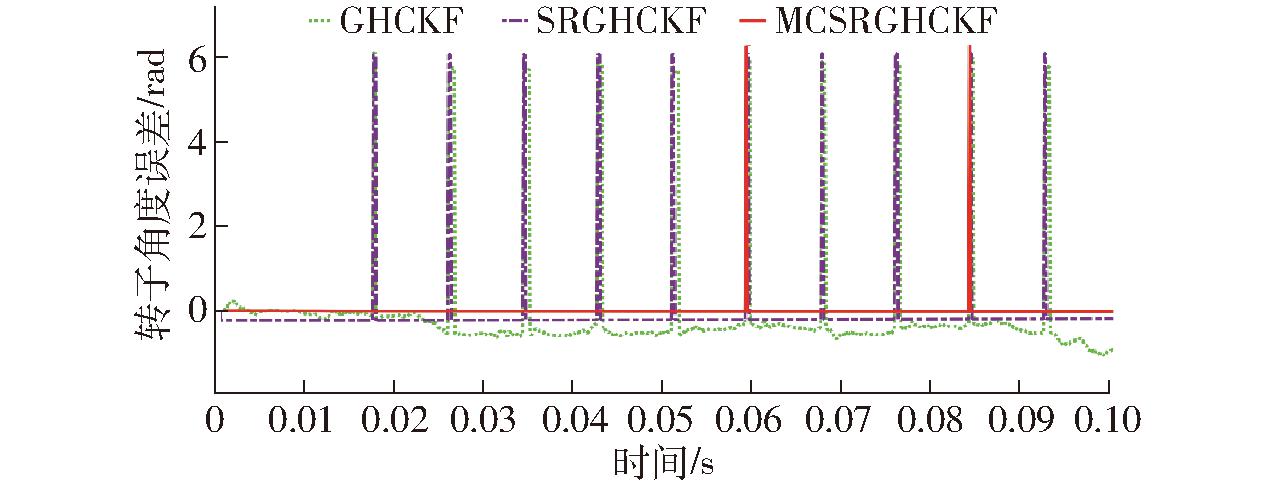
图6 轮毂电机转子角度误差
Fig.6 Angle error of in-wheel motor rotor
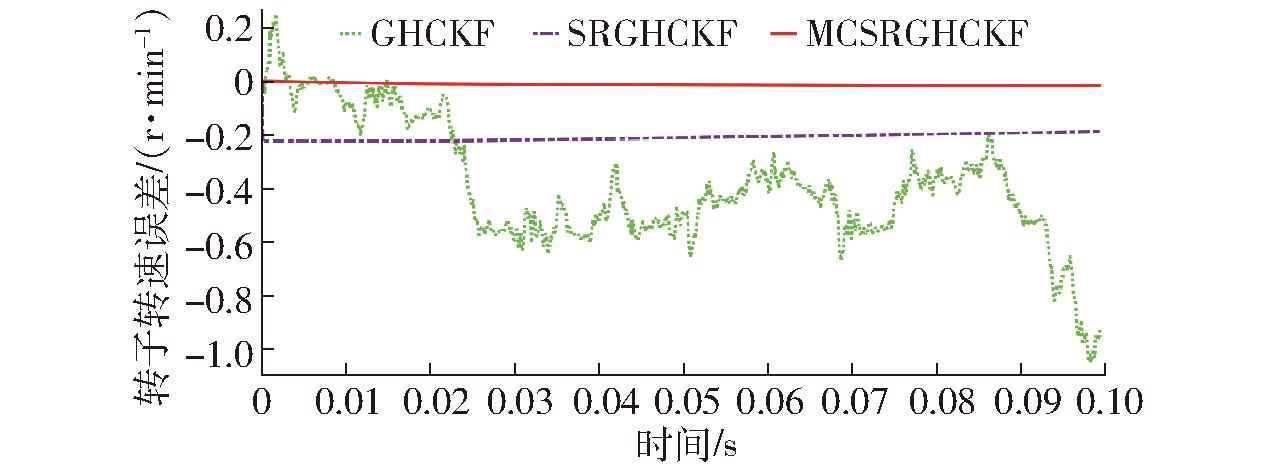
图7 轮毂电机转速误差
Fig.7 Speed error of in-wheel motor rotor
对比转子位置和转速估计精度和滤波效果,MCSRGHCKF算法估计效果最佳,鲁棒性最优,SRGHCKF算法次之,GHCKF算法估计效果最差。
3.2 轮毂电机转速转矩控制仿真
对轮毂电机汽车单移线工况进行仿真,如图8所示,在前50 m整车以速度65 km/h匀速变道,采用转速控制模式,变道宽度为3.5 m,匀速直线行驶30 m后,在纵向10 m内完成变道,再匀速行驶10 m后轮毂电机切换为转矩控制模式,后50 m整车直线加速。
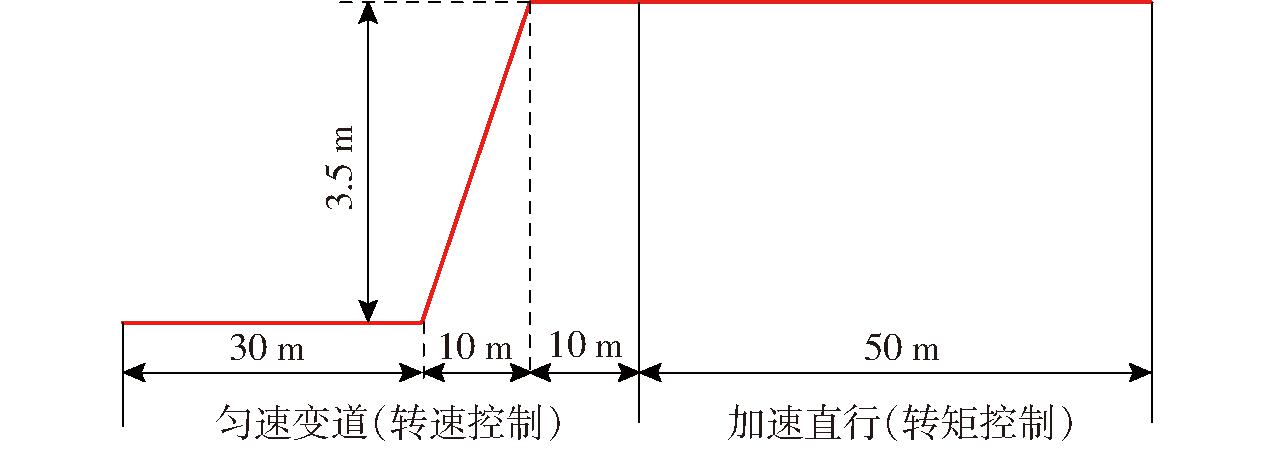
图8 单移线工况示意图
Fig.8 Schematic of single-lane change
为验证STSMC控制算法优越性,分别采用PID、指数趋近律SMC控制算法进行对比。如图9、10所示,低速高附着路面下,车辆未打滑,左右轮毂电机转矩输出基本一致,由放大图可知,转向时左侧车轮转矩波动值大于右侧车轮值1～3 N·m,输出滞后0.05～0.1 s。4.5 s之前左右轮毂电机为转速控制模式,4.5 s之后为转矩控制模式。转速控制模式下,车辆匀速行驶,转矩输出为30 N·m,转向变道时,转矩稳定变化,采用PID、SMC、STSMC算法控制的转矩脉动分别为±5 N·m、±4 N·m、±2 N·m,稳态误差分别为±16.7%、±13.3%、±6.7%;转矩控制模式下,转矩恒定输出105 N·m,采用PID、SMC、STSMC控制算法转矩脉动分别为±6 N·m、±3.5 N·m、±3 N·m,稳态误差分别为±5.7%、±3.3%、±2.9%。在4.5 s转速切换转矩模式时,3种算法控制下转矩均在0.01 s内从30 N·m跳变至105 N·m,SMC和STSMC算法在切换过程中转矩发生了振荡,这是由于滑模控制时高频切换变量导致,STSMC算法振荡明显小于SMC算法,证明了STSMC积分控制率的稳定性。
图9 左后轮毂电机输出转矩
Fig.9 Output torque of left rear in-wheel motor
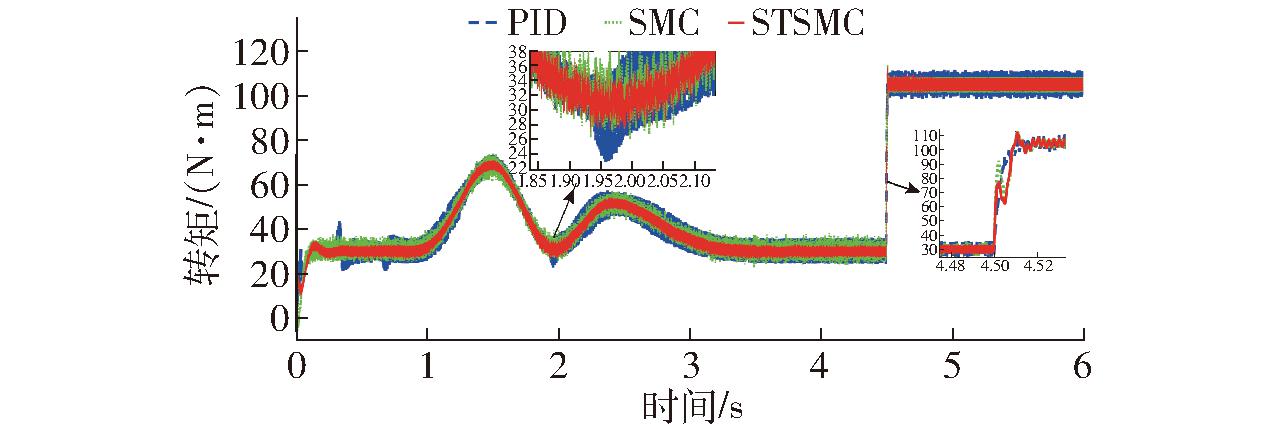
图10 右后轮毂电机输出转矩
Fig.10 Output torque of right rear in-wheel motor
如图11、12所示,4.5 s之前,轮毂电机汽车匀速变道,左右轮毂变化趋势相反,符合阿克曼转向原理。4.5 s后整车加速直行,两侧轮毂电机输出转速一致。当车速为65 km/h时,车轮转速基本维持在600 r/min,根据局部放大图,采用PID、SMC、STSMC算法转速脉动分别为±0.04 r/min、±0.025 r/min、±0.015 r/min,稳态误差分别为±0.007%、±0.004%、±0.002 5%。在4.5 s转矩切换转速时,左右轮毂电机由于转矩发生突变,左右轮速也从600 r/min瞬时跳变至602 r/min,然后以加速度 0.36 m/s2加速直行。
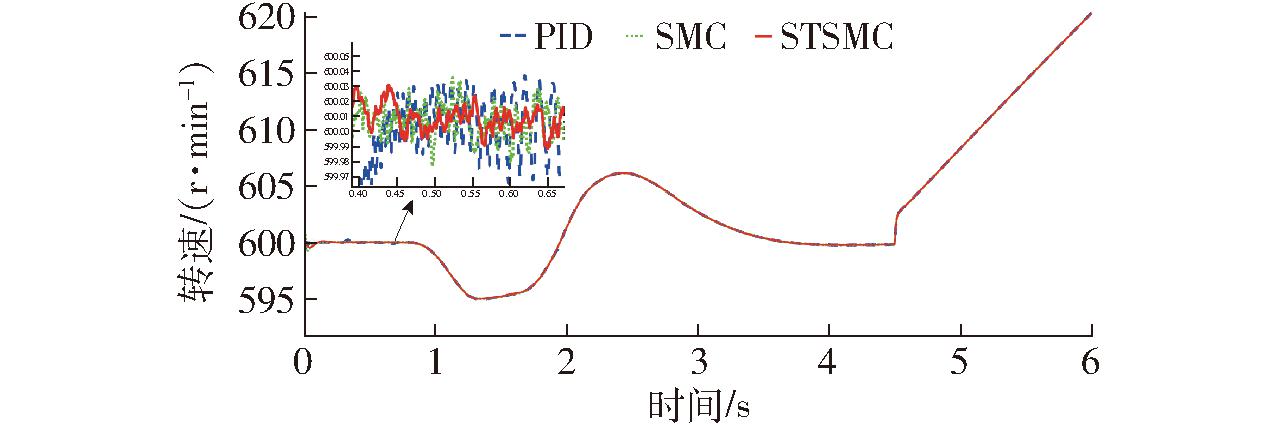
图11 左后轮毂电机输出转速
Fig.11 Output speed of left rear in-wheel motor
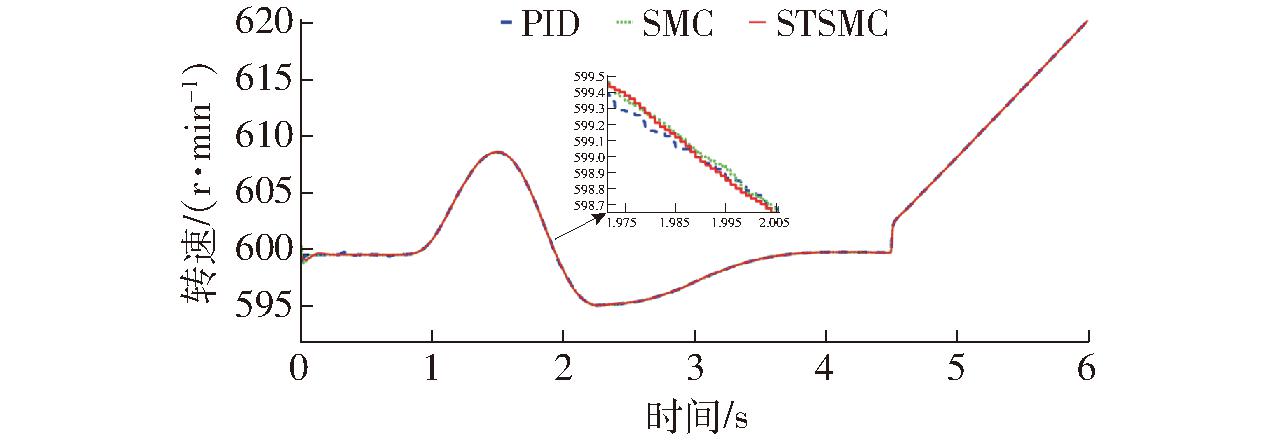
图12 右后轮毂电机输出转速
Fig.12 Output speed of right rear in-wheel motor
对比PID算法,STSMC和SMC算法转速和转矩脉动较小,控制精度高,间接证明了设计的积分滑模面(式(22))有效且先进。进一步对比,STSMC算法在转矩控制精度上又明显优于SMC算法,体现STSMC控制率优越性。
分析正弦过渡算法的转矩切换效果,如图13所示,采用正弦过渡函数,转速环输出转矩
能在0.5 s内平滑过渡到电机分配转矩TR,未发生无过渡控制下的转矩突变。图14中对比整车加速度,采用正弦过渡控制后加速度从0逐渐过渡到0.36 m/s2,同时单侧轮毂电机驱动电流也快速渐进过渡,如图15所示,有效避免了瞬时切换时电流发生突变,保证轮毂电机控制模式切换过程中稳定安全运行。
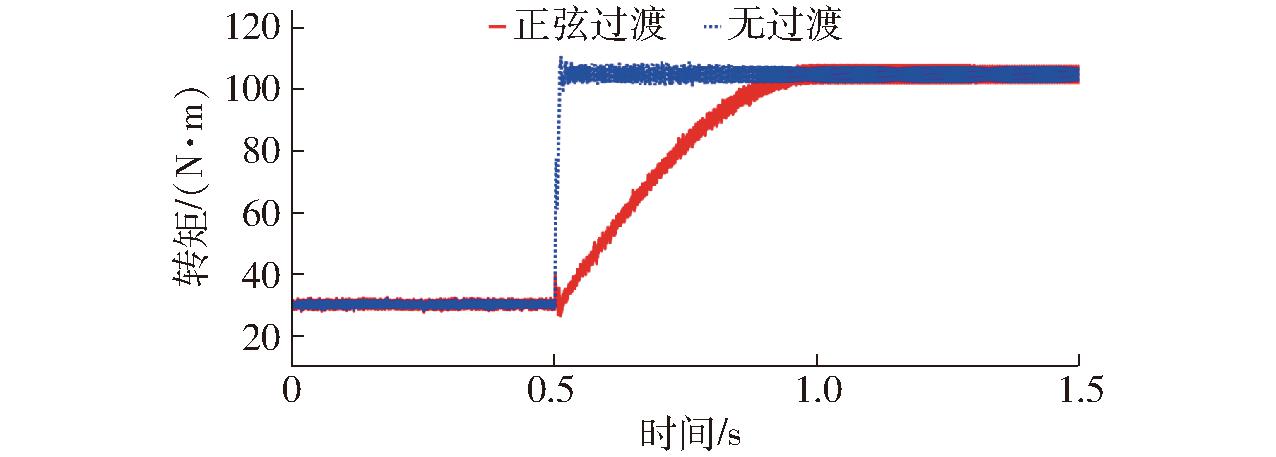
图13 正弦过渡转矩输出曲线
Fig.13 Sinusoidal transition torque output
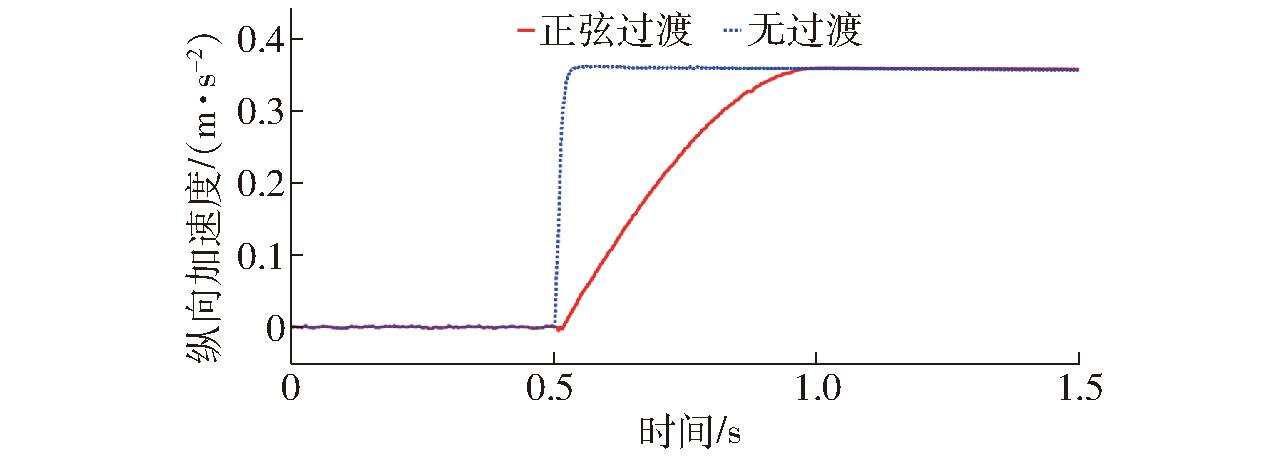
图14 正弦过渡整车加速度变化曲线
Fig.14 Acceleration change of whole vehicle during sinusoidal transition
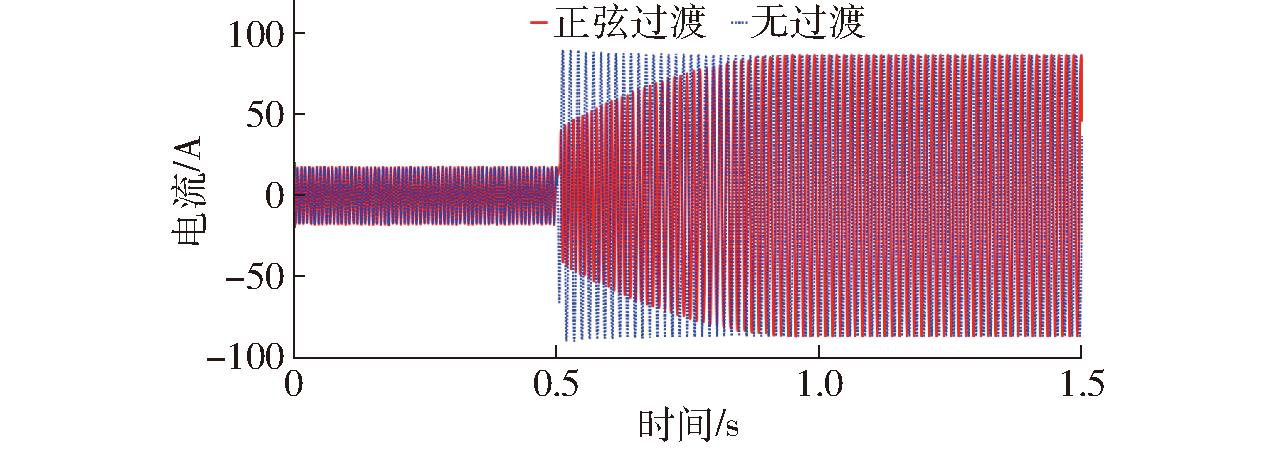
图15 正弦过渡电流输出曲线
Fig.15 Sinusoidal transition current output
4 实验
研究轮毂电机状态和输出特性,采集电机参数较多,很难在实车系统完成实验,本文利用永磁同步电机对拖平台验证电机MCSRGHCKF转速和角度估计算法,进一步对单电机转速和转矩控制进行实验,如图16所示,该平台基于TMS320F28335浮点数DSP处理器开发,控制精度高,采用最多支持10通道数据的实时显示的上位机软件,将开发的Simulink模型导入上位机,转换可执行C语言代码,编译后驱动42JSF630AS-1000型永磁同步电机运行,参数如表2所示。
表2 永磁同步电机参数
Tab.2 Parameters of permanent magnet synchronous motor
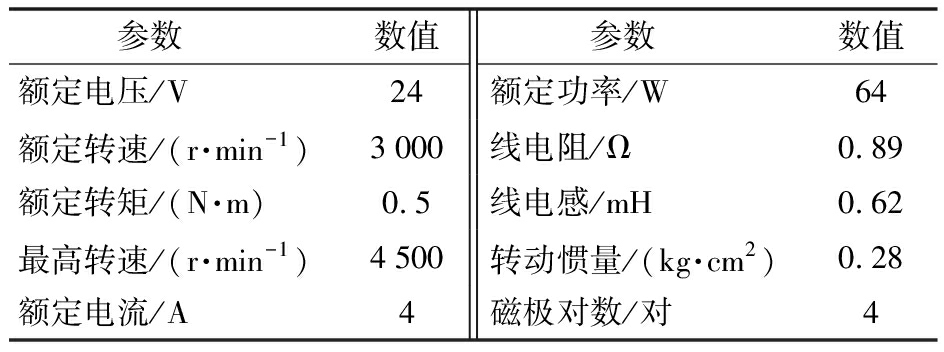
参数数值 参数数值额定电压/V24额定功率/W64额定转速/(r·min-1)3000线电阻/Ω0.89额定转矩/(N·m)0.5线电感/mH0.62最高转速/(r·min-1)4500转动惯量/(kg·cm2)0.28额定电流/A4磁极对数/对4
图16 永磁同步电机对拖实验平台
Fig.16 Permanent magnet synchronous motor towing platform
对拖电机采用直流无刷电机,额定扭矩0.65 N·m,转矩由WTQ1050D型动态微型扭矩传感器采集,量程为0～0.5 N·m。由转矩和转速仿真可知,轮毂电机在匀速变道过程中,转速为590～610 r/min,变化率不超过1.6%,可视为匀速,转矩负载约为30 N·m,加速过程中轮毂电机分配输出转矩105 N·m。实验电机额定转矩为0.5 N·m,实验转矩根据仿真数据300倍等比例缩放,实验中匀速阶段保持电机转速600 r/min,负载转矩设置为0.1 N·m,加速阶段期望电磁转矩设置为0.35 N·m。
4.1 电机转速和转子角度估计实验
电机从启动到转速恒定600 r/min,采集电机参数,代入到转子转速和角度估计器,对比GHCKF、SRGHCKF、MCSRGHCKF算法对电机转速和转子角度估计效果,如图17～20所示。
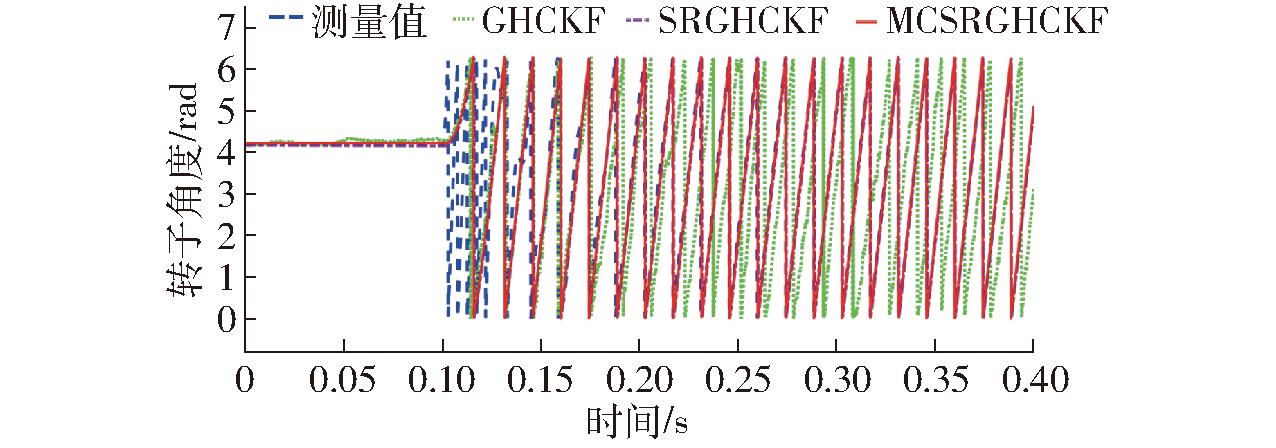
图17 转子角度估计
Fig.17 Rotor angle estimation
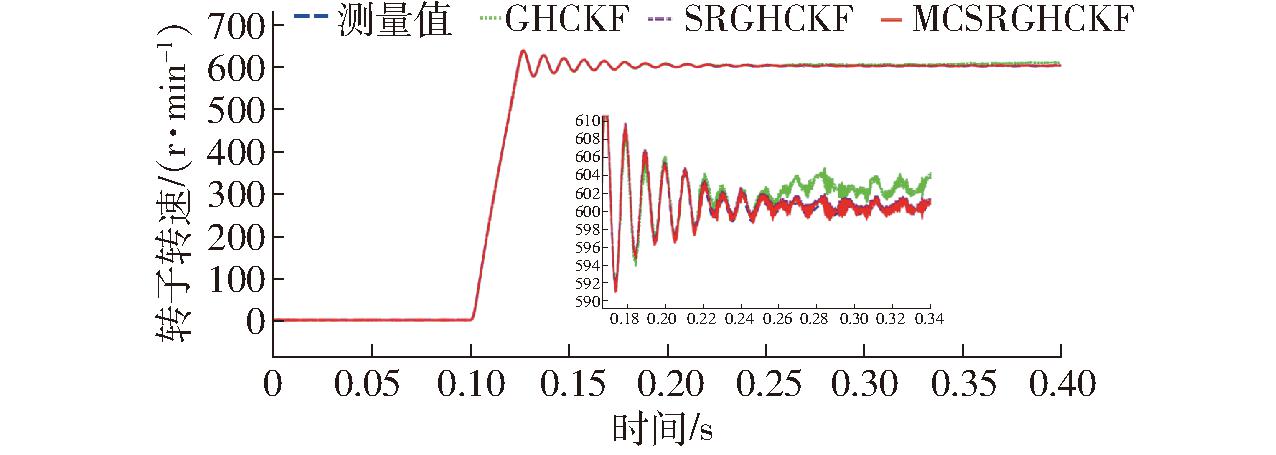
图18 转子转速估计
Fig.18 Rotor speed estimation
由图17、18可知,0.15 s之前,实验电机在0.1 N·m的对拖负载下启动,不同算法对转子转速估计值有效,但无法准确跟踪转子角度,与2.3节分析相符,即轮毂电机启动负载大,无传感器估计无法获得初始状态参数,启动阶段需传感器提供转速和角度信息,才能顺利平稳启动;0.15 s后,实验电机趋于稳定,GHCKF算法仍然无法准确估计电机的转子转速和角度,估计值误差较大甚至出现无效数据,而SRGHCKF和MCSRGHCKF算法可以有效估计电机转子转速和位置。分析转子位置估计误差,如图19所示,0.15 s后转子转过18个电角度周期,SRGHCKF算法均未实现任何一个周期同步估计,MCSRGHCKF算法可同步跟踪4个电角度周期,即第11～14电角度周期。由局部放大图可知,MCSRGHCKF、SRGHCKF算法转子角度估计误差分别为-0.05 rad和-0.15 rad。如图20所示,分析转速估计误差,MCSRGHCKF算法转速估计误差均集中在0.3 r/min,SRGHCKF算法转速估计误差约为0.5 r/min,前者转速估计精度明显高于后者。
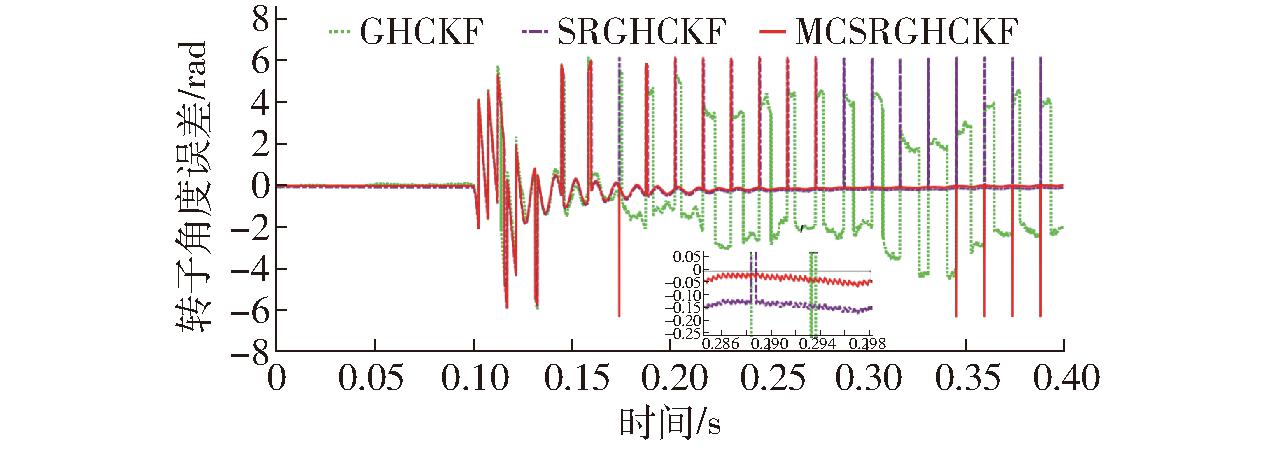
图19 转子角度误差
Fig.19 Rotor angle error
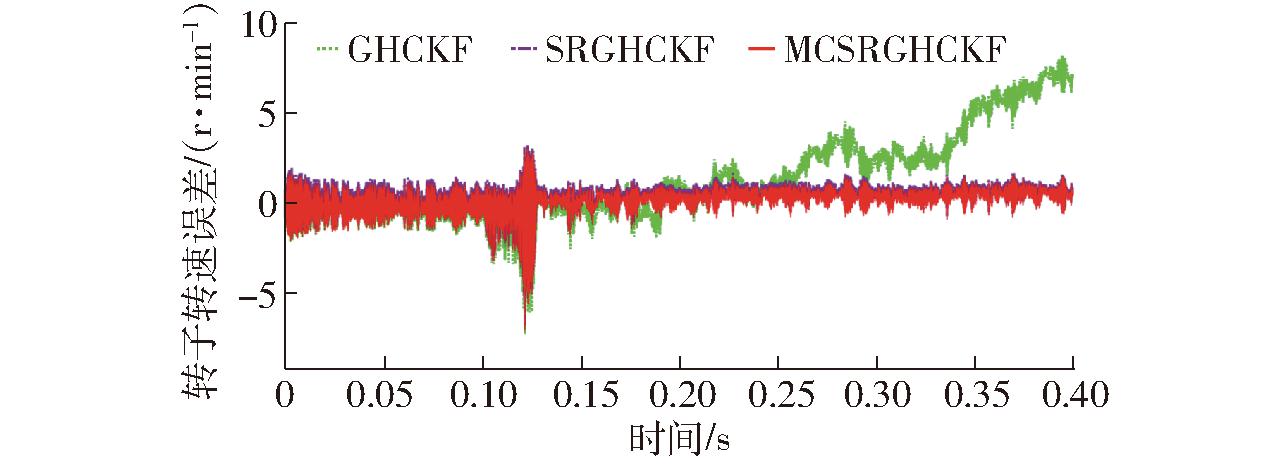
图20 转子转速误差
Fig.20 Rotor speed error
在电机稳定运行时,MCSRGHCKF算法能够准确估计实验电机转速和转子角度,具有较强的鲁棒性,SRGHCKF也可以实现电机转速和转子位置的在线估计,但是精度稍差。相比以上两种算法,GHCKF算法鲁棒性差,估计数据误差大,不具备实际应用价值。实验结果与仿真结果相一致,MCSRGHCKF算法具有先进性。
4.2 电机转速转矩控制实验
对电机转速转矩控制展开实验,图21、22分别为转速控制模式电机从启动到稳定时转速和转矩变化。从启动到匀速运行,STSMC算法最大启动转速为638 r/min,最大超调量为6.33%,最大启动转矩为0.35 N·m,是稳态转矩的3.5倍,约0.22 s后稳定运行;SMC算法最大启动转速为640 r/min,最大超调量为6.67%,最大启动转矩为0.35 N·m,是稳态转矩的3.5倍,约0.24 s后稳定运行;PID转速控制算法的最大启动转速达到680 r/min,最大超调量13.33%,启动最大转矩为0.45 N·m,是稳态转矩的4.5倍,约0.26 s后稳定运行。稳定后STSMC控制算法转速脉动为±0.5 r/min,转矩脉动为±0.01 N·m,SMC控制算法转速脉动为±1.5 r/min,转矩脉动为±0.015 N·m,PID控制算法转速脉动为±2 r/min,转矩脉动为±0.005 N·m。可知,转速控制时,STSMC转速控制算法除转矩脉动指标稍大于PID算法,其余指标均优于SMC和PID转速控制算法。
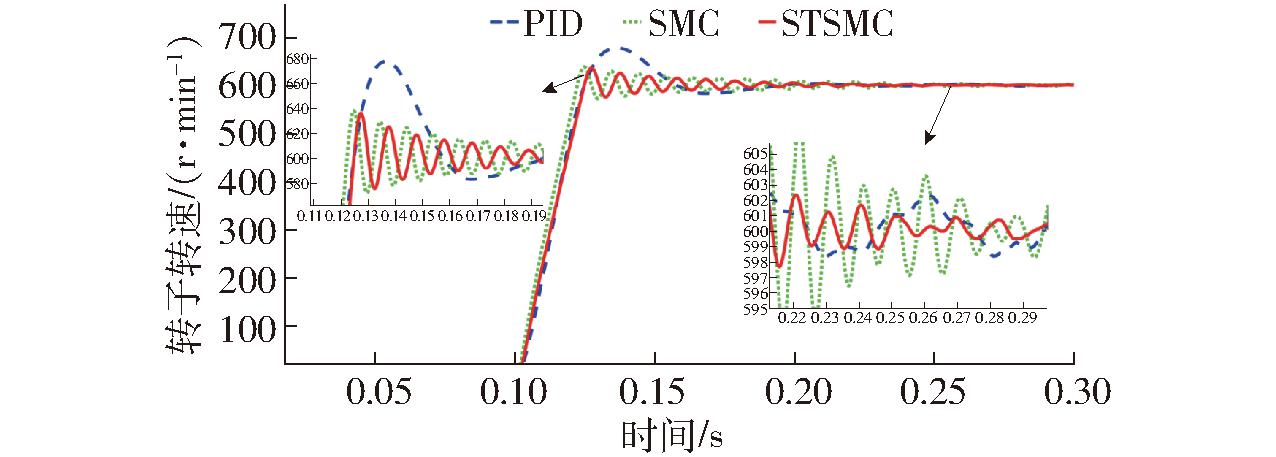
图21 转速控制模式转速
Fig.21 Speed in speed control mode
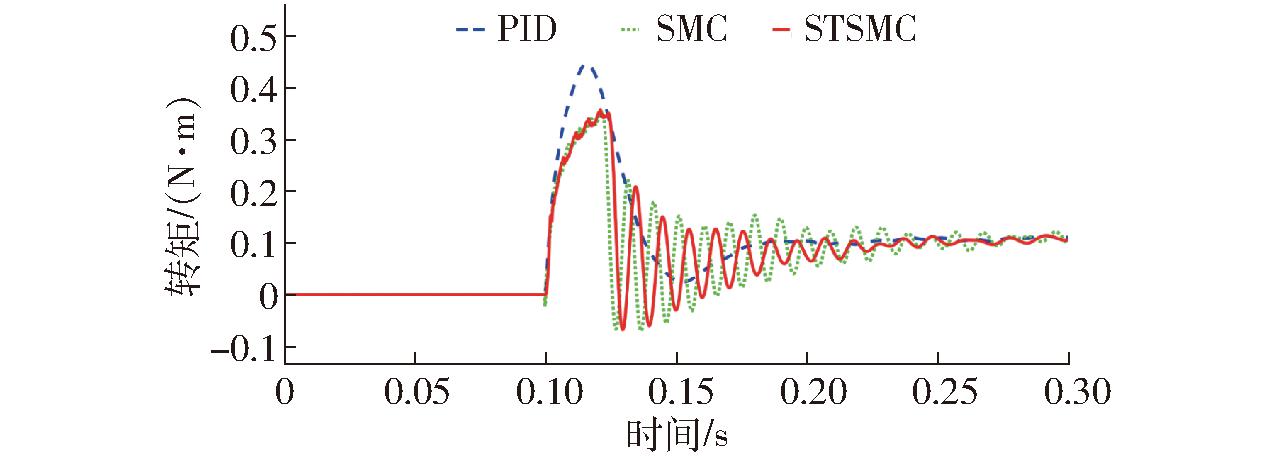
图22 转速控制模式转矩
Fig.22 Torque in speed control mode
实验电机匀速运行0.1 s后,开始模拟轮毂电机直线加速工况。如图23所示,实验电机切换为转矩控制模式,STSMC和SMC转矩控制算法瞬时最大转矩输出约为0.36 N·m,超调2.86%,STSMC算法控制转矩脉动明显小于SMC算法。PID控制算法瞬时最大转矩输出约为0.5 N·m,超调42.86%,对比数据可知,STSMC算法在转矩控制时,控制精度最高,滤波效果最佳。
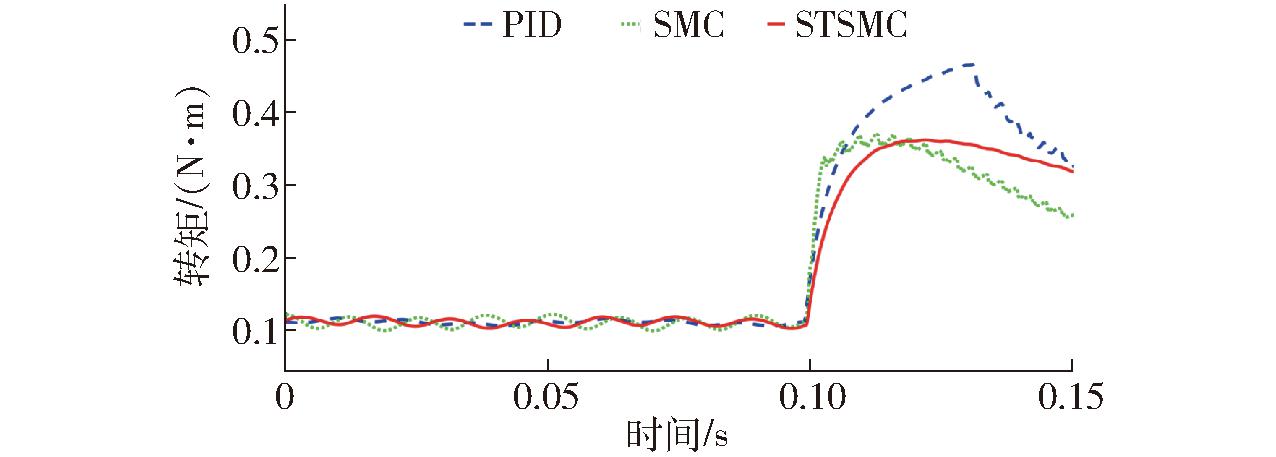
图23 转矩控制模式转矩对比
Fig.23 Torque comparison in torque control mode
如图24、25所示,对比转矩切换过程中采用正弦过渡控制策略后的效果。采用正弦曲线过渡方式后,电机的转矩输出在0.02 s内由0.1 N·m平滑上升到 0.36 N·m,对应三相电流输出在0.02 s内由 ±0.05 A 渐进变化为±0.19 A。电机控制模式直接切换时,电机转矩输出由0.1 N·m瞬间上升到 0.36 N·m,对应三相电流输出由±0.05 A突变为 ±0.27 A,电机出现异响。对比可知,正弦曲线过渡能使电机平稳运行,具有应用价值。
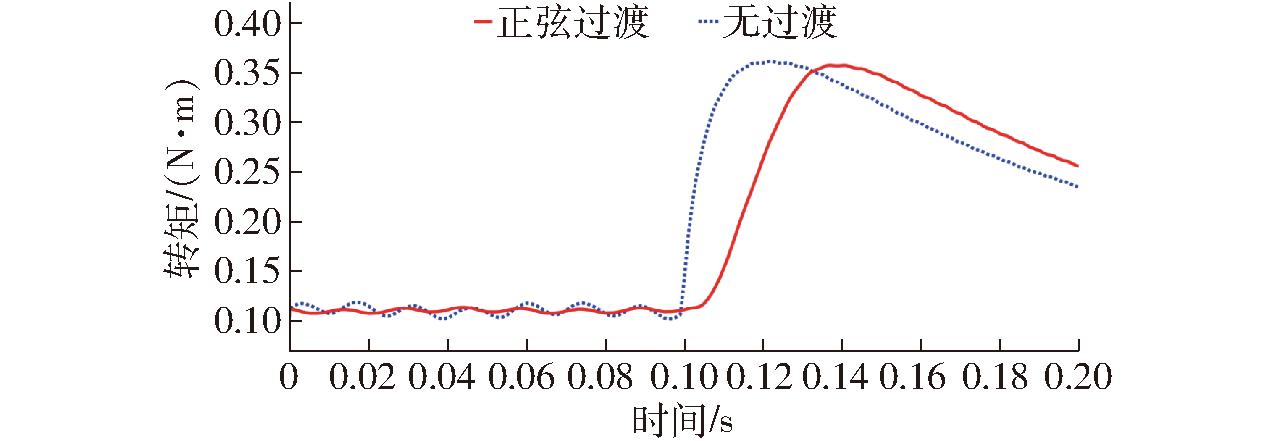
图24 过渡状态下转矩对比
Fig.24 Comparison of torque in transition state
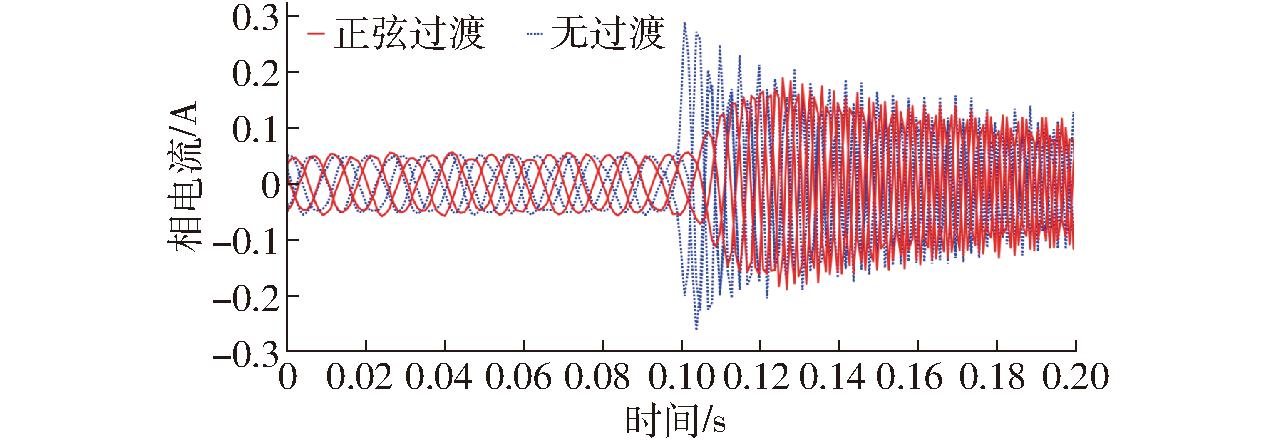
图25 过渡状态下电流对比
Fig.25 Comparison of current in transition state
5 结论
(1)为防止汽车运行后电机传感器误差较大或者损坏,开发MCSRGHCKF电机转子转速和角度估计算法。在复杂的非高斯噪声环境下,仿真结果表明MCSRGHCKF算法对轮毂电机转速估计误差为0,除第6、9周期,角度估计误差为0。通过实验验证,MCSRGHCKF算法可跟踪4个电角度周期,误差约为-0.05 rad,转速估计误差为0.3 r/min,估计的数据精确可靠,滤波效果明显。
(2)设计积分滑模面,开发基于STSMC算法的转速和转矩控制器,并利用正弦过渡函数算法切换转矩。仿真结果表明,转速控制下,基于STSMC算法的转矩输出稳态误差为±6.7%,转速输出稳态误差为±0.002 5%,转矩模式下,转矩瞬时切换,输出稳态误差仅为±2.9%。实验验证,电机启动到匀速运行,STSMC算法下的转速超调量为6.33%,最大输出转矩为0.35 N·m,响应时间为0.22 s,稳态转速脉动为±0.5 r/min,转矩脉动为±0.01 N·m,控制精度高,响应快。直线加速时,转速切换转矩控制,转矩按照正弦函数快速平滑过渡,最大超调仅为2.86%,电机运行平稳。
[1] 关涛,刘大猛,何永勇.永磁轮毂电机技术发展综述[J].电工技术学报,2024,39(2):378-396.GUAN Tao, LIU Dameng, HE Yongyong. Review on development of permanent magnet in-wheel motors[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 378-396.(in Chinese)
[2] 章恒亮,花为.分布式驱动系统用轮毂电机及其技术综述[J].中国电机工程学报,2024,44(7):2871-2885.ZHANG Hengliang, HUA Wei. Overview of in-wheel traction machine and its key techniques for distributed-driving system[J]. Proceedings of the CSEE, 2024, 44(7): 2871-2885.(in Chinese)
[3] YANLING G, MOHAMED M. Speed control of direct current motor using ANFIS based hybrid PID configuration controller[J]. IEEE Access, 2020, 8: 125638-125647.
[4] ZHANG Xin, HONG Wenli, MENG Shao. Fixed-time-convergent sliding mode control with sliding mode observer for PMSM speed regulation[J]. Sensors, 2024, 24(5): 1561.
[5] 黄皓,涂群章,蒋成明,等.基于扰动观测器的农用驱动电机变速滑模控制[J].农业机械学报,2022,53(7):447-458. HUANG Hao, TU Qunzhang, JIANG Chengming, et al. Variable speed sliding mode control of agricultural drive motor based on disturbance observer[J]. Transactions of the Chinese Society for Agricultural Machinery, 2022,53(7): 447-458.(in Chinese)
[6] HUANG J, LIU S, ZHANG P, et al. Torque increase strategy for induction motor in the field-weakening region based on model predictive control[J]. Actuators, 2023, 12(10): 395.
[7] 李勇,胡晗,秦贞超,等.基于改进模型参考自适应的永磁轮毂电机无位置传感器控制[J].汽车安全与节能学报,2022,13(3):560-570. LI Yong, HU Han, QIN Zhenchao, et al. Sensorless control of permanent magnet in-wheel motor based on improved model reference adaptive strategy[J]. Journal of Automotive Safety and Energy, 2022, 13(3): 560-570.(in Chinese)
[8] 赵其进,廖自力,张运银,等.轮毂电机全速度范围无位置传感器控制研究[J].兵工学报,2019,40(5):915-926.ZHAO Qijin, LIAO Zili, ZHANG Yunyin, et al. Research on position sensorless control of hub motor in full speed range[J]. Acta Armamentarii, 2019, 40(5): 915-926.(in Chinese)
[9] 唐辉,殷德军,张楠,等.轮毂电机无位置传感器控制注入高频信号非线性分析与补偿[J].机械工程学报,2019,55(22):52-59.TANG Hui, YIN Dejun, ZHANG Nan, et al. Non-linear analysis and compensation of high-frequency signal injection based on sensorless in-wheel motor control[J]. Journal of Mechanical Engineering, 2019, 55(22): 52-59.(in Chinese)
[10] PASQUALOTTO D, RIGON S, ZIGLIOTTO M. Sensorless speed control of synchronous reluctance motor drives based on extended Kalman filter and neural magnetic model[J]. IEEE Transactions on Industrial Electronics, 2023, 70(2): 1321-1330.
[11] 宋战锋,毛丰羽,崔严谨,等.基于多级滞环控制器的表贴式双三相永磁同步电机低电流谐波直接转矩控制策略[J].中国电机工程学报,2023,43(11):4410-4422.SONG Zhanfeng, MAO Fengyu, CUI Yanjin, et al. Low current harmonic direct torque control strategy for surface-mounted dual-three-phase permanent magnet synchronous machine based on multi-level hysteresis controller[J]. Proceedings of the CSEE, 2023, 43(11): 4410-4421.(in Chinese)
[12] 郑长森,刘旭东.基于改进分数阶非奇异终端滑模方法的感应电机转速控制[J/OL].电气工程学报:1-9[2024-06-02]. http:∥kns.cnki.net/kcms/detail/10.1289.TM.20240308.1803.002.html.ZHENG Changsen, LIU Xudong. Speed control of induction motor based on improved fractional order non-singular terminal sliding mode method[J]. Journal of Electrical Engineering: 1-9[2024-06-02].http:∥knscnki.net/kcms/detail/10.1289.TM.20240308.1803.002.html.(in Chinese)
[13] 程启明,刘科,张昕,等.永磁同步电机的复叠式螺旋滑模控制策略研究[J].电机与控制学报,2023,27(6):116-126.CHENG Qiming, LIU Ke, ZHANG Xin, et al. Research on cascade spiral sliding mode control strategy of permanent magnet synchronous motor[J]. Electric Machines and Control, 2023, 27(6): 116-126.(in Chinese)
[14] KIM D J, KIM B. Linear matrix inequality-based robust model predictive speed control for a permanent magnetic synchronous motor with a disturbance observer[J]. Energies, 2024, 17(4): 869.
[15] 赵又群,林涛,林棻,等.基于ESO的机械弹性电动轮式车辆稳定性控制[J].吉林大学学报(工学版),2024,54(1):44-54.ZHAO Youqun, LIN Tao, LIN Fen, et al. Stability control of with mechanical elastic electric wheeled vehicles based on extended state observer[J]. Journal of Jilin University (Engineering and Technology Edition), 2024, 54(1): 44-54.(in Chinese)
[16] 赵治国,陈晓蓉,梁凯冲,等.考虑乘坐舒适性的纯电动公交车辆稳定性控制[J].机械工程学报,2023,59(10):250-262.ZHAO Zhiguo, CHEN Xiaorong, LIANG Kaichong, et al. Stability control method for the electric city bus considering riding comfort[J]. Journal of Mechanical Engineering, 2023, 59(10): 250-262.(in Chinese)
[17] 刘强,杨蔡进,张卫华,等.基于阿克曼原理的4WID/4WIS汽车循迹控制研究[J].动力学与控制学报,2023,21(1):36-44. LIU Qiang, YANG Caijin, ZHANG Weihua, et al. Research on tracking control of 4 WID/4 WIS vehicle based on Aekerman principle[J]. Journal of Dynamics and Control 2023, 21(1): 36-44.(in Chinese)
[18] 余志生.汽车理论[M].5版.北京:机械工业出版社,2009:22-24.
[19] 张征,马晓军,刘春光,等.基于分层模型的轮毂电机驱动车辆直接横摆力矩控制[J].农业机械学报,2019,50(12):387-394. ZHANG Zheng, MA Xiaojun, LIU Chunguang, et al. Direct yaw moment control based on hierarchical model for in-wheel motor drive vehicles[J]. Transactions of the Chinese Society for Agricultural Machinery, 2019, 50(12): 387-394.(in Chinese)
[20] 吴建洋,王震坡,张雷,等.四轮轮毂电机驱动电动汽车纵侧向稳定性协调控制策略研究[J].机械工程学报,2023,59(4):163-172. WU Jianyang, WANG Zhenpo, ZHANG Lei, et al. Coordination stability control strategy for four-wheel-independent-actuated electric vehicles[J]. Journal of Mechanical Engineering, 2023, 59(4): 163-172.(in Chinese)
[21] 黄亚东,郭桂芳.分布式驱动电动汽车转矩分配策略综述[J].汽车实用技术,2020,45(22):230-236,248.HUANG Yadong, GUO Guifang. A review of torque distribution strategies for distributed drive electric vehicles[J]. Automobile Applied Technology, 2020, 45(22): 230-236,248.(in Chinese)
[22] 袁雷,胡冰新,魏克银.现代永磁同步电机控制原理及MATLAB仿真[M].北京:北京航空航天大学出版社,2016:10-26.
[23] 李瑞,赵裔海,王俭朴.基于永磁同步电机的矢量控制和直接转矩控制策略研究[J].农业装备与车辆工程,2024,62(5):109-112.LI Rui, ZHAO Yihai, WANG Jianpu. Comparative study on vector control and direct torque control based on permanent magnet synchronous motor[J]. Agricultural Equipment &Vehicle Engineering, 2024, 62(5): 109-112.(in Chinese)
[24] 胡浩然,陈树新,吴昊,等.基于变分贝叶斯的连续-离散最大相关熵CKF算法[J].北京航空航天大学学报,2023,49(10):2859-2866.HU Haoran, CHEN Shuxin, WU Hao, et al. Continuous-discrete maximum correntropy CKF algorithm based on variational Bayes[J]. Journal of Beijing University of Aeronautics and Astronautics, 2023, 49(10): 2859-2866.(in Chinese)
[25] QUAN L, CHANG R, GUO C, et al. Vehicle state joint estimation based on lateral stiffness[J]. Sensors, 2023, 23(21): 8960.
[26] LIU D, CHEN X, XU Y, et al. Maximum correntropy generalized high-degree cubature Kalman filter with application to the attitude determination system of missile[J]. Aerospace Science and Technology, 2019, 95: 105441.
[27] 殷生晶,王晓琳.基于自适应超螺旋算法的高速永磁同步发电机稳压控制策略[J].电机与控制学报,2023,27(7):30-39.YIN Shengjing, WANG Xiaolin. Voltage-stabilizing control strategy of high-speed permanent magnet synchronous generator based on adaptive super-twisting algorithm[J]. Electric Machines and Control, 2023, 27(7): 30-39.(in Chinese)
