0 引言
近年来,离心泵已被广泛应用于工业、农业和城市供水等各个领域。然而,离心泵内空化的发生可能会显著影响泵性能、流动特性和稳定性。涡旋运动和分离流动是离心泵常见的流动现象,尤其是当离心泵发生空化时,伴随离心泵内空泡群的形成、发展和溃灭,叶轮流道内产生空化涡旋等不稳定流动[1-2]。离心泵内部不稳定流动产生的流体激励力及其自身振动会传递至其他机械设备,危害离心泵及其机组的安全运行[3]。因此,研究离心泵在空化条件下的内流特性和由于不稳定流动产生的压力脉动具有重要意义。
对空化流动不稳定性及其诱导的非定常动力特性研究吸引了大量学者。文献[4]对不同半高导叶叶片高度时离心泵内部流场进行非稳态数值分析,给出了导叶叶高对离心泵扬程曲线及压力脉动特性的影响。文献[5]研究了不同工况下混流泵内部压力脉动特性及其对流动诱导噪声的影响。研究发现混流泵叶轮进出口处的压力脉动幅值均是沿着轮缘到轮毂逐渐减小,叶轮进口处压力系数的最大值是出口处的2倍。文献[6]对超低比转数的离心泵IB50-32-250在不同空化数下的压力脉动进行研究,发现随着空化数降低,低频及宽频脉动信号增加,空化区边缘的脉动幅值增大。文献[7]研究了云状空化的动力学特性和声学特性,研究结果表明,空化云破裂形成的冲击波引发噪声并导致了材料破坏。文献[8]采用高速摄影和压力脉动测量技术系统分析了离心泵小流量工况下空化诱导的低频脉动特性。文献[9]研究了离心泵叶轮进口空化,初步获得了叶轮内不同空化程度下泵振动噪声特性的规律。文献[10]采用ZGB空化模型和FBDCM k-ε湍流模型模拟了Clark-Y水翼云空化绕流,利用涡量输运方程分析了空化与流体涡的相互作用,在三维情况下建立了上游水流卷吸能力与空化之间的关系。文献[11-13]采用涡量输运方程数值研究了绕水翼ALE15的空化-涡-湍流相互作用,并通过动态模态分解提取了相干结构。
近年来,随着涡动力学理论的发展,LIU等[14-17]提出的第三代涡识别方法——Omega涡识别方法在各类叶轮机械中得到了越来越多的应用。第三代方法能够定量化地表示涡的特性法,克服了传统涡识别方法需要针对具体流动调整阈值的问题,并能同时捕捉到强涡和弱涡。文献[18]通过对涡量法、Q准则法、λ2法、Rortex法等方法的比较,说明了不同方法在空化涡结构识别中的性能,结果表明Omega方法识别结果准确可靠。文献[19]基于Omega涡识别方法,对诱导轮内空化流动的流动结构及空化泡的关系进行研究。结果表明,Omega涡识别技术可以很好反映流动结构(剪切流与旋转流)与空化泡的关系。文献[20]对空化流场涡旋结构的形成机理及流动影响进行研究,发现新Omega涡方法捕捉到空腔内部的三维涡旋结构稳定,在临界空化条件下叶轮流道下游三维涡旋结构破碎且紊乱。文献[21]引入新Omega涡识别法,对液体火箭发动机涡轮氧泵流场中的涡结构进行了分析。结果表明,新Omega涡识别方法能够有效滤除流场中非旋转涡量部分,较好地捕捉流场中涡结构,可作为高速离心泵流场涡结构识别的首选方法。
目前,针对绕水翼空化关于空泡旋涡结构的试验研究已经比较完善,但离心泵空化研究的重点大多只局限于空泡的周期性脱落或者空化涡的结构演化特性,很少注意空化涡结构与周期性脱落空泡联合作用下的压力脉动特性。进一步分析离心泵空泡旋涡结构以及二者联合作用下对压力脉动影响,有利于进一步提高离心泵性能,为离心泵等水力机械设备不稳定流动机理研究提供参考。本文针对立式单级单吸蜗壳式离心泵在不同空化程度下叶轮区的内流特性及压力脉动特性进行数值模拟,结合涡动力学诊断涡旋结构与流动分离,探究空化对离心泵性能影响的机理,以期为进一步优化离心泵设计提供具体的参考与依据。
1 数值计算模型及方法
1.1 离心泵计算模型与网格划分
本文采用比转数ns为191.3的立式单级单吸蜗壳式离心泵作为研究对象,模型泵设计流量Qd为0.321 m3/s,设计扬程Hd为40.3 m,转速n为1 480 r/min,叶轮叶片数Z为7,所有工况均为纯水条件,不考虑来流含气。离心泵全流道计算流域包括进口弯肘型进水管、叶轮、蜗壳及出口扩散管4部分。采用三维建模软件UG NX进行几何建模,离心泵几何模型如图1所示。
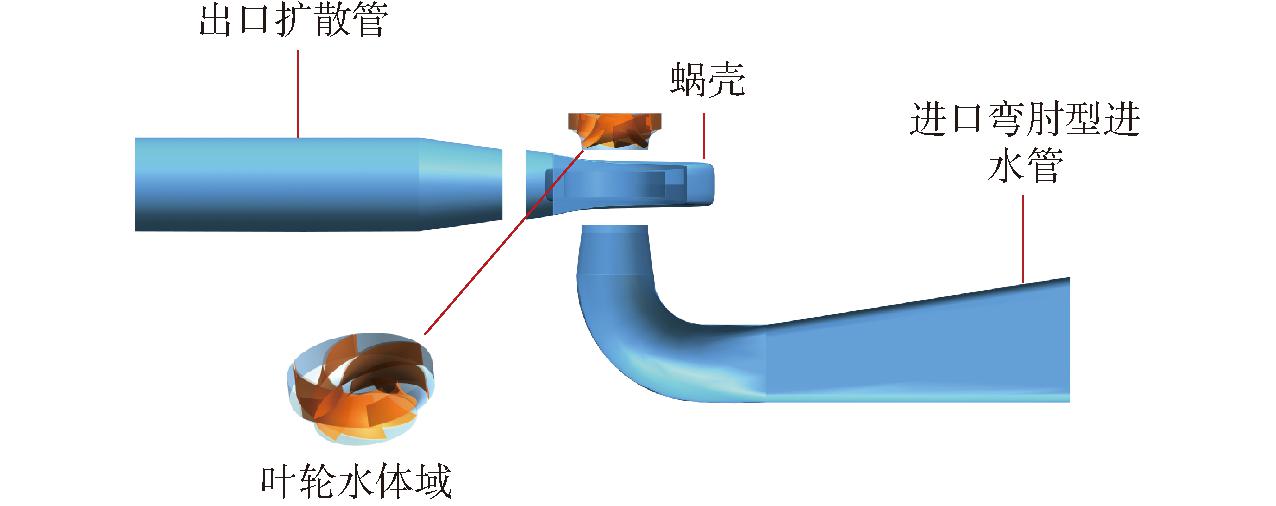
图1 离心泵水体模型
Fig.1 Computational domain of centrifugal pump
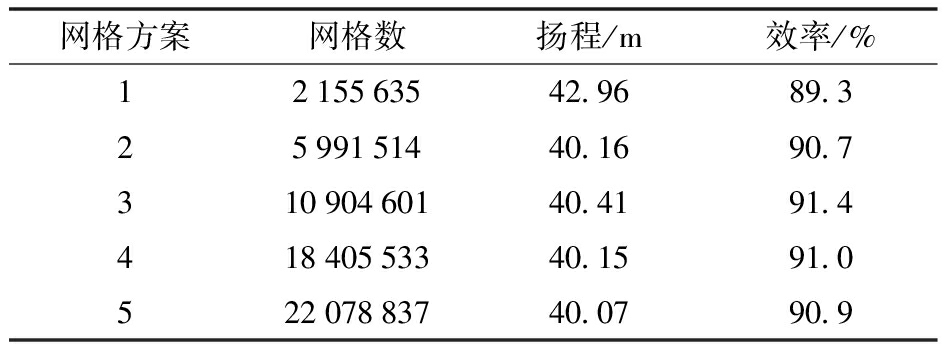
对各流域采用六面体结构网格进行划分,为了消除网格数量对数模结果精度的影响,进行网格无关性验证,如表1所示。综合考虑时间成本以及计算机配置,文中选用方案3进行后续计算,此时模型总网格数为10 904 601。所有部件网格质量均高于0.4,角度均大于18°。
表1 网格无关性分析
Tab.1 Grid independence analysis
网格方案网格数扬程/m效率/%1215563542.9689.32599151440.1690.731090460140.4191.441840553340.1591.052207883740.0790.9
1.2 数值计算方法
1.2.1 湍流模型
SST k-ω湍流模型在处理近壁面处低雷诺数计算上具有较高的精确度。由于考虑了流动过程湍流剪切力的传输,能够在逆压力梯度下准确预测流动分离,存在计算精度高和收敛性良好的优点。k-ω湍流模型假设湍流粘度与湍动能和湍流频率相关,用来求解湍动能k和耗散率ω,关系式为
(1)
![]()
Gk-β*ρkω
(2)
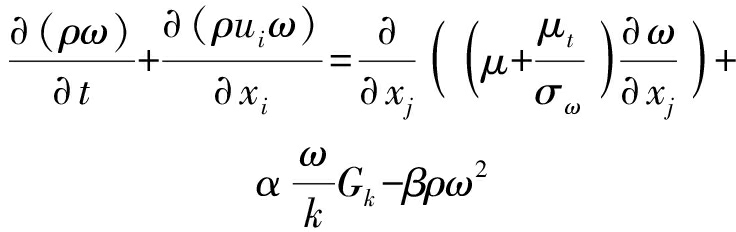
(3)
式中 ρ——流体密度
β——辅助参数 ui——速度
β*——辅助参数临界值
Gk——湍流产生项
σk——湍流动能耗散率
σω——湍流涡度耗散率
μ——动态黏度
μt——湍流黏度
α——热扩散系数
1.2.2 空化模型
Schnerr-Sauer空化模型由文献[22]提出,用来求解空化相变过程。Schnerr-Sauer空化模型基于Rayleigh-Plesset单气泡动力学方程,通过联立混合相连续方程与气相体积分数方程,得到气相质量变化率与气相体积分数变化率之间的关系,蒸发项m+和凝结项m-计算公式分别为
![]() (P<Pv)
(P<Pv)
(4)
![]() (P≥Pv)
(P≥Pv)
(5)
其中
(6)
式中 ρl——液相密度 ρv——气相密度
Pv——饱和蒸汽压力
P——流场局部压力
Cv——凝结系数 Cc——蒸发系数
RB——空泡半径
n0——空泡数密度
αv——气相体积分数
1.2.3 边界条件设置
采用ANSYS-Fluent软件对离心泵内流三维黏性流动进行非定常计算,非定常计算均使用定常计算结果作为初始场。采用压力进口,质量流量出口为边界条件,壁面选择无滑移壁面;近壁区采用标准壁面函数。残差收敛精度设置为10-6。计算时设置叶轮旋转6圈,时间步长设为3×10-4 s,即每旋转3°计算1次,总时长为0.25 s。为保证计算精度及稳定性,取后4圈的计算结果进行分析。
2 数值模拟结果与分析
2.1 离心泵能量特性分析
为了保证数值模拟结果的准确性,对模型泵扬程和效率计算结果与试验结果比较,试验数据来自中国水利水电科学研究院水力机械实验室TP3试验台。如图2所示,最高效率点出现在1.1~1.2倍设计工况附近,水力效率为92.1%~92.9%,模型泵扬程和效率的变化趋势与试验数据相同,误差较小。如图3所示,空化性能数值预测与模型试验空化性能曲线二者效率变化趋势相同,误差较小。由此可知,本文采用的数值计算模型以及数值计算方法具有较高的可靠性。

图2 离心泵数值计算与试验外特性曲线对比
Fig.2 Comparison between numerical and experimental external characteristic curves of pump
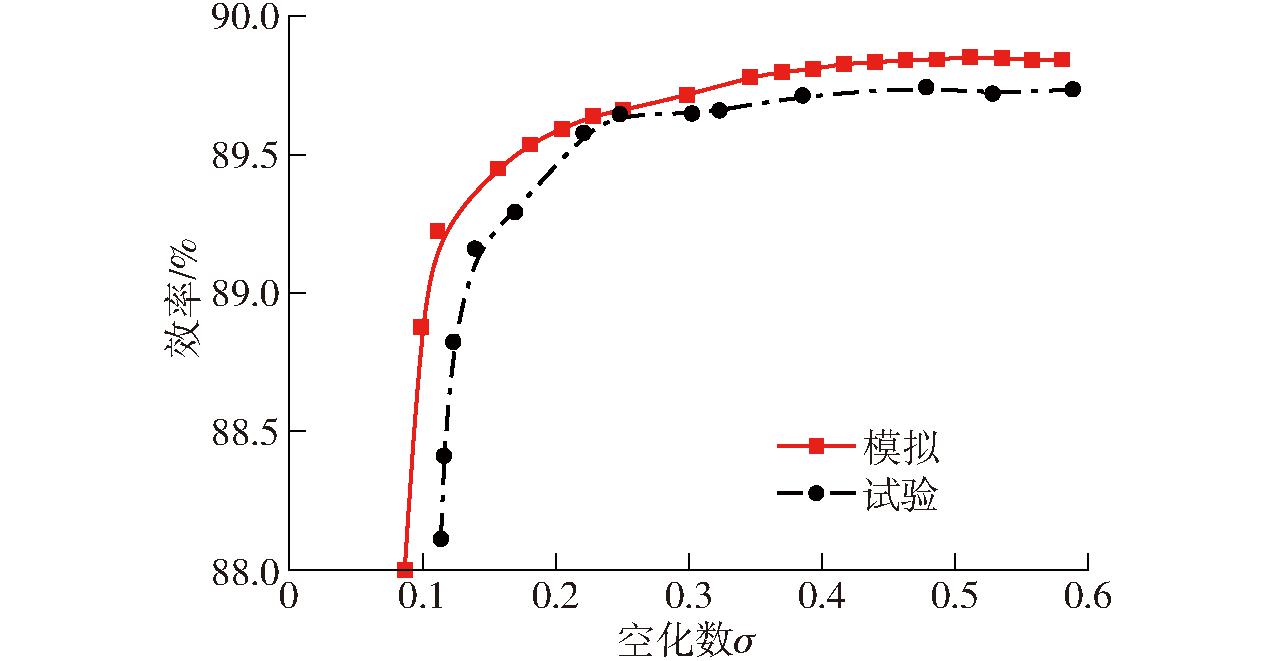
图3 离心泵数值计算与试验空化特性曲线对比
Fig.3 Comparison between numerical and experimental cavitation characteristic curves of pump
2.2 空化对叶轮不同位置处压力脉动特性的影响
2.2.1 压力脉动监测点选取
为了更全面对空化下叶轮流域的压力脉动变化进行分析,沿着叶片骨线在叶片工作面及背面各设置5个监测点。如图4所示,叶轮叶片压力面监测点从进口到出口依次为P1、P2、P3、P4和P5,叶片吸力面从进口到出口为S1、S2、S3、S4和S5。
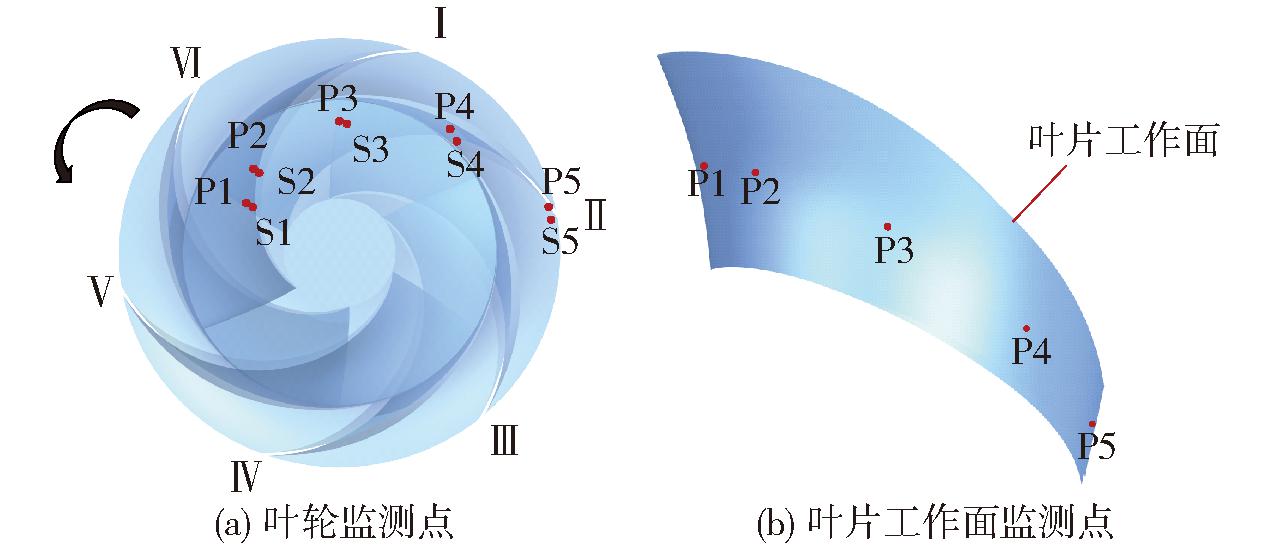
图4 压力脉动监测点位置
Fig.4 Location of monitoring points
2.2.2 压力脉动频域分析
图5为设计工况Qd下叶轮监测点在不同空化程度下的频域图。对旋转频率进行无量纲化,f为监测点频率,转频fd=1 480/60=24.67 Hz,叶频fp为6倍转频,为148 Hz。根据图5可知,在各个空化程度下,叶轮内各监测点的压力脉动的主要峰值信号为叶轮转频及其倍频,频谱中叶频的幅值远大于其他频率信号,为叶轮旋转过程中的主要频率。从进口到出口压力脉动的幅值逐渐增大,在同一半径上吸力面的压力脉动幅值小于压力面的脉动幅值。随着空化数的减小,由于空泡占据叶轮流道,流场连续性被破坏,流体做功能力被削弱,压力脉动幅值整体呈减小趋势。压力面进口处主频幅值随着空化数的降低先增后减,最后达到临界点时呈爆炸式增长。当空化数σ为0.086时P1监测点处压力脉动达到最大值53 kPa。当空化数σ从0.219降低至0.095时,离心泵叶轮叶片上的空泡团具有可压缩性,能够吸收一部分由于空泡破灭产生的能量,当空化数σ继续降低到临界空化点时,此时的空泡团不再具有可压缩性,离心泵压力振动能量由于空泡溃灭释放的能量呈爆炸式增长。恶劣空化工况下,叶轮出口处流场受空泡脱落的影响产生涡旋,涡团的形成、脱落造成了叶轮出口处压力脉动的迅速增大。当空化数σ等于0.095时,压力面监测点P1、P2和吸力面监测点S1、S2压力脉动幅值降低到接近零,是由于此时叶片附着空泡完全覆盖监测点;同时,由于受到空泡脱落的影响,监测点P3、P4、S3、S4低频压力脉动信号增加。当空化数σ继续降低到0.086,离心泵达到临界空化点时,监测点P3、P4、S3、S4压力脉动幅值也降低到接近零,此时空泡已经没过监测点S4处,流道被空泡占据。
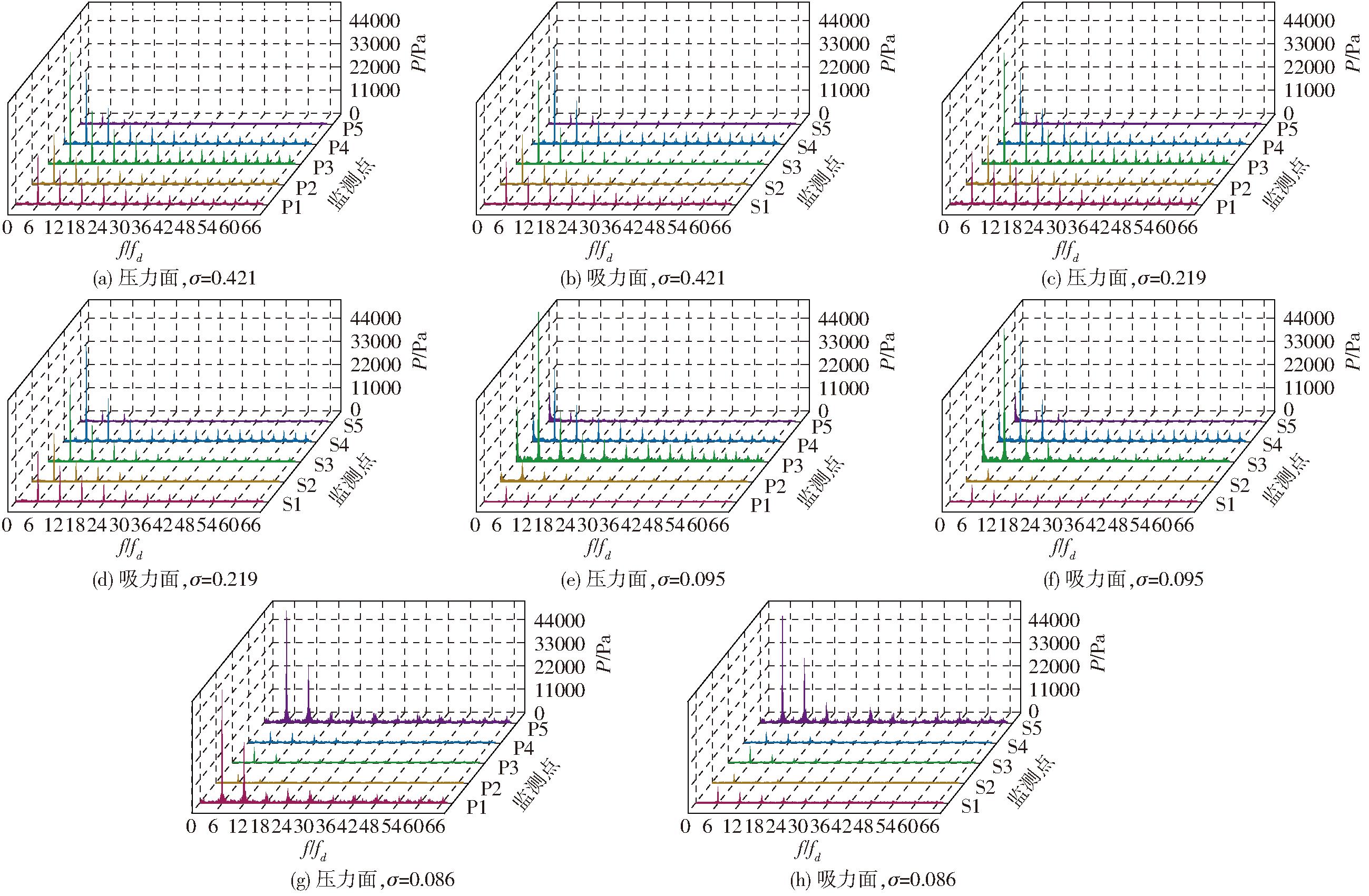
图5 不同工况下叶片监测点压力脉动频域
Fig.5 Frequency domain of pressure pulsation at blade monitoring points under different working conditions
2.2.3 压力脉动幅值分析
图6为叶轮进口检测点P1叶频压力与离心泵扬程随空化数变化图。随着空化数的降低,离心泵内空化逐渐加剧,当空化数降低到临界空化数σc(0.086)时,离心泵扬程发生断崖式骤降。结合空化诱导压力脉动能量特性,将离心泵的空化分为空化初始阶段(阶段Ⅰ:σ为0.622~0.270)、空化发展阶段(阶段Ⅱ:σ为0.270~0.169)、空化状态转变阶段(阶段Ⅲ:σ为0.169~0.086)、空化恶化阶段(阶段Ⅳ:σ≤0.086)4个阶段。

图6 依据空化诱导压力脉动划分的空化演变阶段
Fig.6 Cavitation evolution stages divided according to cavity-induced pressure pulsations
2.3 不同空化工况下叶轮内流场分析
2.3.1 内部流动分析
空化的发展伴随着空泡的初生、发展、溃灭的过程,空泡的变化直接影响离心泵内流场压力。图7和图8分别为设计工况Qd不同阶段下叶轮中间截面总压和空泡体积分数为10%的等值面图。
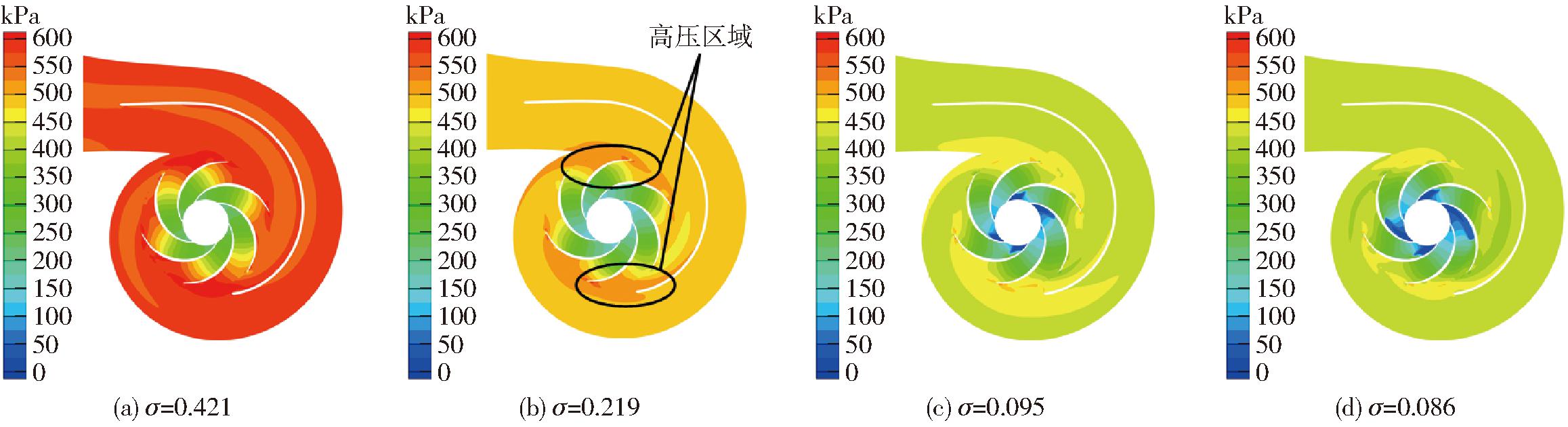
图7 不同空化程度叶轮中间截面总压
Fig.7 Total pressure in middle section of impeller with different cavitation degrees

图8 不同工况下气泡体积分布
Fig.8 Bubble volume distributions under different working conditions
当空化数降低到初生空化点时,叶轮进口吸力面附近开始产生空泡,随着空化数的降低,空泡沿着叶片低压区逐渐向叶轮出口以及叶片压力面延伸扩展,并伴随着叶轮进口气蚀环的出现,气蚀环是由气液混合形成的明显气泡环,扰动了泵内的流体流动状态,减小了有效的液体填充率,导致液体流动受到阻碍和扰动,形成了不稳定的流场结构。在4种不同的空化阶段中,Ⅰ、Ⅳ号叶片上空泡面积均小于其他叶片。这是由于受到隔舌高压区域以及高压力梯度的影响,Ⅰ、Ⅳ号叶片流道已经产生了比较大的旋涡,导致空泡无法生成。随着空化数减小,离心泵进口压力降低,隔舌附近的高压区以及高压力梯度区面积明显降低,气泡迅速占领流道。
当空化数σ降低到0.095时,空泡团尾端与叶片分离,此时空泡将随着叶轮旋转从主空泡团上脱落,进入叶轮流道撞击叶片,向叶轮下游高压区移动。脱落的空泡团随着环境压力的变化将完成缩小、增大、溃灭的过程。此时离心泵的能量处于一个下降过程,由经典的空化理论可知,此时空泡区域具有可压缩性,能够吸收一部分由于空泡破灭产生的能量,进而削弱由于空化产生的激励力[23]。当空化数σ降低到0.086时,空泡已经发展到叶轮流道,且此时空泡区域不再具有可压缩性,空泡在叶轮流道内溃灭,导致离心泵的振动能量迅速上升,伴随离心泵扬程发生断崖式骤降。这是叶轮区压力脉动靠近叶轮出口处监测点压力脉动发生突变的主要原因。
2.3.2 内部涡量结构分析
离心泵内部发生空化时,叶轮内部的流场流速和压力分布会受到空化涡影响,从而导致流线和压力的紊乱。研究离心泵内的涡流结构和涡量变化,有助于进一步了解空化诱导的压力脉动变化的根本原因。本文采用Q准则和Omega方法研究空化下离心泵内部大尺度流动结构与空泡的相互关系。Q准则和Omega方法均是基于对速度梯度张量![]() 的分解。
的分解。![]() 可以被分解为两部分,即一个对称张量A和一个反对称张量B,分别表示流场中某一点的变形和旋转。Omega方法[14-17]将流体微团的涡量进一步划分为旋转部分和非旋转部分,即涡量可表示为
可以被分解为两部分,即一个对称张量A和一个反对称张量B,分别表示流场中某一点的变形和旋转。Omega方法[14-17]将流体微团的涡量进一步划分为旋转部分和非旋转部分,即涡量可表示为
ω=R+S
(7)
式中 R——旋转部分涡量
S——非旋转(即纯剪切)部分涡量
通常而言,R和S方向不同。引入一个参数Ω,表示旋转部分涡量占总涡量的比例。Omega涡识别法公式为
(8)
Q准则基于速度梯度张量的第二矩阵不变量[24],其表达式为
(9)
其中
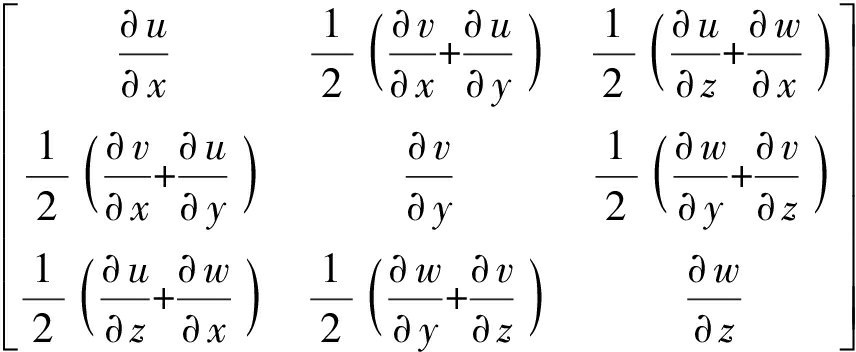
(10)
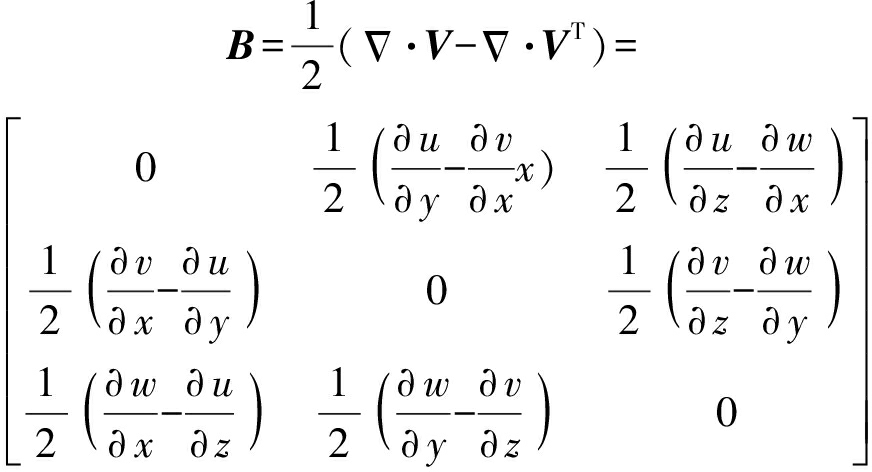
(11)
式中,ε为一个正数,其目的是为了避免分母为0;u、v、w表示x、y、z方向上的速度分量;‖·‖F表示矩阵的Frobenius范数。当流体旋转作用超过剪切作用时,认为是旋涡。
对于Q准则判别法,Q>0表示在流动中流体的旋转占主导地位,Q准则对阈值的选取非常敏感,Q越大则表明流体在该处的旋转率越大,存在旋涡的可能性也越大,阈值对识别出来的涡旋影响很大。
对于Omega判别法,Ω表示流动中旋转与剪切作用的占比,通常可以取固定值(Ω=0.52)来表示旋涡边界。Omega涡识别技术最显著的优点是它可以同时捕捉流场中强涡和弱涡,不受阈值的影响。
图9和图10分别为设计流量Qd下不同空化数下叶轮内Ω=0.52的涡旋结构分布图和涡旋Q等值面图。通过取高Q值(Q=70 000 s-2)等值面,得到离心泵叶轮流域内高旋度区域,以此判断涡核中心。
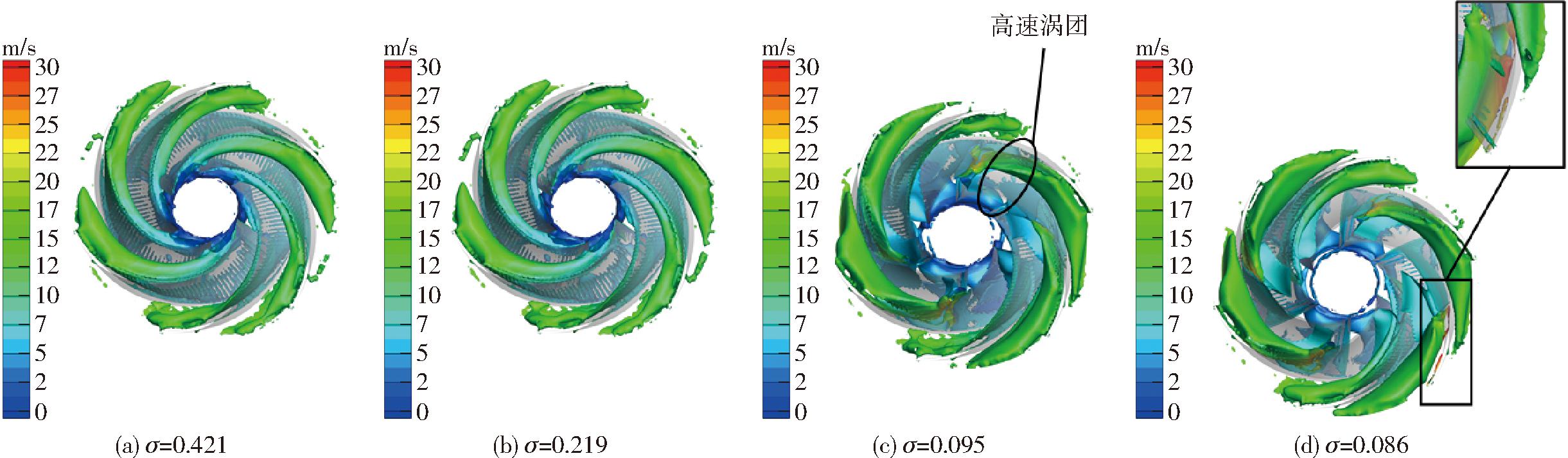
图9 不同工况下旋涡结构分布(Ω=0.52)
Fig.9 Vortex structure distributions under different working conditions (Ω=0.52)
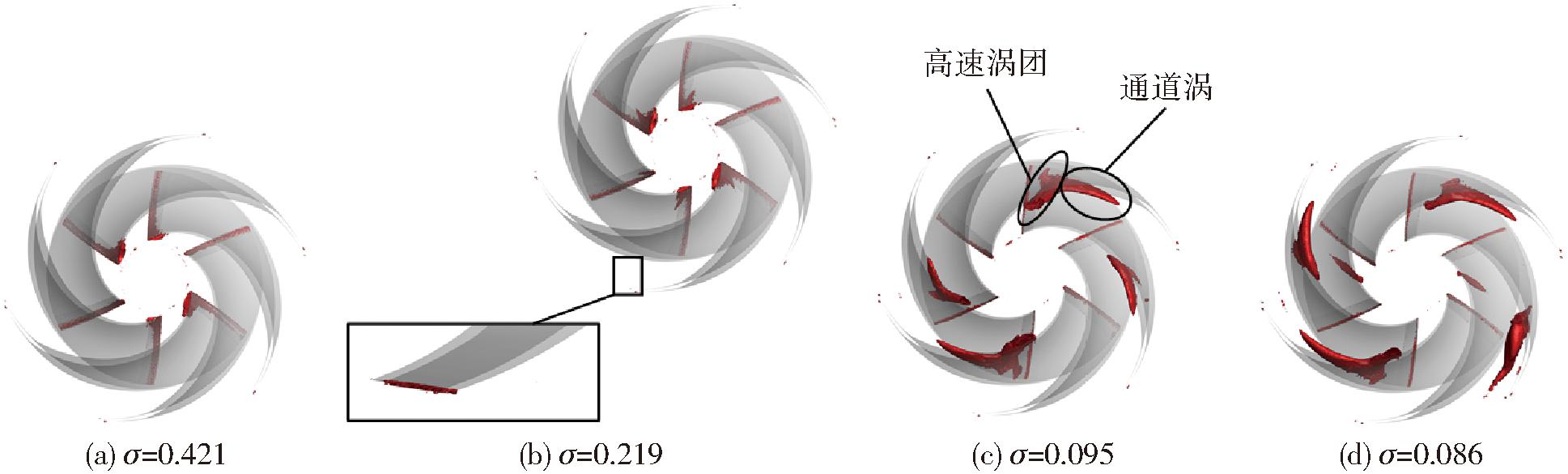
图10 不同工况下涡旋结构分布(Q=70 000 s-2)
Fig.10 Vortex structure distributions under different working conditions (Q=70 000 s-2)
在空化发生初期,受空泡初生的影响,在叶片进口处吸力面位置产生涡,该涡位置与叶片空泡位置相同;同时,在各个空化阶段叶轮出口均有微小的涡团,该涡团是由叶片出口处局部高压区和逆压引起的。叶片尾部几何形状导致中截面流场点状高压区形成。Omega方法可以清晰地捕捉到叶轮进口的回流涡、叶轮流道内通道涡和叶轮尾缘处的尾迹涡。随着空化的发展,叶轮通道内的强涡区域开始扩大,通道涡的旋转强度逐渐增大并向叶轮出口处转移。同时,在空泡下游处出现了速度大于30 m/s的高旋转强度的高速涡团,高速涡团的形成是由于空泡脱落和气液混合导致的流动不稳定性。局部的气液流动可能产生剧烈的流体扰动、速度扰动,从而形成速度较大的涡团。气液混合的高速涡团随着叶轮的转动向叶轮下游高压区移动,高速涡团快速的形成、脱落导致离心泵内压力快速振荡,压力脉动幅值升高,威胁离心泵的安全稳定运行。
3 结论
(1)离心泵内不同空化程度下各监测点的主频均为叶频。空化发展过程中,受空泡脱落、覆盖的影响,叶片中间6个监测点经历低频脉动信号增加到整体压力脉动信号骤降到接近零的过程;叶片进口监测点由于空泡形态变化经历先增后减再增过程;叶片出口监测点由于空泡溃灭在空化严重时压力脉动能量呈爆炸式增长,当空化数σ为0.086时,P1监测点处压力脉动达到最大值53 kPa。
(2)在空化发生的前几个阶段,受到隔舌高压区域以及高压力梯度的影响,流道内出现了大面积旋涡,阻碍空泡的生成,导致离心泵内叶片空泡呈对称分布且大小不同;空化严重时,空泡团尾端与叶片分离,并随着叶轮旋转发生脱落,进入下游高压区完成缩小、增大、溃灭的过程。
(3)Omega方法不受阈值的影响,可以有效识别离心泵空化状态下不同结构形式的强涡、弱涡。在空化初生阶段,离心泵内存在叶轮进口的回流涡、叶轮流道内通道涡和叶轮尾缘处的尾迹涡;随着空化的发展,受到空泡脱落的影响以及局部气液流动导致的流体扰动,在主空泡团下端位置出现速度大于30 m/s高速涡团,其形成、脱落是离心泵压力脉动振荡的原因。
[1] 叶晓琰,王朋,张德胜,等.不同叶片后掠角度下轴流泵叶顶区空化流场与性能研究[J].农业机械学报,2022,53(10):194-201.YE Xiaoyan, WANG Peng, ZHANG Desheng, et al. Cavitation flow field in tip region and performance of axial flow pump under different blade swept angles[J]. Transactions of the Chinese Society for Agricultural Machinery,2022,53(10):194-201.(in Chinese)
[2] LUO X, JI B, TSUJIMOTO Y. A review of cavitation in hydraulic machinery[J]. Journal of Hydrodynamics, 2016, 28(3): 335-358.
[3] 袁寿其,施卫东,刘厚林,等.泵理论与技术[M].北京:机械工业出版社,2014.
[4] 江伟,朱相源,田辉,等.半高导叶对离心泵压力脉动影响的数值模拟与试验研究[J].中南大学学报(自然科学版),2021, 52(4): 1276-1286.JIANG Wei,ZHU Xiangyuan,TIAN Hui, et al. Numerical and experimental study of influence of semi-high guide vane on pressure fluctuation in centrifugal pump[J].Journal of Central South University (Science and Technology),2021, 52(4): 1276-1286. (in Chinese)
[5] 郑源,陈宇杰,毛秀丽,等.混流泵压力脉动特性及其对流动诱导噪声的影响[J].农业工程学报,2015,31(23): 67-73.ZHENG Yuan,CHEN Yujie, MAO Xiuli, et al. Pressure pulsation characteristics and its impact on flow-induced noise in mixed-flow pump[J]. Transactions of the CSAE, 2015, 31(23): 67-73. (in Chinese)
[6] 王聪,张永学,冀凯卓,等.空化对超低比转数离心泵内压力脉动的影响研究[J].农业机械学报,2020,51(1): 122-129.WANG Cong, ZHANG Yongxue, JI Kaizhuo, et al. Investigation on pressure fluctuation affected by cavitation in ultra-low specific speed centrifugal pump[J]. Transactions of the Chinese Society for Agricultural Machinery,2020,51(1): 122-129.(in Chinese)
[7] REISMAN G E, WANG Y C, BRENNEN C E. Observations of shock waves in cloud cavitation[J]. Journal of Fluid Mechanics, 1998, 355: 255-283.
[8] FU Y X, YUAN J P, YUAN S Q, et al. Numerical and experimental analysis of flow phenomena in a centrifugal pump operating under low flow rates[J]. Journal of Fluids Engineering, 2015, 137(1): 011102.
[9] 王勇,刘厚林,袁寿其,等.离心泵非设计工况空化振动噪声的试验测试[J].农业工程学报,2012,28(2):35-38.WANG Yong, LIU Houlin, YUAN Shouqi, et al. Experimental testing on cavitation vibration and noise of centrifugal pumps under off-design conditions[J]. Transactions of the CSAE, 2012, 28(2): 35-38. (in Chinese)
[10] LONG X, CHENG H, JI B, et al. Numerical investigation of attached cavitation shedding dynamics around the Clark-Y hydrofoil with the FBDCM and an integral method[J]. Ocean Engineering,2017, 137: 247-261.
[11] LIU M, TAN L, LIU Y, et al. Large eddy simulation of cavitation vortex interaction and pressure fluctuation around hydrofoil ALE 15[J]. Ocean Engineering,2018,163: 264-274.
[12] LIU M, TAN L,CAO S.Cavitation-vortex-turbulence interaction and one-dimensional model prediction of pressure for hydrofoil ALE15 by large eddy simulation[J].ASME J. Fluids Eng.,2019,141(2): 21103.
[13] LIU M, TAN L, CAO S. Dynamic mode decomposition of cavitating flow around ALE 15 hydrofoil[J]. Renewable Energy,2019, 139: 214-227.
[14] LIU Chaoqun, GAO Yisheng, TIAN Shuling, et al. Rortex: a new vortex vector definition and vorticity tensor and vector decompositions[J].Physics of Fluids,2018,30(3): 035103.
[15] 刘超群.Liutex—涡定义和第三代涡识别方法[J].空气动力学学报,2020,38(3):413-431,478.LIU Chaoqun. Liutex: vortex definition and third generation vortex identification method[J].Journal of Aerodynamics,2020,38(3): 413-431,478. (in Chinese)
[16] LIU Chaoqun, WANG Yiqian, YANG Yong, et al. New Omega vortex identification method[J]. Science China (Physics,Mechanics,Astronomy),2016,59(8): 684711.
[17] GAO Yisheng, LIU Chaoqun. Rortex and comparison with eigenvalue-based vortex identification criteria[J].Physics of Fluids,2018,30(8): 085107.
[18] WANG C C, LIU Y, CHEN J, et al. Cavitation vortex dynamics of unsteady sheet/cloud cavitating flows with shock wave using different vortex identification methods[J]. Journal of Hydrodynamics, 2019, 31(3): 475-494.
[19] 闫龙龙,高波,张宁,等.基于Omega涡识别方法的诱导轮内非定常空化流动分析[J].工程热物理学报,2023,44(3):654-659.YAN Longlong, GAO Bo, ZHANG Ning, et al.Analysis of unsteady cavitating flow in an inducer based on Omega vortex identification[J]. Journal of Engineering Thermophysics, 2019,44(3):654-659. (in Chinese)
[20] 伍杰,邱宁,朱涵,等.基于非定常空化流动的离心泵涡旋结构数值分析[J].西华大学学报(自然科学版),2023,42(1):90-99.WU Jie, QIU Ning, ZHU Han, et al. Numerical analysis of vortex structure in centrifugal pump based on unsteady cavitation flow[J]. Journal of Xihua University (Natural Science Edition),2023,42(1):90-99. (in Chinese)
[21] 杨宝锋,李斌,陈晖,等.新Omega涡识别法在液体火箭发动机涡轮氧泵中的应用[J].推进技术,2019,40(9):2105-2112.YANG Baofeng, LI Bin, CHEN Hui, et al. Application of new Omega vortex identification method in liquid rocket engine oxygen pump[J]. Journal of Propulsion,2019,40(9):2105-2112. (in Chinese)
[22] SCHNERR G H, SAUER J. Physical and numerical modeling of unsteady cavitation dynamics[C]∥The 4th International Conference on Multiphase Flow, New Orleans, 2001.
[23] KUIPER G. Cavitation in ship propulsion[M]. Springer,2008.
[24] HUNT J,WRAY A,MOIN P. Eddies, stream, and convergence zones in turbulent flows[R]. Center for Turbulent Research Report CTR-S88,1988:193-208.